О ПРИМЕНИМОСТИ ПРИНЦИПА "ЭФФЕКТИВНОЙ ВЫСОТЫ" ПРИ РАСЧЕТЕ

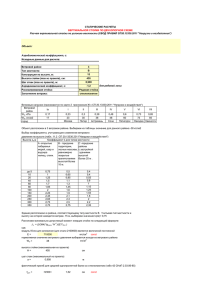
О ПРИМЕНИМОСТИ ПРИНЦИПА
"ЭФФЕКТИВНОЙ ВЫСОТЫ" ПРИ РАСЧЕТЕ
ВЕТРОВЫХ ВОЗДЕЙСТВИЙ НА ВЫСОКИЕ
ЗДАНИЯ
А.С. Кубенин
Аннотация
Рассмотрена методика расчета средней составляющей ветровой нагрузки на фасады высоких зданий
в актуализированной редакции СНиП 2.01.07-85*. Обсуждается способ нахождения распределений ветрового давления на фасадах сложной конфигурации, сочетающий методы физического и численного моделирования обтекания здания.
Введение
Находясь в ветровом потоке, высотное здание
испытывает аэродинамические нагрузки, которые
складываются, главным образом, из распределений
давления по его фасадам (напряжения трения сравнительно малы). Принято считать, что с увеличением
высоты ветровая нагрузка на здание возрастает пропорционально увеличению скоростного напора настилающего ветра с высотой [1-2]. Однако это представление справедливо лишь для наветренных фасадов отдельно стоящего здания. Изменение собственных горизонтальных планов здания, наличие выступающих
декоративных элементов, близость к покрытию, а
также наличие соседних высоких объектов – всё это
оказывают существенное влияние на распределения
ветрового давления по фасадам. Необходимая дополнительная информация о ветровых нагрузках на высокие сооружения сложной конфигурации может быть
получена с помощью методов физического (в аэродинамических трубах) или математического (компьютерного) моделирования.
В работе представлены примеры трехмерного
компьютерного моделирования обтекания комплекса
зданий турбулентным воздушным потоком и результаты верификации применяемой компьютерной технологии. Так же в работе приводится пример расчета
средней составляющей ветровой по методике СНиП
[2] с априорным заданием коэффициента давления.
На основе сравнения результатов компьютерного моделирования и расчета по инженерной методике дается уточнение понятия «эффективная высота»,
составляющего основное нововведение в разделе ветровые нагрузки актуализированной редакции СНиП
[2].
Определение расчетной ветровой нагрузки wm
В соответствии с методическими требованиями СНиП [2] расчетные значения средней ветровой
нагрузки на единицу площади фасада здания определяются по формуле:
(1)
wm = w0 k ( z ) c γ ,
где w0 – нормативное значение ветрового давления,
зависящее от ветрового района, Па; k = f(z) – коэффициент возрастания ветрового напора с высотой z, зависящий от типа местности A, B или C в соответствии
с нормативными табличными данными; c – аэродинамический коэффициент давления; γ – коэффициент
надежности по ветровой нагрузке (принимается равным 1.4).
В отличие от исходной, в новой актуализированной редакции СНиП в формуле (1) вместо фактической высоты z рекомендуется применять эквивалентную высоту ze, которая для высоких зданий при
h > 2d (h – высота, d – характерный поперечный размер здания) определяется как
⎧h , z > h − d ;
⎪
(2)
ze ( z ) = ⎨ z , d < z < h − d ;
⎪d , 0 < z < d .
⎩
Формула (1) пригодна для оценок ветровой
нагрузки лишь в простейших стандартных случаях,
когда аэродинамический коэффициент c – заранее известен. Например, для срединной части наветренной
стороны открытого фасада здания c ≈ 1 c хорошей
точностью. Однако в общем случае формула (1) не дает правильного представления о величине ветровой
нагрузки, поскольку входящий в неё аэродинамический коэффициент c суть неизвестная переменная величина. Рекомендация [2] на этот случай – использовать результаты продувок моделей в аэродинамических трубах.
Технология трехмерного компьютерного моделирования и её верификация
Трехмерная конфигурация тел 1обтекается турбулентным потоком несжимаемой воздушной среды,
имеющим распределение средней скорости по высоте
расчетной области согласно трехпараметрическому
степенному закону
α
⎛ z ⎞
U ( z ) = U 0 ⎜ ⎟
⎝ z0 ⎠
(3)
типа местности, в частности, при z0 =30.5 м/с и α =0.2
зависимость k(z) полностью соответствует нормативной зависимости коэффициента высоты по СНиП [2]
для типа местности «B», [3]. Расчет выполнен для
первого ветрового района (U0 =19.2 м/с) и типа местности «B» согласно своду правил [2].
Турбулентное движение воздушной среды около здания описывается системой уравнений Рейнольдса, замыкаемых с помощью дополнительных дифференциальных соотношений двухпараметрической диссипативной модели турбулентности, используется вычислительная технология RANS/URANS, основанная
на методе контрольного объёма [4-6]. Рассчитывается
картина обтекания и распределение давления на фасадах здания. Используемый коммерческий код –
ANSYS Fluent 14.5.
С целью верификации применяемой вычислительной технологии были выполнены тестовые расчеты обтекания модельной конфигурации строительного
комплекса, испытывающегося в аэродинамической
трубе НИИ механики МГУ, рис.1. На рис. 2 представлено сравнение результатов расчета и эксперимента
по определению аэродинамического коэффициента на
периметре горизонтального сечения (на высоте 0.6 h)
одного из высоких элементов модельного комплекса.
где U0 – средняя скорость ветрового потока на высоте
z0. Соответствующее распределению (3) выражение
для коэффициента высоты k(z) в формуле (1) имеет
вид k = (z / z0)2α. Значения параметров z0 и α зависят от
1
Высота каждой секции макета h=0.25 м, в поперечном сечении
секции почти окружность d=0.066 м. Секции идентичны между
собой. Макет физического эксперимента (рис. 1) полностью соответствует макету вычислительного эксперимента (рис. 2, 3).
Рис. 1 Макет 3-х секционного комплекса на столе
аэродинамической трубы А10 НИИ механики МГУ
.
Рис. 2 Сравнение физического и численного экспериментов
Рис. 3 Распределение ветрового давления
наветренной стороне фасадов комплекса зданий
на
Результаты расчетов
Сложная конфигурация здания, содержащего
близко расположенные 3-х секций комплекса приводит к образованию многочисленных отрывных и
струйно-вихревых зон (рис. 2, направление ветра указано стрелкой), которые, взаимодействуя между собой,
формируют немонотонные распределения ветрового
давления на фасадах здания (рис. 3).
Рис. 4 Распределение ветрового давления по высоте
центральной секции комплекса на наветренной стороне (лобовая линия)
Рис. 2 Векторное поле скорости в горизонтальном
сечении на высоте z = 68 м над уровнем земли
Заключение
Сравнение по распределению ветрового давления по высоте центральной секции жилого комплекса
(вдоль лобовой линии), полученного или средствами
компьютерного моделирования, или с использованием
формулы (1) с априорным заданием коэффициента
давления c p = 1, дает основу заключить, что появление понятия эквивалентной высоты в актуализированной версии СНиП 2.01.07-85* было призвано учесть
концевые эффекты в окрестности покрытия и основания здания. Видно, что кривая удельной ветровой
нагрузки, полученная по новой версии СНиПа, в месте
основания здания приближена к данным вычислительного эксперимента, который в нашем случае является эталоном. Однако же на удалении поперечного
размера от покрытия (по направлению к земле) инженерная формула дает завышенное значение ветровой
нагрузки, что, по всей видимости, можно обосновать
вкравшейся неточностью в свод правил [2]. Скорее
всего, для случая z > h − d
эквивалентная высота должна быть z E = h − d , а не
z E = h , как в системе (2).
Очевидно, что введение принципа эквивалентной высоты дает преимущества в одном единственном
случае, когда нужно определить ветровую нагрузку на
одиночном сооружении стандартной конфигурации,
(см. приложение СП [2]) когда аэродинамические коэффициенты априорно известны.
Во всех других случаях, когда аэродинамические коэффициенты берутся из результатов физического или численного экспериментов, формула (1) с
нахождением z, исходя из системы (2), не применима,
так как концевые эффекты и так будут учтены автоматически.
Полностью не применима формула (1) для случая, когда на стадии эксперимента моделируется помимо исследуемого объекта прилегающая застройка,
что ведет к искажению настилающего потока вблизи
исследуемого объекта, и поэтому уже нельзя восста-
новить ветровое давление по аэродинамическим коэффициентам, полагая, что настилающий сдвиговый
поток остается невозмущенным. В этом случае ветровое давление нужно непосредственно получать из эксперимента.
При всем вышеописанном не утрачивают своего значения нормативы, закрепленные в СНиП для задания параметров ветровых потоков для различных
ветровых районов и типов местности, которые полезны в качестве граничных условий.
Список литературы.
1. Табунщиков Ю.А., Шилкин Н.В. Аэродинамика высотных зданий // AВОК. 2004. №8.
2. Строительные нормы и правила. Нагрузки и
воздействия. СНиП 2.01.07-85.–М.: Госстрой. 1986. –
36 с. + Свод правил СП 20.13330.2011/ Актуализированная редакция СНиП 2.01.07-85* «Нагрузки и воздействия». – М: ОАО «ЦПП», 2011. – 85 с.
3. Гагарин В.Г., Гувернюк С.В. Компьютерное
моделирование ветровой нагрузки на элементы фасадов зданий для развития методики СНиП 2.01.07-85
"Нагрузки и воздействия". // Фасадные системы. 2007.
№1. стр. 30-36.
4. ANSYS FLUENT 14.5 Documentation
5. В.Г. Гагарин, С.В. Гувернюк, П.В. Леденев.
Аэродинамические характеристики зданий для расчета ветрового воздействия на ограждающие конструкции // Жилищное строительство №1'2010, 2010. С. 711.
6. С.В. Гувернюк, О.О. Егорычев, С.А. Исаев,
Н.В. Корнев, О.И. Поддаева. Численное и физическое
моделирование ветрового воздействия на группу высотных зданий // Научно-технический журнал " Вестник МГСУ", 2011. № 1(3). С. 185–191.