Задача1

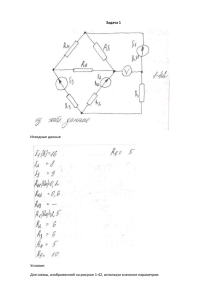
Задача1
Вари-ант
Схема
(рис.)ис.)
Задание: для электрической цепи переменного тока, соответствующей
номеру варианта, с параметрами, приведенными в табл. 6.1, выполнить
следующее:
1. Вычертить заданную цепь, выписать заданные величины э.д.с. и
сопротивлений;
2. Построить схему замещения заданной цепи и определить полные
комплексные сопротивления ветвей электрической цепи;
3. Произвести расчет всех комплексных токов и напряжений на участках
цепи символическим методом;
4. Рассчитать сопряжённые комплексы токов;
5. Вычислить комплексы мощности источника и приёмников; произвести
проверку правильности расчета токов путем составления уравнения баланса
мощностей цепи;
6. Записать мгновенные значения токов и напряжений на участках цепи;
7. Построить векторную диаграмму токов и напряжений в комплексной
плоскости.
1
6.1
Параметры
Сопротивления элементов схемы, Ом
источника
R1
X1
R2
X2
R3
X3
R4
X4
R5
X5
U, В
ψu, град
3
4
4
3
8
6
6
8
0
5
40
60
Пример:
Пример расчета простой цепи переменного тока символическим
методом.
1. Пусть задана схема, изображенная на рис. 6.26, с параметрами: R1 = 5 Ом;
R2 = 10 Ом; R3 = 4 Ом; R4 = 8 Ом; R5 = 6 Ом; X1 = 8 Ом; X2 = 6 Ом; X3 = 10 Ом; X4 =
10 Ом; X5 = 5 Ом; параметры источника: U = 220 B, ψu = 450.
Рис. 6.26. Исходная цепь для расчета
2. Строим схему замещения (рис. 6.27) и определяем комплексные
сопротивления ветвей и комплекс входного напряжения. На схеме
замещения обозначим условные положительные направления токов в
ветвях.
Рис. 6.27. Схема замещения исходной цепи
Полные комплексные сопротивления ветвей схемы замещения:
Z 1  5  j8  9.43 e j 57.99 , Ом
– сопротивление имеет активно-
индуктивный (R-L) характер;
Z 2  10  j 6  11.66 e  j 30.96 , Ом – сопротивление имеет активноемкостный (R-C) характер;
Z 3  4  j10  10.77 e j 68.2 , Ом – сопротивление имеет активноиндуктивный (R-L) характер;
Z 4  8  j10  12.8 e  j 51.34 , Ом – сопротивление имеет активноемкостный (R-C) характер;
Z 5  6  j5  7.81e  j 39.81 , Ом – сопротивление имеет активноемкостный (R-C) характер.
Комплекс входного напряжения:
j 45
U  220 e
 155.56  j 155.56 , В.
3. Произведем расчет комплексных токов и напряжений на всех участках
цепи символическим методом. Для этого найдем комплекс эквивалентного
сопротивления всей цепи (т.е. приведем ее к виду, представленному на рис.
6.28).
Рис. 6.28. Схема с эквивалентным сопротивлением
Определим эквивалентные сопротивления (сначала отдельных
участков схемы замещения, а затем эквивалентное сопротивление всей
цепи):
Z 45 
Z4 Z5
 4.85 e  j 44.18  3.49  j 3.39, Ом ;
Z4  Z5
Z 345  Z 3  Z 4,5  10 e j 41.43  7.49  j 6.61, Ом ;
Z 2345 
Z 2  Z 3, 45
Z 2  Z 3, 45
 6.66 e j 8.47  6.58  j 0.98, Ом ;
Z экв  Z 1  Z 2,345  14.65 e j 37.79  11.58  j8.98, Ом .
Комплексы токов в ветвях можно найти как:
j 45

I 1  U  220 e
 15.02 e j 7.21  14.9  j 1.89 , А
j 37.79
Z экв 14.65 e
j 7.21

 6.66 e j 8.47
I  I 1  Z 2345  15.02 e
 8.58 e j 46.64  5.89  j 6.24 ,
2
 j 30.96
Z2
11.66 e
j 7.21

 6.66 e j 8.47
I  I 1  Z 2345  15.02 e
 10.01e  j 25.77  9.02  j 4.35 ,
3
j 41.43
Z 3, 45
10 e
A
A
 j 25.77

 4.85 e  j 44.18
I 4  I 3  Z 45  10.01 e
 3.8 e  j18.59  3.6  j 1.21 , A
 j 51.34
Z4
12.8 e
 j 25.77

 4.85 e  j 44.18
I 5  I 3  Z 45  10.01 e
 6.24 e  j 30.12  5.39  j 3.13 , A
 j 39.81
Z5
7.81 e
Комплексы напряжений на участках цепи:
U 1  I1  Z 1  141 .64 e j 65.2  59.41  j 128 .58 , B
U 2  I2  Z 2  100 e j15.68  96.28  j 27.03 , B
U 3  I3  Z 3  107 .7 e j 42.43  79.49  j 72.66 , B
U 4  I4  Z 4  48.64 e  j 69.9  16.72  j 45.68 , B
U 5  I5  Z 5  48.64 e  j 69.9  16.72  j 45.68 , B
4. Найдем сопряженные комплексы токов:
*
I 1  14.9  j1.89  15.02 e  j 7.21 , A

I 2  5.89  j 6.24  8.58 e  j 46.64 , A
*
I 3  9.01  j 4.35  10 e j 25.77 , A
*
I 4  3.6  j1.21  3.8 e j18.59 , A
*
I 5  5.39  j3.13  6.24 e j 30.12 , A
5. Вычислим комплексы мощностей источника и приемников. Составим
уравнение баланса мощностей и убедимся в правильности произведенных
расчетов.
Мощность приемников:
S потр  S1  S 2  S 3  S 4  S 5  3304.6 e j 37 .75  2612.77  j 2023.32, BA
,
где
S1 
*
*
I1  I1  Z 1  I1  U 1  2127.4 e j 57.99  1127.67  j1803.95, BA
*
*
*
*
*
*
*
*
S 2  I 2  I2  Z 2  I 2  U 2  858.37 e  j 30 .96  736.08  j 441.58, BA
S3 
I 3  I3  Z 3  I 3  U 3  1077 e j 68.2  399.96  j999.98, BA
S 4 
I 4  I4  Z 4  I 4  U 4  184.8 e  j 51.34  115.46  j144.33, BA
S5 
I 5  I5  Z 5  I 5  U 5  304.1 e  j 39.81  233.6  j194.7, BA
Мощность источника
*
Sист  U  I 1  3304.4 e j 37.79  2611.3  j 2024.8, ВА
Баланс мощностей S ИСТ  S ПОТР сошелся, погрешность не превышает
допустимую величину в 5%.
6. Мгновенные значения токов и напряжений на участках цепи, в общем
виде, выражаются как
i  I m sint   i , u  U m sint   u  ,
где: I m  I  2 – амплитудное значение тока;
U m  U  2 – амплитудное значение напряжения.
 i – начальная фаза тока;
 u – начальная фаза напряжения.
Найдем мгновенные значения токов ветвей:
i1  15.02 2 sin t  7.21 , A
i2  8.58 2 sin t  46.64 , A
i3  10 2 sin t  25.77  , A
i4  3.8 2 sin t  18.59 , A
i5  6.24 2 sin t  30.12 , A ,
а также мгновенные значения напряжений на участках цепи:
u1  141.64 2 sin t  65.2  , B
u 2  100 2 sin t  15.68 , B
u 3  107.7 2 sin t  42.43 , B
u 4  48.64 2 sin t  69.93 , B
u 5  48.64 2 sin t  69.93 , B
7. Строим векторную диаграмму токов и напряжений в комплексной
плоскости (рис. 6.29).
Рис. 6.29. Векторная диаграмма токов и напряжений
Задача 2
Вариант
задания
1
Схема
(№
рисунка)
7.1
Параметры элементов схемы, Ом
Ra (Rab) Xa (Xab) Rb (Rbc) Xb (Xbc) Rc (Rca) Xc (Xca)
5
3
5
8
7
4
Задание: для электрической цепи трехфазного переменного тока,
соответствующей номеру варианта, с параметрами, приведенными в
таблице 7.1, выполнить следующее:
1. Вычертить заданную цепь, выписать заданные величины э.д.с. и
сопротивлений;
2. Построить схему замещения заданной цепи и определить полные
комплексные сопротивления каждой из фаз нагрузки;
3. Произвести расчет комплексных фазных и линейных токов, а также тока в
нейтральном проводе (при его наличии в заданной схеме), комплексных
напряжений на каждом из элементов всех фаз нагрузки;
4. Найти активную, реактивную и полную мощности каждой фазы и всей
цепи; произвести проверку правильности расчета токов путем составления
уравнения баланса мощностей цепи;
5. Записать мгновенные значения токов и напряжений на каждом из
элементов всех фаз нагрузки;
6. Построить векторную диаграмму токов и напряжений в комплексной
плоскости.
7. При выполнении задания по каждому из вариантов принять, что заданная
схема питается от симметричного трехфазного источника э.д.с., при этом
действующее значение э.д.с. каждой из фаз источника равно 220 В.
Пример 2.
В четырехпроводную трехфазную сеть с линейным напряжением
Uл=220 В включен по схеме «звезда с нулевым проводом» приемник,
активные и индуктивные сопротивления фаз которого соответственно равны:
ra=3 Ом, xa=4 Ом, rb =3 Ом, xb=5,2 Ом, rc=4 Ом, xc=3 Ом (рис. 7.28).
Требуется определить токи в линейных и нейтральном проводах и
построить векторную диаграмму токов и напряжений.
Решение. Считаем, что вектор фазного напряжения U a направлен по
действительной оси, тогда
U
U a  л  127 B; U b  127e  j120
3
B; U c  127e j120
Находим линейные токи:
U
127
127
Ia  a 
 j 53  25,4e  j 53
Z
3  j 4 5e
A;
 a
U
127e  j120 127e  j120
Ib  b 

 21,2e  j180
j 60
Z
3  j 5.2
6e
 b
j120

127e j120
I  U c  127e

 25,4e j 83
c
Z
43j
5e j 37
 c
A;
A;
B
Рис. 7.28. Схема для расчета
Ток в нейтральном проводе определяется как геометрическая сумма
линейных токов:
IN  Ia  Ib  Ic  25.4e  j 53  21.2e  j180  25.4e j 83  5.9e j124
A;
Векторная диаграмма приведена на рис. 7.29.
При несимметричной нагрузке для определения активной мощности
находят мощность каждой фазы отдельно:
Pф  U ф I ф cos 
,
а мощность всей трехфазной системы получают как сумму мощностей всех
фаз.