Баланс мощностей в электрической цепи

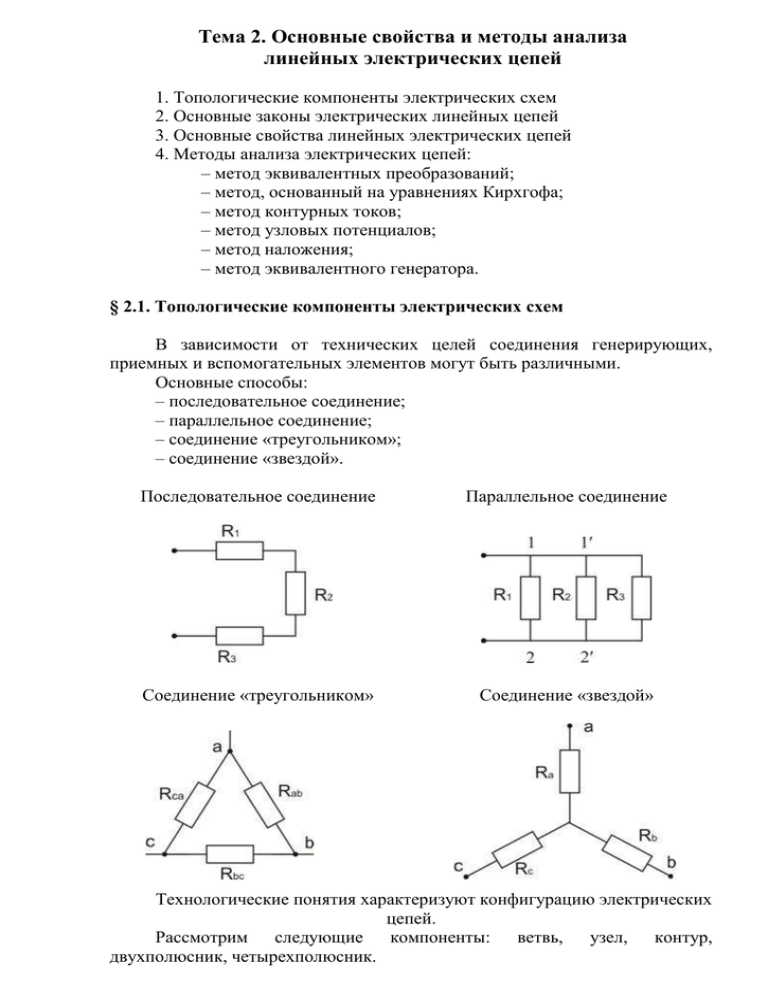
Тема 2. Основные свойства и методы анализа
линейных электрических цепей
1. Топологические компоненты электрических схем
2. Основные законы электрических линейных цепей
3. Основные свойства линейных электрических цепей
4. Методы анализа электрических цепей:
– метод эквивалентных преобразований;
– метод, основанный на уравнениях Кирхгофа;
– метод контурных токов;
– метод узловых потенциалов;
– метод наложения;
– метод эквивалентного генератора.
§ 2.1. Топологические компоненты электрических схем
В зависимости от технических целей соединения генерирующих,
приемных и вспомогательных элементов могут быть различными.
Основные способы:
– последовательное соединение;
– параллельное соединение;
– соединение «треугольником»;
– соединение «звездой».
Последовательное соединение
Параллельное соединение
Соединение «треугольником»
Соединение «звездой»
Технологические понятия характеризуют конфигурацию электрических
цепей.
Рассмотрим следующие компоненты: ветвь, узел, контур,
двухполюсник, четырехполюсник.
Ветвь – участок электрической цепи с одинаковой величиной тока.
Ветви могут быть пассивными (не содержат источник) и активными
(содержат источник).
Узел – место соединения трех и более ветвей. В схеме электрической
цепи различают геометрические и потенциальные узлы.
Контур – замкнутое очертание участков цепи, проходящее через ветви и
узлы.
Двухполюсник – часть электрической цепи с выделенными двумя
зажимами (полюсами), с помощью которых этот участок присоединяется к
цепи. Он может быть активным и пассивным. Также двухполюсник может
состоять из одного элемента.
Четырехполюсник – часть электрической цепи с выделенными
четырьмя зажимами, с помощью которых он присоединяется к электрической
цепи.
§ 2.2. Основные законы электрических линейных цепей
Первый закон Кирхгофа (1ЗК): алгебраическая сумма токов в любом узле
равна 0:
Замечание 1. При записи уравнения учитывается направление тока в ветви по
отношению к узлу. Условимся, что если ток идет к узлу – «–», от узла – «+».
Замечание 2. Если к узлу присоединена ветвь с идеальным источником тока, то ток
этой ветви равен току источника и учитывается при записи 1ЗК.
Второй закон Кирхгофа (2ЗК): алгебраическая сумма падений
напряжений на всех элементах любого контура электрической цепи равна 0:
Замечание 1. При записи уравнения задаемся направлением обхода контура. Если
направление обхода совпадает с положительным направлением напряжения, то оно
учитывается в уравнении со знаком «+», иначе – «–».
Замечание 2. Если учесть, что падение напряжения на всех резистивных элементах
равно
, а падения напряжения равно
, то:
падения напряжения на всех пассивных
элементах контура, включая внутреннее
сопротивление
ЭДС идеальных источников напряжения
Правила знаков такие же.
Замечание 3. Иногда контур электрической цепи
включает в себя напряжение между двумя зажимами.
Тогда это учитывается при записи уравнения в левой
части последнего выражения.
По умолчанию считается, что положительное
направления напряжения на пассивных элементах
совпадает с направлением тока.
Баланс мощностей в электрической цепи
В любой автономной электрической цепи суммарная мощность
источников электрической энергии равна суммарной мощности приемников.
§ 2.3. Основные свойства линейных электрических цепей
1. Для линейных электрических цепей справедлив принцип
независимости действия возбуждающих сил, то есть источников напряжения и
тока. Этот принцип называется принципом наложения (суперпозиции). Его
формулировка: «Ток в любой ветви электрической цепи равен алгебраической
сумме токов, действующих от каждого источника в отдельности». Этот
принцип лежит в основе метода наложения.
2. В линейных электрических цепях существует однозначность
электрического состояния.
3. В линейных электрических цепях существует линейная зависимость
между электрическими параметрами, то есть токами и напряжениями:
,
где
– токи в ветвях с номерами
;
– напряжение между точками a и b.
Это свойство лежит в основе метода эквивалентного генератора.
§ 2.4. Методы анализа электрических цепей
Анализ электрических цепей заключается в следующем.
Задана схема электрической цепи (графически или аналитически). Для
схемы известны ЭДС всех источников напряжения, токи всех источников
тока с их внутренними сопротивлениями или проводимости. Заданы
сопротивления всех резистивных элементов схемы. Требуется определить
токи во всех элементах электрической цепи.
Отметим:
1. Часто в задании цепи отсутствует
и
. Это может объясняться
следующим: либо
и
можно пренебречь, либо их значения уже
учтены в сопротивлениях соответствующих ветвей.
2. Так как по всем элементам ветви протекает один и тот же ток, то
достаточно определить токи во всех ветвях электрической цепи.
3. Зная токи ветвей, можно решить любую другую задачу. Например,
найти:
4. Правильность расчета режима электрической цепи проверяется
проверкой баланса мощностей.
§ 2.4.1. Метод эквивалентных преобразований
Этот метод применим либо к отдельным участкам сложной
электрической цепи, либо к электрической цепи, в которой действует один
источник.
Проведя
по
определенным
правилам
эквивалентные
преобразования, можно свести электрическую цепь к виду:
зависит от способа соединения пассивных элементов.
Рассчитать эту схему и, используя законы Кирхгофа и Ома, можно
определить обратным ходом токи всех ветвей.
Самостоятельно!!! Рассмотреть: последовательное, параллельное,
смешанное соединение и соединения «треугольником» и «звездой».
План каждого соединения:
– схема соединения;
– основные свойства этого соединения;
– формулы эквивалентных преобразований;
– пример.
Книги:
1. Волынский В.А. и др. «Электротехника», 1987 г. (С. 37-41);
2. Электротехника под ред. В. Г. Герасимова. С. 22-27.;
3. Касаткин «Электротехника».
В зависимости от назначения электрической цепи ее элементы
(источники, приемники, вспомогательные элементы) могут соединяться
различным образом. Существует четыре основных вида соединений
элементов: последовательное, параллельное, «треугольником», «звездой» и
смешанное.
1. Последовательным называется соединение, при котором ток в
каждом
элементе
один
и
тот
же.
При
последовательном
соединении n пассивных
элементов
цепи.
Схема
замещения
с n резистивными элементами может быть заменена эквивалентной схемой с
одни резистивным элементом.
По 2ЗК:
Например:
2. Параллельным называется соединение, при котором все участки цепи
присоединяются к одной паре узлов, то есть находятся под воздействием
одного и того же напряжения.
Рис. Схема замещения цепи с параллельным соединением пассивных
элементов и ее эквивалентная схема
Ток в каждой ветви определяется напряжением и сопротивлением:
.
Условия эквивалентности будут соблюдены, если ток эквивалентной
схемы будет равен току в неразветвленной части цепи, то
есть
.
В результате получаем:
,
из которой получают формулу для эквивалентного сопротивления:
или для эквивалентной проводимости:
Эквивалентное сопротивление параллельно соединенных элементов
обратно пропорционально ее эквивалентной проводимости:
,
поэтому оно всегда меньше наименьшего из сопротивления цепи.
Если
параллельно
соединены n ветвей
с
одинаковыми
сопротивлениями R , то их эквивалентное сопротивление будет в n раз
меньше сопротивления каждой ветви, то есть
.
Параллельное соединение обеспечивает одинаковое напряжение на
всех включенных приемниках.
3. Смешанное соединение резистивных элементов. При наличии в цепи
одного источника внешнюю по отношению к нему часть схемы можно в
большинстве случаев рассматривать как смешанное (последовательнопараллельное) соединение резистивных элементов.
Для расчета такой цепи удобно преобразовать ее схему замещения в
эквивалентную схему с последовательным соединением резистивных
элементов.
Между
узлами a и b включены
3
резистивных
элемента
с
сопротивлениями
,
и
.
После замены параллельного соединения резистивных элементов
эквивалентным резистивным элементом с сопротивлением
получается эквивалентная схема с последовательным соединением двух
резистивным элементов
и
.
Ток в неразветвленной части:
Токи в параллельных ветвях:
где
.
.
4. В некоторых сложных электрических цепях встречаются соединения
элементов, которые нельзя отнести к вышеперечисленным. Типичным
примером подобной сложной цепи является мостовая цепь.
Рис. Схема замещения мостовой цепи и ее эквивалентная схема
В этом случае часть цепи образует «треугольник», вершинами которого
являются три узла (a, b, c), а сторонами – три ветви с сопротивлениями
,
,
, включенных между этими узлами. Расчет такой цепи удобно
проводить, используя эквивалентную замену трех ветвей, соединенных
«треугольником», тремя ветвями, соединенными трехлучевой «звездой». При
замене соединения «треугольником» ветвей с сопротивлениями
,
ветвями с сопротивлениями
,
мостовая цепь преобразовывается в
параллельным соединением элементов.
,
,
, соединенных «звездой»,
цепь с последовательным и
Для определения сопротивления
,
,
ветвей, соединенных
«звездой», необходимо найти соотношения, связывающих их с
сопротивлениями ветвей, соединенных «треугольником». С этой целью
воспользуемся общим условием эквивалентности, по которым напряжения и
токи в ветвях, не подвергнутых преобразованию, должны оставаться без
изменения в любых режимах, в точности при размыкании ветвей,
присоединенных к узлам a, b, c.
При отсоединении ветви с сопротивлением
также
напряжение
равны
от узла a токи
соответствующим
токам
,а
и
и
напряжению
в схеме (б), то есть сопротивления между точками b и c для
обеих схем (а) и (б) одинаковы:
.
При отсоединении ветви
от узла с сопротивление между
точками a и b для обеих схем по условию эквивалентности должны быть
также одинаковы:
.
Аналогично между точками a и c:
.
Решая систему из трех уравнений, получаем:
В ряде случаев схему соединения ветвей «звездой» целесообразно
преобразовывать схему соединения ветвей «треугольником». При
эквивалентной замене ветвей, соединенных трехлучевой «звездой», ветвями,
соединенными «треугольником», сопротивления ветвей «треугольником»
можно определить, зная сопротивления ветвей «звезды»:
в случае замены трех одинаковых ветвей, соединенных
«треугольником», тремя ветвями, соединенными «звездой», сопротивления
новых ветвей будет в три раза меньше сопротивлений прежних ветвей, то
есть:
§ 2.4.2. Метод, основанный на уравнениях Кирхгофа
Алгоритм метода:
1. Определяется число узлов
, число ветвей
и произвольно
задаются направления токов в каждой ветви. Таким образом, число
неизвестных токов равно
.
2. Для всех узлов, кроме любого одного записываются уравнения по
1ЗК. Ток источника тока учитывается как ток ветви. Всего этих
уравнений
3.
где
.
Определяется
число
независимых
контуров:
,
– число ветвей, исключая ветви с источником тока. Выбираются
независимые контуры и задаются направления обхода каждого из них. При
выборе независимых контуров следует учесть:
– каждый выбранный следующий контур должен иметь хотя бы одну
ветвь, не входящую в предыдущий;
– ветви с источниками тока контуров не создают, то есть контур не
может замыкаться по ветви с источником тока.
4. Для заданного контура записываются уравнения по 2ЗК. Всего
уравнений
.
5. Решается система уравнений, записанных в пунктах 2 и 4. Эта
система содержит
уравнений. Или
. В
результате определяются токи всех ветвей электрической цепи.
6.
Правильность
расчета
проверяется балансом мощностей.
1ЗК:
1 узел:
.
2 узел:
3 узел:
.
.
2ЗК:
1
контур:
2
.
контур:
3
контур:
Схема для примера:
.
.
,
,
.
Баланс мощностей:
§ 2.4.3. Метод контурных токов (МКТ)
Он позволяет сохранить число алгебраических уравнений системы до
числа контуров. Он выводится на основании ЗК и является следствием этих
законов.
1.
,
,
. Задаются положительные направления токов ветвей.
2. Источники тока преобразовываются в источники напряжения.
3. Для всех контуров задаются фиктивные контурные токи,
циркулирующие по всем ветвям контура в произвольном направлении.
4. Записывается контурное уравнение
– столбец неизвестных контурных токов.
– матрица контурных
сопротивлений.
Свойства:
а)
б)
;
– всегда положительная сумма всех сопротивлений контура;
в)
– сумма сопротивлений, общих для контура i и j (эта сумма
берется со знаком «+», если в общей ветви контурные токи направлены
согласно, и со знаком «–», если они направлены встречно).
– матрица контурных ЭДС (составляется также, как и для
2ЗК).
Решают контурное уравнение и определяют все контурные токи.
5. По найденным контурным токам на основании ЗК определяются
токи во всех элементах исходной схемы.
6. Проверяется баланс мощностей.
§ 2.4.4. Метод узловых потенциалов (МУП)
Позволяет сократить число уравнений системы до числа узлов (
).
Он также вытекает из законов Кирхгофа.
1. Определяется число узлов, ветвей и задается положительное
направление тока.
2. Все источники напряжения преобразуются в источники тока.
3. Потенциал одного из узлов принимается равным 0 (
4. Для оставшихся (
).
) узлов записывается узловое уравнение
– столбец неизвестных потенциалов.
Свойства:
а)
б)
в узле i;
;
– всегда положительная сумма проводимости ветвей, сходящихся
в)
– всегда отрицательная сумма проводимости всех ветвей,
соединяющих узлы i и j.
– столбец узловых токов.
Каждый элемент этого столбца – алгебраическая сумма источников
тока, присоединенных к узлу. При этом, если источник направлен к узлу, то
его ток учитывается со знаком «+». Если от узлу – «–».
Пример.
§ 2.4.5. Метод наложения (суперпозиции) – самостоятельно!!!
Принцип наложения: ток в k-той ветви равен алгебраической сумме
токов, вызываемых каждой из ЭДС схемы в отдельности.
Этот принцип справедлив для всех линейных электрических цепей, он
положен в основу метода расчета, получившего название метода наложения.
При расчете цепей данным методом поступают следующим образом:
поочередно рассчитывают токи, возникающие от действия каждой из ЭДС,
мысленно удаляя остальные из схемы, но оставляя в схеме внутренние
сопротивления источников, и затем находят токи в ветвях путем
алгебраического сложения частичных токов.
Замечание. Методом наложения нельзя пользоваться для подсчета выделяемых в
сопротивлении мощностей как суммы мощностей от частичных токов, поскольку
мощность является квадратичной функцией тока (
).
Если через резистор протекают согласно направленные частичные
токи
и
, выделяемая в нем мощность
мощностей от частичных токов:
и не равна сумме
.
С помощью схемы (б) (источник ЭДС удален и зажимы cd закорочены)
найдем токи в ветвях от действия ИТ:
.
Используя схему (в), подсчитаем токи в ветвях от действия источника
ЭДС (зажимы ab разомкнуты, так как внутреннее сопротивление ИТ = ):
.
Результирующие токи в ветвях вычислим, алгебраически суммируя
соответствующие частичные токи этих двух режимов:
Мощность, отдаваемая в схему источником тока равна:
.
Мощность, отдаваемая в схему источником ЭДС равна:
.
Уравнение баланса мощности:
.
§ 2.4.6. Метод эквивалентного генератора
Позволяет определить ток в отдельной ветви электрической цепи.
Допустим, надо определить ток
в сопротивлении
.
1. Из исходной схемы исключается сопротивление
и остаются
зажимы, к которым это сопротивление было присоединено. Допустим,
зажимы a и b.
2. Рассчитывается режим работы новой схемы (без сопротивления
в результате чего определяется напряжение
напряжение ХХ.
),
. Это напряжение –
3. В преобразованной схеме (без сопротивления
) проводится
исключение всех источников. Источники напряжения задаются только своим
внутренним напряжением (без ЭДС), а источники тока только своей
внутренней проводимостью. То есть идеальные источники напряжения
закорачиваются, а идеальные источники тока выбрасываются.
Относительно зажимов ab определяется эквивалентное сопротивление (
) по правилам эквивалентных преобразований. Это
– входное
сопротивление.
4. Вся схема относительно выделенных зажимов заменяется
эквивалентным генератором ЭДС: