Новый широкоугольный телескоп

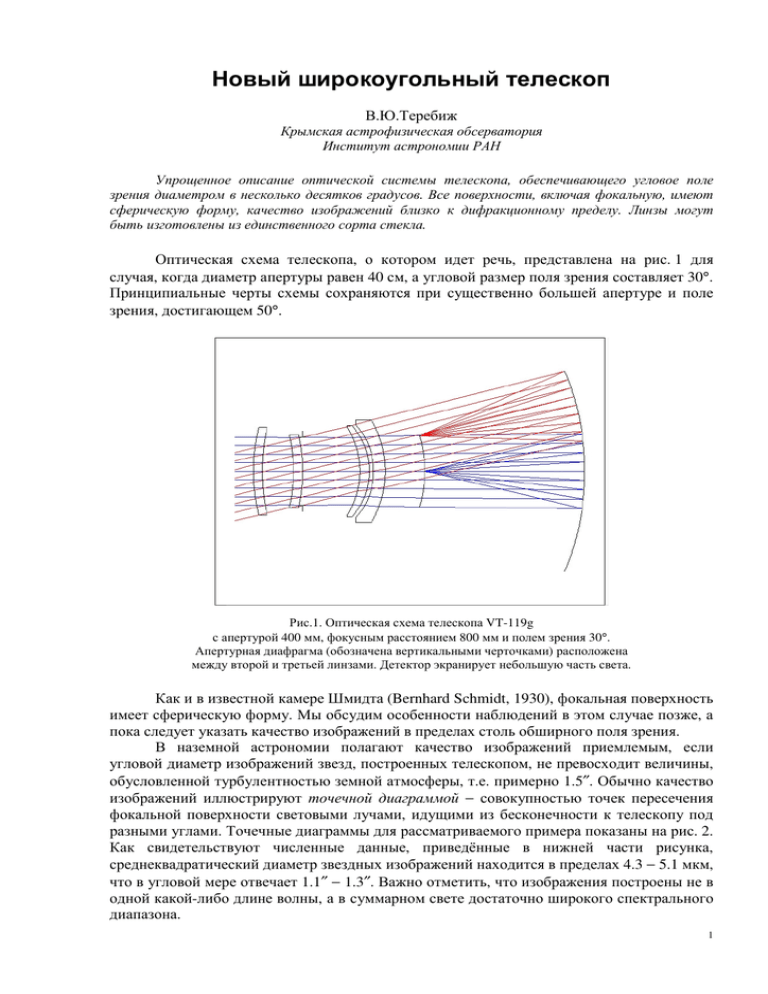
Новый широкоугольный телескоп
В.Ю.Теребиж
Крымская астрофизическая обсерватория
Институт астрономии РАН
Упрощенное описание оптической системы телескопа, обеспечивающего угловое поле
зрения диаметром в несколько десятков градусов. Все поверхности, включая фокальную, имеют
сферическую форму, качество изображений близко к дифракционному пределу. Линзы могут
быть изготовлены из единственного сорта стекла.
Оптическая схема телескопа, о котором идет речь, представлена на рис. 1 для
случая, когда диаметр апертуры равен 40 см, а угловой размер поля зрения составляет 30°.
Принципиальные черты схемы сохраняются при существенно большей апертуре и поле
зрения, достигающем 50°.
Рис.1. Оптическая схема телескопа VT-119g
с апертурой 400 мм, фокусным расстоянием 800 мм и полем зрения 30°.
Апертурная диафрагма (обозначена вертикальными черточками) расположена
между второй и третьей линзами. Детектор экранирует небольшую часть света.
Как и в известной камере Шмидта (Bernhard Schmidt, 1930), фокальная поверхность
имеет сферическую форму. Мы обсудим особенности наблюдений в этом случае позже, а
пока следует указать качество изображений в пределах столь обширного поля зрения.
В наземной астрономии полагают качество изображений приемлемым, если
угловой диаметр изображений звезд, построенных телескопом, не превосходит величины,
обусловленной турбулентностью земной атмосферы, т.е. примерно 1.5″. Обычно качество
изображений иллюстрируют точечной диаграммой − совокупностью точек пересечения
фокальной поверхности световыми лучами, идущими из бесконечности к телескопу под
разными углами. Точечные диаграммы для рассматриваемого примера показаны на рис. 2.
Как свидетельствуют численные данные, приведённые в нижней части рисунка,
среднеквадратический диаметр звездных изображений находится в пределах 4.3 − 5.1 мкм,
что в угловой мере отвечает 1.1″ − 1.3″. Важно отметить, что изображения построены не в
одной какой-либо длине волны, а в суммарном свете достаточно широкого спектрального
диапазона.
1
Рис.2. Расчетные изображения звезды
в телескопе VT-119g на оптической оси
и на угловых расстояниях
5°, 7.5°, 10°, 12.5° и 15° от неё.
Изображения построены в суммарном свете
диапазона длин волн 0.45 - 0.85 мкм.
Сторона каждого квадратика − 11.6 мкм (3″).
Центральный диск в дифракционной картине
Эри диаметром 3.1 мкм (0.8″) обозначен
кружком.
Для того чтобы оценить характеристики предлагаемой системы и понять, зачем
понадобилась достаточно странная оптическая схема, нам придется напомнить некоторые
особенности телескопов, определяющие размеры их поля зрения. Сопутствующие заметки
по необходимости фрагментарны и не следуют исторической эволюции телескопов, их
задача − бегло наметить положение дел, сложившееся в области широкоугольных
астрономических систем.
Поле зрения телескопов
Как известно, изображения звезд, образованные сферическим зеркалом, размыты
сферической аберрацией, не исчезающей даже на оптической оси (рис. 3). Сферическая
аберрация становится пренебрежимо малой, когда фокусное расстояние F зеркала
значительно превосходит его диаметр D, иными словами, когда фокальное отношение
φ ≡ F/D значительно больше единицы. Этот случай нетипичен для оптической
астрономии, а потому простой телескоп в виде одиночного сферического зеркала
используется редко.
Рис. 3. Сферическая аберрация зеркала
сферической формы для осевого пучка света:
лучи, отраженные от краев зеркала, собираются
ближе к нему, чем лучи, идущие вблизи
оптической оси.
В XIII веке Эразм Вителло (Vitellius) указал, что изображения на оптической оси
становятся идеальными, если зеркалу придать форму параболоида. Строго говоря,
качество осевого изображения звезды ограничено неизбежной дифракцией света;
внеосевые изображения по-прежнему искажены ещё и совокупностью разного рода
геометрических аберраций, прежде всего − комой (рис. 4). Столетие тому назад астрономы
пользовались простым правилом Зоннефельда (August Sonnefeld), согласно которому поле
зрения параболоида, выраженное в минутах дуги, примерно равно фокальному
отношению: 2w′ ≈ φ. Так, при φ = 4 угловое поле по Зоннефельду составляет лишь около
4′; современные требования снижают эту оценку, по крайней мере, вдвое. Поэтому при
наблюдениях с одиночным зеркалом часто используют линзовый корректор поля
сравнительно небольшого размера.
2
Рис. 4. Монохроматические изображения звезды на оптической оси и на удалении 1′ и 2′ от неё,
образованные идеальным параболоидом диаметром 1 м с фокусным расстоянием 4 м
(логарифмический масштаб яркости). Сторона каждого квадрата соответствует 10″.
В классических двухзеркальных телескопах (рис. 5) изображение, построенное
параболическим главным зеркалом, перебрасывается вторичным зеркалом в область,
расположенную вне падающего пучка. Более существенно, что при этом увеличивается
фокальное отношение телескопа φ и, как следствие, уменьшаются внеосевые аберрации,
достигается более широкое поле зрения. В классических системах оно составляет
несколько угловых минут.
Рис. 5. Классические телескопы Грегори (1663) и Кассегрена (1672).
Первый включает в себя параболическое главное зеркало и эллиптическое вторичное зеркало;
во втором − параболическое главное зеркало сочетается с гиперболическое вторичным зеркалом.
Схемы Грегори (James Gregory) и Кассегрена (Laurent Cassegrain) последовательно
доминировали в астрономии с XVIII века до середины XX века, когда на смену последней
пришла система Ричи-Кретьена (G.W. Ritchey, H. Chretien, сокращенно RC). В схеме RC
оба зеркала представляют собой гиперболоиды, поэтому сферическая аберрация немного
размывает изображения в первичном фокусе даже на оси, но появление еще одного
свободного параметра − эксцентриситета главного зеркала − позволяет уменьшить кому
во вторичном фокусе. Угловое поле систем RC достигает 15′ – 20′, что заметно расширяет
круг решаемых астрономических задач. Это явилось главной причиной при выборе схемы
RC для космического телескопа имени Хаббла (E. Hubble Space Telescope); необычно
большое фокальное отношение φ = 24 обеспечивает здесь поле размером 20′.
Если в системе RC предполагаются наблюдения не только во вторичном, но и в
первичном фокусе, то приходится устанавливать корректор поля, сходный с теми, что
используются в классических телескопах.
Аналогична эволюция классической схемы Грегори, поле зрения которой
Дмитрий Максутов увеличил, заменив параболическое главное зеркало эллипсоидальным.
3
Оба типа двухзеркальных телескопов с улучшенными изображениями, РичиКретьена и Максутова, относятся к классу апланатов − оптических систем с заметно
уменьшенными сферической аберрацией и комой. Угловое поле зрения двухзеркальных
апланатов достигает примерно 1/3 градуса. Дальнейшее расширение поля требует
введения в системы с двумя зеркалами дополнительных оптических элементов − зеркал,
линз или элементов обоих видов.
Рис. 6. Оптическая схема космического телескопа
SNAP системы Корша (плоское зеркало с отверстием
в центре введено в схему для уменьшения
экранирования света).
Диаметр апертуры равен 2 м, угловой диаметр поля
зрения составляет 1.5° при полном виньетировании
центральной части диаметром 0.7°.
На первом пути наибольшего успеха добился в начале 1970-х годов Корш (Dietrich
Korsch); один из вариантов его трехзеркального телескопа показан на рис. 6. Оказалось,
что трех зеркал с поверхностями в виде обычных конических сечений достаточно, чтобы
устранить все 5 аберраций третьего порядка: сферическую аберрацию, кому, астигматизм,
дисторсию и кривизну поля! Поэтому телескоп Корша строит превосходные изображения
в пределах плоского поля диаметром до 2°. Это обстоятельство, а также чрезвычайно
широкий спектральный диапазон, доступный чисто зеркальной системе, послужили
основными причинами при выборе системы Корша для многообещающего космического
проекта Super-Nova Acceleration Probe (SNAP).
Рис. 7. Линзовые корректоры в прямом (слева) и в кассегреновском фокусах телескопа.
Ещё более широкого углового поля зрения − диаметром до 3.5° − удалось достичь
со сравнительно небольшими линзовыми корректорами, расположенными вблизи прямого
или кассегреновского фокусов (рис. 7). Таковы оптические схемы большинства крупных
телескопов. Значительная апертура этих инструментов позволяет наблюдать слабые
объекты, однако размеры поля зрения всё же недостаточны для решения ряда важных
задач, стоящих перед современной астрономией, в частности, построения шкалы
внегалактических расстояний с помощью Сверхновых звезд, изучения мощных
γ-всплесков излучения, поисков т.н. темной энергии, а также объектов, ассоциирующихся
с источниками гравитационных волн. Если к этим задачам добавить широко обсуждаемую
ныне проблему астероидной опасности, то станет понятно, почему сейчас прилагается
4
столько усилий для создания системы регистрации всей небесной сферы вплоть до
примерно 23-й звездной величины с частотой обновления данных несколько раз в сутки.
Рис. 8. Слева показана базовая схема, состоящая из сферического зеркала
и диафрагмы в центре кривизны зеркала С. Камера Шмидта (справа) дополняет
базовую схему асферической коррекционной пластиной, размещенной внутри диафрагмы.
В этой связи естественно обратиться к замечательной системе Шмидта, которая
обеспечивает поле зрения диаметром 5°-10° (рис. 8). Исходной для Шмидта была
изображенная слева на рис. 8 простая схема широкоугольного инструмента, неоднократно
обсуждавшаяся оптиками, начиная с середины XIX века (Joseph Petzval, Herman Vogel,
Karl Strehl). Поскольку сфера симметрична относительно своего центра, пучки света,
проходящие под разными углами через центр, порождают идентичные изображения.
Таким образом, базовая схема обеспечивает огромное поле зрения, но при заметных
размерах диафрагмы изображения звезд будут искажены сферической аберрацией (рис. 3).
Понятно, что астрономы заинтересованы в том, чтобы диафрагма, т.е. апертура телескопа,
была по возможности велика, но тогда поле зрения будет заполнено одинаково
размытыми изображениями.
Сферическую аберрацию можно трактовать так, как будто зеркало вблизи края
каждого пучка света обладает несколько большей оптической силой, чем зона вокруг оси
пучка (см. рис. 3). Это соображение побудило Шмидта поместить внутрь диафрагмы
коррекционную пластину, оптическая сила которой изменяется в противоположном
направлении − убывает от центра к краю. Выполненный Шмидтом расчет показал, что для
коррекции сферической аберрации зеркала одна из поверхностей пластины должна иметь
сложную форму, описываемую уравнением 4-го порядка относительно радиальной
координаты. Тем не менее, Шмидту удалось при помощи остроумного метода изготовить
коррекционную пластину должной формы для своего первого телескопа диаметром 36 см
с фокальным отношением φ = 1.75 и полем зрения 4° (рис. 9).
Важность подхода, который столь успешно развил Шмидт, заключается не только в
том, что был создан первый действительно обзорный телескоп, но и в смене привычной
осевой симметрии телескопов на точечную симметрию относительно центра
сферического зеркала. Именно это обстоятельство позволило радикально увеличить поле
зрения телескопа.
Однако то же стремление сделать равноценными пучки света, приходящие от
протяженного объекта наблюдений, обусловило искривленную, близкую к сферической,
форму фокальной поверхности камеры Шмидта. До тех пор, пока приемником света была
эмульсия, это свойство заставляло либо использовать узкую фотографическую ленту,
либо изгибать тонкие фотопластинки. Производство ПЗС-матриц с поверхностью
произвольной формы началось только недавно, а потому, например, приемник
знаменитого космического телескопа Kepler1, открывшего сотни планет около близких
звезд, состоял из 21-й пары небольших плоских матриц, расположенных на сферической
1
Kepler представляет собой камеру Шмидта с апертурой 95 см и полем зрения эквивалентного диаметра
11.6°. Сферическая аберрация намеренно устранена не полностью для улучшения точности фотометрии.
5
фокальной поверхности; перед каждой такой парой была установлена дополнительная
оптика, обеспечивающая локально плоское поле.
Рис. 9. Пробная фотография2, полученная Шмидтом
с его первой камерой весной 1931 г. Время экспозиции 120 минут.
Оптическая сила коррекционной пластины в камере Шмидта невелика, так что её
рабочая поверхность мало отличается от плоскости. Тем не менее пластина вносит
хроматизм, и потому в светосильных камерах корректирующий элемент нередко состоит
из двух пластин, сделанных из стекла различных сортов. Кроме того, желая улучшить
изображения, перед фокусом устанавливают дополнительную линзовую систему; обычно
она состоит из трех сферических линз, сделанных из непростого стекла. Все эти меры
позволяют довести угловое поле модифицированной камеры Шмидта примерно до 12°,
однако при этом теряется элегантность изначальной системы, изображенной на рис. 8.
Сознавая, что с изготовлением сложной асферической поверхности коррекционной
пластины справятся лишь немногие оптики, Шмидт в 1934 г. сделал первый шаг в деле
создания широкоугольной системы со всеми сферическими поверхностями. Сначала он
рассчитал телескоп, в котором асферическая коррекционная пластина заменена двумя
сферическими линзами, а затем изготовил и испытал в реальных наблюдениях модель с
тремя сферическими линзами3. Испытания были успешными, и лишь преждевременная
кончина Бернхарда Шмидта в 1935 г. задержала распространение полностью сферической
системы. В начале 1940-х годов двухлинзовая система подобного рода была патентована
Рихтером и Слефогтом (R. Richter, H. Slevogt), а трехлинзовая − Хогтоном (J.L. Houghton).
Полностью сферические системы Шмидта-Хогтона и Рихтера-Слефогта легли в
основу производства телескопов с полем зрения вплоть до ~1.5°, в которых нуждались
наука и техника во второй половине XX века, однако для обзорных астрономических
2
Copyright ©2010-2015 Hamburger Sternwarte, Fachbereich Physik, MIN-Fakultät, Universität Hamburg.
Модель хранится в музее Шмидта обсерватории Гамбург-Бергедорф, Германия. Сходная система, однако, с
асферическими поверхностями, показана на рис. 11а.
3
6
работ поле было слишком мало, а качество изображений − далеко не отвечающим
появившимся электронным приемникам света. Для того чтобы вернуть размеры поля
зрения к значениям около 10° при надлежащем качестве изображений на плоской
фокальной поверхности, потребовалось значительное усложнение этих систем в течение
последних 15 лет (рис. 10). По-видимому, системы такого рода достигли оптимального
компромисса в отношении размеров апертуры, диаметра плоского поля зрения, качества
изображений и технологических требований.
Рис. 10. Система Шмидта-Хогтона,
модифицированная автором.
Все оптические поверхности − сферы,
апертура 500 мм, плоское поле зрения
диаметром 10°, размер звездных
изображений − около 2″.
Апертурная диафрагма
(отмечена вертикальными отрезками)
расположена перед главным зеркалом.
Наряду с описанной выше линией развития широкоугольных систем с середины
1950-х годов интенсивно развивалось направление, инициированное запуском первых
спутников Земли. Нужно было создать оптические системы диаметром около полуметра с
полем зрения порядка 20° - 30°, пусть даже и при искривленной фокальной поверхности.
В США эту задачу, в основном, решила камера Бэйкера - Нанна (J.G. Baker, J. Nunn),
оптическая схема которой показана на рис. 11, а в СССР − камера ВАУ Д. Максутова М. Сосниной, представлявшая собой развитие системы Хокинс - Линфута (D.G. Hawkins,
E.H. Linfoot, 1945).
Рис. 11. Слева − камера Бэйкера-Нанна диаметром 500 мм с полем зрения 20°;
справа − камера Бэйкера Супер-Шмидт с апертурой 400 мм и полем 24°.
Все эти схемы берут начало в двух исходных версиях камеры Шмидта при более
широком использовании асферических поверхностей. Так, четыре внутренние
поверхности трехлинзового корректора камеры Бэйкера-Нанна суть асферики 6-го и 8-го
порядков, но желаемого качества изображений достигнуть не удалось − размеры звездных
изображений изменяются от 40 мкм в центре поля до 90 мкм на его краю (17″ - 38″) даже в
узком спектральном диапазоне 0.48 - 0.68 мкм. Камера ВАУ обладала более значительным
полем зрения − 30°, и при этом обеспечивала в несколько раз лучшие изображения, уже
согласующиеся с разрешением фотоэмульсии. Примерно такое же качество изображений
давала камера Супер-Шмидт Бэйкера (рис. 11).
7
Таким образом, эволюция камеры Шмидта привела к созданию обзорных систем
двух типов, характерные примеры которых показаны на рисунках 10 и 11. Системы
первого типа обеспечивают плоское поле зрения достаточно высокого качества размерами
вплоть до 10° при всех сферических поверхностях. Системы второго типа достигают втрое
более широкого углового поля зрения, но при этом используются сложные сорта стекол и
асферические поверхности, фокальная поверхность искривлена, а качество изображений в
несколько раз уступает таковому для систем первого типа.
Новая оптическая система
Всё сказанное в предыдущем разделе имело целью пояснить выбор направления
поисков и основных требований, приведших к простой оптической системе с чрезвычайно
большим полем зрения.
Поскольку, как отмечалось, возможности обзорных систем первого типа достигли
разумного предела, вопрос заключался в следующем: что мешает увеличить размер поля
зрения и в то же время улучшить качество изображений в системах второго типа?
Ответ в значительной мере связан с тем, что асферические элементы корректора в
различных версиях камеры Шмидта неизбежно нарушают центральную симметрию
системы относительно центра кривизны главного зеркала. В самом деле, изображенная
на рис. 8 исходная система − телескоп, состоящий из сферического зеркала и свободной
диафрагмы в его центре,− обеспечивает весьма обширное поле. Поэтому представляется
разумным требование: линзовый корректор должен по возможности сохранить
центральную симметрию исходной системы, для чего нужно полностью
отказаться от использования асферических поверхностей.
Вместе с тем ясно, что этот шаг недостаточен, поскольку следует устранить не
только геометрические аберрации, но и хроматизм системы. Исправление хроматизма, в
особенности, его сочетания со сферической аберрацией − сферохроматизма − дело
непростое, поэтому лучше изначально не вводить его в систему. Легче всего это сделать в
системе с малой оптической силой, т.е. с очень большим фокусным расстоянием4. Задача
линзового корректора − исправить сферическую аберрацию зеркала, однако он должен
сделать это так, чтобы не внести в систему хроматизм. Мы приходим ко второму
требованию: линзовый корректор должен быть близок к афокальной системе, так
что оптическая сила всего телескопа будет почти полностью задаваться
сферическим зеркалом.
Одно из важных понятий в оптике − апертурная диафрагма. Так называют
диафрагму, реально ограничивающую световой поток в оптической системе. В
широкоугольных объективах она обычно расположена внутри системы. Изображение
апертурной диафрагмы предшествующей ей оптикой называют входным зрачком, а
изображение диафрагмы последующей частью оптики − выходным зрачком системы. Оба
зрачка могут быть как действительными, так и мнимыми. Очевидно, через систему
проходит только та часть падающего на неё светового потока, которая попадает в пределы
входного зрачка. В оригинальной камере Шмидта апертурной диафрагмой служит оправа
коррекционной пластины; поскольку перед диафрагмой нет оптических элементов, там же
расположен и входной зрачок. Естественно ожидать, что во всякой системе, обладающей
точечной симметрией, входной зрачок и апертурная диафрагмы совмещены. Поэтому
третье условие можно сформулировать так: следует максимально сблизить входной
зрачок телескопа и его апертурную диафрагму.
Наконец, четвертое условие исходит из того соображения, что для оптических
систем с очень большим полем зрения кривизна фокальной поверхности столь же
естественна, как и для глаза человека. Поэтому не следует устранять кривизну
4
Систему с бесконечно большим фокусным расстоянием называют афокальной.
8
фокальной поверхности; последняя должна иметь форму, диктуемую реальной
симметрией оптической системы.
Последующие поиски системы, которая удовлетворяет всем сформулированным
выше условиям, привели к оптической схеме, показанной на рис. 1. Конечно, это только
одна из реализаций общей схемы такого рода, обеспечивающей поле зрения диаметром в
несколько десятков градусов.
В системе все оптические поверхности суть сферы. Входной корректор состоит из
четырех линз, которые могут быть изготовлены из простейших сортов стекла, В
обсуждаемом здесь примере используется только плавленый кварц (fused silica),
выбранный ввиду его оптической стабильности и прозрачности в широком спектральном
диапазоне.
Апертурная диафрагма следует за первыми двумя линзами. Мнимое изображение
диафрагмы этой парой линз, то есть, по определению, входной зрачок телескопа,
практически совмещен с самой апертурной диафрагмой.
Далее, линзовый корректор близок к афокальной системе: его относительное
фокусное расстояние φ ≈ 61. Вследствие этого изображения свободны от хроматизма в
широком спектральном диапазоне. Хроматическая кривая − зависимость положения
фокуса от длины волны − имеет в полосе 0.45 - 0.85 мкм характерную для апохроматов
S-образную форму с размахом, присущим дифракционно-ограниченным системам.
Наконец, существенное улучшение центральной симметрии привело к тому, что
форма фокальной поверхности в новой системе стала ближе к сферической, чем это имеет
место в камере Шмидта, причем в пределах всего поля качество изображений остается
близким к теоретическому пределу, обусловленному дифракцией света (рис. 2).
Конечно, строгая центральная симметрия системы недостижима, однако следствия
принятых условий вполне оправдывают добавление одной линзы к тому их количеству,
которое потребовалось в камерах Бэйкера - Нанна и Максутова - Сосниной (тем более, что
в нашем случае все поверхности − сферы). Впрочем, Супер-Шмидт Бэйкера (рис. 11)
также содержит четыре линзы, одна из которых используется в двойном прохождении
света. Система с трехлинзовым корректором, сходная с VT-119g, обеспечивает неплохие
изображения, но не более того: хроматизм исправлен недостаточно. С другой стороны,
дальнейшее увеличение количества линз по сравнению с таковым в показанной на рис. 1
схеме тоже нельзя считать оправданным, поскольку выигрыш в качестве изображений уже
невелик.
Ближайшее будущее обзорных систем неизбежно связано с использованием
неплоских детекторов света. Следует ожидать, что в переходный период такие детекторы
будут применяться наряду с фасетчатой коррекцией кривизны фокальной поверхности,
как это было сделано в космическом телескопе Kepler. Радиус кривизны фокальной
поверхности VT-119g равен 782 мм, так что в плоском детекторе с диагональю, скажем,
25 мм краевые изображения звезд размываются до 50 мкм. Предварительные расчеты
показывают, что качество изображений можно существенно улучшить при помощи лишь
одной линзочки, сделанной из плавленого кварца, и полностью восстановить дублетом из
того же материала. Фактически достаточно изменить форму входного окна перед плоским
приемником света.
Что касается экранирования света приемником, расположенным между линзовым
корректором и зеркалом, то приходится, как и раньше, ограничиваться частью доступной
фокальной поверхности. Поскольку общая площадь детекторов остается достаточно
большой, а изображения объектов характеризуются высоким качеством, регистрация даже
узкой полосы неба размерами, скажем, 30°× 5° обеспечивает получение значительной
информации, тогда как доля экранированного света не превышает 7%.
Полезная особенность работы с частичным заполнением фокальной поверхности
состоит в том, что отдельные небольшие приемники света можно располагать
соответственно форме изучаемой области неба, причем как "в стык", так и раздельно.
9
Заключительные замечания
В новой системе диаметр поля зрения с высоким качеством изображений примерно
втрое превосходит ранее достигнутые значения, что соответствует увеличению площади
обзора на порядок величины. Вместе с тем при поле ~30° технологические ограничения
размеров линз дают для максимальной апертуры системы значение около 80 см, что
заметно уступает диаметру обзорных телескопов с гораздо меньшим полем. Однако поле
зрения размерами 30° - 50° требуется далеко не всегда, и тогда появляется возможность
заметно увеличить апертуру телескопа. Как обычно, в каждой задаче нужно оптимально
подбирать размеры апертуры и поля зрения телескопа наряду с выбором режима его
работы.
Поясним, о каких данных наблюдений может идти речь, обратившись к примеру,
когда наблюдения проводятся с описанным выше телескопом, а детекторы соответствуют
области неба площадью 30°× 5° = 150 кв. градусов (диаметр эквивалентного кругового
поля 13.8°). Предположим, что время экспозиции составляет 20 сек, а "мертвое время",
нужное для считывании данных и перенаведения телескопа на соседний участок неба,
равно 5 сек (реальное значение для современных роботизированных телескопов). В этом
случае скорость обзора неба составит 6 кв. градусов в секунду. Площадь видимой над
горизонтом небесной полусферы за вычетом непрозрачной полосы вокруг Млечного пути
и подсвеченной области вблизи горизонта равна по порядку величины 104 кв. градусов;
при указанных условиях она будет последовательно изучена за время около получаса.
Расчеты показывают, что предельная звездная величина такого обзора будет около 20m.
Глубину обзора можно улучшить, увеличив время экспозиции, но тогда снизится
скорость обзора. При необходимости можно воспользоваться более крупным телескопом с
полем зрения того же порядка. Так, качество изображений в системе с апертурой 50 см и
полем диаметром 45° мало уступает качеству, показанному на рис. 2. Один такой телескоп
полностью покрывает error box типичной вспышки в γ-диапазоне.
Очевидно, наиболее высокая эффективность обзора достигается при помощи
иерархической системы, состоящей из нескольких телескопов разного типа,
характеристики которых оптимально подобраны для решения общей задачи. Телескоп
описанного здесь типа мог бы служить базовым инструментом такой системы,
поставляющим исходную информацию для специализированных телескопов. Вполне
вероятно, что на этом пути будет получено эффективное решение проблемы астероидной
опасности и других задач, требующих чрезвычайно широкого поля зрения.
Среди областей возможных неастрономических применений новой оптической
системы в первую очередь привлекают внимание геофизика, исследования космических
лучей, спектроскопия и медицинская томография.

Я признателен Michel Boer (Recherche CNRS ARTEMIS, France), Roger Ceragioli
(University of Arizona, U.S.A.) и Yuri Petrunin (Telescope Engineering Company, U.S.A.) за
плодотворное обсуждение затронутых вопросов. Приношу также благодарность Walter
Stephani (Germany) и дирекции Hamburg Observatory за предоставление скана фотографии,
показанной на рис. 9 (оригинальный номер SS00000A − Wentorfer Muhle).
10
Литература
Общие сведения о телескопах приводятся в книгах:
Максутов Д.Д., Астрономическая оптика. М.-Л., Гостехиздат, 1946.
Михельсон Н.Н., Оптические телескопы. Теория и конструкция. М., Наука, 1976.
Rutten H.G.J., van Venrooij M.A.M., Telescope Optics. Willmann-Bell, Richmond, 1999.
Schroeder D.J., Astronomical Optics. Academic Press, San Diego, 2000 (Sec. ed.).
Теребиж В.Ю., Современные оптические телескопы. М., Наука, 2005;
гл. II в сб. "Небо и телескоп", ред.-сост. В.Г. Сурдин, М., ФИЗМАТЛИТ, 2014.
Исторический обзор камеры Шмидта и предшествующих ей систем:
Busch W., Ceragioli R.C., Stephani W., Journal of Astronomical History and Heritage,
16(2), 107, 2013.
Обзор оптических систем современных широкоугольных телескопов:
Terebizh V.Yu., New designs of survey telescopes. Astronomische Nachrichten/
Astronomical Notes, v. 332, No. 7, 714 – 742, 2011.
Первая публикация с описанием новой системы:
Terebizh V.Yu., arXiv:1507.07110v1 [astro-ph.IM] 25Jul 2015.
Развернутое описание системы:
Terebizh V.Yu., Astronomische Nachrichten/Astronomical Notes, 2015, in press.
11