Касательные плоскости и дифференциалы

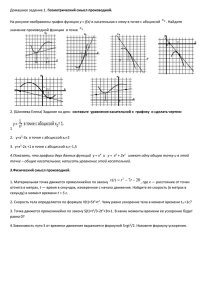
1
С.А. Лавренченко
www.lawrencenko.ru
Лекция 3
Касательные плоскости и дифференциалы
1. Касательные плоскости
Рис. 1.
Пусть поверхность S задана уравнением z  f ( x, y) , где функция f имеет
непрерывные первые частные производные. Пусть, далее, P( x0 , y0 , z 0 ) — точка на S .
Обозначим через C1 и C 2 сечения поверхности S вертикальными плоскостями y  y 0 и
x  x0 . Обозначим, далее через T1 и T2 касательные прямые к кривим C1 и C 2 в точке P .
Плоскость, проходящая через прямые T1 и T2 называется касательной плоскостью к
поверхности S в точке P . См рис. 1.
Выведем уравнение касательной плоскости. Как известно из курса аналитической
геометрии, любая плоскость, проходящая через точку P( x0 , y0 , z 0 ) имеет уравнение вида
A( x  x0 )  B( y  y0 )  C ( z  z 0 )  0 .
Поделим обе части уравнения на C . Обозначим  A C через k1 , и  B C через k 2 . Тогда
уравнение переписывается в форме:
(1)
z  z 0  k1 ( x  x0 )  k 2 ( y  y0 ) .
Если это уравнение задает касательную плоскость в точке P , то пересечение с
плоскостью y  y 0 задает касательную прямую T1 . Полагая y  y 0 в уравнении (1),
имеем:
z  z 0  k1 ( x  x0 )
y  y0
Мы узнаем уравнение прямой с угловым коэффициентом k1 . Этот угловой коэффициент
касательной T1 выражается частной производной f x( x0 , y0 ) , потому что переменная y
зафиксирована. Таким образом, k1  f x ( x0 , y 0 ) .
Аналогично, подставляя в (1) x  x0 , получаем z  z 0  k 2 ( y  y 0 ) — уравнение
касательной прямой T2 , поэтому k 2  f y ( x0 , y 0 ) .
Итак, мы вывели уравнение касательной плоскости к поверхности z  f ( x, y) в точке
P( x 0 , y 0 , z 0 ) :
2
(2)
z  z 0  f x( x0 , y 0 )( x  x0 )  f y ( x0 , y 0 )( y  y0 )
Пример 1.1. Найти уравнение касательной плоскости к эллиптическому параболоиду
z  2 x 2  y 2 в точке (1, 1, 3) .
Решение: Положим f ( x, y)  2 x 2  y 2 . Тогда
f x ( x, y )  4 x
f y ( x, y )  2 y
f x(1, 1)  4
f y (1, 1)  2
Подставляя в (2), получаем искомое уравнение:
z  3  4( x  1)  2( y  1)
или
z  4x  2 y  3 . ■
2. Понятие дифференцируемости
Для функции одной переменной y  f (x) , приращение функции в точке a определяется
следующим образом (см. Лекция 6, 1-й семестр):
y  f (a  x)  f (a) ,
где x  x  a — приращение независимой переменной. Если f дифференцируема в
точке a , то
(3)
y  f (a)x   x ,
где   0 при x  0 .
Рассмотрим сейчас функцию двух переменных z  f ( x, y) . Пусть x изменяется от a до
a  x и пусть y изменяется от b до b  y . Тогда соответствующее приращение
функции z равно
z  f (a  x, b  y)  f (a, b) .
По аналогии с (3), определим понятие дифференцируемости функции двух переменных
следующим образом.
Определение 2.1 (дифференцируемости). Функция z  f ( x, y) называется
дифференцируемой в точке (a, b) , если приращение функции z может быть
представлено в виде
(4)
 z  f x(a, b)x  f y (a, b)y   1 x   2 y ,
3
где  1  0 и  2  0 при (x, y)  (0, 0) .
Чтобы лучше понять это определение, потребуется понятие линеаризации. Мы знаем из
(2), что уравнение касательной плоскости к графику функции f ( x, y) в точке
(a, b, f (a, b)) имеет вид:
z  f (a, b)  f x(a, b)( x  a)  f y (a, b)( y  b) .
Линейная функция, L( x, y) , графиком которой является эта касательная плоскость,
называется линеаризацией функции f ( x, y) в точке (a, b) . Другими словами,
(5)
L( x, y)  f (a, b)  f x (a, b)( x  a)  f y (a, b)( y  b)
Смысл дифференцируемости состоит в том, что вблизи точки (a, b) функция f ( x, y)
приближенно равна ее линеаризации в этой точке:
(6)
f ( x, y)  L( x, y) ,
причем эта аппроксимация тем точнее, чем ближе точка ( x, y) к точке (a, b) .
Аппроксимация (6) называется линейной аппроксимацией функции f в точке (a, b) . В
геометрических терминах, касательная плоскость хорошо приближается к графику
функции f вблизи точки касания.
Иногда затруднительно проверить дифференцируемость функции непосредственно по
определению 2.1. Следующая теорема дает удобные достаточные условия для
дифференцируемости.
Теорема 2.2. Функция f ( x, y) дифференцируема в точке (a, b) , если частные
производные f x(a, b) и f y (a, b) существуют в некоторой окрестности точки (a, b) и
непрерывны в самой точке (a, b) . ■
Пример 2.3. Показать, что функция f ( x, y )  xe xy дифференцируема в (1, 0) и найти ее
линеаризацию в этой точке. Использовать найденную линеаризацию для приближенного
вычисления f (1.1, 0.1) .
Решение: Вычислим частные производные:
f x ( x, y)  e xy  xye xy
f y ( x, y )  x 2 e xy
f x(1, 0)  1
f y (1, 0)  1
Поскольку f x и f y — непрерывные функции, функция f дифференцируема, по теореме
2.2. Находим линеаризацию:
L( x, y)  f (1, 0)  f x(1, 0)( x  1)  f y (1, 0)( y  0)  1  1( x  1)  1  y  x  y ,
и соответствующую линейную аппроксимацию:
xe xy  x  y ,
4
откуда
f (1.1, 0.1)  1.1  0.1  1 .
Сравним полученную аппроксимацию с настоящим значением
f (1.1, 0.1)  1.1  e 0.11  0.98542 . ■
3. Дифференциалы
Вспомним (практическое занятие 9, 1-й семестр), что для функции одной переменной
y  f (x) ее дифференциал определяется как выражение вида
(7)
dy  f ( x) dx .
Дифференциал dx независимой переменной рассматривался тоже как независимая
переменная, которой можно придавать любые значения. Если независимым переменным
x и dx присвоить какие-нибудь конкретные значения x  a и dx  x  x  a , то разность
dy  y выражает величину зазора между касательной и кривой, образующегося при
сдвиге из a на величину x . Аппроксимация dy  y тем точнее, чем меньше x .
Для функции двух переменных z  f ( x, y) дифференциалы dx и dy определяются как
независимые переменные, которым можно присваивать любые конкретные значения.
Тогда дифференциал dz , также называемый полным дифференциалом, определяется как
выражение вида:
(8)
dz  f x ( x, y )dx  f y ( x, y )dy 
z
z
dx 
dy .
x
y
(Сравните с (7).) Придадим независимым переменным x и y произвольные значения:
x  a , y  b . Тогда дифференциал становится линейной функцией от переменных dx и
dy :
dz  f x(a, b)dx  f y (a, b)dy
Если теперь присвоить конкретные значения переменным dx и dy :
dx  x  x  a ,
dy  y  y  b ,
то
dz  f x(a, b)( x  a)  f y (a, b)( y  b) ,
и мы можем переписать линейную аппроксимацию (6) в терминах дифференциалов:
f ( x, y)  f (a, b)  dz
или
z  dz .
5
В геометрических терминах, разность dz  z выражает, величину зазора между
касательной плоскостью и поверхностью, образующегося при сдвиге из точки (a, b) в
точку (a  x, b  y ) . Заметим, что z  dz , но dz легче вычислять.
Пример 3.1.
(а) Найти дифференциал dz функции z  f ( x, y)  x 2  3xy  y 2 .
(б) Сравнить значения z и dz при изменении икса от 2 до 2.05 , а игрека от 3 до 2.96 .
Решение:
(а) Находим дифференциал по определению (7):
dz 
z
z
dx 
dy  (2 x  3 y )dx  (3x  2 y )dy .
x
y
(б) Подставляя x  2 , dx  x  0.05 , y  3 и dy  y  0.04 , вычисляем:
dz  (2  2  3  3)  0.05  (3  2  2  3)  (0.04)  0.65 .
Вычисляем приращение z :
z  f (2.05, 2.96)  f (2, 3)

 
 (2.05) 2  3  (2.05)  (2.96)  (2.96) 2  2 2  3  2  3  32
 0.6449 . ■

4. Функции трех и большего числа переменных
Линеаризация, дифференцируемость и дифференциалы определяются аналогично для
функций более двух переменных. Линеаризация функции трех переменных w  f ( x, y, z )
в точке (a, b, c) определяется так:
L( x, y, z )  f (a, b, c)  f x (a, b, c)( x  a)  f y (a, b, c)( y  b)  f z(a, b, c)( z  c) .
(Сравните с (5).) Линейная аппроксимация для функций трех переменных w  f ( x, y, z )
записывается так:
f ( x, y, z )  L( x, y, z ) .
(Сравните с (5).) Приращение w определяется так:
w  f ( x  x, y  y, z  z )  f ( x, y, z ) .
Наконец, дифференциал dw определяется в терминах дифференциалов dw , dw и dw
независимых переменных следующим образом:
6
dw 
w
w
w
dx 
dy 
dz .
x
y
z