Определить положение центра тяжести диска, в котором

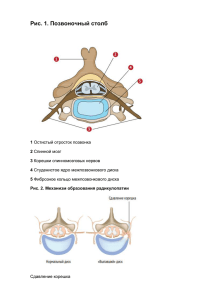
Определить положение центра тяжести диска, в котором сделаны
два круговых «выреза». Радиусы круговых вырезов равны половине и
четверти радиуса диска. Центры вырезов находятся на линии
одного из диаметров по разные стороны от центра диска.
Расстояния от центра диска до центров каждого из вырезов равны
половине радиуса диска. Радиус диска равен 44 см.
На рисунке показан диск с вырезами, радиусы которых равны ⁄2 и
⁄4, в выбранной системе координат. Начало координат совпадает с
центром диска, центры вырезов расположены на оси по обе стороны
от центра.
Произведем расчет положения центра
тяжести диска с вырезами по алгоритму.
1. Рассмотрим диск и вырезы как
несколько фигур правильной формы.
Диск и вырезы являются фигурами
правильной формы; центры фигур
(кругов) совпадают с центрами их
тяжести. Конфигурация расположения
центров диска и вырезов является
линейной. Расстояние от центра диска до центра тяжести конструкции
совпадает с x-координатой центра тяжести и задается формулой:
с ,
где – координата центра диска массой (точка ), – координата
центра выреза массой (точка ), – координата центра выреза
массой (точка ).
2. Запишем координаты центров тяжести (центров масс) каждого из
тел:
для диска радиусом –
0,
для выреза радиусом ⁄4 –
⁄2,
для выреза радиусом ⁄2 –
⁄2.
3. Определим массы каждого из тел, считая тела плоскими фигурами:
для диска радиусом –
ρ ,
для выреза радиусом ⁄4 –
ρ ⁄4 ,
для выреза радиусом ⁄2 –
ρ ⁄2 ,
где ρ – плотность диска, – плотность вырезов, – площадь
диска, ⁄4 – площадь выреза радиусом ⁄4, ⁄2 –
площадь выреза радиусом ⁄2.
4. Рассчитаем координату центра тяжести диска с вырезами. Для этого
подставим массы и координаты каждой из фигур в исходную
формулу:
∙ 0 ⁄4 ∙ ⁄2 ⁄2 ∙ ⁄2
.
⁄4 ⁄2 После преобразования формулы получим:
3 3 ∙ 44
с 6,0см.
22
22
Таким образом, центр тяжести диска с вырезами расположен на линии,
соединяющей центры диска и вырезов, и находится на расстоянии 6,0
см от центра диска.