3.19. Объем шара
advertisement
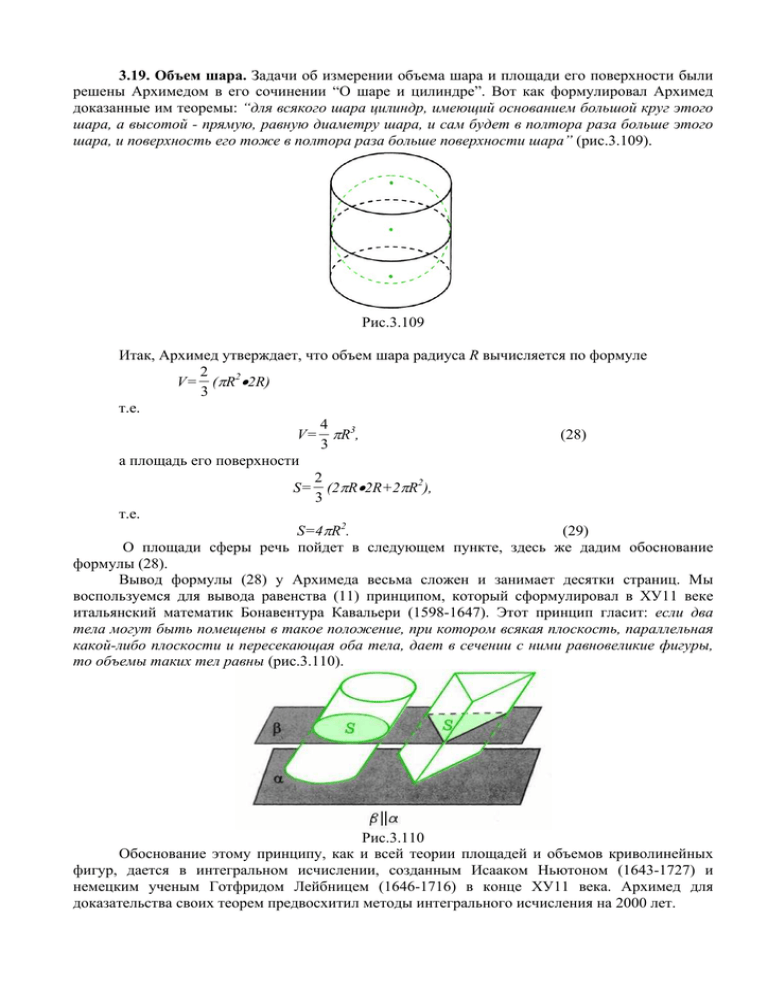
3.19. Объем шара. Задачи об измерении объема шара и площади его поверхности были решены Архимедом в его сочинении “О шаре и цилиндре”. Вот как формулировал Архимед доказанные им теоремы: “для всякого шара цилиндр, имеющий основанием большой круг этого шара, а высотой - прямую, равную диаметру шара, и сам будет в полтора раза больше этого шара, и поверхность его тоже в полтора раза больше поверхности шара” (рис.3.109). Рис.3.109 Итак, Архимед утверждает, что объем шара радиуса R вычисляется по формуле 2 V= (πR2•2R) 3 т.е. 4 V= πR3, (28) 3 а площадь его поверхности 2 S= (2πR•2R+2πR2), 3 т.е. S=4πR2. (29) О площади сферы речь пойдет в следующем пункте, здесь же дадим обоснование формулы (28). Вывод формулы (28) у Архимеда весьма сложен и занимает десятки страниц. Мы воспользуемся для вывода равенства (11) принципом, который сформулировал в ХУ11 веке итальянский математик Бонавентура Кавальери (1598-1647). Этот принцип гласит: если два тела могут быть помещены в такое положение, при котором всякая плоскость, параллельная какой-либо плоскости и пересекающая оба тела, дает в сечении с ними равновеликие фигуры, то объемы таких тел равны (рис.3.110). Рис.3.110 Обоснование этому принципу, как и всей теории площадей и объемов криволинейных фигур, дается в интегральном исчислении, созданным Исааком Ньютоном (1643-1727) и немецким ученым Готфридом Лейбницем (1646-1716) в конце ХУ11 века. Архимед для доказательства своих теорем предвосхитил методы интегрального исчисления на 2000 лет. Архимед очень гордился этими открытиями и по его воле на его могильной плите был изображен цилиндр с вписанным шаром, а эпитафия гласила, что их объемы относятся как 3:2. Опираясь на принцип Кавальери, можно утверждать, что объем шара радиуса R равен оставшийся части цилиндра С с высотой 2R и радиусом основания R, из которого удалили два конуса, изображенные на рисунке 3.111. Рис.3.111 Действительно, площади заштрихованных сечений (круга и кольца), как нетрудно подсчитать, равны. Поэтому объем V шара радиуса R равен объему цилиндра С без удвоенного объема конуса с высотой R и радиусом основания также R, т.е. 2 2 4 πR •R= πR3. 3 3 Равенство (28) установлено. V= πR2•2R - Вопросы для самоконтроля 1. Кто и когда вычислил объем шара? 2. Используя какой принцип, мы вычислили объем шара? Задачи Работаем с формулой. 19.1. Как изменился объем шара, когда его радиус: а) увеличился в два раза; б) уменьшился в три раза? 19.2. Как изменить радиус шара, чтобы: а) его объем увеличился в 2 раза; б) уменьшился в 5 раз? Вычисляем. 19.3. Какую часть объема куба составляет объем вписанного в него шара? (У) 19.4. Какую часть от объема шара составляет объем вписанного в него куба? (У) 19.5. Какую часть от объема шара составляет объем вписанного в него: а) цилиндра, имеющего своим осевым сечением квадрат; б) конуса, имеющего своим осевым сечением равнобедренный прямоугольный треугольник; в) конуса, имеющего своим осевым сечением равносторонний треугольник? (У) Оцениваем. 19.6. Из сплошного металлического шара радиусом 20 см выплавили шарики радиусом 1 см. Сколько их получилось? 19.7. Какая часть объема шара радиуса R содержится между его сферой и концентрической и нею сферой радиуса 0,9R? 19.8. Из сплошного металлического шара радиуса R изготовили полый шар, толщина стенок которого 0,1R. Каков его радиус (внешний)? (У) Применяем геометрию. 19.9. Что бы вы предпочли: съесть арбуз радиуса 15 см вчетвером или съесть арбуз радиуса 20 см ввосьмером? (Р) 19.10.Диаметр Земли приблизительно в четыре раза больше диаметра Луны. Сравните объемы Земли и Луны, считая их шарами. (Р)


