Релаксационные генераторы с триггером Шмидта

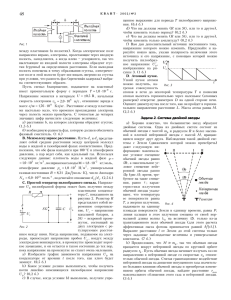
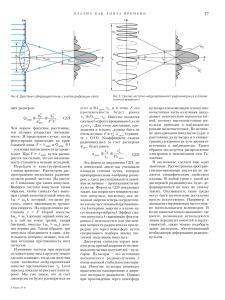
Ðåëàêñàöèîííûå ãåíåðàòîðû
ñ òðèããåðîì Øìèäòà
Îòëè÷èòåëüíîé îñîáåííîñòüþ ýëåêòðîííîé ñõåìû ñ íàçâàíèåì
«òðèããåð Øìèäòà» ÿâëÿåòñÿ íàëè÷èå ïåòëè ãèñòåðåçèñà â ïåðåäàòî÷íîé õàðàêòåðèñòèêå, òî åñòü çàâèñèìîñòè âûõîäíîãî ñèãíàëà
îò âõîäíîãî (ðèñ.1).
Ò
àêàÿ õàðàêòåðèñòèêà ïîëó÷àåòñÿ,
åñëè óñèëèòåëü îõâàòèòü öåïüþ
ãàëüâàíè÷åñêîé ïîëîæèòåëüíîé
îáðàòíîé ñâÿçè. Èçâåñòíû ñõåìû òðèããåðà Øìèäòà íà ýëåêòðîííûõ ëàìïàõ,
ïîëåâûõ è áèïîëÿðíûõ òðàíçèñòîðàõ è
â èíòåãðàëüíîì èñïîëíåíèè. Â äàííîé
ñòàòüå áóäåò ðàññìîòðåíà ñõåìà òðèããåðà Øìèäòà íà îïåðàöèîííîì óñèëèòåëå (ðèñ. 2), ïîçâîëÿþùàÿ â ðÿäå ñëó÷àåâ ïîëó÷èòü ïðè åå ïðèìåíåíèè èíòåðåñíûå ðåçóëüòàòû.
UВЫХ
UВХ
Ðèñ. 1
Ðàññìàòðèâàåìàÿ ñõåìà èìååò ñèììåòðè÷íóþ ïåòëþ ãèñòåðåçèñà (ðèñ. 3),
ïðè óñëîâèè,
UВХ
÷òî íàïðÿæåUВЫХ
íèå íàñûùåíèå Uí îïåðàR2
öèîííîãî
R1
óñèëèòåëÿ â
îáëàñòè ïîëîÐèñ. 2
æèòåëüíîãî è
îòðèöàòåëüíîãî âûõîäíîãî
UВЫХ
íàïðÿæåíèÿ
êîëè÷åñòâåííî
UH
–UП
îäèíàêîâû, ÷òî
UВХ
÷àùå âñåãî è
–UH
UП
íàáëþäàåòñÿ.
Øèðèíà ïåòëè
ã è ñ ò å ð åç è ñ à
Ðèñ. 3
îïðåäåëÿåòñÿ
âåëè÷èíîé ïîðîãîâûõ íàïðÿæåíèé, çàâèñÿùèõ îò ñîîòíîøåíèÿ ñîïðîòèâëåíèé
ðåçèñòîðîâ R1 è R2:
Uï = Uí ⋅ R1/(R1+R2).
Íàèáîëåå ÷àñòî òðèããåð Øìèäòà èñïîëüçóåòñÿ â êà÷åñòâå ïîðîãîâîãî óñòðîéñòâà ñ óìåíüøåííîé ÷óâñòâèòåëüíîñòüþ ê ñèãíàëàì ïîìåõ. Îäíàêî â
äàííîé ñòàòüå áóäóò ðàññìîòðåíû äðóãèå åãî ïðèìåíåíèÿ.
Ãåíåðàòîð ïðÿìîóãîëüíîãî
íàïðÿæåíèÿ
Ñõåìà ãåíåðàòîðà ñ ñèãíàëîì ïðÿìîóãîëüíîé ôîðìû, î÷åíü áëèçêèì ê ìåàíäðó, èçîáðàæåíà íà ðèñ. 4. Çäåñü èíòåãðèðóþùàÿ RC-öåïî÷êà ñòîèò â öåïè
îòðèöàòåëüíîé îáðàòíîé ñâÿçè. Íàïðÿæåíèå ïðÿìîóR
ãîëüíîé ôîðìû íà
C
âûõîäå ñõåìû èíòåãðèðóåòñÿ ýòîé öåïî÷êîé è íà èíâåðòèðóþùåì âõîäå ÎÓ
R2
R1
ïîëó÷àåòñÿ ïèëîîáðàçíîå íàïðÿæåíèå,
ñîñòîÿùåå èç îòðåçÐèñ. 4
êîâ ýêñïîíåíò ñ àìïëèòóäîé ðàâíîé ïîðîãîâîìó íàïðÿæåíèþ òðèããåðà Øìèäòà.
Ýòîò ñèãíàë ïåðåêëþ÷àåò òðèããåð ïî ïåòëå ãèñòåðåçèñà. Àíàëèç ñõåìû ãåíåðàòîðà ïîêàçûâàåò, ÷òî ÷àñòîòà ãåíåðàöèè
îïðåäåëÿåòñÿ âûðàæåíèåì
2R1
VT2
R2
Ò+= R+ ⋅ C ⋅ ln(1+2R1/R2)
T–= R– ⋅ C ⋅ ln(1+2R1/R2).
Ïîñêîëüêó õàðàêòåðèñòèêè
äèîäîâ çàìåòíî
R–
çàâèñÿò îò òåìïåðàòóðû, òåìÐèñ. 5
ïåðàòóðíàÿ ñòàáèëüíîñòü
÷àñòîòû ãåíåðèðóåìîãî ñèãíàëà íåñêîëüêî óõóäøèòñÿ.
R+
Ãåíåðàòîðû ëèíåéíî
ìåíÿþùåãîñÿ íàïðÿæåíèÿ
 ñõåìå íà ðèñ. 6 êîíäåíñàòîð áûñòðî çàðÿæàåòñÿ ÷åðåç ýìèòòåðíûé ïîâòîðèòåëü íà òðàíçèñòîðå VÒ1 è ìåäëåííî
R3
R2
R1
C
–UП
Ðèñ. 6
ðàçðÿæàåòñÿ ïîñòîÿííûì
òîêîì, âûðàáàòûâàåìûì
ñõåìîé íà òðàíçèñòîðå VÒ2.
 ðåçóëüòàòå íà êîíäåíñàòîðå ïîëó÷àåòñÿ ïèëîîáðàçíîå ëèíåéíî ïàäàþùåå
íàïðÿæåíèå. Ïðè R1 = R2
÷àñòîòà ãåíåðàöèè áóäåò â
ïåðâîì ïðèáëèæåíèè îïðåäåëÿòüñÿ âûðàæåíèåì
+UП
DA1
544УД2
C1
10,0
R3
7,5 к
VT1
KT815
DA2
544УД2
RH
L
20 мкГн
R8
100
R4
12 к
R2
1,3 к
R7
8,2
C3
0,47
VT2
KT814
–UП
Äëÿ òîãî, ÷òîáû ôîðìà Ðèñ. 8
ãåíåðèðóåìîãî ñèãíàëà íå
èñêàæàëàñü, íàãðóçêà ãåíåðàòîðà äîëæíà èìåòü äîñòàòî÷íî áîëüøîå ñîïðîòèâëåíèå, ëèáî íåîáõîäèìî èñïîëüçîâàòü äîïîëíèòåëüíûé áóôåðíûé
R2
R1
R
R5
15 к
R6
8,2
C2 75
R1
1,3 к
f = 1/(3 ⋅ R3 ⋅ C).
f = 1/(2 ⋅ R ⋅ C ⋅ ln(1+2R1/R2)).
Ýòîò ðåçóëüòàò íå çàâèñèò îò íàïðÿæåíèÿ ïèòàíèÿ ÎÓ è íàïðÿæåíèÿ íàñûùåíèÿ.  ðåçóëüòàòå ñòàáèëüíîñòü ÷àñòîòû
ãåíåðàöèè ïîëó÷àåòñÿ íàìíîãî áîëåå âûñîêîé â ñðàâíåíèè ñ äðóãèìè ðåëàêñàöèîííûìè ãåíåðàòîðàìè. Ïî ñóùåñòâó íåñòàáèëüíîñòü ÷àñòîòû ãåíåðàöèè, åñëè
îíà íå ñëèøêîì âûñîêà, îïðåäåëÿåòñÿ
íåñòàáèëüíîñòüþ ýëåìåíòîâ R, C, R1 è
R2 â ñîîòâåòñòâèè ñ ïðèâåäåííîé âûøå
ôîðìóëîé.  äèàïàçîíå çâóêîâûõ ÷àñòîò
êðàòêîâðåìåííàÿ íåñòàáèëüíîñòü ÷àñòîòû ìîæåò áûòü ìåíüøå ÷åì 0,01%.
Çàìåíèâ R íà öåïî÷êó, ïîêàçàííóþ íà
ðèñ. 5, ïîëó÷èì âîçìîæíîñòü ãåíåðèðîâàòü íåñèììåòðè÷íûé ñèãíàë ïðÿìîóãîëüíîé ôîðìû ñ íåçàâèñèìîé ðåãóëèðîâêîé äëèòåëüíîñòè ïîëîæèòåëüíîé è
îòðèöàòåëüíîé ïîëóâîëí.
åñëè íà ïåðâîå ìåñòî âûõîäÿò òðåáîâàíèÿ êîìïàêòíîñòè è âûñîêîãî êîýôôèöèåíòà ïîëåçíîãî äåéñòâèÿ, èñïîëüçîâàíèå
óñèëèòåëÿ êëàññà “D” ìîæåò îêàçàòüñÿ îïðàâäàííûì. Ñõåìà òàêîãî óñèëèòåëÿ
èçîáðàæåíà íà ðèñ. 8.
Ìîäóëÿòîð ØÈÌ èñïîëüçóåò ýëåêòðîííûé èíòåãðàòîð DA1 è òðèããåð
Øìèäòà DA2, îáðàçóþùèå ãåíåðàòîð
ïðÿìîóãîëüíîãî íàïðÿæåíèÿ. Âõîäíîé
ñèãíàë ìîäóëèðóåò èìïóëüñû ïî øèðè-
+UП
VT1
C
Ðèñ. 7
óñèëèòåëü ñ áîëüøèì âõîäíûì ñîïðîòèâëåíèåì. Â ñõåìå íà ðèñ. 7 èñïîëüçóåòñÿ äðóãîé âàðèàíò ïîñòðîåíèÿ òðèããåðà Øìèäòà.
Ñèãíàë ñíèìàåòñÿ ñ âûõîäà ýëåêòðîííîãî èíòåãðàòîðà, èìåþùåãî íèçêîå âûõîäíîå ñîïðîòèâëåíèå, ÷òî óïðîùàåò
ñîãëàñîâàíèå ñ íèçêîîìíîé íàãðóçêîé.
Ïîðîãîâûå íàïðÿæåíèÿ ïåòëè ãèñòåðåçèñà ðàâíû Uï = UíR1/R2. ×àñòîòà ãåíåðàöèè îïðåäåëÿåòñÿ ôîðìóëîé
f = R2/(2 ⋅ R ⋅ C ⋅ R1).
íå èìåííî òàê, êàê íàäî äëÿ ðàáîòû
óñèëèòåëÿ êëàññà “D”. Ïîëó÷åííûå èìïóëüñû óñèëèâàþòñÿ ïî òîêó òðàíçèñòîðàìè VT1 è VT2 è ÷åðåç óñðåäíÿþùóþ öåïî÷êó L, C3 ïîäàþòñÿ â íàãðóçêó.
Âñÿ ñõåìà îõâà÷åíà öåïüþ îòðèöàòåëüíîé îáðàòíîé ñâÿçè ÷åðåç ðåçèñòîð R2.
×àñòîòà òàêòîâûõ èìïóëüñîâ ØÈÌ-ãåíåðàòîðà îêîëî 300 êÃö.  äèàïàçîíå
çâóêîâûõ ÷àñòîò êîýôôèöèåíò íåëèíåéíûõ èñêàæåíèé îêîëî 0,1%.  ïðèâåäåííîé ñõåìå èñïîëüçîâàí ïðîñòåéøèé âûõîäíîé óñèëèòåëü, íå îáåñïå÷èâàþùèé
ïîëó÷åíèå ìàêñèìàëüíîãî êîýôôèöèåíòà ïîëåçíîãî äåéñòâèÿ, íî äîñòàòî÷íûé äëÿ èëëþñòðàöèè ïðèíöèïà äåéñòâèÿ óñèëèòåëÿ êëàññà “D”.
Øèðîòíî-èìïóëüñíûé ìîäóëÿòîð óñòðîéñòâà, ïðèâåäåííîãî íà ðèñ. 8, ìîæåò áûòü ïðèìåíåí â óñòðîéñòâàõ ìàãíèòîôîííîé çàïèñè. Åãî âûõîäíîé
ñèãíàë ñîäåðæèò âñå íåîáõîäèìûå êîìïîíåíòû äëÿ íåïîñðåäñòâåííîé ïîäà÷è åãî íà çàïèñûâàþùóþ ìàãíèòîôîííóþ ãîëîâêó. Îòïàäàåò íåîáõîäèìîñòü
â ïðèìåíåíèè äîïîëíèòåëüíîãî ãåíåðàòîðà ïîäìàãíè÷èâàíèÿ.
Ãåîðãèé Ïåòèí
[email protected]
Åñëè âûáðàòü R2 = 2R1, òîãäà f =
1/(RC).
Óñèëèòåëü êëàññà “D”
Ýòî óñèëèòåëü, â êîòîðîì ñèãíàë ïðåîáðàçóåòñÿ â øèðîòíî-èìïóëüñíî ìîäóëèðîâàííûé ñèãíàë (ØÈÌ), ñ ïîñëåäóþùèì âîññòàíîâëåíèåì èñõîäíîãî ñèãíàëà
ïîñðåäñòâîì èñïîëüçîâàíèÿ óñðåäíÿþùåé öåïî÷êè. Ïîñêîëüêó ïðè óñèëåíèè
èñïîëüçóþòñÿ èìïóëüñû ïðÿìîóãîëüíîé
ôîðìû, è óñèëèòåëüíûå ýëåìåíòû ðàáîòàþò â êëþ÷åâîì ðåæèìå, òåîðåòè÷åñêèé
êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ òàêîãî óñèëèòåëÿ ðàâåí 100%. Íåäîñòàòêàìè
óñèëèòåëÿ êëàññà “D” ÿâëÿþòñÿ áîëåå
ñëîæíàÿ ñõåìà, ïîâûøåííûé óðîâåíü
øóìîâ è ñîçäàíèå ðàäèîïîìåõ. Îäíàêî
Ëèòåðàòóðà
1. Ïåòèí Ã. Ï. Ðåëàêñàöèîííûå ãåíåðàòîðû è ðåëàêñàöèîííûå ðåëå ñ èñïîëüçîâàíèåì ñõåìû ñëåäÿùåãî ðåëå. — Ðàäèîòåõíèêà, 1958, ¹7.
2. Ïåòèí Ã. Ï. Òðèããåð Øìèäòà íà ïëîñêîñòíûõ òðèîäàõ. — Ðàäèîòåõíèêà, 1959,
¹9.
3. Àëåêñåíêî À. Ã., Êîëîìáåò Å. À., Ñòàðîäóá Ã. È. Ïðèìåíåíèå ïðåöèçèîííûõ àíàëîãîâûõ ìèêðîñõåì. — Ì.: Ðàäèî è ñâÿçü.
1985.
4. Êîëîìáåò Å. À. Ìèêðîýëåêòðîííûå
ñðåäñòâà îáðàáîòêè àíàëîãîâûõ ñèãíàëîâ. — Ì.: Ðàäèî è ñâÿçü, 1991.
5. Òèòöå Ó., Øåíê Ê. Ïîëóïðîâîäíèêîâàÿ
ñõåìîòåõíèêà. — Ì.: Ìèð, 1982.
6. Õîðîâèö Ï., Õèëë Ó. Èñêóññòâî ñõåìîòåõíèêè. — Ì.: Ìèð. 1993.