О СТАБИЛИЗАЦИИ СЖАТИЯ ЛАЙНЕРА

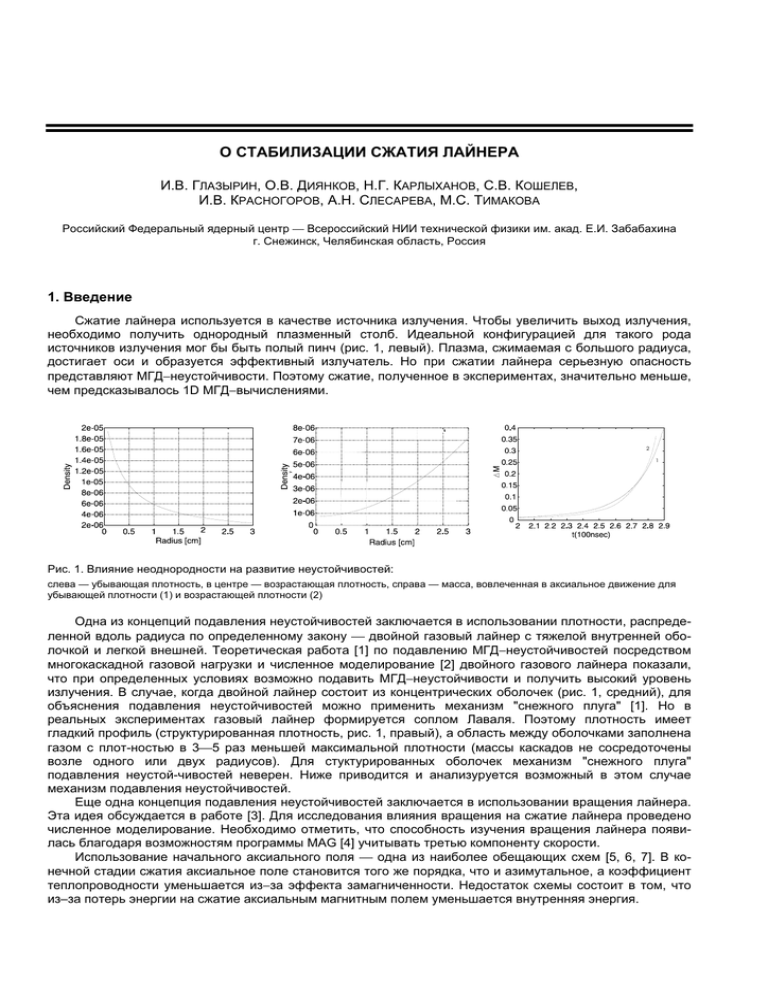
О СТАБИЛИЗАЦИИ СЖАТИЯ ЛАЙНЕРА
И.В. ГЛАЗЫРИН, О.В. ДИЯНКОВ, Н.Г. КАРЛЫХАНОВ, С.В. КОШЕЛЕВ,
И.В. КРАСНОГОРОВ, А.Н. СЛЕСАРЕВА, М.С. ТИМАКОВА
Российский Федеральный ядерный центр  Всероссийский НИИ технической физики им. акад. Е.И. Забабахина
г. Снежинск, Челябинская область, Россия
1. Введение
Сжатие лайнера используется в качестве источника излучения. Чтобы увеличить выход излучения,
необходимо получить однородный плазменный столб. Идеальной конфигурацией для такого рода
источников излучения мог бы быть полый пинч (рис. 1, левый). Плазма, сжимаемая с большого радиуса,
достигает оси и образуется эффективный излучатель. Но при сжатии лайнера серьезную опасность
представляют МГД−неустойчивости. Поэтому сжатие, полученное в экспериментах, значительно меньше,
чем предсказывалось 1D МГД−вычислениями.
2
1
Рис. 1. Влияние неоднородности на развитие неустойчивостей:
слева — убывающая плотность, в центре — возрастающая плотность, справа — масса, вовлеченная в аксиальное движение для
убывающей плотности (1) и возрастающей плотности (2)
Одна из концепций подавления неустойчивостей заключается в использовании плотности, распределенной вдоль радиуса по определенному закону  двойной газовый лайнер с тяжелой внутренней оболочкой и легкой внешней. Теоретическая работа [1] по подавлению МГД−неустойчивостей посредством
многокаскадной газовой нагрузки и численное моделирование [2] двойного газового лайнера показали,
что при определенных условиях возможно подавить МГД−неустойчивости и получить высокий уровень
излучения. В случае, когда двойной лайнер состоит из концентрических оболочек (рис. 1, средний), для
объяснения подавления неустойчивостей можно применить механизм "снежного плуга" [1]. Но в
реальных экспериментах газовый лайнер формируется соплом Лаваля. Поэтому плотность имеет
гладкий профиль (структурированная плотность, рис. 1, правый), а область между оболочками заполнена
газом с плот-ностью в 35 раз меньшей максимальной плотности (массы каскадов не сосредоточены
возле одного или двух радиусов). Для стуктурированных оболочек механизм "снежного плуга"
подавления неустой-чивостей неверен. Ниже приводится и анализуруется возможный в этом случае
механизм подавления неустойчивостей.
Еще одна концепция подавления неустойчивостей заключается в использовании вращения лайнера.
Эта идея обсуждается в работе [3]. Для исследования влияния вращения на сжатие лайнера проведено
численное моделирование. Необходимо отметить, что способность изучения вращения лайнера появилась благодаря возможностям программы MAG [4] учитывать третью компоненту скорости.
Использование начального аксиального поля  одна из наиболее обещающих схем [5, 6, 7]. В конечной стадии сжатия аксиальное поле становится того же порядка, что и азимутальное, а коэффициент
теплопроводности уменьшается из−за эффекта замагниченности. Недостаток схемы состоит в том, что
из–за потерь энергии на сжатие аксиальным магнитным полем уменьшается внутренняя энергия.
О стабилизации сжатия лайнера
379
Конфигурация лайнера и форма тока во всех приведенных выше подходах к изучению подавления
неустойчивости брались из экспериментов, проводимых в HCEI, Томск [8]. Было сделано предположение
о распространении газа из сопла и определен начальный профиль плотности.
Чтобы проанализировать развитие неустойчивостей, в области максимальной плотности внешней
оболочки были заданы случайные возмущения Одна волна возмущения описывалась 10 точками
расчетной сетки. Таким образом, если расчетная сетка была 100 точек вдоль радиуса и 300 точек вдоль
оси z, можно наблюдать развитие неустойчивостей до 30 моды включительно. Величина возмущений
составляла 510% от величины плотности.
Система уравнений, используемая при моделировании, взята из работы С.Л. Брагинского [9].
Перенос излучения учитывается уравнением теплопроводности для фотонной температуры. Средний
заряд берется из таблицы коэффициентов, определенных столкновительно−радиационной моделью 1D
программы ЭРА [10]. Магнитное поле на границе сетки определяется из уравнения цепи. После этого ток
распределяется в соответствии с диффузией магнитного поля. Следует отметить, что в уравнении
магнитного поля не учитывались Холловский член и член, отвечающий за образование спонтанного
магнитного поля.
2. Структурированная нагрузка
Было сделано предположение, что сжатие стабилизируется, когда ударная волна проходит по
плотности, возрастающей к оси. Подавление неустойчивостей происходит из−за увеличения массы
сжимаемого газа. Возможное объяснение этого связано с движением волны через возрастающую
плотность. В результате ускорение границы плазма−магнитное поле уменьшается, что приводит к более
устойчивому сжатию. Можно провести аналогию с неустойчивостью Релей−Тейлора, если рассматривать
плазму в качестве легкой жидкости, а магнитное поле  в качестве тяжелой. Тяжелая жидкость давит на
легкую, развиваются неустойчивости. Чем плотнее легкая жидкость, тем устойчивее такая конфигурация.
В работе [11] подробно описан механизм подавления неустойчивостей в концентрических оболочках,
связанный с выравниванием давления вдоль поверхности внешней оболочки из−за прогрева ударной
волны. Эта ударная волна формируется во время удара внешней оболочки о внутреннюю. Как уже
упоминалось выше, для структурированных оболочек этот механизм неприменим.
Чтобы проанализировать предложенный выше механизм подавления неустойчивостей, рассматривались два профиля плотности: плотность менялась по закону 1/r и r**2, (r  радиальная координата).
Для оценки роста неустойчивости из работы [12] взята характеристика "доля массы, вовлеченной
в движение". Она показывает, какая часть массы лайнера вовлечена в аксиальное движение. Численное
моделирование показывает, что в первом случае доля вовлеченной массы растет быстрее, чем во
втором случае (рис. 1, правый). Возможно следующее объяснение этого явления. Ударная волна,
движимая магнитным давлением лайнера, встречает возрастающую плотность, ускорение границы
плазма−магнитное поле уменьшается, что приводит к более устойчивому сжатию.
Для количественной оценки роста неустойчивостей была введена мера "величина возмущений",
позволяющая определеть перерастание мелкомасштабных возмущений в крупномасштабные. Эта мера
орпеделялась следующим образом: вычисленное распределение плотности разлагалось в ряд Фурье.
Быстрый рост первых гармоник показывает доминирование крупномасштабных возмущений. Увеличение
амплитуд гармоник с высокими номерами говорит о росте мелкомасштабных возмущений. (Однородное
сжатие лайнера есть сжатие с крупномасштабными возмущениями.)
В случае двойного газового лайнера с тяжелой внутренней оболочкой и легкой внешней конфигурация становится неустойчивой после того, как ударная волна пройдет через первый пик плотности,
потому что волна начинает двигаться от тяжелого вещества к легкому (рис. 2, правый). При движении
волны по возрастающей плотности сжатие стабилизируется. Когда ударная волна пройдет второй пик
плотности, неустойчивости снова начинают расти. Но в целом такая конфигурация более устойчива, чем
в случае однородного или полого пинча. Выдвигается гипотеза, объясняющая большую устойчивость
структурированных оболочек. На рис. 2 приведены различные профили плотности. И в то же время рис.
2, левый показывает конфигурацию, которая может быть получена
• в начале сжатия полого пинча;
• при сжатии однородного столба по истечении некоторого времени;
• при сжатии любой газовой нагрузки, в том числе и двойного газового лайнера, перед моментом
максимального сжатия в случае, когда магнитное поле скинировано. Это предположение применимо
для рассматриваемых геометрий и форм тока. Эти три случая соответствуют
• началу развития неустойчивостей;
• промежуточной стадии развития;
• финальной стадии.
380
И.В. Глазырин, О.В. Диянков, Н.Г. Карлыханов и др.
На левом рис. 2 показано, что сжимается убывающая к оси плотность. Чем дольше по времени развивается неустойчивость, тем неустойчивей сжатие.
Рис. 2. Профили плотности:
слева  полый пинч, в центре  концентрические оболочки, справа  структурированные оболочки
Для изучения эффекта перерастания мелкомасштабных мод в крупномасштабные проведена серия
расчетов с отключением некоторых физических процессов, влияющих на развитие неустойчивостей.
Было выявлено, что теплопроводность играет здесь существенную роль. Результаты показаны на рис. 3.
В случае учета теплопроводности заметен переход к развитию крупномасштабных волн.
Рис. 3. Влияние теплопроводности на развитие неустойчивостей:
слева  расчет с учетом теплопроводности, справа  теплопроводность не учитывалась
3. Вращение лайнера
Чтобы аналитически оценить радиус сжатого лайнера, предполагается, что
градиент магнитного поля в скин−слое, составляющем половину или треть радиуса, постоянен;
центробежная сила пропорциональна плотности и квадрату угловой скорости;
вращательный момент должен сохраняться;
силы центробежного и магнитнго давлений должны быть равны.
Учитывая все выше сказанное, можно получить зависимость для минимального радиуса. Радиус
пропорционален угловой скорости и квадрату глубины скинирования. Среднее значение, вычисленное
для заданных параметров лайнера и генератора, близко к 1−D результатам.
1−D моделирование дало неожиданные результаты. Моделирование показало, что существует
оптимальная скорость вращения в смысле получения максимальной плотности. Для параметров лайнера
и электрической цепи, используемых в расчете, эта скорость равна 10 5 ceк −1 .
На рис. 4 представлено пространственное распределение температуры и плотности лайнера,
начальная скорость вращения которого равна 10 5 ceк −1 , и те же распределения для невращающегося
О стабилизации сжатия лайнера
381
лайнера. Легко заметить, что наиболее плотная часть вращающегося лайнера холодная, а область
внутри лайнера значительно горячее.
3
2
4
1
Рис. 4. Пространственное распределение характеристик лайнера:
1  плотность невращающегося лайнера, 2  температура невращающегося лайнера, 3  плотность вращающегося лайнера,
4  температура вращающегося лайнера
Целью 2D моделирования было выяснить, насколько стабильно сжатие вращающегося лайнера.
Опять были получены неожиданные результаты. Оказывается, что на стадии максимального сжатия
(максимальной плотности) во вращающемся лайнере все моды растут быстрее, чем в невращающемся
лайнере. Сжатие вычисленной вовлеченной массы для вращающегося и невращающегося лайнеров
показывает показывает опасный рост неустойчивостей в первом случае. Поэтому даже для оптимальной
скорости вращения ( 10 5 ceк −1 ) максимальная плотность много меньше, чем в 1D расчетах и равна
максимальной плотности для невращающегося лайнера.
Для анализа роста неустойчивостей использовалась методика, предложенная в работе [12], доля
массы вовлеченной в движение. На рис. 5 и 6 представлено пространственное распределение плотности
вращающегося и невращающегося лайнеров по результатам 2D расчетов. Видно, что в обоих случаях
плотная область состоит из нескольких плотных точек. Число точек зависит от начального
распределения плотности, но не превышает 10 точек на 2 см.
Рис. 5. Плотность в момент максимального сжатия
невращающегося лайнера
Рис. 6. Плотность в момент максимального сжатия
вращающегося лайнера
И.В. Глазырин, О.В. Диянков, Н.Г. Карлыханов и др.
382
4. Использование внешнего поля
Величина начального аксиального магнитного поля лайнера варьировалась от 0,5 до 5 кГс. Также
менялось распределения аксиального поля вдоль радиуса (рис. 711).
2
1
3
Рис. 7. Начальное распределение аксиального магнитного поля вдоль радиуса:
1  однородное поле вдоль радиуса, 2  поле сосредоточено между оболочками лайнера, 3  поле сосредоточено только во
внешней оболочке лайнера. Такое распределение поля близко к экспериментальному, когда внешняя оболочка предыонизуется
магнетронным разрядом [13]
1
2
3
3
2
1
Рис. 8. Внутренняя энергия:
Рис. 9. Магнитная энергия:
1  без аксиального поля, 2  поле 2 кГс сосредоточено между
оболочками, 3  аксиальное поле 2 кГс во внешней оболочке
1  без аксиального поля, 2  поле 2 кГс сосредоточено
между оболочками, 3  аксиальное поле 2 кГс во
внешней оболочке
1
2
1
3
2
Рис. 10. Азимутальная (1) и аксиальная (2) части
магнитной энергии, начальное аксиальное поле 2 кГс
сосредоточено между оболочками
•
•
Рис. 11. Кинетическая энергия (1) для случая без
аксиального поля. Радиальная (2) и азимутальная
3) части кинетической энергии, начальное
аксиальное поле 2 кГс сосредоточено между
оболочками
Целью 2D расчетов было ответить на следующие вопросы:
каково влияние начального аксиального поля на рост неустойчивостей;
какая часть кинетической энергии сжимающегося лайнера преобразуется в энергию сжатого
аксиального магнитного поля;
О стабилизации сжатия лайнера
383
•
наличие аксиального магнитного поля является причиной вращения лайнера. Какая часть энергии
лайнера преобразуется в кинетическую энергию вращения.
На рис. 8 и 9 приведена зависимость внутренней и магнитной энергий от времени. Влияние аксиального поля развивается только на последней стадии сжатия, когда величины азимутального и аксиального
полей становятся приблизительно равными. Энергия магнитного поля составляет 58% от внутренней
энергии, таким образом, можно сказать, что это небольшая цена за стабилизацию лайнера. На рис. 10
показана зависимость аксиальной и азимутальной частей магнитной энергии от времени. Аксиальная
часть магнитной энергии растет на финальной стадии сжатия лайнера.
Целью размещения аксиального поля между оболочками было выяснить, как аксиальное поле
смягчает удар внешней и внутренней оболочек. Отсутствие аксиального поля в оболочках уменьшает
часть кинетической энергии, переходящей в энергию сжатого аксиального магнитного поля.
Задание начального аксиального магнитного поля вызывает вращение лайнера. На рис. 11
представ-лена зависимость радиальной и аксиальной частей кинетической энергии от времени. Видно,
что для заданных параметров кинетическая энергия вращения много меньше радиальной части
кинетической энергии. Но вращение лайнера влияет на рост неустойчивостей. Эта проблема
обсуждалась выше.
Анализ массы, вовлеченной в аксиальное движение, показывает, что начальное аксиальное поле
1 или 2 кГс стабилизирует сжатие лайнера, в то время как магнитное поле 0,55 кГс приводит к росту
неустойчивостей. Поле больше 2 кГс уменьшает эффективность сжатия лайнера. Таким ообразом получили оптимальную величины для аксиального магнитного поля.
5. Заключение
Численный анализ подавления неустойчивостей для случая структурированного двойного газового
лайнера показывает, что такая нагрузка имеет более устойчивые характеристики, чем полый пинч,
однородный плазменный столб и двухкаскадный лайнер с сосредоточенными оболочками. Было
установлено, что процесс стабилизации связан с прохождением ударной волны через область с
возрастающей плотностью.
Начальное вращение лайнера приводит к появлению плотной области, расположенной на некотором
расстоянии от оси. Максимальная плотность в этой области для невозмущенного лайнера может быть
в 10 раз больше, чем максимальная плотность невращающегося лайнера. Неожиданно то, что вращение
лайнера приводит к росту неустойчивостей. При задании возмущений в невращающемся лайнере
максимальная плотность увеличивается приблизительно в 2 раза, во вращающемся лайнере плотность
увеличивается в 5 раз.
Начальное аксиальное поле 1—2 кГс стабилизирует сжатие. Потери на сжатие магнитного поля
и вращение лайнера пренебрежимо малы из-за маленького значения начального поля.
Авторы хотели бы поблагодарить Р.Б. Бакшт, А.В. Русских, А.В. Шишлова, В.И. Орешкина из HCEI за
полезное обсуждение. Работа была частично поддержана МНТЦ, проект № 525.
Список литературы
1. Gol'berg S.M, Velikovich A.L. // Phys. Fluids B. — 5 (4), 1164 (1993).
2. Tornhill J.W., Whitney K.G., Deeney C. // Phys. Plasmas. — 1994, Vol. 1. — P. 321
3. Hammer J.H., Ryutov D.D. Generation of rotation and shear flow in an imploding liner / Beams 96 proceedings. Prague, 1996. — Vol. 1. — P. 178181.
4. Diyankov O.V., Glazyrin I.V., Koshelev S.V. MAG  two−dimensional resistive MHD−code using an
arbitrary moving coordinate system // Computer Physics Communications. — 106(1997). — P. 7694.
5. Takasugi K. and Miyamoto T. Control of X−ray Spectrum Emitted from a Gas−puff Z−pinch / Proc. of the 4th
Int. Conf. on Dense Z−Pinches / AIP Conf. Proc., Dense Z−pinches. — Vol. 409. — P. 299.
6. Terry R.E., Clark R.W. Analysis of magnetic interlayer staged prs loads / AIP Conf. Proc., Dense Z−pinches. —
Vol. 409. — P. 601.
7. Sorokin S.A., Chaikovsky S.A. Proc. of the 3rd Int. Conf. on Dense Z−Pinches / AIP Conf. Proc. — 299, 83
(1993).
8. Baksht R.B., Fedunin A.V., Labetsky A.Yu. et al. Stability and K−shell Radiation of Z−pinch / AIP Conf. Proc.,
Dense Z−pinches. — Vol. 409. — P. 555559 (1997).
9. Braginskii S.L. Review of Plasma Physics / Ed. by M.A. Leontovich (Consultant Bureau, New York). — Vol. 1
(1965). — P. 205.
10. Glazyrin I.V., Karlykhanov, N.G., Kondrat'ev A.A., et al. AIP Conf. Proc., Dense Z−pinches. — Vol. 299. —
P.139144 (1994).
384
И.В. Глазырин, О.В. Диянков, Н.Г. Карлыханов и др.
11. Glazyrin I.V., Diyankov O.V., Karlykhanov N.G., Koshelev S.V. / Proc. Of the 12th Int. Conf. on High−Power
Particle Beams, Prague, Czech Republic; June 1014, 1996. — Р. 717.
12. Peterson D.L., Bowers R.L. et al., Application of 2−D Simulations to Hollow Z−Pinch Implosions / Proc. of the
4th Int. Conf. on Dens Z−Pinches, AIP Conf. Proc., Dense Z−pinches. — Vol. 409. — P. 201.
13. Russkikh A.G., Baksht R.B., Labetsky A.Yu., Shishlov A.V. Influence of preionization on dynamics of a gass
puff implosion / Proc. of the 4th Int. Conf. on Dense Z−Pinches, AIP Conf. Proc. — 409, 307 (1997).