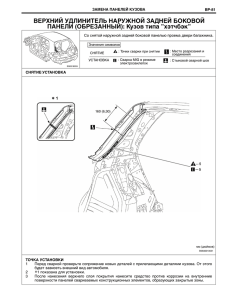
К АСИМПТОТИЧЕСКОЙ ТЕОРИИ ТЕЧЕНИЯ ВБЛИЗИ ЗАДНЕЙ

УЧЕНЫЕ
т о.м
удк
ЗАПИСКИ
УIJ!
ЦАГИ
1977
.м
J
532.526.5
К АСИМПТОТИЧЕСКОЙ ТЕОРИИ ТЕЧЕНИЯ ВБЛИЗИ
ЗАДНЕЙ КРОМКИ ТОНКОГО ПРОФИЛЯ
А. И. Рубан
Исследуется ламинарный поток несжимаемой жидкости в окрест­
ности задней кромки TOHKoro профиля при больших числах Re. Тол­
щина профиля предполагается величиной IJорядкаRе- 1 / 4 , что соот­
ветствует
режиму
с отрывом иотока
перехода
в области
безотрывного
свободного
обтекания
к
течению
взеимодеЙствия. В резуль­
тате численного интегрирования системы соотношений, описываю­
щих такие течения, найдено значение асимптотического критерия
подобия, соответствующее появлению отрыва.
Поток
в
окрестности
задней
кромки
тонкого
профиля
или
пластины является одним из наиболее известных примеров тече­
ния, которое не может быть полностью описано в рамках теории
пограничного
Блазиуса,
слоя.
так что
Вдоль
поток
пластины
эта
в пограничном
теория
слое
дает
решение
подходит
к задней
кромке с положительным трением на твердой поверхности. С дру­
гой стороны, на оси следа трение равно нулю. Исходя из этого,
в' работе
что
[1 J
в рамках теории пограничного
продолжение
решения
для
пластины
слоя
за
ее
было
показано,
заднюю
кромку
требует введения тонкого подслоя вдоль средней линии следа.
Вертикальная составляющая скорости, индуцируемая этим следом,
имеет особенность при стремлении к задней кромке. Поэтому дав­
ление во внешнем потоке в следующем приближении (по числу
Рейнольдса Re) также имеет особенность, вызывая в пограничном
слое изменения, нарастающие при приближении к задней кромке.
В результате в окрестности задней кромки появляется область
<:вобоДного взаимодействия [2, 3]. Численное решение задачи для
этой области было найдено в работе [4]. Результаты расчета пока­
зывают, что в области свободного взаимодействия трение вдоль
поверхности
пластины
остается
всюду
положительным
и
растет
при приближении к задней кромке.
Настоящая работа посвящена исследованию влИяния толщины
профиля на течение в рассматриваемой области. Толщина профиля
6
предпелагается величиней перядка Re- H .. В этом случае ЭФФеКТ
разгена петека, ебусловленный наличием задней кромки, прояв­
ляется едневременно с эффектем торможения
потока, кетерый
является следствием ненулевей телщины префиля [5]. Аналогичные
результаты
для
течения
в
екрестнести
певерхности были получены в работе
Постановка задачи. Область
точки
[6].
излома
твердей
.
свободного взаимодействия. Рас­
смотрим симметричное ебтекание тонкеге профиля двумерным
потеком несжимаемей вязкой жидкести (фиг. 1). В настоящей рабете
испельзуется ортогенальная система кеердинат СА, У), связанная с
нулевой линией те ка. Размеры етнесены. к длине префиля L, KO~1пененты скерости - к ее значению' в набегающем петоке "'00, а при­
ращение давлен ия
р
Роо
-
р-
плотность
жидкести.
c:::Jt;J-х~
. Фиг. 1
Пусть в 2
К p",~. Здесь
-
Re"":l = 'YjL",=
=
-+
О. Предпеложим, что для угла раст­
вера задней кромки имеет месте сеотношение
6 = в 1 /2 2 h.
Здесь h - некеторая полежительная пестоянная.
В этом случае в екрестности задней кромки. лежит
свобедноге
взаимодействия
[2,
З]
ебласть
О (в3/4 ). Эта область со­
длиней
стоит из трех елеев. Нижний пристенечный слой телщиной О (в 5/4 )
является вязким и еписывается уравнениями Прандтля. Для внеш­
него слоя, котерый является
потенциальным ПОТОКОм с тОлщиной
О (в 3 '4), верна ебычная линейная теерия.
По этой теерии давление
определяется через величину наклона линий тока, вызываемей
вязким педслоем. Таким образом, задачи для пристеночного слоя
и
внешнегО.
петенциальнего
потока
должны
решаться
севместно.
Средний же слой толщиной О (в) перенесится вдоль потока как
целое и не влияет в основном приближении на распределние тол­
щины
вытеснения.
Заметим, чтО. единственным отличием
течения
ности
ет
потока
в
окрестности
течки
рассматриваемего здесь
излома
твердой поверх­
является наличие следа, где условие прилипания должно
[6}
быть заменено на услевие
равенства
нулю трения
вдель нулевой
линии тека. Это езначает, что. течение в области свебедного взаимо­
действия описывается следующим образом:
и=
V
=
и ди_
dX
и
= У + .. ,
-
6314 а 314
+V
ди
дУ
при Х
-
U (Х. О)
V,
р
+ d~
-i> -
61/2
=
00
О при Х
3h
Е
_ 1п -5-:'3'-:( -4
l~
а"
д2 !!
дУ2'
dX
=
=
=
или у
< О;
в 1 !4 а 1 / 4 и
..... '
ди
д~
дХ
00,
_')
a 1i2p J
+
дV
дУ
'
=
О
,
V С Х, О) = О,
-
--= = О при Х
дУ
,
> О;
1
на действительной оси
Imj= Y~+O, р (Х)
ReJ,
=
где
0=
и
f
v
_,
Нm
У-+НО
уо={ах при Х > О
V
О
при Х<О
(z) аналитична в верхней полуплоскости,
j= ~
lпz
1t
+ 0(1)
при
Критерий подобия а определяется
z -+
00.
соотношением
cx=h/a1/2,
где а
-
безразмерная
величина трения
на
стенке
при Х
=О
для
пограничного слоя, лежащего слева от области свободного взаимо­
действия.
Численный расчет.
Численное
интегрирование
задачи для
области свободного взаимодействия проводилось с помощью ме­
тода
конечных
разностей.
причем
решение
соответствующей
стемы алгебраических уравнений находилось с помощью
си­
"двойной
релаксации": релаксации решения во внутренних точках расчетной
сетки
и
релаксации
Соотношения
краевого
(1)
+ v~=д2(j}
U d(j}
дХ
- _
дУ
дф
- __
v-
и- ау'
где
условия.
для пограничного слоя представим в виде
z=A(X)-~
1t
У
(2)
]
У2
I
дz
ах' ду=оо-l,
00=1+-=-+
...
3а 1
1t
дУ2'
~.
при
+ ...
V -+ + 00;
z(A', 0)=0 при Х<О; оо(Х, 0)=0 при Х>О.
Здесь (J) = дUjдУ - завихренность потока. Кроме того, введена
функция z = U - У; А (Х) - величина, входящая в асимптотическое
выражение для функции тока
I -
-
-
За
-
Y=tY2+A(X)Y-71ПУ+
...
-
при У-++оо.
Функция тока Ф определяется соотношениями
д~ф
дУ2
Введем
=
ш, Ф (Х, О) = О, ~ (Х, О) =
{X j ; Yk I
дУ
определяют
8
(3)
у=о
и предположим, что в узлах сетки известно
распределение завихренности {(J)~~)k
оси следа {(и!у""о )У)}
ul- .
на
i-й
распределение
I функции
итерации;
функции
{АУ)} и скорости вдоль
тогда
тока {ФУ\I.
соотношения
Новое
(3)
значение
вихря IШ~.+kl)} находится
по {АУ>} из уравнений
импульса и нераз­
рывности (релаксация во внутренних точках сетки):
ak ш~.+J_I
zk+l-
+ ЬkшУ.+kI\ + СkШ;:!~1 + d k = О,
Zk
=-'-(ш(.i+ 1 ) +ш(i+1))-1
Я
АУ
2
1.
}.k+l
Здесь коэффициенты
a k , bk ,
,
Ck
k = 2, ... ,
k=l, ... ,
•
N -
(4)
1,
N-l.
(5)
определяются через {iJ)~)k }, а
dk
является, кроме того, функцией завихреннасти.
Производная дш/дХ аппроксимируется
восторонней
разностью
в зависимости
левосторонней или пра­
от
знака
продольной
ско­
рости [7, 8]. Значения завихреннасти на рассматриваемой вертикали
считаются неизвестными, а для соседних вертикалей используются
ранее найденные значения завихреннасти.
Для решения уравнений
шения
в
(4), (5)
выберем
= R k ш<!+1)
-t- Q
} k
/. k-l'
k'
z k = S k ш(i+J)
+
D
f. я-1
k
ш<!+I)
}. k
= 2
' " .,
Тогда внешнее краевое условие системы
Теперь уравнения
позволяют
этих
же
прогоночные соотно­
виде:
получить
точек.
и используя
(4), (5),
.
дает
используемые в точках
значения
Рассматривая,
прогоночные
(2)
N
прогоночных
наконец,
соотношения
k=N -1, ... 2,
коэффициентов
уравнение
для
k = 2,
(5)
при
для
k = 1
получим,
что
при Х <О
_
( и ,I~у -О
..,(Ё+1)_
=j.l -
)(Ё+l)
J
= О,
Это и позволяет получить новое распределение завихреннасти
{ШУ.+k1 >} вдоль каждой вертикали.
Новое приближение для функции {АУ+l») находится из условия
взаимодействия с внешним потенциальным потоком:
J р' (t~ dt.
со
(Уо-А)"= - - '
1t
-00
t-
Х
Здесь использовалась описанная в работе
{6]
процедура (релак­
сация краевого условия).
Расхождение результатов такого расчета для случая
С результатами, полученными в [4], не превышает 1,5%.
а
=О
9
На фиг.
представлено
2
распределение
приращения давления
Ар ВДОЛЬ области свободного взаимодействия. Интересен случай
сх
0,5, когда эффекты разрежения и поджатия потока прибли­
=-
зительно уравновешивают друг друга. На левой части фиг. 3 (Х-< О)
изображено распределение трения на стенке при различвых значе­
ниях критерия подобиясх, а на правой ч-асти этой фигуры приве­
дена скорость на оси следа. Отметим, что отрицательные значения
трения на стенке и скорости вдоль оси следа соответствуют области
"р
v
/
/
V
/
у
i-""
,."
V
-
--If-
~
/
1'(
/"r....
J
г--
/
-
r>(
0,8
~
-2
/
\
....- ~
=-3
\;
L
L
ос
\.
~
L
;- l2.
;-
........
\
'"
\
r- ........ "....::!
1'.....
~
'"
-o?~ r:::::::
О!
2
Х
~
Фиг.
~
си (0,0)
Фиг.
Фиг.
отрыва потока.
4
2
Фиг.
3
5
Через х', у здесь обозначены декартовы
наты. Картина течения для а.=-З,О изображена на фиг.
показана
зависимость
критерия подобия сх.
сх= - 2,6.
величины
Видно,
что
трения
отрыв
на
конце
впервые
4.
коорди­
На фиг.
профиля
5
от
происходит при
Обсуждение результатов. Результаты расчета показывают, чТо
в общем случае область свободного взаимодействия не устраняет
разрыва
в
трении
на
нулевой
линии
тока,
который
возникает
на
задней кромке профиля . Это сглаживание происходит в меньшей
по размеру области (Х,--.., у,--.., Re-3/4 ), г де течение описывается пол­
ными уравнениями Навье - Стокса.
Сделаем некоторые замечания относительно используемого
численного метода. Во всех проведенных здесь и ранее в [6] рас­
четах
процедура
релаксации
краевого
щеЙся. Существенные ограничения,
ние
10
сходимости
решения
во
условия
однако,
внутренних
оказалась
сходя­
накладывает требова­
точках
сетки:
итерацион-
ный процесс становится расходящимся при
зонах отрыва. В данной работе, например,
схdдимости для сх, равного
достаточно больших
не удалось добиться
- 3,5.
Автор благодарит В. В. Сычева
за
руководство
Г. Л. Коррлева за помощь в проведении расчетов.
работой,
ЛИТЕРАТУРА
1. G о ) d s t е I n S. Concerolog some so)utions of the bouodary lауе!
equations 10 hydrodynamlcs. Proc. Cambridge Phll. Soc., УО). 26, part. 1,
1930.
'
2. S t е w а r t s о n К. Оп the f)ow пеас the trai1lng edge of а Hat
plate. Mathematika. N 16. 1969.
3. М е s s i t е r А. Р. Boundary-layer flow пеа! the trailing edge of а
flat plate. SIAM J. Арр). Math .• уоl. 18. N 1, 1970.
4. J о Ь е С. Е., В u r g g r а f О. R. ТЬе numerlcal solution of 'Ье asymptotic equatlons of trаШпg edge f10w. Proc. Roy. Soc. Londoo, А, vo). 340,
N 1620, 1974.
5. R i ) е у N., S t е w а r I s о n К. Traillng edge f1ows. J. Fluld МесЬ.,
уоl. 39, parl 1. 1969.
б. Ру 6 а н .А. И. К теории ламинарного отрыва ЖIiДКОСТИ от
. точки ИЗJlома твердой поверХ~Ости. .Ученые записки ЦАГИ. т. 7.
М 4, 1976.
7. I< 1 i о е Ь е r g J. М., S t е g е r J. L. Оп lamlnar bouodary-layer
separatlon. AIAA Paper N 74 - 94.
8. С а r t е r J. Е. Solutions for 1amioar bouodary layers with separation and reattachment. А)АА Paper N 74 - 583.
Рукопись
поступила
29/1 /976
г.