35 коэффициент, пропорциональный хроматической аберрации

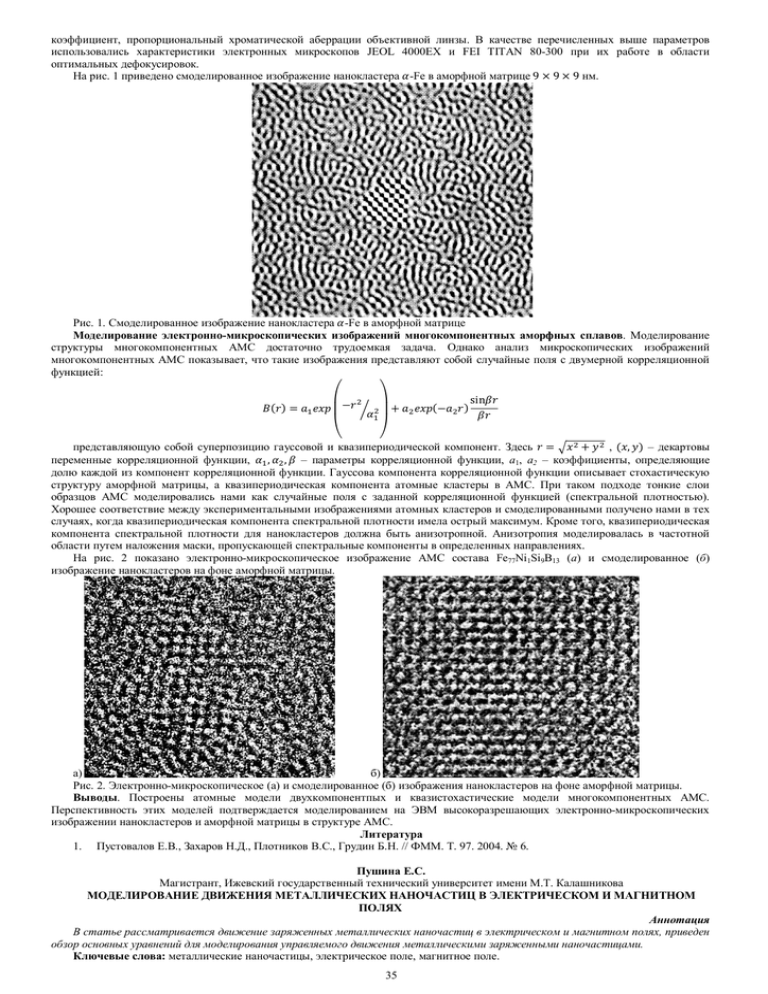
коэффициент, пропорциональный хроматической аберрации объективной линзы. В качестве перечисленных выше параметров
использовались характеристики электронных микроскопов JEOL 4000EX и FEI TITAN 80-300 при их работе в области
оптимальных дефокусировок.
На рис. 1 приведено смоделированное изображение нанокластера -Fe в аморфной матрице 9 × 9 × 9 нм.
Рис. 1. Смоделированное изображение нанокластера -Fe в аморфной матрице
Моделирование электронно-микроскопических изображений многокомпонентных аморфных сплавов. Моделирование
структуры многокомпонентных АМС достаточно трудоемкая задача. Однако анализ микроскопических изображений
многокомпонентных АМС показывает, что такие изображения представляют собой случайные поля с двумерной корреляционной
функцией:
( )=
⎛−
⎜
⎞
⎟+
(−
)
sin
⎝
⎠
представляющую собой суперпозицию гауссовой и квазипериодической компонент. Здесь =
+
, ( , ) – декартовы
переменные корреляционной функции,
, , – параметры корреляционной функции, a1, a2 – коэффициенты, определяющие
долю каждой из компонент корреляционной функции. Гауссова компонента корреляционной функции описывает стохастическую
структуру аморфной матрицы, а квазипериодическая компонента атомные кластеры в АМС. При таком подходе тонкие слои
образцов АМС моделировались нами как случайные поля с заданной корреляционной функцией (спектральной плотностью).
Хорошее соответствие между экспериментальными изображениями атомных кластеров и смоделированными получено нами в тех
случаях, когда квазипериодическая компонента спектральной плотности имела острый максимум. Кроме того, квазипериодическая
компонента спектральной плотности для нанокластеров должна быть анизотропной. Анизотропия моделировалась в частотной
области путем наложения маски, пропускающей спектральные компоненты в определенных направлениях.
На рис. 2 показано электронно-микроскопическое изображение АМС состава Fe77Ni1Si9B13 (а) и смоделированное (б)
изображение нанокластеров на фоне аморфной матрицы.
а)
б)
Рис. 2. Электронно-микроскопическое (а) и смоделированное (б) изображения нанокластеров на фоне аморфной матрицы.
Выводы. Построены атомные модели двухкомпонентпых и квазистохастические модели многокомпонентных АМС.
Перспективность этих моделей подтверждается моделированием на ЭВМ высокоразрешающих электронно-микроскопических
изображении нанокластеров и аморфной матрицы в структуре АМС.
Литература
1. Пустовалов Е.В., Захаров Н.Д., Плотников B.C., Грудин Б.Н. // ФММ. Т. 97. 2004. № 6.
Пушина Е.С.
Магистрант, Ижевский государственный технический университет имени М.Т. Калашникова
МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ МЕТАЛЛИЧЕСКИХ НАНОЧАСТИЦ В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ
ПОЛЯХ
Аннотация
В статье рассматривается движение заряженных металлических наночастиц в электрическом и магнитном полях, приведен
обзор основных уравнений для моделирования управляемого движения металлическими заряженными наночастицами.
Ключевые слова: металлические наночастицы, электрическое поле, магнитное поле.
35
Pushina. E.S.
Master student, Izhevsk State Technical University named after MT Kalashnikov
MOTION SIMULATION OF METALLIC NANOPARTICLES IN ELECTRIC AND MAGNETIC FIELDS
Abstract
The article considers the motion of charged metal nanoparticles in electric and magnetic fields, provides an overview of the basic
equations for modeling controlled motion charged metal nanoparticles.
Keywords: metal nanoparticles, electric field, magnetic field.
Электрические и магнитные поля, как правило, действуют на движущиеся заряженные металлические наночастицы с
известной силой, поэтому эти поля могут использоваться для управления движением заряженных металлических наночастиц.
Описание движения заряженной металлической наночастицы проводится на основании второго закона Ньютона:
(1)
⃗ = ⃗ + ⃗ × ⃗,
⃗
где
− сила, действующая на металлическую наночастицу с электрическим зарядом со стороны электрического поля;
⃗ × ⃗ − сила Лоренца, действующая на металлическую наночастицу со стороны магнитного поля. В общем случае напряженность
электрического поля ⃗ и индукция магнитного поля ⃗ могут зависеть от координат и времени [1]. Для однозначного решения
уравнения (1) его необходимо дополнить начальными условиями: положением наночастицы и скоростью в некоторый момент
времени .
При описании распространения потоков металличсеких наночастиц в некоторых случаях необходимо также учитывать
взаимодействия наночастиц между собой, или принимать во внимание зависимость характеристик полей от положения и скоростей
других наночастиц. Наконец, при записи уравнения (1) принято, что наночастицы движутся в вакууме, где отсутствуют силы
сопротивления среды. При движении наночастиц в электромагнитном поле, как правило, пренебрегают действием силы тяжести,
которая обычно значительно меньше электромагнитных сил.
Записанное уравнение движения справедливо для заряженных металлических наночастиц и для частиц, движущихся со
скоростями, значительно меньшими скорости света.
Заряженная наночастица в электростатическом поле
Рассмотрим так же процессы движения металлических наночастиц в электростатическом поле. Уравнение движения частицы в
электростатическом поле имеет вид:
(2)
⃗ = ⃗( , , ),
Так как электростатическое поле является потенциальным, то для движущейся наночастицы выполняется закон сохранения
энергии, на основании которого можно записать уравнение:
(3)
+ ( , , )=
,
2
где ( , , ) − потенциал электростатического поля.
Работа сил поля не зависит от формы траектории наночастицы (Рис.1.) и равна произведению заряда металлической
наночастицы на разность потенциалов между начальной и конечной точкой траектории:
(4)
−
= ( − ),
2
2
Обращая внимание на расстановку индексов в уравнении (4), следует, что увеличение кинетической энергии наночастицы
равно уменьшению ее потенциальной энергии.
Рис.1 – Изменение траектории движения наночастицы из положения 1 в положение 2 в электростатическом поле.
Движение заряженной частицы в однородном электрическом поле.
В однородном электрическом поле, сила, действующая на заряженную наночастицу, постоянна как по величине, так и по
направлению. Поэтому движение такой наночастицы полностью аналогично движению тела в поле тяжести земли без учета
сопротивления воздуха. Траектория наночастицы в этом случае является плоской и лежит в плоскости, содержащей векторы
начальной скорости наночастицы и напряженности электрического поля (Рис.2.). Поэтому для описания положения наночастицы
достаточно двух координат. Удобно одну из декартовых осей координат рассматривать вдоль направления вектора напряженности
поля (тогда движение вдоль этой оси будет равноускоренным), а второй перпендикулярно вектору напряженности (движение вдоль
этой оси − равномерное). Начало отсчета удобно совместить с начальным положением наночастицы. Простейший примером
является наночастица массы , несущая электрический заряд движется в однородном электрическом поле напряженности , в
начальный момент ее скорость равна . Выберем ось
в сторону противоположную направлению вектора , начало отсчета
совместим с начальным положением частицы.
Рис. 2 – Движение металлической наночастицы в однородном электрическом поле
Наночастица будет двигаться с постоянным ускорением направленным вертикально вниз, поэтому дальнейшее описание
движения, со всеми его особенностями можно рассматривать как задачу о движении тела в поле тяжести без учета сопротивления
воздуха:
36
(5)
⃗=
Плоское движение заряженной частицы в однородном магнитном поле.
При движении заряженной металлической наночастицы в магнитном поле на нее действует сила Лоренца, которая, как
известно, направлена перпендикулярно вектору скорости наночастицы, поэтому эта сила работы не совершает. Следовательно, при
движении наночастицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются −
изменяется только направление вектора скорости частицы.
Рассмотрим движение заряженной металлической наночастицы в однородном магнитном поле, когда вектор скорости
наночастицы направлен перпендикулярно вектору индукции магнитного поля (Рис.3.). Так как модуль скорости наночастицы
сохраняется, сила Лоренца перпендикулярна вектору индукции поля , то вектор скорости все время будет перпендикулярен
вектору индукции поля.
Рис. 3– Движение заряженной наночастицы в однородном магнитном поле.
Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца
также будет оставаться постоянным и равным:
(6)
=
,
Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так как ее модуль постоянен, то и
кривизна траектории наночастицы будет постоянна, то есть траекторией наночастицы будет окружность. Радиус этой окружности
можно найти на основании уравнения второго закона Ньютона:
(7)
=
,
из которого находим радиус окружности:
=
(8)
,
Найдем период обращения частицы в магнитном поле:
2
=
=2
(9)
,
Из формулы (9) следует вывод − период вращения наночастицы в магнитном поле не зависит от ее скорости. Частота вращения
выражается формулой (10) и называется циклотронной частотой:
1
1
(10)
= =
,
2
Рассмотренные виды управления движением металлических наночастиц составляют далеко не полный список [2], в настоящее
время ведется работа по написанию программного комплекса для визуализации данных видов движения металлических
наночастиц.
Литература
1. Электронный учебник физики для профильника [Электронный ресурс] URL: http://fizportal.ru/physics-book-50 (дата
обращения 21.02.2014).
2. Jorgensen W.I., Tirado-Rives J.J. Comput. Chem. 2005. V. 26. No. 16. P. 1689-1700.
Савельева Е.А.¹, Щербачева А.О.²
¹Магистрант, Ижевский государственный технический университет им. М.Т. Калашникова; ²Магистрант, Ижевский
государственный технический университет им. М.Т. Калашникова
ИССЛЕДОВАНИЕ ДВУХФАЗНОГО ТЕЧЕНИЯ ВЯЗКОЙ НЕЖИМАЕМОЙ ЖИДКОСТИ В ПЛОСКОМ
ПРЯМОЛИНЕЙНОМ КАНАЛЕ
Аннотация
В статье рассмотрено исследование течения вязкой несжимаемой жидкости с частицами. Течение двухфазной жидкости
описывается дискретно траекторным методом Эйлера-Лагранжа, где для описания жидкой фазы используется система
уравнений Навье-Стокса, а для описания движения частиц – уравнение Лагранжа. Рассчитана траектория движения частиц в
потоке.
Ключевые слова: Двухфазное течение, несжимаемая жидкость, плоский канал, метод подобия.
Saveleva E.A.¹, Sherbacheva A.O.²
¹Magistrant, Izhevsk state technical University. M.T. Kalashnikov; ²magistrant, Izhevsk state technical University. M.T. Kalashnikov
INVESTIGATION OF TWO-PHASE FLOW OF VISCOUS NAJIMAEM FLUID IN A FLAT STRAIGHT CHANNEL
37