нахождение ожидаемых доходов систем замкнутой структуры

О- М. КИТУРКО, М. А. МАТАЛЫЦКИЙ
НАХОЖДЕНИЕ О Ж И Д А Е М Ы Х ДОХОДОВ СИСТЕМ ЗАМКНУТОЙ
СТРУКТУРЫ МАССОВОГО О Б С Л У Ж И В А Н И Я
В работе проведен асимптотический анализ ожидаемых доходов отдельных систем
злмхнутой структуры массового обслуживания с однотипными заявками.
Выведено
обыкновенное дифференциальное уравнение для нахождения ожидаемого дохода при определенных начальных условиях. Рассмотрен пример, когда изменение параметров носит
сезонный характер.
Введение
Рассмотрим замкнутую сеть массового обслуживания (МО), состоящую из те-f 1 систем массового обслуживания (СМО) 5о, Si, ..., Sn, общее число однотипных заявок в которой в момент
времени t составляет К{f). Обычно под системой So понимается внешняя среда, а под системами S|, S-2, • • •, 5',, - конкретные СМО сети, в которых производится обслуживание заявок. Сети
МО, являющиеся замкнутыми по структуре, но в которых общее число обслуживаемых заявок не
постоянно, а зависит от времени, впервые исследованы в частных случаях в [1| и названы замкнутыми структурами обслуживания (ЗСО). Пусть пц(Ь) - число линий обслуживания в системе Si,
г = 1, п, положим, mo(t) = K(t) и времена обслуживания заявок каждой из линий распределены
по показательному закону с интенсивностью m(t), т а к ж е зависящей от времени. i,j = 0, п. З а я в к и
па обслуживание выбираются в соответствии с дисциплиной FIFO. З а я в к а , обслуживание которой в системе St закончилось, с вероятностью pij(t) переходит в систему 5-у,
= 0 , п . Матрица
вероятностей переходов P(t) = ||pij(£)||> hj — 0 , п , является в к а ж д ы й момент времени матрицей
=
вероятностей переходов неприводимой марковской цепи, 0 < pij(t) < 1.
1- Основная
задача исследования заданной ЗСО состоит в асимптотическом анализе марковского процесса,
описывающего её поведение при большом числе заявок.
Состояние структуры в момент времени I описывается вектором
k(t) = (М) = (ki,k'2,...,kn,t)
=
(h(t),b2(t),...,kn(t)),
где kt(t) число заявок в системе 5, в момент времени t, t € [0,Т], г = 0, п, который образует 77мсрный марковский процесс с непрерывным временем и конечным числом состояний. Очевидно,
что число заявок в системе 5q равно ko(t) — K(t) — Yli= i &»(£)•
Нахождение ожидаемого дохода отдельных систем
Нахождение общего ожидаемого дохода замкнутой структуры массового обслуживания с
однотипными заявками было рассмотрена в [2]. Поставим теперь задачу прогнозирования ожидаемого дохода отдельной СМО 5 С , с = 1 ,п. Обозначим через Vc(k, t) полный ожидаемый доход,
киторый получит С М О Sc за время t, если в начальный момент времени она находится в состоянии (k,t). К а к указано ранее, в течение малого промежутка времени At З С О может остаться в
с остоянии (k. t, + At) либо совершить переход в состояние (к + /г — t + At), i,j = 0,п.
Теорема. Плотность распределения дохода
t) при условии, что она дифференцируема
ио t и д в а ж д ы кусочно-непрерывно дифференцируема по хг, г = 1 .п. удовлетворяет с точностью
до членов порядка малости e 2 ( t ) = щ у дифференциальному уравнению в частных производных:
291
t=l
ij=l
- n х д е р Ы * . 0 + r e(*) + K{t) Y , bj{t)Vji{t) m i n & ( « ) , t j W t ) , с = 1, n.
ij=0
(1)
,Г *азсп«льство. Будем считать, что если на интервале времени [t.t + At] ЗСО сом-ршает переход из состояния (к. t) в состояние (к + /, — Ij.t + At) с вероятностью
*
" ' kj(t))At+o(At).
то доход системы Sr составит RJlc{t) плюс ожидаемый доход
• -г — I t который она получает за оставшееся время t, если бы начальным было состояние
• -г /< - /,.t . Кроме этого, будем считать, что система Sc получает доход в размере Rc(t) з а
лнннцу времени в течение пребывания З С О в состоянии (k,t). З С О остаётся в состоянии (к. t)
. к юние малого промежутка времени At с вероятностью 1 - ] Г " = 0 / ^ t ) т ш ( т г ( ? . ) ,
при
этом доход СМ О S, составит Rr(t)At + Vc(k, t).
Тогда полный ожидаемый доход Vc[k,t + At) в момент времени (t + At) удовлетворяет следующей системе разностных уравнений:
Vc(k,t + At) = j l -
^ / i J ( t ) m i n ( m 7 ( t ) ! f c j ( t ) ) j Atj
{Rc(t)At +
Vc(k,t))+
«
+ ^ Hj{t)pji(t) miri(m,-(t), kj(t))M (Rjic(t) + Vc{k + U - Ij,t)) + o(At),
i,j-0
которая сводится к системе РДУ;
m i n ( m ^ i ) , М О ) (Vc(k + h - Ij, t) - Vc(k, t)) +
= Е
j,i=o
n
+ E t*jit)Pji(t)
i,j=0
mill{rn j (t),k j {t))R j i c (t) + R,:{t), с = TJi.
(2)
Далее, как и ранее, перейдём к плотности распределения дохода СМО Sc, которую обозначим
vc(x,t). При K(t) -4 ос:
Vc{k, t) = Vc(xK, t) = en{t)vс(хЛ)
Кроме того, при K(t)
ским равенствам
или vc(x,t) = Kn(t)Vc(xK,
t).
(3)
oo доходы RjiC(t) и Rc(t) удовлетворяют следующим асимптотиче-
Kn(t)Rjic(t)
= rjic(t),
I<n(t)Rc(t)
= r c (t).
(4)
Уравнение (2) д л я плотности распределения дохода с учетом (3), (4) может быть представлено в виде
=
+K{t)
~nK(t)e'{i)vc{x,t)+
У ] lh(t)Pj,(t) m i l l e t ) , Z j ) (t? c (i + el-eJ,t)
-K(t)
Y , Mj-(t)Pji(0
i.j=о
- vc(x, t)) +
Xj)rjic(t)
(5)
+rc(t).
.. златая, что t c ( i , t ) дифференцируема rio t и дважды кусочно-непрерывно дифференцируем* по xiz i = 1.П, можно разложить функцию » ( x + « j в ряд Тейлора в окрестности точки
{Е. • используя члены до второго порядка включительно:
г
'с{х + е, - е„ t) = гф,
e2(t) (д\ф,
t)
+ —2 I
57.2
дх
t) + e(t) (
-
Эх,
, +
дх.
9 Ч М
d2vc(x,t)\
.
2
е
2
2 -dxjdxj
U 1 T +
а_2
I
+
°
(
(
0
)
,
дх -
.
•?>
=
Поэтому уравнение (4) можно записать в виде
Ot
2
i J-0
у
PiWPjitt)
дх]
dvc(x, t)
<9.T;
mm{l}(t),'xj)
(9a-,
+
nAT(t)e'(*K0M)+
+
" dxidxj
dvc(x, t)
X ] ^(t)Pii(t) min^Ct),
t,j=0
+
c = l,n.
Последнее уравнение с точностью до членов порядка 0(е 2 (£)) можем записать в более компактном
виде (1). Теорема доказана.
Используя рассуждения, как в предыдущем пункте, приходим к следующему дифференциальному уравнению д л я среднего по х значения дохода системы Sc при условии изменения
начального состояния (ж, t) в области G:
dt
WTc(t)
NK
h—foT.
Li=l
^ E E ^ T ^ F ^ W
^ > j = i i=0
W £ № VG~c(t) +
II -
mm(lj(i),xj)dx+
с
/ / • • • / F I - Ё Ч ) / * ,
i-O
G
\
j=l
)
(6)
G
Зададим, как и ранее, разбиение: fio(l) = {1, 2, .... n}. fti(l) = { 0 } , т = 1, что соответствует
наличию очередей в С М О Si. Si, .... Su. Тогда, решая уравнение (6) при начальном условии
= Sc-. можно определить средний ожидаемый доход при изменении начального состояния
по области G1 = {x{t) : li(t) < ц < 1,* = 1,п,
хг < l } . Уравнение (6) при этом имеет вид
203
to(t)£poi(t)-nK(t)e'(t)
at
n ( G ,-)
У
tij(t)Mt)Tni(t)rMt)+
Y
—л.': ^ м М я к Ю п ы с С ) / /
1
/
J
n.
( 1 - Ё X j,
V
J-l
+ rc{t), С = 1,1
dx
(7)
Пример
Пусть транспортное предприятие (ТП, система S n ) посылает автомобили (заявки), д л я выполнения перевозок между различными городами (внешняя среда, система So). После этого они
возвращаются на базу ТП. предварительно пройдя в ряде пунктов (системы S i , S2,
S«-i)
технический осмотр, который может т а к ж е включать и ремонт автомобилей. Количество функционирующих линий обслуживания в пунктах Si, S2, ..., Sn-i в момент времени t равны соответственно m\(t). m-2(t), . . . , m n _ j ( t ) . В системе Sn осуществляется погрузка автомобилей перед
выходом в рейс, которой занимаются rrin(t) бригад погрузки
Аналогичная ситуация может возникнуть когда автомобили возвращаются из внешней среды
и разгружаются па складах Т П (системы S i , S 2 , . . . , S „ _ i ) ; в этом случае rri\{t), rn2(t).....
mn-\{t)
количество бригад разгрузки соответственно на складах S i , S2, . . . , Sn-1 •
В данном случае моделью функционирования перевозок является З С О . изображенная па
рисунке 1. Матрица P(t) при этом имеет вид
/
0
0
0
Р01 ( 0
0
0
Pm{t)
0
0
• •
Po,n-\(t)
0
0
0
1
1
\
,
P ( 0 = IIPi 3 WII ( , 1 + i ) x ( n + i) =
0
V 1
II— 1
0
0
0
0
0.
0
Рисунок 1 —Модель передвижения
1
1 /
=
j=1
автомобилей
V i e [Го,г].
-
- -
параметров З С О носит сезонный характер, например, интервал [То, Г] разбит
промежутков. Положим, что
-л*.
Kit)
' /4 1 } , t e [ T 0 , r i ) ,
' К\, t € [Го,ГО,
А' 2 , * € [ Г Ь Г 2 ) ,
=
j = 0 , n,
г е [Г,_ьГ]
l
I
<€[Г,_ЬГ],
m j l \ t б [Г0.Г1),
:
Я»д о =
tetro.ro
. t € [ГьГа).
•
„(2)
р%>,
т—
m ^ t e l V b T ] ,
рМ
t € Р1.Г2),
•
1
т
t e l T ^ T j ,
Найдем с е д и н е доходы системы 5 С
г = l.q. Пусть т а к ж е доходы от переходов м е ж д у
состояниями З С О также являются кусочно-постоянными ф у н к ц и я м и с несколькими интервалами
постоянства:
(
Ji)
'
r , j c ( t ) = ^ r fif*i , t e [ Г Ь Г 2 ) ,
I rjt
l Г ^ , t e [т,,_ьГ].
te[r„_bT],
П-1
на интервале [To.Ti). Уравнение (7) в этом
71— 1
-
Mo vu(t) +
Г
.
/ . Mj "l j ' jnc
j=l
m(G 1
n
Г (
\
H - 5 > dx +
JJ
Y
>/
G, • V
•
то есть
dvli(t)
——
'
[го.г,)
t e [Гх,г2),
j = 0. n. r(t) = <
Найдем вначале ожидаемый доход С М О 5 С v\c(t)
случае имеет вид:
dvTcjt)
dt
t e
f
)
Mn 'U7l ' n(
nOc
= Mo^V!c(t) + Г 1 с , t'i c (To) = ''.'o!:!
(i)
(1)
Ц0 Vic(t) = Пе, i'l,(T 0 ) = V ^ .
Его решением является
*й(*> = U c
\
]
+
^
Mo /
, ( t
-
T ( l )
[ T o ,
Г).
Mo
Найдем теперь ожидаемый доход СМО Sc v-2e(t) па интервале [ТьГг). Уравнение (7) па этом
интервате принимает вид
295
dv*(t)
dt
Mo2)y2c(0 + rc,
n-l
m (GO
71— 1
£ "F'
>•£+TF
j-I
Ci
\
+
£
/
в качестве начального условия нужно взять г ъ ( 2 \ ) = ^ ( Г ) . Решением уравнения (8) является
- ИГ + ~т I - -щ-> < Е Т , Г 3 ) .
/20 1
На интервале [Г 2 ,Г 3 ) будем иметь
V
Мо
Мо /
,iV
Мо
tf)
(2)
J'O
„(3) ,
/х0
С
. (3)'
Мо
I 2' з) 1
где
n-l
=
m(G,)
E
n-l
^ m f r f i+
E
+
«
X
I rb; + rf>
;=i
G,
Ha i-ом интервале [ Г _ ь Г ) имеем:
d ^ ( Q _ (i)
= iA'wS)
dt
+ r iC)
= ®г=т7№_1),
где
n-l
Tic =
m(Gi)
n-l
E
j=l
+
.(
+
n
\
i-Tr.Adx
E
.7=1
+ '.f'
' GX " V
Решением уравнения (9) является
-
( —c(Ti-г)
+ ^
I
4
Ao /
На последнем г/-ом интервале [Г 9 _1,Г]:
_ i (0
| (:
Mo
t €
[Гг_ьТ(),
(9)
•-1
V
—
^
J I
Pj
m
j
r
j n c + А1» " 4 .
х
nOc •
I ^ + Г"Ч)
1- Е
Тогда
V
/С /
мо
Пусть а — 5, а интервал [То, Т] разбит на q = 4 различных промежутка. Предположим, что
У(0) = 0. Параметры ЗСО. кроме доходов от переходов между состояниями сети, пусть остаются
томи же. Найдём средний доход центральной СМО S 5 . Предположим, что доходы от переходов
между состояниями ЗСО также являются кусочно-постоянными функциями с q = 4 интервалами
постоянства:
' 1.8,
2.5.
] 1-6,
I 2.7,
t
t
t
i
е
€
€
€
[о,
[1.
[2.
[3,
1),
2),
3),
4],
0
0
0
0
0
0
0
0
0
0
8
.
5
0
V
0
0
0
0
0
0
0
0
0
0
0
0
0 0
0 3.4
0 4
0 9.5
0 1.3
0 0
\
/
0
0
0
0
0
0
0
0
0
0
-3.6 0
0
0
0
0
0
0
0
0
I)
0
0
0
0 0
0 3.5
0 4.8
0 8.9
0 5.6
0 0
\
0
0
0
0
0
0
^ ( 0 = 1^1 =
0
0
0
0
\ -8.2 0
0
0
0
0
0
0
0
0
0
0
0
0
0 0 \
0 5.4
0 8.9
, t € [ 2 , 3),
0 9.6
0 1.6
0 0 /
/
r (i)
ijO
/?f(t) =
V
f
,
t
€ [0, 1)
, t € [1, 2)
297
0
0
0
0
0
8
.4
V
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0 0
0 8.3
0 4.3
0 5.4
0 9.9
0 0
\
/
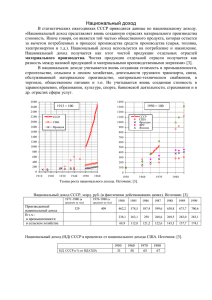
И э м а п в г ( щ д а а ю г о дохода системы на интервале представлен па рисунке 2.
:
з
4
Р и с у н о к 2 — О ж и д а е м ы й д о х о д с и с т е м ы So
Список
литературы
1. Китурко, О.М. Асимптотический анализ общего ожидаемого дохода замкнутой структуры массового обслуживания с однотипными заявками и со применение /О. М. Китурко, М. А. Маталыцкий,
Т. В. Русилко// Всегник ГрГУ. Сер.2. 2013. 1.
2. Маталыцкий, М.А. Математический анализ стохастических моделей обработки исков в страховых
компаниях. Монография./М.А. Маталыцкий. Т.В. Русилко
Гродно: ГрГУ. 2007. 334 с.
Китурко Ольга Михайловна, аспирант кафедры стохастического анализа и экопометрического моделирования факультета математики и информатики Гродненского государственного университета им.Янки
К у налы, sy t ay a_om@mail.ru.
Маталыцкий Михаил Алексеевич, заведующий кафедрой стохастического анализа и эконометриноского моделирования факультета математики и информатики Гродненского государственного университета им.Янки Купалы, доктор физико-математических наук, профессор, m.matalytski@ginail.com.