Планирование закупок и сбыта дефицитных товаров в среде
реклама
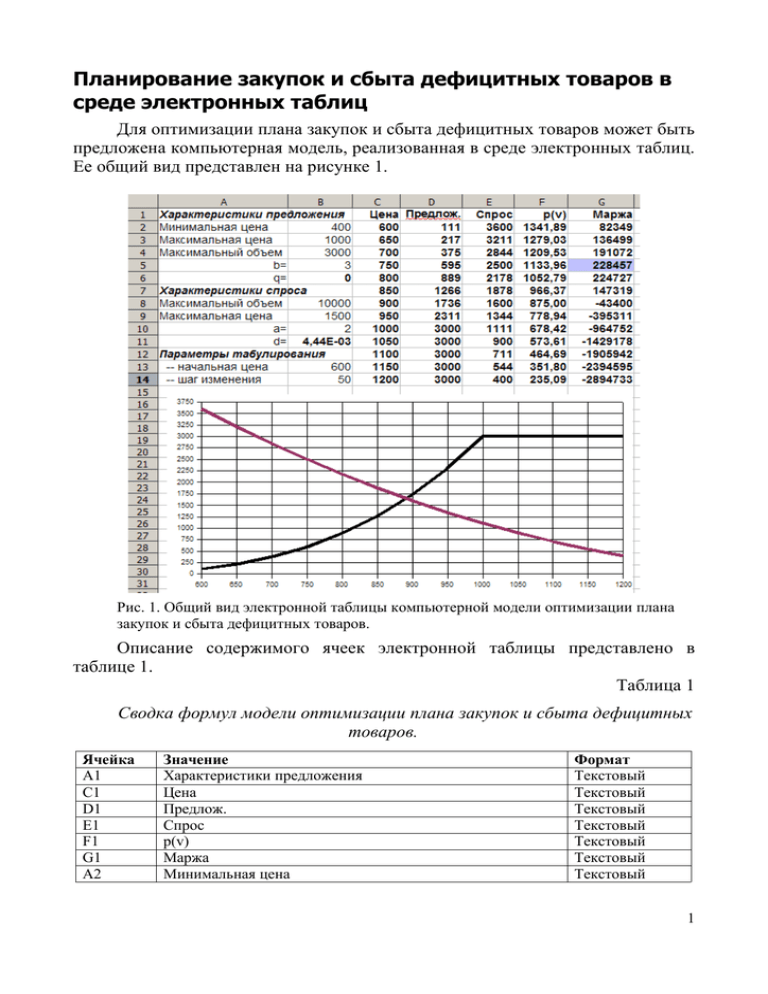
Планирование закупок и сбыта дефицитных товаров в среде электронных таблиц Для оптимизации плана закупок и сбыта дефицитных товаров может быть предложена компьютерная модель, реализованная в среде электронных таблиц. Ее общий вид представлен на рисунке 1. Рис. 1. Общий вид электронной таблицы компьютерной модели оптимизации плана закупок и сбыта дефицитных товаров. Описание содержимого ячеек электронной таблицы представлено в таблице 1. Таблица 1 Сводка формул модели оптимизации плана закупок и сбыта дефицитных товаров. Ячейка A1 C1 D1 E1 F1 G1 A2 Значение Характеристики предложения Цена Предлож. Спрос p(v) Маржа Минимальная цена Формат Текстовый Текстовый Текстовый Текстовый Текстовый Текстовый Текстовый 1 Ячейка B2 A3 B3 A4 B4 A5 B5 A6 B6 A7 A8 B8 A9 B9 A10 B10 A11 B11 A12 A13 B13 A14 B14 C2 C3 D2 E2 F2 G2 Значение <Ручной ввод> Максимальная цена <Ручной ввод> Максимальный объем <Ручной ввод> b= <Ручной ввод> q= =B4/(B3-B2)^B5 Характеристики спроса Максимальный объем <Ручной ввод> Максимальная цена <Ручной ввод> a= <Ручной ввод> d= =B8*B9^(-B10) Параметры табулирования -- начальная цена <Ручной ввод> -- шаг изменения <Ручной ввод> =B13 =C2+$B$14 =ROUND(IF(C2<$B$2;0;IF(C2>$B$3;$B$4;$B$6* (C2-$B$2)^$B$5))) =ROUND(IF(C2>$B$9;0;$B$11*($B$9-C2)^$B$10)) =$B$9-(($B$6/$B$11)^(1/$B$10))* (C2-$B$2)^($B$5/$B$10) =ROUND(F2*D2-C2*D2) Формат Числовой Текстовый Числовой Текстовый Числовой Текстовый Числовой Текстовый Числовой Текстовый Текстовый Числовой Текстовый Числовой Текстовый Числовой Текстовый Числовой Текстовый Текстовый Числовой Текстовый Числовой Числовой Числовой Числовой Числовой Числовой Числовой В диапазоне ячеек A1:B6 содержатся данные, характеризующие функцию предложения дефицитного товара. В ячейке B2 вручную задается экспертная оценка минимальной цены товара, ниже которой его продажа поставщиком невозможна. В терминах рассмотренной в предыдущем параграфе модели – это значение параметра v min . В ячейку B3 вручную вводится значение максимальной цены, по которой может быть скуплен весь доступный объем дефицитного товара ( v max ). В ячейку B4 вводится оценка максимального объема доступного дефицитного товара ( Q max ), который может быть скуплен при цене большей или равной v max . В ячейку B5 вручную вводится оценка параметра b функции предложения дефицитного товара. На основе этих данных в ячейке B6 рассчитывается параметр q функции предложения дефицитного товара. Для этого используется формула =B4/(B3B2)^B5. В диапазоне ячеек A7:B11 содержатся данные, характеризующие функцию спроса на дефицитный товар со стороны покупателей посредника. В 2 ячейке B8 вручную задается оценка параметра объема максимального спроса на товар ( D max ). В ячейку B9 вручную вводится максимальная цена, начиная с которой по предположению посредника товар не будет востребован ( pmax ). В ячейку B10 вводится параметр a функции спроса на товар. На основе этих данных, в соответствии с формулой (3.1.16) рассчитывается величина параметра d функции спроса. В диапазоне ячеек A12:B14 задаются параметры табулирования функций спроса и предложения. В ячейку B13 вручную вводится начальная цена, а в ячейку B14 – шаг ее изменения. В ячейках C2:C14 формируются цены, используемые для табулирования функций спроса и предложения, значения которых отображаются в числовом и графическом виде. Для этого в ячейку C2 копируется значение начальной цены, введенное в ячейку B13. В последующих ячейках данного столбца вычисляются новые цены путем прибавления к предыдущей значения шага изменения, заданного в ячейке B14. Здесь формулы однотипны, поэтому в таблице 1 представлена только формула для ячейки С3: =C2+$B$14 В соответствии с ней к значению цены в ячейке C2 прибавляется величина шага изменения цены, заданного в ячейке B14. Все остальные формулы расчета цены в ячейках C4:C14 могут быть получены копированием формулы из ячейки С3 стандартными средствами электронных таблиц. В диапазоне ячеек D2:D14 рассчитываются значения функции предложения, соответствующие ценам из диапазона C2:C14. В таблице 1 задано определение расчетной формулы только для ячейки D2, поскольку во все остальные ячейки данная формула может быть скопирована стандартными средствами электронных таблиц. В диапазоне ячеек E2:E14 рассчитываются значения функции спроса, для цен из диапазона C2:C14. В ячейках F2:F14 формируются значения цен продажи, уравновешивающих объем предложения, вычисленный в той же строке таблицы со спросом. Это значения цены p v , расчитанные для значения цены предложения v из той же строки таблицы. Например, в ячейке C2 содержится цена, для которой в ячейке D2 рассчитывается объем предложения дефицитного товара поставщиком. Для этого объема предложения в ячейке F2 рассчитывается цена, по которой этот объем товаров может быть распродан в соответствии с функцией спроса. То есть в ячейке C2 приведено значение цены предложения v, в ячейке D2 – соответствующий ей объем предложения дефицитного товара поставщиком (значение Q v ), а в ячейке F2 – цена p v , уравновешивающая данный объем предложения со спросом. На основе цены равновесия данного объема предложения и спроса, в ячейках G2:G14 рассчитывается соответствующая данным параметрам маржинальная прибыль посредника. Порядок использования компьютерной модели состоит в следующем. 3 Сначала использующий ее экономист, полагаясь на экспертные оценки должен построить функции предложения и спроса на исследуемый товар. Для построения функции спроса задаются экспертные оценки: а) минимальной цены ( v min ) – цены поставки, ниже которой переговоры с поставщиком бессмысленны, поскольку ниже этой граничной цены он не будет поставлять дефицитный товар; б) максимальной цены ( v max ) – минимального уровня цены, при которой по предположению посредника может быть скуплен весь запас товара поставщика. Это также может быть цена, при которой поставщик гарантированно поставит необходимый посреднику объем искомого товара; в) максимального объема товара ( Q max ), имеющегося у поставщика, который при соответствующей договоренности может быть полностью получен посредником при цене не меньшей, чем v max . При построении функции предложения задается также параметр b, характеризующий степень заинтересованности поставщика в поставках своего дефицитного в зависимости от роста цены предложения. Порядок задания этого параметра трудно формализовать и здесь эксперт должен, в основном, полагаться на свое чутье и имеющиеся у него предположения о возможном поведении поставщика. Расмотрим различные варианты поведения кривой предложения при разных значениях параметра b. При b=1 предложение товара (возрастающая прямая) нарастает строго пропорционально увеличению цены (см. рисунок 2). Рис. 2. Линейная функция предложения дефицитного товара. При b=5 предложение товара медленно нарастает при относительно малом увеличении цены по сравнению с минимальным порогом, но потом начинает расти очень быстро (см. рисунок 3). 4 Рис. 3. Медленное увеличение предложения при малых изменениях цены по сравнению с минимальной и быстрое нарастание при значительном увеличении цены закупки. Такое поведение кривой предложения характерно для случая, когда у поставщика много предложений на закупку по ценам из среднего диапазона и когда цена нового предложения находится в нем или близко к нему, он слабо реагирует на такое предложение. Однако, когда предлагаемая ему цена закупки переходит за предел большинства предложений на закупку по средним ценам, он начинает охотнее вести переговоры о возможности поставок при высокой предложенной цене закупки. На приведенном рисунке видно, что при предлагаемой цене закупки в 850 он готов поставить только 750 условных единиц товара, при цене 950 – уже 2000 условных единиц, а при цене 1000 – готов расстаться со всем имеющимся у него дефицитным товаром. При значениях 0b1 кривая предложения быстро нарастает уже при малых изменениях предлагаемой цены закупки по сравнению с минимальной, но потом рост относительно стабилизируется (см. рисунок 4). Такое поведение поставщика характерно в том случае, когда у него много предложений на закупку по минимальной цене и нет предложений на закупку по достаточно высоким ценам. В этом случае, даже при небольшом повышении цены относительно среднего уровня предложений он охотно готов вести переговоры о достаточно больших поставках по такой цене, но при этом все-таки не готов расстаться со всем товаром, ожидая поступления заявок на поставки по еще более высоким ценам. 5 Рис. 4. Быстрое увеличение предложения при малых изменениях цены по сравнению с минимальной с последующей стабилизацией роста при высоких ценах. Задавая различные комбинации параметров v min ,v max ,Q max , b следует стремиться к тому, чтобы подобрать как можно более реалистичную кривую предложения дефицитного товара его поставщиком. Для этого нужно внимательно изучать расчетные данные предложения по разным ценам и давать экспертное заключение об их соответствии действительности. Здесь все зависит от интуиции экономиста и его знания рынка, на котором он работает. Сказанное относится и к проблеме формирования кривой спроса на товар. Для ее формирования задаются оценки: а) максимального объема спроса ( D max ) – потребности в данном товаре без учета ограничений платежеспособного спроса; б) максимальной цены ( pmax ) - верхнего порога цены, при котором платежеспособный спрос становится равным нулю, то есть цены, при которой товар практически не будет востребован. Так же как и в случае с кривой предложения, при формировании функции спроса требуется задавать параметр (a), характеризующий особенности падения спроса при росте цены. При а =1 спрос уменьшается пропорционально увеличению цены (см. рисунок 5). 6 Рис. 5. Линейное уменьшение спроса при увеличении цены. При a>1 спрос эластичен и быстро падает с ростом цены (см. рисунок 6). Рис. 6. Быстрое падение спроса при росте цены. При a<1 спрос неэластичен и относительно медленно снижается при повышении цен (см. рисунок 7). 7 Рис. 7. Медленное падение спроса при росте цены. После того, как параметры функций предложения и спроса подобраны и поведение указанных кривых приведено в соответствие с экспертными оценками использующего модель экономиста, можно переходить к оптимизации плана закупок и продаж дефицитного товара. Для этого следует использовать расчетные данные о маржинальной прибыли, возникающей при различных комбинациях цен закупки (см. рисунок 8). Как следует из представленных на рисунке данных, в диапазоне изменения возможных цен закупки от 0 до 400 маржинальная прибыль равна нулю. Это связано с тем, что при таких низких ценах закупка товара невозможно, что следует из параметров задания кривой предложения (минимальная цена v min=400 ). При ценах закупки, начиная с 900, маржинальная прибыль отрицательна. Это связано с тем, что цены распродажи полученного объема дефицитного товара оказываются меньше цен закупки. Например, при цене 900 объем предложения составит 2083 условных единицы товара (при такой высокой цене поставщик готов на все). При этом расчетная цена полной распродажи такого объема товара при данной кривой спроса составит всего 815,35, что меньше цены закупки. Поэтому при тако цене закупки посреднику гарантированы убытки. Если только он не продаст часть товара по более высокой цене, а нераспроданный товар оставит на складе в надежде более выгодно перепродать его в последующем. 8 Рис. 8. Анализ маржинальной прибыли на всем диапазоне возможного изменения цен закупки дефицитного товара. В диапазоне цен закупки от 500 до 800 посредник при распродаже товара уравновешивает спрос и предложение при отпускных ценах, превышающих цену закупки и потому получает положительную маржинальную прибыль. Наиболее высокое значение маржинальной прибыли обеспечивается при цене закупки 700. В этом случае весь товар может быть распродан по цене 1089,21, а маржинальная прибыль составит 291906. Таким образом, необходимо более внимательно изучить последствия приобретения товара по цене примерно от 650 до 750 за единицу. Для этого в ячейку B13 следует ввести значение начальной цены равное 650 и указать шаг изменения цены 10 (см. рисунок 9). 9 Рис. 9. Анализ маржинальной прибыли в диапазоне оптимального изменения цен закупки дефицитного товара. Из представленных на рисунке данных видно, что оптимальной ценой закупки является 710. В этом случае можно получить 801 условную единицу товара, который может быть распродан полностью при цене 1075,52. В результате маржинальная прибыль от продажи товара составит 292778. Однако совершенно очевидно, что полученные расчеты весьма условны и вряд ли в точности оправдаются. Однако использование модели показывает, что если функции предложения и спроса построены более-менее верно, то следует ориентироваться на диапазон цен закупки от 680 до 740, в котором маржинальная прибыль изменяется относительно незначительно. Если в ходе переговоров с поставщиком выяснится, что при предлагаемых ему ценах он готов поставить товар в объемах, примерно соответствующих расчетным, то сделку надо заключать. В противном случае изменением параметров следует "подогнать" функцию предложения к выявленным значениям и повторить расчеты. Возможно, скорректированная модель даст другие результаты и укажет на другой оптимальный диапазон цен закупки-продажи. В этом случае следует провести следующую итерацию переговорного процесса. И так далее, до полного согласования. Кроме того, получив оценки оптимального плана нужно проверять их на устойчивость к возможной неточности в оценках кривых предложения и спроса. Для этого нужно задавать их небольшие изменения и проанализировать насколько сильно изменились оптимальные оценки цен, объемов предложения, спроса и маржинальной прибыли. 10