Время выполнения заданий (части А и B) 160 минут. Часть А

T171
Вариант 5
Время выполнения заданий (части А и B) — 160 минут.
Часть А
Задания A1-A30
При выполнении заданий A1—A20 в бланке ответов найдите номер выполняемого задания и
отметьте клеточку, номер которой соответствует номеру выбранного вами ответа, в соответствии с
образцом на бланке.
½
y + x2 = 0,
y = |x| ?
1 одно 2 два 3 три 4 четыре или больше 5 решений нет
1. Сколько решений имеет система
2. А.Попович срубил З.Горынычу 60% всех голов, однако на 70% всех оставшихся свободными
шей выросли по 4 новых головы на каждой. На сколько процентов увеличилось общее
количество голов на всех шеях З.Горыныча? Укажите остаток от деления этого числа на 5.
1 1 2 2 3 3 4 4 5 0
25x + 5y
2x + 5y
3. Если
= 3, то дробь
равна
x + 4y
4x − 6y
1 1 2 2 3 3 4 4 5 5
µ
¶
q
√
11π
4. Если a = sin
, то значение выражения a2 − 5a + 1 − a2 − 2a + 1 равно
6
1 0,5 2 1 3 1,5 4 2 5 2,5
πx
πx
5. Укажите наименьший корень уравнения sin
+ cos
= 0 принадлежащий отрезку
4
4
0 6 x 6 8.
1 1 2 3 3 5 4 7 5 2
¡
¢¡
¢
6. Значение выражения 63 log(16√2) 9 log(27√3) 8 равно натуральному числу, остаток от деления
которого на 5 равен
1 1 2 2 3 3 4 4 5 0
7. Больший корень уравнения
(x + 2)(x + 3)(x + 4)
= 0 равен
x−3
1 3 2 −2 3 −3 4 −4 5 2
8. Если число x равно корню уравнения 10 · 3x + 2 · 3x+1 = 81 · 2x , то
1 x ∈ (−999; 1,3)
2 x ∈ [1,3; 2,3) 3 x ∈ [2,3; 3,3) 4 x ∈ [3,3; 4,3) 5 x ∈ [4,3; 999)
√
9. Наименьшее значение функции f (x) = x − 10 x равно
1 −24 2 −25 3 −5 4 −12,5 5 −100
10. Если число d равно растоянию на числовой оси между двумя корнями уравнения
25−x − 8 · 15−x + 15 · 9−x = 0, то
1 d ∈ (0; 0,6)
2 d ∈ [0,6; 1,1) 3 d ∈ [1,1; 1,6) 4 d ∈ [1,6; 2,1) 5 d ∈ [2,1; 999)
1
1
1
11. Производная функции f (x) = x + + x2 + 2 + x3 + 3 в точке x = 1 равна
x
x
x
1 6 2 −3 3 2 4 0 5 12
√
12. Найдите сумму всех различных корней уравнения log3 3 x + logx 9 = 53 и укажите остаток от
деления этого натурального числа на 5.
1 1 2 2 3 3 4 4 5 0
Олимпиада 2008
T171
Вариант 5
13. Если число X равно наименьшему положительному корню уравнения
cos2 (4x) + cos2 (12x) − cos(8x) cos(38x) = 1, то значение выражения πX −1 равно натуральному
числу, остаток от деления которого на 5 равен
1 1 2 2 3 3 4 4 5 0
14. Прямая, касающаяся графика функции y = (x − 4)3 + 100 в точке с абсциссой x = 3,
пересекает ось ординат в точке (0; Y ), причем Y — натуральное число, остаток от деления
которого на 5 равен
1 1 2 2 3 3 4 4 5 0
15. Наибольшее значение параметра p, при котором уравнение 8x − 18 · 4x + 15 · 2x+2 = p имеет
ровно два различных корня, равно натуральному числу, остаток от деления которого на 5 равен
1 1 2 2 3 3 4 4 5 0
16. В начале 2001 года Билл положил 32 у. е. в банк. В начале 2003 года он обнаружил, что за
два года сумма на его счету стала больше на 40 у. е.. В начале какого года он в первый раз
обнаружит на своем счету сумму, которая будет больше 200 у. е., если начисленные проценты
прибавляются ко вкладу в конце каждого года и условия помещения капитала в этот банк не
меняются?
1 2004 2 2005 3 2006 4 2007 5 2008 или позже
17. Сумма всех различных значений параметра p, при которых уравнение
x2 − 2px + p2 + p − 20
= 0 имеет единственный корень, равна натуральному числу, остаток от
x
деления которого на 5 равен
1 1 2 2 3 3 4 4 5 0
18.
r Найдите2сумму всех целочисленных решений неравенства
2x + 2 x − 7x + 10 p
·
· (8 − x)(x + 6) 6 0 и укажите в ответе остаток от деления
x − 3 (x − 7)(x − 5)
полученного числа на 5.
1 1 2 2 3 3 4 4 5 0
19. Произведение всех различных корней уравнения
p
2 log3 |x − 7| − log3 |x| + 5 = log3 |x| − 2 log3 |x − 7| + 7
равно натуральному числу, остаток от деления которого на 5 равен
1 1 2 2 3 3 4 4 5 0
20. В треугольнике ABC проведена биссектриса CM, причем BC = 9, AC = 6, M B = 3.
Прямая, проходящая через точку C, пересекает прямую AB в точке N, причем отрезок CB
совпадает с биссектрисой треугольника CM N . Пусть число x равно длине отрезка BN .
Укажите верное утверждение.
1 x ∈ (0; 3,2)
2 x ∈ [3,2; 4,4) 3 x ∈ [4,4; 5,6)
4 x ∈ [5,6; 6,8) 5 x ∈ [6,8; 999)
Олимпиада 2008
Т 171
Вариант 5
Задания А 21 – А 30
Выберите среди предложенных ответов свой единственный и отметьте соответствующую
ему цифру в бланке ответов на пересечении номера вопроса и номера ответа.
21. Какое максимальное разрешение экрана возможно для размещения 15-цветного
изображения при величине видеопамяти 150 Кбайт?
1) 800 x 600
2) 1024 x 768
3) 640 x 480
4) 1280 x 1024
5) 320 x 240
22. Восьмеричное число 576.12 в шестнадцатеричной системе счисления равно:
1) 17E.12
2) 17C.1
3) 10D.01
4) 11A.12
5) 17E.28
23. Даны два числа: десятичное число А= -322 и восьмеричное число В=-34. В основной
памяти ЭВМ эти числа представлены в формате с фиксированной точкой в дополнительном
коде. Длина формата – 16 двоичных разрядов. Выполнить операцию А+В в формате с
фиксированной точкой и определить шестнадцатеричный дополнительный код результата
операции.
1) FEA2
2) FEA3
3) CEA2
4) FCA2
24. Результатом минимизации логической функции F=(NOT x1 OR NOT x2 OR NOT (x1 AND
NOT x2)) AND x2, где AND, OR и NOT – знаки логических операций конъюнкции, дизъюнкции
и отрицания соответственно, является формула
1) NOT x1 AND x2
2) x2
3) x1
4) x1 OR NOT x2
5) x1 OR x2
25. Логической функции F от трех переменных, принимающей значение "истина" на наборе
значений переменных F(4) соответствует следующая аналитическая форма представления:
1)(NOT x1 AND NOT x2 AND NOT x3) OR (NOT x1 AND NOT x2 AND x3) OR (NOT x1 AND
x2 AND x3)
2)(NOT x1 AND x2 AND NOT x3) OR (NOT x1 AND x2 AND x3)
3)(NOT x1 AND NOT x2 AND x3) OR (NOT x1 AND x2 AND NOT x3) OR (NOT x1 AND x2
AND x3)
4)(NOT x1 AND NOT x2 AND NOT x3) OR (NOT x1 AND NOT x2 AND x3) OR (NOT x1 AND
x2 AND NOT x3) OR (NOT x1 AND x2 AND x3)
5) x1 AND NOT x2 AND NOT x3
Олимпиада 2008
Т 171
Вариант 5
26. Истинность двух высказываний: "неверно, что если виноват водитель А, то виноват и
водитель В" и "неверно, что если виноват водитель А, то виноват и водитель С" означает, что
виноваты водители
1) С
2) А,В
3) А,В,С
4) А
5) А,С
27. Начальное состояние схемы с памятью приведено на рисунке. Какие логические сигналы
необходимо установить на входах A,B,C, чтобы на выходах Y и Z были получены логические
сигналы: Y=1 ,Z=1?
A
0
ИЛИ
Y
0
И
НЕ
И
НЕ
C
1
ИЛИ
B
НЕ
1
0
Z
1) A=1, B=0, С=0
2) A=0, B=1, С=1
3) A=0, B=1, C=0
28. Определены переменные A,B,C,D,F типа “Множество”: A={3,B,X,E},
B={S,C,X,E},С={S,3,D,X},D={4,D,X,E}.Определить значение F = (A U B) ^ (С U D), где ^ - знак
операции пересечения, а U – знак операции объединения множеств.
1) Пустое множество
2) {3,X}
3) {X,E}
4) {S,3,X,E}
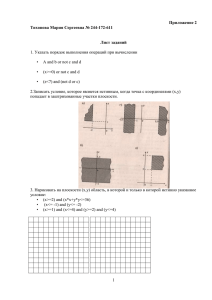
29. Высказывания А, В, С истинны для точек, принадлежащих кругу, треугольнику и
прямоугольнику соответственно. Приведена формула (B and not A) or (A and not B)
определяющая геометрическое место точек. Определите фигуру на приведенных ниже
рисунках, которая соответствует данной формуле.
А)
Б)
Олимпиада 2008
Т 171
Вариант 5
В)
Г)
1) А
2) Б
3) В
4) Г
30. Активной ячейкой электронной таблицы является ячейка:
1) на которой находится курсор;
2) содержащая какое-либо значение;
3) на которую есть ссылка в формуле;
4) содержащая формулу.
Олимпиада 2008
T171
Вариант 5
Часть B
Задания B1-B10
Ответом на задания В1-В5 должно быть некоторое целое число или число, записанное в
виде десятичной дроби. Это число надо записать в бланк ответов справа от номера
выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус для
отрицательного числа и запятую в записи десятичной дроби пишите в отдельной клеточке
Единицы измерений, а также символ процента писать не нужно.
1. Найдите сумму всех различных целочисленных значений параметра p, при
√
2
4
которых уравнение (p − 16p + 55)x − 6 3x4 + 1 = 0 имеет ровно два различных
корня.
2. Найдите наименьшее
½ (или единственное) значение2 параметра p, при котором
x log2 (p − 3) + y log2 (p − 1) = q + 3 + 3y,
система уравнений
имеет бесконечное
x − y = 4q
множество решений решений хотя бы для одного значения параметра q.
3. Требуется изготовить будку для собаки в форме прямоугольного
параллелепипеда из трех листов фанеры, причем пол и две боковые стенки делать
не нужно, так как будка будет стоять в углу двора у забора, и к тому же одна из
боковых стенок должна быть обязательно квадратной. Стоимость 1 кв м фанеры,
идущей на боковые стенки, равна 2 у. е., стоимость 1 кв м потолочного листа
равна 1 у. е. Найдите наименьшую стоимость фанеры (в у. е.), при которой обьем
будки будет равен 972 куб м.
4. В начале 2001 года Билл сделал в банк А вклад, равный 65 у. е. Годовая
процентная ставка этого банка равна 8%. Джек в то же время сделал вклад в тот
же банк на ту же сумму. В начале каждого следующего года Билл снимает со
своего счета 2 у. е. и передает Джеку, который немедленно кладет эту сумму на
свой счет. На сколько процентов в начале 2301 года вклад Джека будет больше
вклада Джека? В ответе укажите ближайшее к точному ответу натуральное
число.
5. Найдите
наименьшее значение¯ параметра p, при котором система уравнений
(
¯
¯ 3
¯
|y| = ¯|x| − 18x2 + 96|x| − 128¯,
имеет ровно 12 различных решений.
|9x| + |y| = p
Олимпиада 2008
Т 171
Вариант 5
Задания В 6 – В 10
Выполните задание и внесите краткий ответ в бланк ответов В справа
от соответствующего номера задания.
6. Вычислить сумму шестнадцатеричного числа А=F1A.8 и двоичного числа В=1010.101.
Результат представить в восьмеричной системе счисления. При записи ответа целую и дробную
часть числа разделите символом точки
7. В специализированной ЭВМ целые числа рассматриваются как числа со знаком и
представляются в виде дополнительного кода. Для хранения кода может выделяться ячейка
памяти длиной 16 бит (слово) или 8 бит (полуслово). В ячейку памяти X длиной в слово занесен
шестнадцатеричный код E03F, после чего выполнен циклический сдвиг кода влево на 2 бита.
После сдвига копия ячейки X размещается в двух ячейках длиной полуслово каждая. В ячейку
A занесены младшие восемь бит из ячейки X, а в ячейку B – старшие восемь бит из ячейки X.
Определите, какое десятичное число представлено кодом, который хранится в ячейке B.
8. Какие логические сигналы будут получены на выходах R,Q,S,Z комбинационной схемы, если
на входы схемы поданы сигналы: a=1, b=0, c=1, d=0 ? В ответе значения выходных сигналов
укажите в последовательности R,Q,S,Z
a
И
b
c
М2
ИЛИНЕ
ИЛИ
R
ИЛИ
Q
И-НЕ
d
ИЛИ
S
И
И
М2
Z
ПРИМЕЧАНИЕ: элемент М2 реализует логическую функцию сложения по модулю два
(отрицание равнозначности)
Ответ:
R=___ Q=___ S=___ Z=___
9. Определите значение, которое будет выведено выполнении программы, исходный код
которой приведен ниже
Вариант на языке Pascal
program PR;
const n = 6;
const m = 3;
type MAS=array[1..n,1..m] of integer;
Олимпиада 2008
Т 171
Вариант 5
function f(a,b:integer):integer;
begin
if a < b then
f := a
else
f:=b
end;
var a:MAS;
i,j,s,k:integer;
begin
k := 1;
for i:=n downto 1 do
for j:=m downto 1 do
begin
a[i,j] := k mod 4;
k := k +1;
end;
s := 0;
for i:=1 to n do
s := s + a[i,f(n,m)];
write('s=',s);
end.
Вариант на языке C
#include <stdio.h>
#define N 6
#define M 3
int f(int a,int b)
{
if(a<b) return a;
else
return b;
}
void main()
{
int a[N][M], i, j, s,k;
for (i = N-1,k=1; i>=0; i--)
for (j = M-1; j>=0; j--,k++)
a[i][j] = k % 4;
for (s=i=0; i<N; i++)
s = s + a[i][f(N,M)-1];
printf("s = %d",s);
}
Вариант на языке Basic
DECLARE FUNCTION F! (a!, b!)
n = 6: m = 3
DIM a(n, m)
k = 1
FOR i = n TO 1 STEP -1
FOR j = m TO 1 STEP -1
a(i, j) = k MOD 4
k = k + 1
NEXT j
NEXT i
s = 0
FOR i = 1 TO n
s = s + a(i, F(n, m))
NEXT i
PRINT "s = "; s
FUNCTION F (a, b)
IF a < b THEN
F = a
ELSE
F = b
END IF
END FUNCTION
Олимпиада 2008
Т 171
Вариант 5
10. Определите значение, которое будет выведено после выполнения алгоритма, приведенного
на рисунке. Знаком mod обозначена операция вычисления целочисленного остатка, а знаком div
– операция целочисленного деления
Вход F(X,K)
Начало
B:=0
A:=X
J:=1
A:= 472465
X1:=A mod 1000
X2:=A div 1000
Да
Нет
A>0
X1:=F(X1,2)
C:= A mod 10
A:= A div 10
Возврат B
X2:=F(X2,3)
Да
C>3
B:=X2 * 1000
B:=B + X1
Вывод B
Нет
0
J mod K
≠0
B:= B*10 + С
J:=J + 1
B:=B*10 + (C-1)
J:=J + 1
Конец
Олимпиада 2008