Статическая устойчивость Предел мощности при приемной

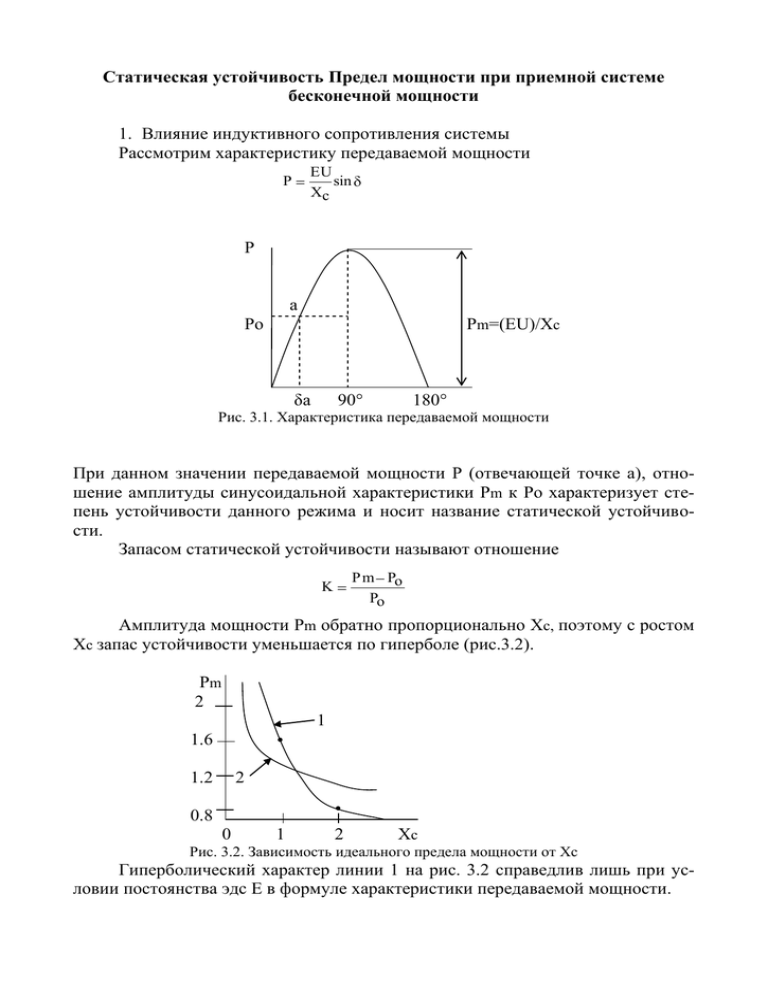
Статическая устойчивость Предел мощности при приемной системе
бесконечной мощности
1. Влияние индуктивного сопротивления системы
Рассмотрим характеристику передаваемой мощности
EU
sin
Xc
P
P
a
Po
Pm=(EU)/Xc
δa
90°
180°
Рис. 3.1. Характеристика передаваемой мощности
При данном значении передаваемой мощности Р (отвечающей точке а), отношение амплитуды синусоидальной характеристики Рm к Ро характеризует степень устойчивости данного режима и носит название статической устойчивости.
Запасом статической устойчивости называют отношение
Pm Po
Po
K
Амплитуда мощности Pm обратно пропорционально Xc, поэтому с ростом
Xc запас устойчивости уменьшается по гиперболе (рис.3.2).
Pm
2
1
1.6
1.2
2
0.8
0
1
2
Xc
Рис. 3.2. Зависимость идеального предела мощности от Xc
Гиперболический характер линии 1 на рис. 3.2 справедлив лишь при условии постоянства эдс Е в формуле характеристики передаваемой мощности.
В действительности, при увеличении Xc при неизменных, передаваемых в
систему, активной и реактивной мощности, эдс Е увеличивается (рис.3.3).
E'
I X 'c
Е
I Xc
δ
φ
U
I
E'
Рис. 3.3. Увеличение эдс
при увеличении
X 'c
'
При увеличении эдс E идеальный предел мощности должен увеличиваться, поэтому зависимость идеального предела мощности от Xc отклоняется
от гиперболы (кривая 1 на рис 3.2) и становится более пологой (кривая 2 на рис.
3.2).
Рассмотрим индуктивные составляющие системы. Для ЛЭП 220 кВ длиной 200 км с генератором без АРВ относительные значения индуктивных сопротивлений распределяются следующим образом. Если синхронное индуктивное сопротивление генератора принять за единицу, то на сопротивление каждого из трансформаторов (повышающего и понижающего) по 0.13 единиц, на
ЛЭП – 0.25ед. Таким образом, синхронное индуктивное сопротивление генератора имеет наибольший вес. Следует отметить, что при приведении индуктивного сопротивления линий к напряжению генератора оно уменьшается в к2 раз,
где к – коэффициент трансформации. За счет уменьшения относительного сопротивления линии при увеличении напряжения, зависимость Хс = f(U) имеет
нелинейный характер.
Х
Pm
Хл
Pm при Хл=0
Pm
Xг+Хт
U
Рис 3.4. Изменение амплитуды характеристики мощности
при увеличении напряжения линий
U
Xг
EU
X л X тр
Рассмотрим влияние шунтирующего сопротивления на амплитуду характеристики мощности. Дана электропередачa
E
E
Л1
Л2
U
Xг
Xл1
Xл2
U
Xр
P
Рис.3.5 Электропередача и ее схема замещения
Обозначим через Х1= Хг+Хл1, Х2=Хл2, Х3=Хр, тогда схема принимает
вид:
Е
Х1
Х2
U
Х3
В связи с тем, что в схеме находятся только реактивные сопротивления,
углы потерь α =0:
90 o
90 o
90 o
0
В связи с этим уравнение для активной мощности, которую генератор отдает в сеть
E 2 y11 sin 11
Pг
EUy 12 cos
12
принимает вид
Pг
EUy12 sin
EU
sin
X12
Для нахождения Х12 преобразуем звезду (Y) сопротивлений Х1, Х2, Х3 в
треугольник (Δ) и найдем Х12:
X12
X1 X2
X1X2
X3
Если Х3 отключено, то Х12 = Х1 + Х2.
Очевидно, что при включении реактора сопротивление Х12 увеличивается, следовательно, Pm уменьшается.
P
Pm=(EU)/(Х1+Х2)
без реактора
Pm1=(EU)/(X1+Х2+Х1Х2/Х3)
с реактором
0
90°
180°
δ
Характеристики мощности при изменении эдс
Рассмотренные ранее примеры построения характеристик мощности
осуществлялись при неизменной эдс. Вместе с тем, при увеличении угла δ, связанное с ростом передаваемой мощности, приводит к уменьшению напряжения
генератора. Если возрастание нагрузки происходит достаточно медленно, то
эдс генератора путем регулирования тока возбуждения можно изменить. При
этом предел передаваемой мощности резко увеличивается.
В настоящее время имеется два типа автоматического регулирования возбуждения (АРВ) – сильного действия и пропорционального действия. В том и
другом случае эдс генератора увеличивается.
АРВ сильного действия дают возможность поддерживать практически
постоянное напряжение на шинах генератора или на стороне высшего напряжения трансформатора. Это служит основанием вводить синхронный генератор
схемой замещения при U=const и хг = 0.
АРВ пропорционального действия поддерживает близкой к постоянной
величине эдс E'q. С АРВ пропорционального действия синхронный генератор
учитывается переходной эдс E'q и индуктивным сопротивлением x'd.
Будем считать, что понижение напряжения происходит плавно, и ток возбуждения увеличивается таким образом, что напряжение Uг остается неизменным.
Рассмотрим схему электропередачи.
U
Г
Тр1
ЛЭП
Тр2
Хл
Хт2
Е
Хг
Хт1
U
Хтл
Рис. 3.6. Электропередача и схема замещения
Построим векторную диаграмму
С'
E'
Е
С
В'
U'г
δ'
О
δ
φ
I Xг
В
I Xлт
Uг
I
А
Рис.3.7. Векторная диаграмма схемы электропередачи при изменении угла δ
Если увеличить угол δ до δ' при одной и той же величине эдс Е, то очевидно, что напряжение генератора уменьшается с величины Uг до величины
U'г. Положение точки В' находится из пропорции АВ/АС = АВ'/АС'.
При наличии у генераторов АРВ регуляторы, реагируя на понижение напряжения генератора, будут увеличивать ток возбуждения таким образом, чтобы напряжение генератора Uг оставалось неизменным. Построим векторные
диаграммы для нескольких углов δ, и для каждого угла определим эдс Е и построим соответствующие характеристики мощности.
Е'' С''
Е'
С'
U'г
В' Е
В''
U''г
δ'
С
В
Uг
δ
О
А
Рис.3.7. Векторная диаграмма схемы электропередачи при изменении угла δ
и постоянном напряжении генератора
P
Po
0
δ0
90°
180°
δ
Рис. 3.8 Характеристики мощности при постоянстве напряжения генератора
Из векторной диаграммы следует, что предельное значение мощности
достигается не при δ =90°, а при δг =90°, где δг – угол между напряжением системы и напряжением генератора.
Запас устойчивости увеличивается и может быть ограничен характеристиками возбудителя. При срабатывании регулятора напряжение возбудителя
генератора растет не беспредельно, а ограничивается некоторым максимальным
значением – потолком возбуждения. Если потолок возбуждения достигнут при
угле, меньшем 90°, то при дальнейшем росте угла δ процесс протекает при постоянстве эдс.
Если бы регуляторы (пропорционального действия или сильного действия) обладали идеальной чувствительностью, то предельный режим определялся бы амплитудой внешней характеристики (жирная линия), достигаемой при
углах, значительно больших 90°.
Неизбежное запаздывание в изменении тока возбуждения возбудителя и
генератора, приводит к тому, что генератор может работать при углах в районе
90°, но не достигающих значений, при которых характеристика мощности имеет максимальное значение.
Действительный предел мощности
Для электропередачи, состоящей из генератора, элементов системы электроснабжения (трансформаторов, ЛЭП) и шин приемной системы было установлено, что при постоянстве эдс и увеличении угла δ напряжение уменьшается
на всех промежуточных элементах схемы.
Если приемная система представлена нагрузкой и местной электростанцией, то при оценке статической устойчивости следует исходить из постоянства
эдс Е1 и Е2. Увеличение угла δ12 между эдс Е1 и Е2 или угла δ между эдс Е1 и
напряжением системы U по прежнему сопровождается уменьшением напряжения на элементах схемы, а следовательно и на шинах нагрузки.
Если при построении характеристики передаваемой мощности исходить
из зависимости
P
E1U
sin
Xc
где Хс – индуктивное сопротивление электропередачи между Е1 и напряжением
на шинах нагрузки U.
Напряжение на шинах нагрузки U следует считать переменным и при
увеличении δ оно уменьшается. Характеристика мощности имеет падающий
характер.
P
100%
Pmд
Po
80%
а
60%
40%
0
δ0
90°
180°
δ
Рис. 3.9 Характеристики мощности при уменьшении напряжения нагрузки
Характеристика мощности имеет падающий характер. Действительный
предел мощности Pmд получается меньше идеального. Таким образом, снижение напряжения нагрузки ухудшает статическую устойчивость системы. В
практических расчетах устойчивости характеристику передаваемой мощности
часто строят не в зависимости от угла δ, а от напряжения.
U
U
а
в
100%
а
в
Po
Рm ид
100%
Po Pmд
Рm ид
Pmд
Рис. 3.10 Характеристики мощности U=f(P) и действительный предел мощности Pmд
Очевидно, что чем меньше падает напряжение нагрузки с ростом передаваемой мощности и угла δ, тем более высоким получается действительный предел мощности. Уменьшение индуктивных сопротивлений генераторов и элементов электропередачи способствует стабилизации напряжения нагрузки.
Влияние нагрузки на напряжение в точках ее приложения называется регулирующим эффектом нагрузки..
Действительно, снижение напряжения на нагрузке приводит к уменьшению активных и реактивных мощностей. Уменьшение потоков мощностей в сети, питающих нагрузку, уменьшает падение напряжения на элементах электропередачи, что в некоторой мере поддерживает напряжение. Значительно боль-
шее влияние при этом оказывает степень изменения реактивной мощности, поскольку падение напряжения на индуктивных сопротивлениях определяется
прежде всего реактивными токами.
Для решения задачи регулирующего эффекта нагрузки необходимо знать
статические характеристики – зависимости Pн = f(U), Qн =f(U). Касательные к
этим характеристикам dPн/dU и dQн/dU определяют регулирующий эффект
нагрузки.