154 Глава IV СТРОЕНИЕ АТОМА И ПЕРИОДИЧЕСКАЯ

Глава IV
СТРОЕНИЕ АТОМА И ПЕРИОДИЧЕСКАЯ
СИСТЕМА ЭЛЕМЕНТОВ
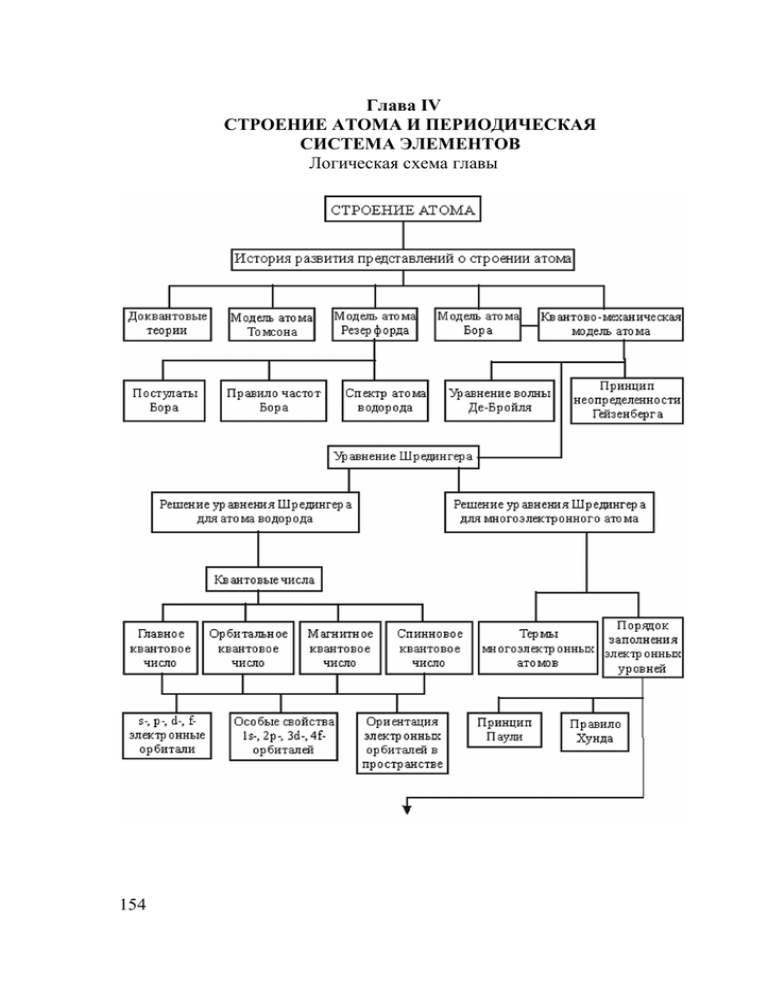
Логическая схема главы
154
155
Строение атома
Атом представляет собой очень сложную систему, состоящую из
ядра и электронной оболочки. Ядро составляют нейтроны и протоны. В
химии не изучают ядра атомов, но, тем не менее, ниже мы рассмотрим
некоторые характеристики ядер. Ядра атомов – предмет изучения ядерной физики. Мы же будем рассматривать ядро как единое целое, а атом
как частицу, состоящую из ядра и электронной оболочки.
Мысль о существовании элементарного электрического заряда возникла еще в XVIII в. В работах Б. Франклина, В. Вебера, Г. Деви и других. можно найти указание на существование "электрического атома".
Очень важными для подтверждения существования электрического заряда явились законы электролиза, открытые М. Фарадеем в 1830 г. Анализ этих законов привел Г. Гельмгольца к идее элементарного электрического заряда. Гельмгольц писал: "Если мы допускаем существование
химических атомов, то мы вынуждены заключить отсюда, что и электричество разделяется на определённые элементарные количества, которые играют роль атомов электричества". Термин "электрон" предложен английским физиком Дж. Стони. Он писал: "В каждом химическом
атоме может быть несколько элементарных зарядов. Эти заряды, которые удобно назвать "электронами", не могут быть отделены от атомов,
но они обнаруживаются, когда атомы вступают в химическое соединение".
В 1897 г. гипотеза об электронах получила экспериментальное подтверждение в работах Э. Вихерта и Дж. Дж. Томсона.
Вопрос о том, как располагаются ядро и электроны в атоме и каково строение ядра волновали умы многих ученых. Но только в начале XX
в. появились различные модели, изображающие строение атома, которые каким-то образом объясняли свойства атомов. В 1904 г. Томсоном
была предложена модель, согласно которой электроны располагались в
атоме как изюм в булке. Взаимное отталкивание электронов обеспечивало их равномерное распределение в атоме. Таким образом достигался
контакт между положительными и отрицательными зарядами. Ионизацию можно было представить как вырывание электрона из атома, в результате чего оставался твердый массивный атом с положительным зарядом. Теорию Томсона сменила планетарная модель атома Резерфорда
(1911). Согласно этой теории в центре атома располагалось тяжёлое
массивное ядро, вокруг которого, как планеты вокруг Солнца, вращались электроны. Но эта модель просуществовала недолго и имела ряд
156
очень существенных недостатков: модель не объясняла, во-первых, почему электроны при движении по орбите не теряли энергию и не падали
на ядро; во-вторых, не объясняла дискретного спектра излучения атомов.
Резерфорд отлично видел недостатки своей модели атома. Он предупреждал, что «вопрос об устойчивости предлагаемого атома на этой
стадии не следует подвергать рассмотрению. Устойчивость окажется,
очевидно, зависящей от тонких деталей структуры атома и движения
составляющих его заряженных частей».
В конце XIX в. – начале XX в. в физике было сделано множество
открытий. Были открыты ядра атомов, α-частицы, β-частицы, γизлучение, квантовая теория света, теории Эйнштейна, рентгеновского
излучения и другие, которые показали сложность строения атома и привели к убеждению, что законы классической физики нельзя применять к
изучению и описанию свойств микрочастиц. Сложилась парадоксальная
ситуация, когда эксперимент указывал на справедливость планетарной
модели атома, а по известным тогда законам физики такой атом не мог
существовать. Выход из этого положения был найден молодым датским
физиком Нильсом Бором.
В 1913 г. Н. Бор предложил свою модель строения атома с использованием квантовой теории света Планка и планетарной модели Резерфорда.
В основе модели атома Бора лежат два постулата:
1. Электрон вращается вокруг ядра, не излучая энергии, по
строго определенным стационарным орбитам.
Движение какого-либо объекта вокруг центра в классической механике определяется моментом количества движения mvr. Согласно квантовой механике, энергия такого объекта может иметь только определенные значения и изменяться скачками. Бор считал, что момент
количества электрона должен квантоваться, т. е. должен быть равен целому числу квантов действия:
mvr = n( h/2π),
(1)
где n = 1,2,3...; h – постоянная Планка;
h = 6,625 ⋅ 10-27 эрг ⋅ с = 6,62 ⋅ 10-34 Дж ⋅ с.
Из (1) следует, что минимальная энергия электрона соответствует n
= 1. Это состояние для атома водорода называется основным. Состояния с n = 2,3,4... называются возбужденными.
157
При вращении электрона вокруг ядра центробежная и центростремительная силы уравновешены и
mv2/r = e2/r2.
(2)
Из (1) и (2) можно найти
r = (n2h2)/(π2me2z).
(3)
Для z = 1, т.е. для атома водорода
r = (n2h2)/(4π2me2);
v = (2πe2)/(hn);
v = e2/hn.
(4)
(5)
(6)
Расчёты показывают, что при
r1 = 0.53Å
r2 = 2.12 Å
r3 = 4.77 Å
n=1
n=2
n=3
v1 = 2200 км/с;
v2 = 1093 км/с;
v3 = 792 км/с.
2. При переходе с одной орбиты на другую электрон поглощает
или излучает квант энергии. При возбуждении атома, т.е. при переходе электрона на возбужденный уровень, происходит поглощение кванта
энергии:
E1 – E2= hν.
(7)
Уравнение 7 называют правилом частот Бора.
Энергию электрона в n-стационарном состоянии можно рассчитать
по уравнению
En – En-1 =(me4z2)/(2ћ)(1/nn-12 – 1/nn2) =
= (me4/2ћ) ⋅ (z2/n2)=13,6z2/n2,
(8)
где ћ = h/2π.
Для атома водорода при z = 1 и n = 1 Е = 13.6 эВ. Из уравнений (7)
и (8) можно получить уравнение для расчета спектральных линий:
E1.2 = (me4z2)/(2ћ2) ⋅ (1/n12 – 1/n22) = hν,
а для атома водорода:
E = (me4)/(2ћ2) ⋅ (1/n12 – 1/n22)=hν.
Отсюда
158
(9)
ν = (me4)/(4πћ3) ⋅ (1/n12 – 1/n22),
где (me4)/(4πћ3) = R – постоянная Ридберга для описания линий спектра
атома водорода в видимой области (серия Бальмера). Константа Ридберга входит в формулу Бальмера для расчёта спектральных линий в видимой части спектра атома водорода:
ν =сR
n
k 
где ν – частота излучения; с – скорость света, n и k – целые числа: n = 2,
k = 3,4,5,6 ...; R – константа Ридберга (R = 109977,575 см-1).
Рассчитанная из уравнения (9) постоянная Ридберга дает хорошее
совпадение с экспериментальной величиной.
Полная энергия электрона складывается из кинетической и потенциальной
E =(mv2)/2 – e2/r = (mv2)/2 – mv2= – (mv2)/2,
Отсюда видно, что полная энергия электрона равна его кинетической
энергии, взятой с обратным знаком.
Бор рассчитал спектр атома водорода, который образуется при переходе электронов между уровнями. Переходу на уровень с n = 1 соответствует серия спектральных линий, называемая серией Лаймона:
n1 = 1
n2 = 2,3,4...
K – серия
Серия Лаймона (1915)
λ = 1500 Å
Переходу на уровень с n = 2 соответствует серия спектральных линий Бальмера:
n1 = 2
n2 = 3,4,5...
Серия Бальмера (1885)
видимая часть света.
λ = 4000 – 6000 Å
Переходам на уровень с n = 3 соответствует серия Пашена:
n1 = 3
n2 = 4,5,6...
Серия Пашена, ИК-область
Серии Бреккета соответствуют переходы на уровень n = 4:
n1 = 4
n2 = 5,6,7...
Серия Бреккета.
159
Серия спектральных линий, соответствующая переходам на уровень
со значением квантового числа n = 5, была предсказана Бором и открыта
в 1924 г. Пфундом:
n1 = 5
n2 = 6,7...
Серия Пфунда (1924).
Полученные расчетные данные совпали с известными экспериментальными. Таким образом, модель атома Бора объяснила спектр атома
водорода.
Достоинства модели Бора
Модель Бора имела следующие достоинства:
1) доказала неприменимость законов классической физики к изучению атома;
2) доказала наличие стационарных состояний в атоме, при которых
не происходит излучения;
3) объяснила дискретность излучения атома;
4) показала сложность строения атома;
5) с помощью модели Бора рассчитан и объяснен спектр только
атома водорода.
Но у модели Бора было несколько существенных недостатков:
1) не вскрыла сущность процессов, происходящих в атоме;
2) не сформулировала законы, согласно которым электрон движется в атоме;
3) не объяснила, как переходит электрон с одной стационарной
орбиты на другую;
4) не объяснила тонкую структуру атомов;
5) c ее помощью рассчитали спектр только атома водорода и водородоподобных атомов, т.е., атомов, содержащих только один электрон: Li2+, Be3+, B4+. При расчете спектральных линий других атомов
были получены результаты, не совпадающие с экспериментальными.
Линии, наблюдаемые в спектре атома лития, удалось объяснить, только
предположив, что каждый из боровских энергетических уровней, кроме
первого, представляет собой совокупность подуровней с различными
энергиями: два подуровня для n = 2, три подуровня для n = 3, четыре
подуровня для уровня с n = 4 и т.д. Различные подуровни, соответствующие одному значению квантового числа n, обозначают буквенными
символами, основанными на характерном виде спектральных линий,
которые соответствуют этим подуровням. Так, символ s происходит от
160
слова sharp (резкий), символ р – от слова principal (главный), d – от
слова diffuse (диффузный), f – от fundamental (фундаментальный);
6) в своей теории Бор использовал как законы классической, так и
законы квантовой физики. На это указывал Бору ещё Резерфорд. Он писал Бору: «Ваши мысли относительно возникновения спектра водорода
очень остроумны и представляются хорошо продуманными, однако сочетание идей Планка со старой механикой создаёт значительные трудности для понимания такого рассмотрения... Мне кажется, Вы вынуждены предположить, что электрон заблаговременно знает, где
остановиться»;
7) теорию Бора оказалось невозможным применить для объяснения химической связи. Так, произведенный по этой теории расчет энергии разрыва связи в ионе H2+ дал отрицательную величину этой энергии,
т.е. показал, что такой ион не должен существовать. Но такой ион существует и является достаточно устойчивым: энергия связи около 240
кДж/моль;
8) в теории Бора все стационарные орбиты равноценны, отличаются друг от друга только величинами энергий и других физических
величин. В действительности же по своему физическому характеру они
существенно различны. В основном состоянии изолированный атом может находиться сколько угодно долго, а в возбуждённом – всего лишь
порядка 10-8 сек. Эта неравномерность состояний получило объяснение
только в квантовой теории атома.
Модель Бора в 1916-1924 гг. развил Зоммерфельд, который показал, что тонкую структуру атома можно объяснить, если допустить существование не только круговых, но и эллиптических орбит. Он ввел
понятие второго квантового числа, связанного с орбитальным движением электронов. Это позволило объяснить различие в энергии подуровней
с одинаковым главным квантовым числом n, возможностью проникновения электрона на эллиптической орбите в близкую к ядру область
(рис. 4.1). Для атома водорода, имеющего ядро с зарядом +1, энергии
всех подуровней с одинаковым n должны быть одинаковы. Но для атома
лития, в котором ядро с зарядом +3 экранируется двумя внутренними
электронами, третий внешний электрон испытывает притяжение эффективного заряда +1. Электрон же на эллиптической орбите проникает под
экранирующую оболочку и поэтому на части своей траектории испытывает действие положительного заряда +3. Отсюда следует, что сильно
вытянутые эллиптические орбиты будут обладать дополнительной стабильностью.
161
4t
3d
2p
2s
Ядро
4d
4p
3p
3s
4s
.n=2
1n=3
1n=4
Рис.4.1. Зоммерфельдовские орбиты
Наиболее эллиптичные из всех орбиталей s-орбитали, согласно модели Зоммерфельда, соответствуют наиболее стабильным среди всех
подуровням. В многоэлектронном атоме, ядро которого окружено экранирующими оболочками внутренних электронов, электроны на наиболее
вытянутых эллиптических орбиталях, проникающие через эти оболочки,
должны испытывать более сильное притяжение ядра. Поэтому такие
орбиты оказываются более стабильными и имеют меньшую энергию.
Так, 4р-подуровень должен располагаться ниже, чем 4f-подуровень.
Модель Зоммерфельда позволила продвинуться в объяснении атомных спектров лишь до щелочных металлов. Далее она тоже зашла в тупик. Последующие открытия потребовали замены модели Бора – Зоммерфельда более совершенной.
Двойственная природа микрочастиц
В 1924 г. французский физик Луи де Бройль предположил, что не
только излучение, но и материальные частицы обладают двойственной
природой, т. е. свойствами волны и частицы. Размышляя над природой
квантования, де Бройль предположил, что для электрона характерны
свойства электромагнитных волн, и для него можно рассчитать длину
волны. Кроме того, де Бройль предположил, что длина волны электрона
укладывается целое число раз на орбите, т.е. сопоставил её со стоячей
волной. Примером стоячей волны могут служить колебания скрипичной
струны, закрепленной на обоих концах. Струна может колебаться только
с определенными частотами. Когда волна колеблется как одно целое, то
издает основной тон, при колебаниях с более короткими длинами волн
издаются обертоны. Колебания с длиной волны, при которой амплитуда
не становится равной нулю на концах закрепленной струны, не могут
осуществляться (рис. 4.2).
162
1б)
1а)
A(x)
1λ=2α
1λ=4α
1λ=α
1λ=4/3α
1λ=2/3α
1λ=4/5α
1в)
1n=4
1г)
1n=4 3
1
Рис.4.2. Приемлемые (а) и неприемлемые (б) стоячие волны, приемлемые (в) и
неприемлемые (г) электронные волны
Мы уже видели, что для фотона существует связь между волновыми
и корпускулярными свойствами уже в выражении для его энергии:
E = hν,
(10)
ν – это частота, связанная с волновым движением, а Е – энергия,
которая может быть выражена через корпускулярные характеристики,
такие как масса и скорость.
По уравнению Эйнштейна
Е = mc2,
(11)
где с – скорость света.
Приравнивая уравнения (10) и (11), получим:
hν = mc2.
(12)
Переходя к длине волны света
ν = c/λ,
(13)
получим
h/λ = mc λ = h/mc.
(14)
Отсюда, переходя к частице с массой m и скоростью v, получим:
λ = h/mv.
(15)
Длину волны такой частицы часто называют длиной волны де
Бройля. Исходя из формулы де Бройля, можно определить длину волны
любой материальной частицы, необходимо только знать ее кинетиче163
скую энергию и скорость. Кинетическую энергию определяют экспериментально:
E=
mv 2
2
Е для электрона на К-уровне или на первой орбите атома водорода
равна 0.218 ⋅ 10-10 эрг, или 0.218 ⋅ 10-17 Дж. Отсюда:
V=
λ=
2E
;
m
h
=
2mE
6,62 ⋅ 10 −27
2 ⋅ 9,1 ⋅ 10− 28 ⋅ 0,218 ⋅ 10 −10
= 3,33 Å.
Таким образом, длина волны электрона на первой орбитали атома
водорода равна 3,33 Å, r = 0,53 Å. Длина окружности l = 2πr, отсюда для
наружной орбиты l = 3.33 Å. Следовательно, длина волны электрона
совпадает с окружностью орбиты. Отсюда вывод: на стационарных орбитах, допускаемых квантовой механикой, длина волны электрона укладывается целое число раз, что подтвердило предположение де Бройля.
Если рассчитать длину волны для макрочастиц, например частицы
массой 1 г, движущейся со скоростью 1 см/с, то получим λ = 6.6 ⋅ 10-27
см. Это означает, что волновые свойства макрочастиц практически не
проявляются.
Предположение де Бройля было подтверждено экспериментально.
В 1927 г. американские физики Девиссон и Джермер, а также Томсон
(Англия) и П.С. Тартаковский (СССР) наблюдали дифракцию электронов на кристаллах металлов (кристалл никеля). В 1929 г. Штерн обнаружил сходную дифракцию при прохождении через вещество атомных и
молекулярных пучков.
Принцип неопределенности
В волновых свойствах электрона заложен первый принцип волновой механики. Вторым принципом является принцип неопределенности
Гейзенберга (1925 – 1927 гг.).
Согласно этому принципу невозможно точно определить местоположение частицы и ее импульс.
Чем точнее определяется координата частицы, тем более неопределенным становится ее импульс, и, наоборот, чем точнее известен импульс, тем неопределеннее координата.
164
Если мы утверждаем, что определенный объект – частица, то мы
должны уметь измерить корпускулярные свойства этого объекта (например, скорость и положение в пространстве). Это было бы нетрудно
сделать, если бы объектом служил мяч, но для электрона измерение этих
величин требует особого подхода.
Допустим, что у нас есть какой-то микроскоп, позволяющий увидеть движущийся электрон. Сначала электрон движется прямо. Однако
как только он столкнется с фотоном, имеющим сравнимую массу, то
изменятся направление движения и скорость движения электрона. Поэтому, наблюдая через малые промежутки времени, можно заметить, что
электрон движется зигзагообразно под влиянием ударов фотонов.
Для уменьшения влияния столкновения можно уменьшить энергию
фотонов. Но это приведет к увеличению длины волны света Е = ћν, λ =
c/ν, что уменьшит разрешающую способность микроскопа (т.е. точность, с которой можно определить положение электрона), зависящую
от длины волны излучения.
Таким образом, используя свет большой длины, мы точно узнаем
скорость электрона, но его положение точно определить не можем. С
другой стороны, свет с короткой длиной волны, состоящий из фотонов
высокой энергии (E = ћν), позволяет точно определить положение электрона, но его скорость определить нельзя, так как на скорость электрона
будут сильно влиять столкновения с фотонами.
Таким образом, чем точнее определяем мы положение электрона в
пространстве, тем неопределеннее его скорость, и наоборот, чем точнее
определяем мы скорость электрона, тем более неопределеннее положение электрона. Мы не можем одновременно точно определить положение частицы и ее скорость.
Соотношение неопределенностей имеет вид:
∆Χ ⋅ ∆V ≥
"
m!
"=
h
, (16)
2π
где ∆x – неопределенность положения частицы; ∆v – неопределенность
скорости. Таким образом записывается принцип Гейзенберга (1927).
Принцип неопределенности делает невозможным утверждение, что
электрон, имеющий определенную скорость, находится в том или ином
месте пространства. Мы можем только говорить о вероятности нахождения электрона в том или ином месте пространства.
165
Пример: Для электрона, движущегося по орбите со скоростью 1056
м/с, рассчитайте импульс и неопределенность по импульсу.
Решение: Допустим, что мы можем измерить положение электрона
с точностью до 0,01 Å, что составляет примерно 1% от типичного размера атома. Тогда
Р = mv = 10-30 кг 106 м/с = 10-24 кгм/с.
Согласно принципу неопределенности Гейзенберга неопределенность определения импульса составит:
h
0,5 ⋅ 10− 34
P = 2π =
= 0,5 ⋅ 10− 22 кгм/с
0,01 ⋅ 10−10
X
Отсюда видно, что неопределенность по импульсу в 50 раз больше
самого импульса.
Уравнение Шредингера
В 1925-1926 гг. Гейзенберг и Шредингер независимо друг от другa
предложили два варианта новой механики. Оба варианта приводят к
аналогичным результатам, но метод Шредингера оказался более удобным для выполнения расчетов, и поэтому современная теория строения
атомов и молекул основывается на этом методе. Механика микрообъектов получила название квантовой механики, в отличие от классической
механики, применяемой к макрообъектам.
Законы движения частиц в квантовой механике выражаются уравнением Шредингера:
−
h2  d 2Ψ d 2Ψ d 2Ψ 
⋅
+
+ 2  + UΨ = EΨ ,
8π 2 m  dx 2
dy 2
dz 
(17)
где h – постоянная Планка, m – масса частицы, U – потенциальная энергия частицы, E – полная энергия, x,y,z – координаты частицы.
Уравнение Шредингера описывает общие законы движения микрочастицы и является одним из постулатов квантовой механики. Справедливость этого уравнения подтверждается согласием с опытом. Уравнение Шредингера играет в квантовой механике ту же роль, что и законы
Ньютона в классической механике. Как и законы Ньютона, это уравнение невозможно вывести из каких-либо общих положений. Оно может
166
быть получено, исходя из определенной аналогии между уравнениями
механики и оптики. Его можно получить, если в дифференциальное
уравнение волны подставить λ из уравнения де Бройля и выразить импульс частицы через разность полной и потенциальной энергий.
Познакомимся с математическим описанием волнового движения.
Рассмотрим плоскую (одномерную) волну, которая с течением времени
передвигается по оси Х (рис. 4.3.):
Х
Х
Рис. 4.3. Плоская одномерная волна
Это волновое движение можно выразить уравнением:
d 2Α 1 d 2Α
= ⋅
,
dx 2 c dt 2
(18)
где А – амплитуда волны; с – скорость движения волны; t – время.
Решая это уравнение для одномерной волны, можно определить
амплитуду А во время t и в положении x:
 2πx 
Α = 2a sin 
 ⋅ cos 2πyt ,
 λ 
(19)
d 2 Ψ d 2 Ψ d 2 Ψ 4π 2
+
+ 2 + 2 Ψ = 0,
λ
dx 2
dy 2
dz
(20)
где а – константа; λ – длина волны.
Для трехмерного пространства дифференциальное уравнение имеет
вид:
где Ψ – это трехмерный аналог А. Это уравнение Шредингер выбрал как
основу для описания строения атома, так как, согласно гипотезе де
Бройля, электрон – это стоячая волна.
Поэтому, подставляя в волновое уравнение для трехмерной волны
длину волны де Бройля, получим:
167
d 2 Ψ d 2 Ψ d 2 Ψ 4π 2 m 2v 2
+
+ 2 +
= 0,
dx 2
dy 2
dz
h2
(21)
Учитывая, что полная энергия электрона в атоме является суммой
потенциальной U и кинетической mv2/2 энергий
mv 2
E=
+U ,
2
(22)
можно исключить v2 из уравнения волны и получить:
d 2Ψ d 2Ψ d 2Ψ
+
+ 2 + (E − U )Ψ = 0
dx 2
dy 2
dz
(23)
или
d 2 Ψ d 2 Ψ d 2 Ψ 2m
+
+ 2 + 2 (E − U )Ψ = 0 .
dx 2
dy 2
dz
h
(24)
Это уравнение и называется уравнением Шредингера. Часто оно записывается в следующем виде:
−
h2  d 2Ψ d 2Ψ d 2Ψ 
+
+ 2  + UΨ = EΨ ,
2m  dx 2
dy 2
dz 
(25)
где h – постоянная Планка; m – масса частицы; U – потенциальная энергия; E – полная энергия; x,y,z – координаты частицы.
Это уравнение можно записать и по-другому:
h2 2
V Ψ + UΨ = EΨ ,
2m
d 2Ψ d 2Ψ d 2Ψ
2
+
+ 2 – оператор Лапласа.
где ∇ =
dx 2
dy 2
dz
−
(26)
Очень часто уравнение Шредингера изображают в краткой форме:
(27)
HΨ = EΨ ,
где H – оператор Гамильтона, или оператор полной энергии.
H =−
h2  d 2Ψ d 2Ψ d 2Ψ 
⋅
+
+
+ UΨ = EΨ ,
2m  dx 2
dy 2
dz 2 
(28)
или
Н = –h2/2m ∇2Ψ + UΨ.
168
(29)
Величина Ψ называется волновой функцией. Ее квадрат имеет определенный физический смысл: величина Ψ2dV пропорциональна вероятности нахождения электрона в элементарном объеме пространства с
координатами x, y, z.
Величину Ψ2 называют плотностью вероятности, или электронной
плотностью.
Волновая функция должна быть конечной, непрерывной и однозначной, а также обращаться в нуль там, где частица не может находиться.
Волновые функции, являющиеся решениями уравнения Шредингера, могут быть сложными функциями пространственных переменных и
времени. Они зависят от конкретного вида движения частицы. Квантово-механическая теория атома и молекулы сводится к нахождению
удовлетворяющих уравнению Шредингера волновых функций и значений энергии Е.
Рассмотрим решение уравнения Шредингера в потенциальном поле
ядра. Примером такой системы является атом водорода.
Решения уравнения Шредингера для атома водорода были получены в 1927 г. Эти решения приводят к понятию атомной орбитали, квантовых чисел и квантованию энергий, которые являются фундаментальными в современной теории строения атома.
Для простейшей электронной системы – атома водорода – решение
уравнения Шредингера в полярных координатах дает волновую функцию общего вида:
Ψ = N [R(r)][Θ(ϑ)Φ(ϕ)],
(30)
где N – постоянная нормировки, задается стопроцентной вероятностью
нахождения электрона где-либо в пространстве около ядра;
R(r) – радиальная часть волновой функции, возведенная в квадрат,
показывает вероятность нахождения электрона в радиальном направлении от ядра на расстоянии r;
Θ(ϑ)Φ(ϕ) или Ф(x/r, y/r, z/r) – угловая часть волновой функции –
определяет форму поверхностей, ограничивающих пространство, в котором вероятность нахождения электрона составляет не менее 90%.
Пространство, которое включает в себя 90% электронного облака,
называется орбиталью. Другими словами, орбиталь – это волновая
функция, описывающая состояние электрона. С ее помощью можно рассчитать распределение электронной плотности в заданном пространстве.
169
Волновые функции водородоподобного атома и атома водорода
имеют сложный вид и приведены в табл. 4.1 и 4.2.
Таблица 4.1
Некоторые волновые функции водородоподобного атома
n
l
m Обозначение
1
0
0
1s
2
0
0
2s
2
1
0
2pz
2
1
1
2px
2
1
-1
2py
3
0
0
3s
3
1
0
3pz
3
1
1
3px
3
1
-1
3py
3
2
0
3dz2
3
2
1
3dxz
170
Функции
(
π Z a0
1
1
)
3
2
e − zr a
(Z a 0 ) 2 (2 − zr
a 0 )e − zr 2a 0
(Z a 0 ) 2 re −zr a
cos Θ
3
4 2π
1
4 2π
1
5
(Z a )
2π
5
(Z a )
2π
5
1
4
re − zr 2a 0 sin Θ cos ϕ
2
re −Zr 2a 0 sin Θ cos ϕ
0
(Z a ) (27 − 18Z
3π
1
81
3
2
0
2
81 π
2
81 π
2
81 π
1
81
0
2
0
4
0
r
)
a 0 + 2Z 2 r 2 a 20 e −Zr 3a 0
(Z a 0 ) 2 (6 − Zr a 0 )re −Zr 3a
0
cos Θ
(Z a 0 ) 2 (6 − Zr a 0 )re −Zr 3a
0
sin Θ cos ϕ
(Z a 0 ) 2 (6 − Zr a 0 )re −Zr 3a
0
sin Θ cos ϕ
5
5
5
(Z a )
6π
0
7
2
r 2e −Zr 3a 0 (3 cos2 Θ − 1)
(Z a )
6π
7
(Z a )
6π
7
(Z a )
6π
7
(Z a )
6π
7
1
3
2
-1
3dyz
2
81
1
2
3
2
2
3dx –y
3
2
-2
3dxy
81
2
r 2e −Zr 3a 0 sin Θ3 cos Θ sin ϕ
2
r 2e −Zr 3a 0 sin 2 Θ3 cos 2ϕ
2
r 2e −Zr 3a 0 sin 2 Θ3 cos 2ϕ
0
1
81
r 2e −Zr 3a 0 sin Θ cos2 Θ sin ϕ
0
1
81
2
0
0
Таблица 4.2
Некоторые волновые функции электрона в атоме водорода
Орбиталь
Радиальная часть
12 π
1s
2s
2px
2py
2pz
3d x2 − y2
3dxz
3dz2
3dyz
Угловая часть
− 1 2 π (2 − r )e
1
2 6
1
2 6
1
2 6
re − r 2
re − r 2
re − r 2
4
81 30
4
81 30
4
81 30
4
81 30
r 2e −r 3
r 2e −r 3
r 2e −r 3
r 2e −r 3
−r 2
12 π
3
2 π
3
2 π
3
2 π
15
4 π
(x r )
(y r )
(z r )
[(x
30
5
)r]
− y2
2
(xz r )
2
2 2π
4 π
2
[(3z − r ) r ]
30
2 2π
2
2
2
(yz r )
2
3dxz
171
4
81 30
r 2e −r 3
Почему мы говорим об электронном облаке, а не об электроне?
Электрон наряду с корпускулярными свойствами проявляет и волновые
свойства, поэтому его состояние нельзя представить как движение материальной частицы по какой-либо орбите. Квантовая механика рассматривает вероятность пребывания электрона в пространстве вокруг ядра. В
качестве квантово-механической модели электрона в атоме принято
представление об электронном облаке, плотность соответствующих участков которого пропорциональна вероятности нахождения там электрона. Чем прочнее электрон связан с ядром, тем меньше должно быть
электронное облако по размерам и более плотным по распределению
заряда.
Существуя в трехмерном пространстве, электрон имеет три степени
свободы, а это приводит к тому, что в решении уравнения Шредингера
появляются три величины, которые могут принимать только целочисленные значения – три квантовых числа, которые обозначаются буквами
n, l, m. Тогда результат решения уравнения Шредингера для атома водорода можно выразить так:
R(r) = f1(n,l); Θ(ϑ) = f2(l,ml); Ф(ϕ) = f3(m).
Квантовые числа n, l, m могут принимать следующие значения:
n = 1, 2, 3, 4,...n
m = 0, ±1, ±2, ±3...±4...
l = 0, 1, 2, 3...(n-1)
Рассмотрим возможные значения квантовых чисел n, l и m.
n = 1, l = 0 1s – орбиталь, ml = 0
172
Рис. 4.4. Вид s-орбитали
S-орбитали характеризуются l = 0 и m = 0, т.е. всего одним значением магнитного квантового числа, определяющего ориентацию подуровня в пространстве. Такие орбитали являются безразличными к ориентации, имеют максимально симметричную форму – сферическую.
Рис. 4.5. Распределение электронной плотности s-орбиталей в зависимости от
значения главного квантового числа
Если начертить кривые распределения вероятности нахождения
электрона для подуровней с l = 0 (т.е. s) для слоев n = 1, n = 2, n = 3 и
т.д., то они будут иметь вид, приведенный на рисунке 4.5. Из рис. 4.5
видно, что с удалением слоя от ядра (с увеличением r) вероятности становятся все более размытыми и образуют несколько концентрических
орбиталей: для 1s – одну, для 2s – две, для 3s – три, между которыми Ψ2
= 0.
n=2
l=0
2s – орбиталь
l=1
2p – орбиталь, ml = -1, 0, +1.
Р-орбитали существуют при n ≥ 2 и l = 1 и ориентированы в пространстве по трем направлениям рx, рy, рz (рис. 4.6)
173
Рис. 4.6. Пространственная ориентация p-орбиталей
Электроны, находящиеся на любой из трех р-орбиталей, обладают в
изолированном атоме одинаковой энергией. Такое состояние называется
вырожденным. Поэтому рx, рy, рz-орбитали являются трижды вырожденными, так как они неразличимы по энергии (в изолированном атоме).
При приложении магнитного или электронного поля вырождение снимается.
n=3
l=0
3s-орбитали
m=0
l=1
3p-орбитали
m = -1, 0, +1
l=2
3d-орбитали
m = -2, -1, 0, +1, +2.
d-орбитали характеризуются пятью способами ориентации в пространстве. Каждая из них изображается в виде "четырехлепестковой
розы". d-орбитали ориентированы либо между осями координат 3dxy,
3dxz, 3dyz, либо вдоль осей координат 3dz2, 3dx2 – y2. В изолированном
атоме d-орбитали пятикратно вырождены, т. е. все пять атомных dорбиталей имеют одинаковую энергию (рис. 4.7).
174
Рис. 4.7. Пространственная ориентация d-орбиталей
n=4
l=0
l=1
l=2
l=3
4s-орбитали,
4p-орбитали,
4d-орбитали,
4f-орбитали,
m=0
m = -1,0,+1
m = -2,-1,0,+1,+2
m = -3,-2,-1,0,+1,+2,+3.
4f-орбитали изображаются в виде восьмилепестковых фигур и
имеют три узловых плоскости.
Часто электронным уровням, соответствующим главным квантовым числам, присваивают определенные буквенные обозначения:
n=1
K-уровень;
n=2
L-уровень;
n=3
M-уровень;
n=4
N-уровень;
n=5
P-уровень.
Квантовые числа характеризуют движение электронов не только в
атомах водорода, но и в любых других атомах. Эти характеристики важны для понимания свойств веществ и природы химической связи. Поэтому рассмотрим их более подробно.
Квантовые числа n,l,m определяют геометрические особенности
электронного облака. Они также связаны с физическими характеристиками движения электрона.
Квантовое число n – это главное квантовое число. Оно определяет
энергию электрона. Квантовое число n равно числу узловых поверхностей орбиталей.
175
Узловой поверхностью орбитали называется геометрическое место
точек, для которых Ψ = 0. Так как Ψ = 0, то и Ψ2 = 0. Таким образом, на
узловой поверхности плотность электронного облака равна нулю. В
число узловых поверхностей включается также поверхность, лежащая
на бесконечном удалении от ядра.
Существование узловых поверхностей в распределении электронной плотности связано с общими закономерностями микромира. Движение микрочастиц описывается соотношениями, аналогичными уравнениям волновой механики. В любой волне имеются точки, где смещение
колеблющейся величины равно нулю. Если колебательный процесс происходит в трех измерениях, то совокупности данных точек образуют
узловую поверхность.
Рис. 4.8. Вид узловых поверхностей орбиталей
Узловые поверхности бывают двух типов: не проходящие через
центр атома (ядро) и проходящие через него.
Первые являются сферами, центр которых совпадает с ядром, вторые являются плоскими или коническими поверхностями.
Рис. 4.9. Вид узловых поверхностей орбиталей, не проходящих через центр атома (а) и проходящих через центр атома (б)
176
Наличие сферических узловых поверхностей проявляется в радиальной части волновой функции – на определенных расстояниях от ядра
Ψ бывает равна нулю.
Величина l показывает, сколько узловых поверхностей волновой
функции электрона проходит через ядро. Мы уже знаем, что одна из
узловых поверхностей всегда лежит на бесконечно большом удалении
от ядра. Отсюда понятно, почему l изменяется от 0 до (n-1). Квантовое
число l определяет симметрию орбитали.
Все s-орбитали (l = 0) сферические. p-орбитали (l = 1) имеют форму
гантели; d-орбитали (l = 2) – четырехлепестковой розы и т.д.
Квантовое число l часто называют орбитальным; оно определяет
величину орбитального момента импульса электрона
М = ћ √l(l+1)
ћ = h/2π.
Электрон, в соответствии с представлениями квантовой механики,
может находиться на любом расстоянии от ядра, но вероятность его
пребывания в разных местах атома различна.
Зная распределение электронной плотности, можно вычислить
среднее расстояние электрона от ядра rср, которое характеризует размер
орбитали (орбитальный радиус). Величина rср определяется значениями
n и l. Так, для электрона в атоме водорода
rср = (a0n2)/z{1 +0.5[1 – (l(l + 1))/n2]},
где z – заряд ядра; rср пропорционально n2, т.е. значения n определяют
размер орбиталей электрона; а0 = rср = 0.53 °А – т.е. максимальная плотность 1s-электрона совпадает с радиусом соответствующей боровской
орбиты.
Квантовое число ml характеризует расположение орбитали в пространстве. Его еще называют магнитным, так как оно определяет проекции орбитального магнитного момента электрона на ось атома. Магнитное квантовое число характеризует ориентацию электронных облаков по
отношению к магнитной оси атома.
Электрон, как и всякий электрический заряд, движется по замкнутому контуру, имеет собственный магнитный момент. Величина проекции этого момента на одну любую ось координат во внешнем магнитном поле принимает определенные квантовые значения, которые и
характеризуют расположение подуровня в пространстве. Каждый поду-
177
ровень в уровне имеет столько значений ориентации, сколько значений
имеет m. Для каждого подуровня ml = 2l +1, от l = -1 до l = +1. Так, для
l=0
l=1
l=2
l=3
m = 0, т.е. одно значение,
m = -1,0,+1, т.е. три значения,
m = -2,-1,0,+1,+2 пять значений,
m = -3,-2,-1,0,+1,+2,+3 семь значений.
Таким образом, каждый подуровень состоит из ориентированных в пространстве областей, в которых наиболее вероятно нахождение электрона
(атомные орбитали – АО). Графически атомные орбитали обозначают
или
.
Кроме квантовых чисел n, l, m, известно еще одно. Это так называемый спин (S) электрона. Упрощенно он показывает вращение электрона вокруг собственной оси.
Тонкие исследования показали, что электрон обладает не только
электростатическим полем, но и магнитными свойствами. Если пропустить пучок электронов через сильно изменяющееся магнитное поле, то
он распадается на два пучка. Степень отклонения свидетельствует о том,
что каждый электрон ведет себя как маленький магнитик, который ориентирован по полю либо параллельно, либо в строго противоположном
направлении (антипараллельно). Магнитное состояние квантуется, и
существуют только два возможных состояния. В микромире магнитное
поле возникает при движении электрического заряда по кривой траектории. Предполагается, что в электроне заряд каким-то образом вращается, т.е. говорят, что электрон имеет спин. Это предположение позволяет
вычислить магнитное поле, создаваемое спином. Но полученный результат оказывается вдвое больше экспериментальной величины. Почему?
При вращении электрона угловой момент определяется распределением массы, а магнитное поле – распределением заряда. Если распределение заряда и масса не идентичны друг другу, то классические вычисления дадут неверное соотношение между угловым моментом и
магнитным полем. А это наблюдается и на самом деле.
S = ±1/2. Величина 1/2 представляет собой коэффициент расхождения между экспериментом и простым расчетом для отношения момента
к полю.
Многоэлектронные атомы
178
Точное решение уравнения Шредингера возможно только для атома водорода. Поведение электрона в многоэлектронных атомах осложняется межэлектронным взаимодействием, что значительно затрудняет
нахождение волновых функций. Для многоэлектронных атомов приходится пользоваться приближенными решениями и схемами. Для решения уравнения Шредингера для многоэлектронных атомов используется
метод самосогласованного поля, разработанный Д. Хартри и В. Фока. В
этом методе каждый электрон рассматривается движущимся в поле,
создаваемом ядром атома и остальными электронами. Это позволяет
заменить член уравнения Шредингера, учитывающий межэлектронное
взаимодействие и зависящий от координат всех электронов, выражением, описывающим межэлектронное взаимодействие как функцию координат каждого отдельного электрона. Тогда полная волновая функция
атома запишется в виде произведения волновых функций отдельных
электронов:
Ψ = Ψ1(1) Ψ2(2) Ψ3(3) ....Ψn(n).
(31)
Тем не менее, поскольку характер движения электрона в многоэлектронных атомах определяется размером электронного облака, орбитальным, магнитным и спиновым моментами электрона, оказалось возможным квантовые состояния электрона в атоме водорода перенести на
многоэлектронные атомы. (Однако это справедливо только для легких
элементов. Начиная с цинка, вследствие высокого заряда ядра и межэлектронного взаимодействия атомы нельзя считать водородоподобными). Химические свойства элементов определяются электронным строением. Поэтому установление электронной структуры атомов
необходимо для предсказания химических свойств элементов.
Состояние электронов в атоме определяется значениями четырех
квантовых чисел n, l, m, s. Для построения электронных структур многоэлектронных атомов следует исходить из того, что в атоме будут заполняться все орбитали в порядке увеличения энергии электрона на каждой из них. Одним из принципов, определяющих порядок заполнения
электронов в атоме, является принцип Паули (или принцип исключения). Он формулируется так: в атоме не может быть двух электронов
с четырьмя одинаковыми значениями квантовых чисел. Иными словами, данными значениями квантовых чисел n, l, m, s может характеризоваться только один электрон. Для любого другого электрона в атоме
должно быть иным хотя бы одно из квантовых чисел.
179
Из принципа Паули также вытекает, что на орбитали может находиться лишь два электрона с S = – 1/2 или S = + 1/2.
Отсюда в s-состоянии находятся два электрона, в p-состоянии – 6, в
d-состоянии – 10, а в f – 14 электронов.
Поскольку каждый энергетический уровень включает n2 орбиталей,
его емкость равна 2n2. Отсюда по мере удаления от ядра емкость уровня
увеличивается и составляет 2 (n = 1), 8 (n = 2), 18 (n = 3), 32 (n = 4).
Таким образом, принцип Паули дает возможность рассчитать емкость электронных уровней и подуровней.
Если n = 1, то l = 0 и m = 0, в этом случае электроны могут различаться только спинами. Так как для n = 1 возможно только одно значение орбитального квантового числа l = 0, то оба электрона первого слоя
будут s-электронами. Они находятся на s-орбитали шаровой симметрии.
Водород имеет 1s1 – электрон, гелий – 2s2. Таким образом, в гелии первый электронный слой заполнен полностью и содержит два электрона.
При n = 2 l = 0, 1, т.е. принимает два значения, и электрон-ный
слой распадается на два подуровня.
При l = 0 m = 0, и на этом подуровне могут быть только два электрона Li 1s22s1, Be 1s22s2 ⋅ 2s – это первый подуровень второго электронного слоя. Второй подуровень l = 1 и m = -1, 0, +1, т.е. может содержать
еще шесть электронов. Этот подуровень называется 2р-подуровнем, а
соответствующие ему электроны называются 2р-электронами.
В 1s22s22p1
↑↓, ↑↓, ↑  .
1s 2s 2p
Следующий элемент – углерод. Его второй р-электрон может пойти
на свободную р-орбиталь или идти на спаривание на занятой орбитали.
Квантово-механические расчёты показали, что предпочтительнее расположение электрона на вакантной орбитали. В этом случае энергия системы ниже. Констатацией этого факта является правило Хунда, определяющее порядок заполнения орбиталей электронами:
В пределах подуровня электроны заполняют максимальное
число орбиталей.
С 1s22s22p2
↑↓, ↑↓, ↑ ↑  .
1s 2s 2p
В соответствии с правилом Хунда второй р-электрон в атоме углерода займет пустую орбиталь, а не ту, на которой уже есть электрон.
180
В атоме азота все р-орбитали оказываются занятыми по одному
электрону
N 1s22s22p3
↑↓, ↑↓, ↑ ↑ ↑,
1s 2s 2p
и восьмой электрон атома кислорода помещается на занятую рорбиталь, образуя пару электронов с антипараллельными спинами:
О 1s22s22p4
↑↓, ↑↓, ↑↓ ↑ ↑
1s 2s
2p
У фтора и неона расположение электронов в атоме следующее:
Ne ↑↓, ↑↓, ↑↓ ↑↓ ↑↓
F ↑↓, ↑↓, ↑↓ ↑↓ ↑
1s 2s
2p
1s 2s
2p
Если атом имеет несколько одиночных электронов, то спиновые
моменты суммируются. Поэтому спины атомов равны: бора 1/2; углерода 1; азота 3/2; кислорода 1; фтора 1/2; неона 0. С учетом этого правило
Хунда формулируется так: Суммарный спин электронов в данном
подуровне должен быть максимальным.
У элементов, следующих за неоном, должно идти заполнение слоя с
n = 3, так как на слое n = 2 уже нет свободных орбиталей и подуровней.
Слой с n = 3 состоит из 3s, 3p, 3d-подуровней. У атомов Na и Mg
заполняется 3s-подуровень:
Na 1s22s22p63s1
Mg 1s22s22p63s2.
Затем у шести последующих за ними элементов от Al до Ar идет заполнение 3р-подуровня:
Al 1s22s22p63s23p1
..................................................................
Ar 1s22s22p63s23p6.
Далее должно бы идти заполнение 3d-подуровня, но на самом деле
идет сначала заполнение 4s-подуровня, а только затем идет заполнение
3d-подуровня. Дело в том, что 4s-подуровень по энергии лежит ниже,
чем 3d-подуровень. Сферическая орбиталь значительно меньше испытывает отталкивание от нижележащего уровня с n = 2, чем d-орбитали.
181
Это приводит к тому, что за за аргоном идет заполнение 4s-электронов у
атомов К и Са.
Ca 1s22s22p63s23p64s2.
K 1s22s22p63s23p64s1
И только после Са идет заполнение 3d-подуровня у скандия и далее
у десяти элементов, следующих за ним до Zn.
Sc 1s22s22p63s23p63d14s2
В многоэлектронных атомах электрон движется не только в поле
ядра, но и в поле других электронов. Это приводит к тому, что энергия
электронов, обладающих одинаковыми n, но различными l, становится
различной вследствие экранирования положительного заряда ядра электронами нижележащих электронных слоев и проникновения электронов
внешнего слоя через внутренние слои к ядру (рис. 4.10).
182
-E
0,1
7p 5d 7d
7s
6s
5s
4s
3s
4p
3d
2s
2p
6g
6f
7d
3s
6d
7p
7s
5f
2s
1,0
1s
6p
6s
5d
5p
5s
4f
4d
4p
4s
3d
3p
3s
s
p
10
d
f
g
2p
2s
1s
100
1
H
10
H e
Li Be
N Ne
Ca
100
ZnZr N dH g
Рис. 4.10. Расположение энергетических уровней в многоэлектронных атомах
Наиболее сильно проникают к ядру s-электроны, затем рэлектроны, затем d-электроны. Поэтому s-электроны более прочно связаны с ядром. Отсюда энергия электронов в многоэлектронных атомах
определяется значениями двух квантовых чисел: n и l. При этом энергия
возрастает как с увеличением n, так и с увеличением l. Зависимость
энергии от l становится тем более заметной по сравнению с зависимостью от n, чем больше электронов содержит атом. Так, для наиболее
удаленного от ядра электрона в атоме натрия разность энергий для
уровней n = 3, l = 0 (3s) и n = 3, l = 1 (3p) равна 2.1 эВ. Эта величина
приближается к разности энергий уровней с n = 3, l = 0 (3s) и n = 4, l = 0
(4s), равной 3.1 эВ.
183
Для более многоэлектронных атомов влияние l на энергию электрона в некоторых случаях оказывается более значительным, чем влияние
n. А это приводит к некоторым особенностям строения атомов. Правило
заполнения орбиталей многоэлектронных атомов было сформулировано
Клечковским:
Заполнение орбиталей происходит в последовательном увеличении суммы главного и орбитального квантовых чисел (n+l). При
каждом значении суммы n + l заполнение идет от больших l и
меньших n к меньшим l и большим n.
Таблица 4.3
Значения квантовых чисел n + l и порядок заполнения атомных орбиталей
n+1
n
l
Электронное
состояние
1
2
3
3
4
4
5
5
5
6
6
6
7
7
7
7
1
2
2
3
3
4
3
4
5
4
5
6
4
5
6
7
0
0
1
0
1
0
2
1
0
2
1
0
3
2
1
0
1s
2
2p
3s
3p
4s
3d
4p
5s
4d
5p
6s
4f
5d
6p
7s
В общем случае порядок заполнения энергетических уровней примерно следующий (табл. 4.3):
1s<2s<3p<3s<3p<4s≈3d<4p<5s≈04d<5p<6s≈5d≈4f<6p.
Из этого ряда видно, что аномалии в порядке заполнения имеются и
для 4d-электронов, и для 4f-электронов, а также для 5d- и 5f-электронов.
Появление 4s-электронов при наличии незаполненного 3dподуровня обусловливается экранированием ядра плотным слоем 3s23p6184
электронов. В связи с этим происходит отталкивание от этого слоя для
19-го 3d-электрона, так для К и Са оказывается энергетически более выгодным 4s-состояние.
При последующем возрастании эффективного заряда ядра у следующего за Са элемента Sc 3d-состояние становится энергетически более выгодным, чем 4р-состояние, и у последующих за Sc элементов
происходит заполнение предвнешнего 3d-подуровня, после завершения
которого заполняется 4р-подуровень у элементов Ca – Kr. Таким образом, четвертый период начинается s-элементами и заканчивается 4рэлементами. В пятом периоде заполнение идет аналогично. Шестой период содержит 32 элемента и также начинается двумя s-элементами: Cs
и Ba. Далее у La начинается заполнение 5d-подуровня предвнешнего
слоя.
La
1s22s22p63s23p63d14s24p64d15s25p65d16s2.
У следующих за лантаном четырнадцати элементов (Ce – Lu)
вследствие роста эффективного заряда происходит заполнение 4fподуровня:
Ce 1s22s22p63s23p63d14s24p64d14f25s25p66s2
..........................................
Lu 1s22s22p63s23p63d104s24p64d104f145s25p65d16s2.
Затем продолжается заполнение 5d-подуровня, и период заканчивается шестью р-элементами (Tl – Rn).
Седьмой период заполняется аналогично.
Из вышеизложенного видно, что конфигурация электронной оболочки атома однозначно определяется зарядом ядра. По мере роста заряда ядра происходит закономерная периодическая повторяемость
сходных электронных структур, а отсюда и повторяемость свойств элементов.
Термы многоэлектронных атомов
Для объяснения химических свойств атомов необходимо знать распределение электронов в пределах подуровня. Если электронная оболочка полностью заполнена (замкнутая оболочка), то для неё существует
единственный способ распределения электронов по орбиталям. Например для атома неона
185
Ne 1s22s22p6 ↑↓, ↑↓, ↑↓ ↑↓ ↑↓
1s 2s
2p
В случае незаполненной (не замкнутой) оболочки существует несколько вариантов расположения электронов на подуровне. Так, для
атома углерода это относится к двум электронам на 2р-подуровне, в
атоме хрома – к пяти электронам на 3d-подуровне и одному электрону
на 4s-подуровне. В атоме марганца – к пяти электронам на 3d-подуровне
и т.д. Часть этих электронных конфигураций может иметь одинаковую
энергию, образуя набор вырожденных состояний. Конфигурация с наименьшей энергией относится к основному состоянию, остальные конфигурации являются возбуждёнными. Энергии каждой электронной конфигурации можно вычислить с помощью методов квантовой механики.
Несмотря на большую трудоёмкость такие расчёты были сделаны для
всех элементов периодической системы и даже для ещё не синтезированных элементов. Анализ таких расчётов позволяет перейти к другой
формулировке квантовых чисел.
Рассмотрим варианты расположения электронов на 2р-подуровне
атома углерода:
l = 1 0 –1
l = 1 0 –1
l = 1 0 –1
а) ↑↓,  
б),  ↑↓ 
в),   ↑↓
г) ↑ ↑ 
д) ↑ ↓ 
е) ↓ ↓ 
з) ↑  ↓
и) ↓  ↓
ж) ↑  ↑
к)  ↑ ↑
л)  ↑ ↓
м)  ↓ ↓
н) ↓  ↑
o)  ↓ ↑
п) ↓ ↑ 
Таким образом, для атома углерода расположение электронов на
2р-подуровне может характеризоваться 15 вариантами. Для выбора наиболее оптимального варианта необходимо найти значения полных орбитального и спинового квантовых чисел L и S.
Дело в том, что в многоэлектронных атомах квантовые числа l1 отдельных электронов теряют своё значение, так как каждый электрон
испытывает межэлектронное взаимодействие и движется не в сферически симметричном поле, в отличие от атома водорода. Из этого следует,
что вследствие принципа неразличимости им уже не могут быть приписаны собственные угловые и спиновые моменты. Физический смысл
имеют лишь полные орбитальный и спиновый моменты совокупности
электронов.
186
Полное орбитальное квантовое число L определяют через значения
орбитальных квантовых чисел l1 отдельных электронов. L может принимать только положительные целочисленные значения и значение, равное
нулю. Заполненные оболочки s2, p6,d10, f14 имеют полный момент, равный нулю. Для вычисления L различных электронных систем необходимо рассматривать только незаполненные оболочки. Для двух электронов
с орбитальными квантовыми числами l1 и l2 квантовое число L принимает значения:
L = (l1 + l2), (l1 + l2 – 1), ....(l1 – l2 + 1), l1 – l2.
Если имеется три электрона с li ≠ 0, то сложение моментов может
быть произведено путём последовательного сложения вначале li для
двух электронов, а затем сложения каждого полученного значения L с l3.
Например, для двух р-электронов углерода с l1 = l2 = 1L принимает значения 2,1,0. Для двух p- и d-электронов с l1 = 1 и l2 = 2 L = 3,2,1.
Так же, как и в атоме водорода, состояния с различными значениями L имеют буквенные обозначения:
L .......0 1 2 3 4 5
Обозначение ......S P D F G H
Полное спиновое квантовое число S находится по аналогичным
правилам. Для заполненных оболочек S = 0. Квантовое число S может
принимать следующие значения:
S = N/2, N/2 – 1, N/2 -2, ,,,,1/2 (или 0),
где N – число электронов в незаполненной оболочке.
В зависимости от числа электронов на незаполненной оболочке
атома (чётное или нечётное) квантовое число S может быть целым или
полуцелым.
Так же как для проекций орбитального l и спинового mS моментов
электрона в атоме водорода, в многоэлектронных атомах вводятся проекции полного орбитального и полного спинового моментов, принимающие дискретные значения:
ML = L, L – 1, L – 2.....–L + 1, –L, всего 2L + 1 значение;
MS = S, S – 1, ......–S + 1, –S, всего 2S + 1 значение.
187
Полные орбитальный и спиновый моменты количества движения
электрона в атоме не являются независимыми друг от друга, так как сопряжены с собственным магнитным моментом. Взаимодействие магнитных полей, создаваемых этими моментами, называется спинорбитальным взаимодействием. Это взаимодействие обусловливает дополнительное расщепление атомных спектров. Оно позволяет объяснить
тонкую структуру атомных спектров. Для учёта этого взаимодействия
вводят величину полного углового момента атома J, являющегося векторной суммой полного орбитального и спинового моментов:
J = L + S.
Полный угловой момент атома квантуется и принимает целые или полуцелые значения и равен
J = L + S,
L + S – 1,....L – S + 1,
L – S.
Вернёмся к атому углерода. По вариантам расположения электронов на 2р-подуровне проведём подсчёт L и S.
Для варианта а:
L = l1 + l2 = 1 + 1 = +2, S = +1/2 – 1/2 = 0
Для варианта б:
L = 0 + 0 = 0,
S = +1/2 – 1/2 = 0.
Для варианта в:
L = (-1) + (-1) = -2,
S = 1/2 – 1/2 = 0
и так далее. Результаты подсчёта L и S представим в виде табли- цы 4.4.
Из таблицы 4.4 видно, что в атоме углерода L принимает значения от +2
до –2 (варианты а и б), а S принимает значения от +1 до -1 (варианты г,
ж, к, е, и, м). Для решения вопроса о размещении электронов используют правило Хунда: в пределах подуровня полный спин должен быть
максимальным. Этому соответствует шесть состояний: г, к, ж, е, и, м.
При равенстве S из нескольких вариантов выбирают состояния с наибольшим L. Этому соответствуют состояния г, к, е, м. Для атома углерода это равноценные состояния.
Таблица 4.4
Значения S и L для двух электронов на 2р-орбиталях атома углерода
L
S
+2
188
+1
о
-1
-2
+1
-
г
ж
к
-
0
a
д,п
б,з,н
л,о
в
-1
-
е
и
м
-
Определённое энергетическое состояние атома называется
атомным термом. Классификация термов осуществляется в соответствии со значениями L, S, J. Терм обозначается 2S+1LJ.
2S + 1 – мультиплетность, определяемая величиной полного спина
S, показывает число возможных значений проекций полного спинового
момента. Мультиплетные состояния записываются следующим образом:
S=0
S = 1/2
S=1
S = 3/2
2S + 1 = 1 синглетное состояние;
2S + 1 = 2 дублетное состояние;
2S + 1 = 3 триплетное состояние;
2S + 1 = 4 квартетное состояние.
Как мы уже видели на примере атома углерода, для данной электронной конфигурации может существовать несколько термов. Их порядок расположения определяется правилами Хунда:
1. Терм основного состояния всегда имеет максимальное значение
спиновой мультиплетности.
2. Если несколько термов имеют одинаковую мультиплетность, то
наиболее стабилен тот, что имеет максимальное значение L.
3. Для конфигурации с меньше чем наполовину заполненной оболочкой наиболее стабилен терм с минимальным значением J. Если же
подуровень заполнен более чем наполовину, то самым стабильным будет терм с максимальным значением J.
Лучше всего правила Хунда подходят для определения терма основного состояния.
Для определения терма основного состояния удобно пользоваться
следующими правилами:
1. Записывается электронная конфигурация незаполненного подуровня.
2. Электроны на орбиталях располагают так, чтобы в соответствии
с первым и вторым правилами Хунда получить максимальные значения
L и S, т. е. составить конфигурацию с максимальным числом неспаренных электронов и максимально возможным числом электронов на орбиталях с наибольшим значением магнитного квантового числа m 4i 0.
189
L.
3. Квантовые числа li неспаренных электронов суммируются и дают
4. По числу неспаренных электронов определяют S и мультиплетность терма.
5. В соответствии с третьим правилом Хунда находится J.
Пример: Определить термы основного состояния атомов кислорода
и хрома.
Решение. Электронная конфигурация атома кислорода 2P4, графическая формула имеет вид:
↑↓ ↑ ↑
m = 1 0 –1
Отсюда L = 0 + 1 = 1 Р-состояние. S = 1/2 + 1/2 = 1, мультиплетность 2S + 1 = 3 триплетное состояние.
Возможные значения J = 2,1,0. Так как оболочка атома кислорода
заполнена больше чем наполовину, то выбирается J = 2. Таким образом,
терм основного состояния атома кислорода имеет вид 3Р2.
Для атома хрома электронная конфигурация имеет вид 3d54s1, графическая формула
3d
4s
↑ ↑ ↑ ↑ ↑, ↑
m = 2 1 0 -1 -2 0
L = 2 + 1 + 0 + (-1) + (-2) = 0 S-состояние
S = 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 = 3
Мультиплетность 2S + 1 = 7. J имеет только одно значение 3. Тогда
терм атома хрома записывается в виде 7S3.
Для атома углерода данные таблицы указывают на возможность
существования нескольких термов. Так, состоянию с L = 2, S = 0 соответствует терм 1D, которому удовлетворяет пять микросостояний. Для
набора с L = 1 и S = 1 соответствует терм 3Р, ему соответствует девять
состояний. Набору L = 0 и S = 0 соответствует терм 1S с одним соответствующим состоянием.
Правила Хунда позволяют определить устойчивость полученных
термов 3Р > 1D >1S. Терм 3P девятикратно вырожден (трижды по L и
190
трижды по S), терм 1D – пятикратно вырожден (по орбитальному числу),
а терм 1S – является невырожденным.
Для терма 3Р возможны три значения J = 2,1,0. Согласно третьему
правилу Хунда энергетическая устойчивость термов имеет следующий
порядок: 3P0 > 3P1 > 3P2. Основное состояние имеет терм 3P0. Термы 1D и
1
S имеют соответственно J = 2 и J = 1 и записываются в виде 1D2 и 1S0.
Термы конфигураций, содержащих n эквивалентных электронов
(имеющих одинаковые n и l), совпадают с термами конфигураций, для
которых не хватает n электронов до завершения оболочки. Так, термы
конфигураций p2 и p4, d1 и d9 одинаковы. Термы полностью заполненных оболочек всегда 1S.
Величины разностей энергий термов обычно сравнимы с энергиями
химических связей и химических реакций. Так, энергии 1D и 1S термов
атома углерода с электронной конфигурацией 1S22S22P2 выше терма
основного состояния 3Р на 105 и 235 кДж/моль соответственно.
Строение и классификация атомных ядер
Понятие об атомном ядре возникло в 1910 г. в результате работ,
проводимых под руководством знаменитого английского физика Резерфорда. Его сотрудники Гейгер и Марсден при изучении прохождения αлучей через пластины из различных металлов обнаружили удивительное
явление – отражение α-частиц от мишени. Для опытов они использовали
очень простой прибор, состоящий из стеклянного капилляра с запаянной
в нем "эманацией радия" – инертным газом радоном. Конец капилляра
был заклеен тонким слюдяным окошком, пропускавшим α-частицы (но
не пропускавшим радон). Альфа-частицы попадали на сцинтиллирующий экран, покрытый ZnS или K2PtCl6. Эти вещества под действием αчастиц дают вспышки, которые можно наблюдать через микроскоп.
Причиной вспышек (сцинтилляций) является деформация кристаллической решетки сцинтиллирующего вещества. Кристалл под действием
излучения как бы расширяется, а затем сжимается, поглощая энергию на
первой стадии и выделяя ее на второй. В опыте Гейгера и Марсдена между капилляром с радоном и сцинтиллирующим экраном помещались
пластинки различных металлов, которые испытывались на способность
поглощать α-лучи. Число α-частиц, попавших на экран, т.е. прошедших
через тот или иной поглотитель, фиксировалось визуально с помощью
микроскопа (по числу вспышек на экране). Опыт Гейгера и Марсдена
очень типичен для того времени. Аппаратура была очень простой, мож191
но ее назвать даже примитивной. Но ясная мысль исследователей позволяла простыми методами открывать новые факты и фундаментальные
закономерности, не прибегая к сложным в аппаратурном оформлении
экспериментам.
Однажды исследователи поместили сцинтиллирующий экран и
микроскоп не прямо за пластиной металла, а сбоку. С удивлением они
обнаружили вспышки на экране и в этом случае. При этом было установлено, что при прочих равных условиях алюминиевая пластинка давала 3 отражения α-частиц в минуту, железная – 10, медная – 15. Таким
образом, становилась ясной закономерность: чем больше атомная масса
элемента или, что более важно, чем больше атомный номер элемента,
тем большее число α-частиц отклоняется от прямолинейного пути. Листок серебра отклонил 27 α-частиц в минуту, олово – 34, платина – 63 и
т.д.
Поскольку α-частицы обладают громадной энергией и летят со скоростью несколько десятков тысяч километров в секунду, отражение αчастиц, их отклонение от прямого пути было неожиданным и удивило
всех. Передают, что Резерфорд, услышав о результатах этого опыта,
воскликнул: "Да ведь это все равно, как если бы пуля отскочила от листка бумаги!"
На основании опытов Гейгера и Марсдена Резерфорд пришел к выводу, что положительный заряд, имеющийся в атоме, в отличие от старых представлений, не размещен в нем равномерно, а сосредоточен в
малом объеме. Это является причиной очень высокой концентрации
положительного заряда в некоторых частях (собственно в ядре) атома.
Поэтому α-частица, несмотря на сравнительно большую массу (4 единицы) и огромную скорость, натолкнувшись на атомное ядро, отражается от него. При этом чем больше атомная масса элемента, тем чаще такие отражения происходят.
Расчеты, произведенные Резерфордом по результатам опытов с отражением α-частиц, показали, что атомное ядро по крайней мере в 100
тысяч раз (на 5 порядков) меньше по размерам, чем атом в целом. По
современным данным, величина диаметра атомного ядра имеет порядок
10-13 см, а величина диаметра атома – порядок 10-8 см, т.е. разница составляет пять порядков. Таким образом, Резерфорд в своем предварительном расчете соотношений размеров атомного ядра и атома в целом
получил величину, очень близкую к истинной.
Что мы знаем сейчас о строении атомного ядра? Хотя оно очень
мало по размерам, но с несомненностью установлена его сложность: в
192
нем есть составные части, которые, находясь в определенном соотношении и взаимодействуя друг с другом, определяют свойства и поведение
атомного ядра, а также атома в целом.
Атомные ядра состоят из двух типов нуклонов – ядерных протонов
(их число в конкретном атомном ядре равно Z) и ядерных нейтронов (их
число в конкретном атомном ядре равно N). В отличие от ядерных "свободные" (т.е. покинувшие атомное ядро) нейтроны неустойчивы и превращаются в протоны с периодом полураспада T1/2 = 12.5 мин:
1
1
→
+
e
+
ν
+
∆E
0n
1p
нейтрон
протон электрон антиэнергетика
нейтрино
Природа ядерных сил, удерживающих протоны и нейтроны в атомном ядре, окончательно не установлена. По-видимому, протоны и нейтроны взаимодействуют между собой за счет обмена примерно такого
же характера, как обмен электронами между атомами в ковалентных
молекулах. Однако в ядрах атомов вместо электронов на молекулярных
орбиталях действуют другие элементарные частицы и другие связывающие силы.
Стабилизация состояния нейтронов в ядре достигается, как полагают, за счет ядерных сил, обусловленных прежде всего обменом πмезонами (пионами) между ядерными протонами и нейтронами. Масса
π-мезонов всегда меньше массы протона и может достигать 200 масс
электронов.
В кислородных единицах (впрочем, они мало отличаются от углеродных) масса свободного протона – 1.0076, т.е. масса 10n больше, чем
масса 11p. Округляя эти цифры, мы будем условно принимать, что масса
протона и нейтрона равна единице.
При взаимодействии свободных нуклонов, сопровождающемся образованием атомного ядра, выделяется энергия, в миллионы раз превышающая энергию экзотермических химических реакций. Масса ядерного нуклона (протона или нейтрона в атомном ядре) меньше массы
свободного протона или нейтрона из-за выделения атомной энергии при
ядерном синтезе и выражается дробным числом. В то же время число
нуклонов (A) в атомном ядре равно сумме числа нейтронов (N) и протонов (Z): A = N + Z, эта величина – всегда целое число.
В научной литературе широко используется термин "нуклид", который обозначает атомные ядра (или атомы) с данным числом N и Z. Изобарные нуклиды имеют одинаковое число нуклонов (A = const): 9638Sr –
96
96
39Y – 40Zr. Изотопные нуклиды имеют Z=const и принадлежат, следо193
вательно, к одному и тому же химическому элементу: 23992U – 23592U –
236
238
36
37
38
92U –
92U. Изотопные нуклиды имеют N = const: 16S – 17Cl – 18Ar
39
40
– 19K – 20Ca. Изодиаферные нуклиды имеют одинаковый избыток
нейтронов (A – 2Z = N – Z = const). Наконец, изомерные нуклиды (изомеры) имеют одинаковые величины N и Z, но разное время распада
(примеры см. ниже).
Число A всегда целое и в точном выражении не равно атомной массе, которая выражается дробным числом. Существенное отклонение
точных величин атомных масс от целочисленных значений A=N+Z объясняется тем, что взаимодействие нуклонов (свободных протонов и нейтронов) сопровождается выделением энергии, в миллионы раз превышающей тепловые эффекты, наблюдаемые при химических реакциях.
При этом вступает в силу закон Эйнштейна, согласно которому масса
тела соответствует полному запасу его энергии, деленному на квадрат
скорости распространения света. Последняя величина равна 3 ⋅ 1010 см/с.
Массе 1 г, по уравнению Эйнштейна, отвечает энергия 9 > 1020 эрг, или
22 млрд ккал. Значит, если при какой-либо ядерной реакции масса реагирующих частиц уменьшится на 1 г ("дефект масс"), то выделится 22
млрд ккал.
Рассчитаем энергию реакции образования атомного ядра тяжелого
изотопа водорода: взаимодействуют протон и нейтрон с выделением
дейтона (ядро тяжелого водорода) и энергии. Сложением величин масс
протона (1.0076) и нейтрона (1.0090) получаем значение 2.0166. Такая
масса должна быть у дейтона, если бы он образовался без значительного
выделения энергии. Фактическая (экспериментально определенная) величина массы дейтона составляет 2.0142. Наблюдаемая разница между
рассчитанной и измеренной величинами составляет величину дефекта
массы, она равна 0.0024. Если убыли массы в 1 г соответствует выделение энергии в 22 млрд ккал, то убыли массы в 0.0024 г (1 моль дейтерия
D2) будет отвечать выделение 53 ⋅ 106 ккал. Следовательно, при синтезе
2 г дейтерия из нейтронов и протонов выделится 53 млн ккал.
Таким образом, выделение энергии, которым сопровождаются
ядерные реакции, на шесть порядков больше по величине, чем выделение энергии при химических реакциях. В первом случае это миллионы
килокалорий, во втором – десятки и сотни.
Рассчитаем теперь энергию образования ядра атома гелия. Сумма
масс двух протонов и двух нейтронов равна 4.0332 (теоретическая величина). Но действительная масса ядра атома гелия, как показывает массспектрометрический анализ, составляет величину 4.0017. Дефект массы,
194
таким образом, равен 0.0315. Умножая это значение на энергетический
эквивалент одного грамма массы, получаем громадную величину – 693
млн ккал. Таким образом, при ядерном синтезе гелия выделяется больше
энергии, чем в рассмотренном выше примере синтеза дейтерия. В связи
с этим большой интерес представляет изменение в ряду химических
элементов величин дефектов масс, отражающее зависимость разницы
между теоретически вычисленной и действительной массой более распространенных изотопов элементов от их атомного номера. Дефект массы, возникающий при образовании атомных ядер, растет от водорода до
железа, а потом убывает.
Использование атомной энергии делящегося урана основано на том,
что тяжелые атомные ядра, превращаясь в определенных условиях в
ядра легкие, выделяют очень большое количество энергии: разница между величинами дефекта массы для тяжелого ядра и суммарного дефекта масс "осколочных" ядер очень велика.
Тот же эффект используется и в случае, когда источником ядерной
энергии служат ядра наиболее легких атомных ядер, соединяющихся в
более тяжелое ядро. При таких ядерных реакциях выделяется особенно
много энергии потому, что дефект масс здесь наибольший (энергия связи для атомных ядер с Z > 5 составляет 7.4 – 8.8 МэВ). Действительно,
кривая дефектов масс показывает, что, хотя атомные ядра всех элементов образуются с выделением энергии, больше всего энергии выделяется
при образовании элементов средней части периодической системы. Поэтому можно использовать атомную энергию, выделяющуюся при образовании более тяжелых атомных ядер из самых легких, а также при распаде атомных ядер тяжелых элементов. В первом случае происходит
ядерный синтез, во втором – процесс деления тяжелых атомных ядер.
Соотношение числа нейтронов и протонов в атомном ядре подчиняется определенной закономерности. В 1932 г. советские физики Д.Д.
Иваненко и Е.Н. Гапон высказали предположение на основании рассмотрения свойств атомных ядер, что протоны и нейтроны стремятся
соединиться в равном числе: на один протон – один нейтрон. Это заключение особенно правильно для легких элементов, например, для He,
C, Si, O, отношение N/Z = 1.
Конечно, здесь речь идет об определенных изотопах элемента, чаще
всего о главных, наиболее стабильных, т.е. тех, которые доминируют в
природной плеяде его изотопов. Например, в плеяде водорода преобладает самый легкий изотоп 11H (99.98%). Более тяжелого изотопа – дейтерия 21D – только 0.02%. Таким образом, резко преобладает легкий
195
изотоп, и можно сделать вывод, что наиболее устойчивое атомное ядро
имеет изотоп 11H. При написании символа, обозначающего тот или иной
изотоп, в соответствии с предложением Ф. Жолио-Кюри, число нуклонов или округленное значение атомной массы и заряд ядра записывают
слева от символа элемента соответственно сверху и снизу: А = N + ZZЭ.
Например, изотоп урана обозначается как 23892U.
В естественной плеяде изотопов кислорода преобладает изотоп
16
8O, его атомное ядро наиболее устойчиво среди других изотопов кислорода.
Иногда количества изотопов в плеяде оказываются соизмеримыми
друг с другом. Например, на изотоп хлора 3517Cl в естественной плеяде
изотопов приходится 75.4%, а на изотоп 3717Cl – 24.6%. У брома это особенно ярко проявляется: изотопа с массой 79 – 50.6%, а с массой 81 –
49.4%. Однако чаще бывает, что один изотоп резко преобладает в естественной плеяде изотопов данного элемента. Величина N/Z = 1 уже для
элементов первого большого периода перестает быть характерной.
Для главного изотопа железа 5626Fe это соотношение равно 1.15, для
стронция – 1.33, для бария – 1.46, для 23892U – 1.6. О чем говорит этот
постепенный рост доли нейтронов по мере увеличения заряда ядра? Повидимому, в тяжелых атомных ядрах развиваются настолько большие
силы отталкивания между протонами, что изотопы с N/Z = 1 оказываются крайне неустойчивыми. Относительно стабильны только те изотопы
плеяды, в которых доля нейтронов достаточно велика. Нейтроны как бы
цементируют ядро – возникают дополнительные силы взаимодействия
нейтронов друг с другом и с протонами.
Для каждой области периодической системы существует свое условие устойчивости атомного ядра. Отклонение величины N/Z от значения, характерного для данного Z, приводит к меньшей распространенности такого изотопа, к его неустойчивости, радиоактивности.
Рассмотрим в качестве примера азот. Он имеет несколько изотопов.
Главный изотоп с округленным значением атомной массы, равным 14,
характеризуется соотношением N/Z=1. Содержание этого изотопа в
плеяде очень велико – 99.64%. У изотопа 157N на семь протонов приходится уже восемь нейтронов, и соотношение N/Z=1.14. Отклонение от
величины N/Z=1 приводит к резкому уменьшению содержания этого
изотопа в плеяде – всего 0.36%. Увеличение соотношения N/Z до 1.29 в
атомном ядре изотопа 167N приводит к потере стабильности – изотоп
радиоактивен (β-излучатель) и имеет период полураспада 7.5 с. У изотопа 177N на семь протонов приходится десять нейтронов. Этот изотоп
196
(тоже β-излучатель) может быть получен только искусственно, период
его полураспада составляет 4 с. Выбрасывая β-частицы, ядро атома 177N
уменьшает долю нейтронов, в нем содержащихся, что увеличивает его
стабильность.
Если теперь от изотопа 147N идти в сторону уменьшения соотношения N/Z, то вновь будет получено неустойчивое радиоактивное ядро –
изотоп 137N. Этот легкий изотоп, в отличие от тяжелых радиоактивных
изотопов азота, распадается, испуская позитроны (β-лучи).
Главный изотоп аргона – 4018Ar. Для него соотношение N/Z=1.22,
т.е. существенно отличается от единицы, хотя этот изотоп аргона вполне
стабилен. Следовательно, в этой области периодической системы располагаются элементы, стабильные изотопы которых характеризуются уже
заметным преобладанием числа нейтронов над числом протонов.
Уменьшение или увеличение числа нейтронов в атоме 147Ar вызывает уменьшение распространенности изотопа (его содержание в плеяде
падает) или проявление радиоактивности. Так, изотоп 4118Ar уже радиоактивен (T1/2=110 мин). Изотоп 4218Ar тоже радиоактивен, но устойчивость его выше: T1/2 = 3.5 года. Здесь мы сталкиваемся с проявлением в
плеяде изотопов своеобразной внутренней периодичности: четные по
массе изотопы 4018Ar и 4218Ar имеют несколько более прочные ядра, чем
нечетный по массе изотоп 4118Ar, хотя он ближе по величине соотношения N/Z к стабильному изотопу 4018Ar, чем другой четный изотоп 4218Ar.
Причиной такой своеобразной периодичности считают образование
в атомных ядрах из свободных протонов и нейтронов структурных единиц вторичного порядка. Одной из важнейших структурных единиц
атомных ядер является α – частица – ядро атома гелия, состоящее из
двух протонов и двух нейтронов, так называемый гелион. Другая возможная составная часть более сложных атомных ядер – дейтон – ядро
тяжелого изотопа водорода, состоящее каждое из одного протона и одного нейтрона: 21D.
Если атомное ядро имеет четный заряд (четный атомный номер), то
оно может быть построено только из гелионов, так как каждая пара протонов с таким же числом нейтронов образует гелион. Если же заряд ядра
нечетный, одному из протонов для образования гелиона не хватает парного протона. В этом случае в атомном ядре остается дейтон как вторичная структурная единица.
Как упоминалось, ядра гелия намного более прочны, чем ядра дейтерия, поскольку образуются с выделением гораздо большего количества энергии. Поэтому и атомные ядра, составленные из гелионов, проч197
нее, чем атомные ядра, включающие в свой состав дейтоны. Отсюда
следует важный вывод: элементы, у которых атомный номер четный,
образуют более прочные изотопы и обычно отличаются большей распространенностью в условиях Земли, чем элементы с нечетным атомным номером.
Это правило позволяет быстро ориентироваться, если нужно решить, какой из элементов более распространен. Например, железо (26Fe)
или кобальт (27Co)? Ясно, что железо, поскольку это четный элемент.
Число связанных в атомном ядре α-частиц (гелионов) можно определить по формуле Z/2. Кроме гелионов, атомное ядро четных элементов может содержать еще некоторое количество избыточных нейтронов.
Их число равно (округленной) атомной массе минус удвоенный атомный номер, т.е. 2Z. Например, в изотопе кислорода 168O число гелионов
равно 8/2 = 4, а в изотопе кремния 2814Si – 7. Оба ядра не содержат избыточных нейтронов и очень прочны. А вот в изотопе железа 5626Fe содержится 13 связанных гелионов, и, кроме того, в этом ядре имеется 56 – 26
⋅ 2 = 4 не связанных в гелионы нейтронов. Впрочем, это не понижает
стабильности атомных ядер железа, и на земном шаре железо по распространенности находится на первом месте.
Для нечетных элементов характерны сходные соотношения, однако
число гелионов следует определять по формуле: (Z – 1)/2 (единица – это
протон, который придает атомному ядру "нечетность", она должна быть
вычтена из величины атомного номера). Число дейтонов, о которых шла
речь выше, всегда равно единице. В каждом нечетном ядре может быть
только один связанный дейтон. Наконец, число избыточных нейтронов в
нечетных ядрах определяется по той же формуле, что и для четных: A –
2Z.
Вот несколько примеров нечетных ядер. В изотопе 2713Al число гелионов (13 – 1)/2 = 6, кроме того, имеется один дейтон. Разница A13⋅2=1, т.е. в ядре изотопа 2713Al имеется 6 гелионов, 1 дейтон и 1 избыточный нейтрон. Изотоп йода 12753I имеет 26 связанных α-частиц, 1 дейтон и 21 избыточный нейтрон. Отмеченные закономерности используются для классификации атомных ядер по величине их массы (так
называемый тип ядра по массе).
Следовательно, если массовое число изотопа делится на 4, то такой
изотоп будет наиболее распространенным по крайней мере в случае
четных элементов, поскольку такое ядро состоит из некоторого целого
числа гелионов. Такие ядра относятся к типу 4n, где n – некоторое целое
число. Например, атомное ядро изотопа кальция с массой 40 состоит из
198
10 гелионов (n=10). А вот массовое число (округленное значение атомной массы) главного изотопа никеля 5828Ni на 4 не делится. Ядро изотопа
58
Ni может быть составлено из 14 гелионов плюс еще две единицы массы. Это другой тип атомных ядер: 4n+2. Если сверх массы, приходящейся на гелионы, остается 3 единицы, то ядро по своей массе относится к
типу 4n+3. Такое атомное ядро имеет, например, 3517Cl. Сверх восьми
гелионов такое ядро может содержать, например, один дейтон и один
протон.
Наконец, существует еще один тип ядра по массе – это 4n+1. Такое
ядро имеет, например, изотоп 3717Cl. Для его массы 37 – наибольшее
число, делящееся на 4, это 36. Сверх этого числа остается только одна
единица массы.
На первый взгляд классификация атомных ядер по массе кажется
несколько примитивной. Однако она таит в себе глубокий смысл. Рассмотрение массовых чисел изотопов позволяет выявить важные закономерности. Так, можно показать, что все четные легкие элементы имеют
тип ядра по массе 4n (доминирующие стабильные изотопы). После железа, начиная с никеля, появляются доминирующие изотопы четных
элементов с типом ядра по массе 4n+2. С ростом атомного номера число
изотопов четных элементов с типом ядра по массе 4n+2 становится все
больше.
Есть только отдельные исключения: например, иридий – четный
элемент, но его главный изотоп имеет тип ядра по массе 4n+1. Азот –
нечетный элемент, а главный изотоп его имеет ядро с массой 14, т.е.
относится к типу 4n + 2. Однако, как говорится, исключения только подтверждают хорошее правило. Правило же состоит в том, что четные
элементы имеют главным образом ядра типа 4n или 4n + 2, а нечетные –
4n+3 или 4n+1. Из него следует важный вывод: четные элементы обычно имеют четное значение атомной массы. Нечетные (по атомному номеру) элементы имеют нечетную массу ядер главных изотопов. Например, кремний – четный элемент с атомным номером 14 имеет четное
массовое число 28, и, напротив, нечетный по атомному номеру фтор
имеет и нечетную массу главного единственного (стабильного) изотопа
19
9F.
Рассматривая элементы периодической системы, мы будем говорить не только об их химических, но и радиоактивных свойствах, поскольку последние часто не менее важны и интересны. В наши дни производство радиоактивных изотопов для некоторых элементов
становится более важным, чем производство стабильных изотопов. На199
пример, сейчас радиоактивный цезий изготовляется по стоимости продукции на значительно большую сумму, чем добывается из недр земли
обычного стабильного цезия. Не менее важна проблема обезвреживания
и захоронения радиоактивных отходов, разработки экологически безопасных методов использования радиоактивных изотопов и элементов,
например, при работе АЭС.
Типы и свойства радиоактивного излучения
Из курса средней школы известно, что имеются три основных типа
радиоактивного излучения: α-, β- и γ-лучи. α-лучи представляют собой
поток ядер гелия, β-лучи – поток электронов, γ-лучи – это электромагнитные кванты с малой длиной волны.
Например, радий, выбрасывая γ-частицу, превращается в радон.
Торий (изотоп 23490Th), выбрасывая β-частицу, превращается в протактиний. Такие же примеры можно привести и для искусственно получаемых изотопов. Так, изотоп 2411Na, который часто используется
как меченый атом, превращается в изотоп магния, выбрасывая βчастицу (отрицательно заряженный электрон). γ-излучение обычно
сопровождает радиоактивный распад с выбросом α- и β-частиц.
Кроме трех классических видов радиоактивности, есть и другие,
тоже часто встречающиеся. Например, при радиоактивном распаде ядро
искусственно получаемого изотопа азота 137N испускает позитрон (положительный электрон) и превращается в изотоп углерода 136C.
Иногда при радиоактивном распаде происходит втягивание в атомное ядро электрона с ближайшей к ядру электронной оболочки. Это так
называемый электронный захват, или "К-захват". Примером может служить превращение изотопа ванадия 4923V в изотоп титана 4922Ti, которое
происходит в результате захвата атомным ядром ванадия одного электрона с К-оболочки. При этом атомный номер элемента уменьшается на
единицу, хотя массовое число не изменяется.
В ряде случаев при радиоактивных превращениях образуются неустойчивые формы атомных ядер. Например, при облучении брома нейтронами образуется неустойчивый изотоп 8035Br, который затем претерпевает переход в более устойчивое состояние, излучая квант энергии.
При таком превращении ни масса, ни заряд ядра не меняются, но в
структуре ядра происходят изменения. Такое превращение называется
изомерным переходом (ИП).
200
Одно из самых важных явлений, связанных с радиоактивностью, –
это реакция деления атомных ядер. Например, изотоп урана 23592U, поглотив нейтрон, превращается в неустойчивый изотоп 23692U, который
как бы разваливается на две части, образуя "осколки": 14857La и 8535Br, и ,
кроме того, выделяет три избыточных нейтрона. Это отнюдь не единственный путь распада. Тот же изотоп 23692U может распадаться подругому: например, на ядра криптона и бария с одновременным высвобождением двух нейтронов. Однако при любом варианте деления ядра
урана на два осколочных ядра с меньшими атомными номерами происходит сопровождающееся выделением колоссального количества энергии смещение по кривой дефекта масс влево вверх, где расположены
элементы с меньшим относительным содержанием нейтронов в атомных
ядрах.
При рассмотрении ядерных превращений, а также ядерных реакций, полезно пользоваться так называемым правилом смещения, сформулированным в 1913 г. К.Фаянсом: при α-распаде заряд ядра уменьшается на две единицы, а атомная масса – на четыре. При β-распаде заряд
ядра увеличивается на единицу, а масса не меняется. При позитронном
распаде масса ядра также не меняется, а заряд ядра уменьшается на единицу. Наконец, при изомерном превращении не изменяются ни заряд, ни
масса ядра.
Электронный захват и позитронный распад имеют одинаковые последствия. Разница лишь в том, что электрон, внедряющийся в атомное
ядро при К-захвате, оставляет свободное место на к-электронной оболочке атома. На это место перескакивают электроны с наружных оболочек. В результате возникает характеристическое излучение с длиной
волны, отвечающей уже новому, а не исходному атомному ядру. В соответствии с правилом смещения элемент, испытывающий тот или иной
распад, смещается в периодической системе вправо или влево на две
или одну клетку (при ИП не смещается).
Для фиксации радиоактивного излучения и измерения его интенсивности пользуются счетчиками Гейгера – Мюллера различной конструкции. Обычно это алюминиевая трубка, внутри которой находится
специальная газовая смесь и по центру натянута вольфрамовая нить. К
вольфрамовой нити и алюминиевой оболочке счетчика приложена разность потенциалов порядка 2000 В. Когда радиоактивная частица через
тонкую алюминиевую оболочку попадает внутрь счетчика, она, обладая
высокой энергией, ионизирует газ, наполняющий счетчик, как говорят,
вызывает "ионную лавину".
201
Разряд быстро прекращается, так как при разряде разность потенциалов между W-нитью и Al-оболочкой счетчика резко уменьшается.
Однако, как только разряд прекращается, напряжение быстро возрастает, и новая радиоактивная частица вновь вызывает разряд. Электрические импульсы, возникающие при разряде, преобразуются в звук или
фиксируются цифровым табло. Счетчиком Гейгера измеряют число распадов в секунду. Конечно, это относительная скорость, так как число
регистрируемых импульсов зависит от конструкции счетчика, расположения образца и других факторов. Пересчет на абсолютную активность
ведут, используя эталоны.
Единицы, в которых измеряют радиоактивность, называются кюри
(Ки). 1 Ки соответствует 3.7 ⋅ 1010 расп/с – это скорость распада 1 г Ra.
В лабораторной практике, например, при работе с радиоактивными индикаторами, обычно имеют дело со значительно меньшей радиоактивностью. Соответственно активность таких препаратов измеряется в
меньших единицах: милликюри = 1 мКи = 10-3 Ки, микрокюри = 1 мкКи
= 10-6 Ки, нанокюри = 1 нКи = 10-9 Ки. В атомной промышленности,
напротив, имеют дело с большей радиоактивностью и используют более
крупные единицы: килокюри (103 Ки), мегакюри (106 Ки), гигакюри (109
Ки).
Интересно, что масса 1 Ки зависит от T1/2 радиоизотопа. Например,
препарат полония 210Po (T1/2 = 138.4 сут), имеющий активность 1 Ки,
весит 0.2 г, а такой же активности препарат изотопа плутония 239Pu (T1/2
= 24000 лет) весит 16 г, т.е. чем меньше T1/2, тем "легче" кюри. Один из
самых активных естественных изотопов – радон – дает активность 1 Ки,
будучи в очень маленьком количестве (1.65 мм3 – н.у.). Знаменитый геохимик В.И. Вернадский говорил, что, если бы радон можно было получить в чистом виде, не нашлось бы материала, который выдержал бы
температуру, развивающуюся при его распаде, – так активен радон.
Проникающую способность β-лучей удобно продемонстрировать,
используя изотоп 9038Sr, дающий жесткое β-излучение и имеющий удобную для практического использования изотопа величину T1/2 (≈25 лет).
Поднося к включенному счетчику препарат стронция-90, мы замечаем, что счетчик улавливает β-лучи уже на большом расстоянии. Когда
препарат поднесен к "окошку" счетчика вплотную, "треск" счетчика
становится сплошным, нельзя уловить отдельных разрядов, говорят, что
счетчик "захлебывается". Поставим перед счетчиком лист бумаги – он
практически не изменяет интенсивность излучения. Теперь закроем
счетчик, к которому поднесен источник β-лучей, листками алюминиевой
202
фольги. Чем толще слой алюминия, тем меньше мы слышим щелчков,
тем меньше β-частиц попадает в счетчик, так как радиоактивное излучение поглощается алюминием. Вот щелчки почти исчезли. Теперь снимем часть толстых алюминиевых пластинок, снова слышны щелчки,
снова β-частицы попадают в счетчик.
Если вместо алюминиевой пользоваться пластинкой из свинца, то
оказывается достаточно одной пластины, чтобы щелчки сразу исчезли.
Значит, β-частицы довольно легко поглощаются веществами с большой
атомной массой, а задерживающее действие веществ с малой плотностью (например, бумаги) очень мало.
γ-лучи поглощаются намного труднее, чем β-лучи. Источником γизлучения может служить радиоактивный изотоп 13755Cs. Поднесем ампулу с 13755Cs к счетчику – раздается очень сильный треск. Положим на
счетчик сразу все алюминиевые пластинки, которые в предыдущем опыте почти полностью задержали β-лучи – треск останется почти таким же
сильным. Положим и свинцовую пластину – эффект очень слабый. Еще
один лист свинца несколько уменьшит треск, но он все же еще очень
сильный. Поставим перед счетчиком стенку из толстых свинцовых кирпичей – только теперь γ-лучи поглощены. Плохая поглотимость γ-лучей
приводит к тому, что на γ-установках всегда приходится устанавливать
мощные поглотительные устройства – бетонные стены метровой толщины.
α-лучи обладают большой энергией, летят со скоростью 20 – 30
тыс. км/с, но из-за большой массы (ядра гелия) очень легко поглощаются различными веществами. В качестве α-излучателя воспользуемся
препаратом оксида плутония. α-частицы, излучаемые плутонием, фиксируются с помощью счетчика другой конструкции, нежели β- и γ-лучи
(с помощью так называемого фотоэлектрического счетчика). Достаточно самой тонкой алюминиевой пластины, чтобы задержать α-лучи.
Экспериментально можно убедиться в том, что в отличие от γлучей, α- и β-лучи несут заряд. Это можно показать на примере β-лучей.
Поместим ампулу с радиоактивным изотопом 9038Sr (β-излучателем) между полюсами лабораторного электромагнита. Когда магнит не включен, слышен треск – это β-частицы, попадая в счетчик ГейгераМюллера, фиксируются счетной установкой. После включения магнита
треск смолкает, поскольку магнит отклоняет β-частицы от прямолинейного пути, и они не попадают в счетчик.
203
Проделаем то же самое с γ-излучением. Для этого между полюсами
магнита поместим ампулу с 13755Cs. При включенном магните счетчик
фиксирует сильное γ-излучение. Выключение магнита не дает никаких
изменений, счетчик по-прежнему продолжает фиксировать сильный поток γ-лучей. Выключим магнит – все остается, как было. Следовательно,
γ-лучи свободно, не отклоняясь, проходят между полюсами магнита, т.е.
зарядом не обладают.
Радиоактивное излучение обладает способностью ионизировать окружающий воздух. Это свойство можно показать на простом приборе. К
металлическому стержню, укрепленному на изолирующей подставке,
прикреплены тонкие полоски бумаги в виде султана. Если наэлектризовать эбонитовую палочку трением и зарядить металлический стержень,
бумажки, с ним скрепленные, разойдутся в разные стороны из-за взаимного отталкивания, так сказать, встанут дыбом. Поднесем к султану радиоактивное вещество, например, эмаль, содержащую β-излучатель, –
изотоп прометия 14761Pm. Султан быстро опадает, бумажки перестают
отталкиваться друг от друга и от стержня. При повторении опыта происходит все то же самое.
Описанное явление имеет важное практическое применение: когда
производится прядение волокон, особенно искусственных, возникают
заряды статического электричества, которые запутывают волокна. При
повышении электропроводности воздуха электростатические заряды
быстро стекают с волокон, не накапливаясь на них и не вызывая их спутывания. Таким нейтрализатором статических зарядов служит радиоактивный препарат, ионизирующий окружающий его воздух и способствующий увеличению его электропроводности.
Способность радиоактивных лучей ионизировать воздух можно
продемонстрировать с помощью электроскопа. Зарядим его эбонитовой
палочкой через металлический шарик, имеющийся в верхней части
электроскопа. Стрелка прибора указывает, что он заряжен. Изоляция не
позволяет электрическим зарядам стекать в землю через подставку, а
воздух в обычных условиях мало электропроводен. Приблизив сюда
радиоактивный препарат, увидим, что стрелка электроскопа быстро возвращается на нуль – электроскоп разрядился через воздух, ионизированный радиоактивным излучением.
Практически важным свойством является также действие радиоактивного излучения на некоторые вещества, способные светиться. Приблизив к эмали, содержащей радиоактивный 14761Pm (β-излучатель), экран с веществом, способным светиться, мы наблюдаем появление сине204
зеленого свечения. Радиоактивное излучение действует также на светочувствительные материалы, такие как фотобумага, фотопленки и т.д.
Фотоматериалы под действием радиоактивного излучения чернеют (светочувствительное вещество разрушается). Это их свойство используется
для изготовления простейших счетчиков индивидуального пользования
для работающих с радиоактивностью.
Контрольные вопросы
1. Что представляют собой α, β и γ-лучи? Какие из них являются
частицами?
2. Чем отличаются модели Томсона и Резерфорда?
3. В чем планетарная модель атома Резерфорда не согласуется с
представлениями классической физики?
4. В чем сущность "ультрафиолетовой катастрофы", и как Планку
удалось разрешить этот парадокс?
5. Приведите эмпирическую формулу для расчета спектральных линий атома водорода, предложенную Бальмером. Как её объяснил
Бор?
6. В чем заключается квантование энергии?
7. Как объяснить, что один и тот же атом водорода может последовательно испустить фотоны, соответствующие сериям линий
Лаймона, Пашена, Бреккета, Бальмера, Пфунда?
8. В чем заключаются недостатки модели атома Бора?
9. Почему волновые свойства обнаруживаются у пучков микрочастиц и не обнаруживаются у пуль, выпущенных из автомата?
10. В чем суть гипотезы де Бройля?
11. Почему в повседневной жизни мы не принимаем во внимание
принцип неопределенности?
205
12. Какие свойства характерны для волновой функции, описывающей
состояние электрона в атоме?
13. Какие три квантовых числа появляются в решении уравнения
Шредингера для атома водорода? В чем их физический смысл?
14. Почему главное квантовое число n не может принимать значения,
равные нулю?
15. Что такое атомная орбиталь? Чем она отличается от орбиты Бора?
16. Какие электронные состояния называются основными?
17. Чем отличается форма р-орбиталей от d-орбиталей?
18. Какие электронные состояния называются "вырожденными"?
19. Почему оказалось возможным применить положения, разработанные для атома водорода, для многоэлектронных атомов?
20. Согласно каким правилам идет заполнение электронных оболочек в многоэлектронных атомах?
21. В чем причина заполнения 3d-подуровня после 4s-подуровня?
22. Какое квантовое число не имеет аналогов в классической механике?
23. Почему происходит "провал" электрона на нижележащий подуровень в электронных конфигурациях хрома, меди, серебра, золота?
24. В чем суть правила Клечковского?
25. Что называется узловой поверхностью атомной орбитали?
26. Как связаны главное и орбитальное квантовые числа с числом узловых поверхностей атомной орбитали?
27. Какова максимальная емкость электронного уровня? Чем она определяется?
28. Какие орбитали являются кайносимметричными? Чем кайносимметричные орбитали отличаются от проникающих орбиталей?
29. Каков физический смысл величины Ψ2?
30. Что называется термом атома?
Задачи
1. Вычислите длину волны фотона с частотой 1,2 ⋅ 1015 Гц. Какова
его энергия в килоджоулях на моль?
2. Вычислите энергию фотонов, соответствующих радиоволнам на
частоте 1000 килогерц, выразив её в килоджоулях на моль.
3. Какова длина волны фотонов с энергией 347 кДж/моль?
206
4. Первая энергия ионизации атомов цезия равна 376 кДж/моль.
Вычислите первую энергию ионизации одного атома цезия (в килоджоулях и электронвольтах).
5. Изобразите пространственное распределение следующих орбиталей с квантовыми числами: n = 2, l = 1; n = 1, l = 0.
6. Электрон находится на одной из 3d-орбиталей. Какие значения
квантовых чисел n, l, m характеризуют этот электрон?
7. Объясните, почему существуют ионы H , Cl , Au и не существуют ионы He , Ne , Ca .
8. Составьте электронные формулы элементов в указанной степени
окисления: P+I, Ti+III, Cr+IV, Se-II. Какие из них будут диамагнитными, а какие парамагнитными?
9. Укажите внешние электронные подуровни в следующих электронных формулах нейтральных атомов: 1s22s1; 1s22s22p63s2;
1s22s22p63s23p63d24s2; 1s22s22p1. Какой смысл вкладывается в термин "внешний электронный подуровень"?
10. Укажите, что является общим в электронном строении для каждого набора атомов в указанной степени окисления: C-IV, N-III,
Mg+II, Ne0, O-II, Na+I, F-I.
207
ПЕРИОДИЧЕСКИЙ ЗАКОН И ПЕРИОДИЧЕСКАЯ
СИСТЕМА ЭЛЕМЕНТОВ
История создания периодического закона
Поиски классификаций химических элементов и их систематизации
начались задолго до открытия периодического закона. Но на пути ученых в этой области встречались значительные трудности: недостаток
экспериментальных данных по числу химических элементов, по их характеристикам (значения атомных масс были неточны). В 1829 г. И. Деберейнер сделал попытку систематизировать химические элементы с
помощью атомных масс. Он заметил, что некоторые элементы, сходные
по свойствам, можно объединить в группы по три элемента. Эти группы
он назвал триадами.
Li
Na
K
Ca
Sr
Ba
Cl
Br
I
S
Se
Te и др.
Особенность триад Деберейнера состояла в том, что атомная масса
среднего элемента была близка к полусумме атомных масс двух других
элементов триады. Триады Деберейнера можно представить прообразом
групп в периодической системе Менделеева. Но это представление
слишком несовершенно. Искусственным ограничением элементов триадами является невключение в число элементов аналогов магния в семейство Ca, Sr, Ba и кислорода в семейство S, Se, Te, сходных по свойствам
со своими аналогами. Деберейнер видел аналогии в свойствах фосфора,
мышьяка, сурьмы и висмута, но, ограничив себя поисками триад, не
смог найти верного решения.
В начале 60-х гг. ХIХ в. появилось несколько работ, посвященных
систематизации элементов. А. де Шанкуртуа располагал все известные
элементы в порядке возрастания их атомных масс. Полученный ряд он
наносил на поверхность цилиндра по линии, исходящей из его основания под углом 45° и плоскости основания (спираль Шанкуртуа). При
развертывании поверхности цилиндра оказывалось, что на вертикальных линиях, параллельных оси цилиндра, находились элементы, сходные по химическим свойствам. Так, на одну вертикаль попадали Li, Na,
K; Be, Mg, Ca; O, S, Se, Te и т.д. Но несовершенство спирали Шанкуртуа
проявляется в том, что в одну группу вместе с близкими по свойствам
элементами попадали элементы, резко отличающиеся по химическим
208
свойствам. В одну группу со щелочными металлами попадал марганец, в
группу кислорода и серы попадал титан.
После де Шанкуртуа английский ученый Д. Ньюлендс также сделал
попытку сопоставить химические свойства элементов с их атомными
массами. Он, расположив элементы в ряд по возрастанию атомных масс,
заметил сходства, проявленные каждым восьмым элементом. Найденную закономерность Ньюлендс назвал законом октав по аналогии с семью интервалами музыкальной гаммы. В своей таблице он располагал
элементы в вертикальные группы по семь элементов в каждой. При этом
он обнаружил, что сходные по химическим свойствам элементы оказываются на одной горизонтальной линии. Ньюлендс первым дал ряд элементов, расположенных в порядке возрастания атомных масс, присвоил
химическим элементам соответствующий порядковый номер, заметил
систематическое соотношение между порядковым номером и физикохимическими свойствами.
Почти сразу же после работ Ньюлендса появляется таблица Одлинга, в которой впервые элементы объединены в совокупности по признаку общности химических свойств:
Li, Be, B, C, N, O, F.
Na, Mg, Al, Si, P.
K, Ca, TI, Cr, Mn.
Hg, Tl, Pb, Bi и т.д.
Эти ряды очень похожи на фрагменты периодической системы
Менделеева. Но Одлинг не сумел сделать обобщающих выводов из своей работы. Кроме того, в его таблице ряды и группы химических элементов остались изолированными друг от друга, не объединенными каким-либо общим принципом.
Фундаментальные принципы систематизации элементов создал
Д.И. Менделеев в марте 1869 г. Спустя несколько месяцев, в декабре
1869 г, немецкий ученый Л. Майер опубликовал таблицу химических
элементов, также отражающую периодичность в изменении свойств
элементов в зависимости от их атомных масс.
Авторская формулировка периодического закона следующая:
"Свойства простых веществ, а также формы и свойства соединений
элементов, находятся в периодической зависимости от 4 атомных
весов элементов". Но Менделеев лучше своих современников понимал,
что основополагающей характеристикой элементов является не атомная
масса, а какое-то более важное внутреннее свойство атома. Этим можно
объяснить распределение химических элементов в периодической сис209
теме с нарушением последовательности увеличения атомных масс (Ar –
K, Co – Ni, Te – I).
После открытия электрона и разработки теории строения ядра атома голландский физик А. Ван ден Брук в 1911 г. высказал предположение, что заряд атома того или иного элемента равен порядковому номеру элемента в периодической системе. Эта гипотеза получила
экспериментальное подтверждение в работах физика Г. Мозли, который
установил, что порядковые номера элементов действительно соответствуют значениям ядерных зарядов их атомов. После работ Г. Мозли стало
ясно, что элементы в периодической системе располагаются в порядке
возрастания зарядов ядер атомов. В настоящее время периодический
закон формулируется следующим образом: "Свойства простых веществ, а также формы и свойства соединений элементов, находятся
в периодической зависимости от зарядов ядер атомов элементов".
Приоритет Д.И. Менделеева в открытии
периодического закона
Д.И. Менделеев (1869 г.) так формулировал периодический закон:
"Свойства простых тел, а также формы и свойства (сложных) соединений находятся в периодической зависимости от величины
атомных весов элементов".
Периодический закон, как известно, имел и имеет "предсказательную" силу. Менделеев предсказал не известные тогда элементы и их
свойства.
В 1869 г. Менделеев писал: "Должно ожидать открытия многих еще
не известных простых тел, например, сходных с алюминием и кремнием
элементов с паем (т.е. с атомным весом) 65 и 75". Два года спустя, в
1871 г., Менделеев более подробно описал свойства еще не открытых
элементов – аналогов бора, алюминия и кремния. Он назвал их "экабор",
"экаалюминий", "экасилиций" (приставка "эка" взята из санскритского
древнеиндийского языка и означает "один"; так "экасилиций" – первый
аналог кремния и т.п.).
В своих воспоминаниях Менделеев так отзывался об этой своей работе: "Это (предсказание свойств) есть более подробное развитие, но я
решил тогда его сделать, чтобы тем утвердить периодичность элементов. Это был риск, но правильный и успешный". Пример Менделеева
показывает, таким образом, что в науке можно и нужно рисковать, если
научная убежденность позволяет это сделать.
210
Менделеев предсказал не только галлий (Ga – "экаалюминий"),
скандий (Sc – "экабор") и германий (Ge – "экасилиций"), но и не известные тогда аналоги цезия – франций, бария – радий, тантала – протактиний и другие элементы. Быстро оправдались предсказания относительно
Ga, Ge, Sc. В 1875 г. Лекок де Буабодран (Франция) открыл галлий, в
1879 г. в Скандинавии Нильсоном был открыт скандий, и в 1881 г. в
Германии Винклер открыл германий.
Периодический закон послужил важной основой для открытия других элементов, таких как гафний (открыт уже в ХХ в.), рений, протактиний: поиски этих элементов велись с использованием химической аналогии, вытекающей из периодического закона. Периодический закон
сыграл также важную роль и в идентификации искусственно синтезированных элементов.
Не менее важным, чем предсказание еще не открытых элементов,
было исправление Менделеевым на основе периодического закона
атомных весов и валентностей большого числа элементов. Это относится не только к редкоземельным элементам, хотя и в данной области
вклад Менделеева в развитие периодического закона трудно переоценить. Менделеев исправил неправильно определенные атомные веса
бериллия (его до Менделеева считали трехвалентным), индия, урана,
тория и др. Такие исправления позволили правильно определить место
элемента в периодической системе и тем самым еще более "укрепить"
(как говорил Менделеев) периодический закон.
Менделеевский закон заслужил всемирное признание, подтверждений этому много. Так, например, авторы, открывшие элемент №101 –
американские ученые Гиорсо, Харве и другие – в знак уважения к Менделееву в 1955 г. дали этому элементу название "менделеевий" (теперь
говорят и пишут "менделевий" с одним "е"). Они писали, что это сделано в признание ведущей роли великого русского химика Дмитрия Менделеева, который первым использовал периодический закон для предсказания свойств еще не открытых элементов, и в частности, дал ключ к
открытию трансурановых элементов – актиноидов.
Яркой иллюстрацией признания роли Менделеева в открытии новых элементов явилось празднование в 1969 г. 100-летия периодического закона. Все химики мира отмечали этот юбилей. Сиборг, которому
принадлежит честь получения и идентификации большого количества
трансурановых элементов, участвовал в торжествах ЮНЕСКО в Париже
в марте 1969 г., был на Менделеевском симпозиуме Американского химического общества в апреле 1969 г., выступал на конгрессе в честь
211
100-летия периодического закона в Ленинграде и , наконец, председательствовал на симпозиуме в честь открытия Менделеева в ноябре 1969
г. в Хьюстоне (Техас, США). Сиборг писал: "В докладах, сделанных
ранее, на других научных собраниях, посвященных развитию периодической системы, я подчеркивал, что элегантная простота периодической
таблицы Менделеева заставила физиков и химиков продолжать поиски
взаимосвязей между химическими свойствами элементов".
Большинство наших современников признают непреходящую важность открытия Менделеева, преклоняются перед его гением. Однако
многие зарубежные историки химии приписывают все же открытие периодического закона не одному Менделееву, но и немецкому химику Л.
Майеру, который будто бы "одновременно и независимо от Менделеева" пришел к тем же положениям периодического закона.
Такого рода утверждения являются искажением истины. В действительности ход событий был следующим. Менделеев сообщил об открытии периодического закона 1 марта 1869 г. (на съезде русских естествоиспытателей и врачей). Тогда же он написал статью о периодическом
законе и направил ее в печать. Майер опубликовал в "Анналах Либиха"
в 1870 г. статью (послана в печать в декабре 1869 г.), в которой толковал
о том же предмете. В этой статье (1870 г.) Майер ссылается на доклад
Менделеева, который был ему знаком по реферату. Майер пишет: "Следующая таблица в существенных чертах тождественна той, которую
дает Менделеев".
До момента, когда Майер познакомился с докладом Менделеева, он
не высказывал идею периодичности. Так, в ранее опубликованной статье (от 1864 г.) не было еще речи о тех закономерностях, которые нашел
Менделеев, не рассматривалась зависимость каких-либо свойств элементов от атомного веса.
Выдающийся русский химик Л.А. Чугаев пишет: "До статьи Менделеева идея периодичного чередования свойств элементов при расположении их в зависимости от атомного веса была совершенно чуждой
Майеру – эти выводы были впервые почерпнуты им у Менделеева".
Только после доклада Менделеева Майер предложил свою хорошо известную кривую зависимости атомных объемов элементов от их атомного веса. До знакомства с докладом Менделеева Майер лишь группировал элементы по их валентности и разнице в атомных весах между
рядами.
212
Таким образом, приоритет Менделеева в открытии периодического
закона не вызывает сомнений, он признается всеми, кто знаком с историей его создания и развития.
Периодический закон, открытый Менделеевым, оставаясь неизменным в своей основе, претерпевает развитие и усовершенствование по
мере расширения и обновления наших знаний о природе вещества.
В начале ХХ в. наука о веществе сделала громадный скачок в связи
с разработкой ядерной теории строения атомов, экспериментальным
определением величин зарядов, атомных ядер и электрона (Мозли,
Томпсон, Резерфорд, Бор и др., 1911 – 1914). Оказалось, что заряд
атомного ядра совпадает с порядковым номером элемента в периодической системе. Если атом элемента находится в электронейтральном состоянии, атомное ядро с положительным зарядом Z окружено таким же
количеством электронов, каждый из которых несет единицу отрицательного заряда.
Поскольку стало ясно, что именно заряд ядра определяет индивидуальность химических элементов, а атомный вес (атомная масса) элемента является величиной, зависящей от заряда ядра, изменилась и формулировка периодического закона. Современная формулировка состоит в
следующем:
"Физические и химические свойства простых веществ, а также
формы и свойства сложных соединений находятся в периодической
зависимости от величины заряда ядра атомов".
Введение новой формулировки не означает, что старая неверна и
может быть отброшена. Действительно, между величинами атомных
весов и атомным номером (или зарядом ядра атома) имеется определенная связь: атомный вес (А) примерно в 2 – 2.5 раза больше величины
атомного номера Z.
Число нуклонов A = Z+N, где N – число нейтронов, относится к
числу протонов Z как А/Z ≈ 2. Для многих элементов начала периодической системы (от 42He до 168O) это отношение довольно точно равно 2,
начиная с железа оно увеличивается от 2.1 у Fe до 2.5 у Hg и 2.6 у U.
(Увеличение числа протонов в ядрах тяжелых атомов требует увеличения числа нейтронов для того, чтобы ядро не распалось из-за отталкивания протонов, не "разбавленных" необходимым количеством нейтронов). Но все же это отношение, зависящее от соотношения числа
протонов и нейтронов в атомном ядре, близко к 2 и сохраняется примерно постоянным для всех элементов периодической системы. Следовательно, A – атомный вес (округленная величина A – число нуклонов) и
213
Z – заряд атомного ядра – величины, находящиеся в прямой зависимости друг от друга. Поэтому Менделеев не сделал никакой ошибки, когда
взял за основную характеристику элемента атомный вес. Сейчас мы знаем, что эта величина прямо пропорциональна заряду атомного ядра (закон Мозли, 1913 г.) Мы также знаем, что причиной периодического изменения химических свойств элементов является периодически
изменяющееся строение электронных оболочек атомов.
Менделеев совершил свое великое открытие в то время, когда
сколько-нибудь определенные представления о строении атома еще отсутствовали. Надо было обладать поистине титанической силой предвидения, интуицией гения для того, чтобы в те времена сформулировать
периодический закон. Для самого Менделеева причины периодичности
в изменении химических свойств элементов не были ясны. Он писал в
одной из работ: "Самым таинственным для нас пока явлением представляется периодичность".
Формы периодической таблицы. Развитие периодической
системы Д.И. Менделеева
Менделеев предложил несколько способов построения, несколько
форм периодической таблицы. Первым был "вертикальный вариант",
где периоды располагались в виде вертикальных столбцов. В 1871 г.
Менделеев заменил вертикальный вариант таблицы "горизонтальным"
вариантом, так называемой короткой формой. Первый период ("предварительный") и два малых периода в короткой форме периодической системы занимают по одной горизонтальной строке, а большие периоды –
по две строки. В наши дни принцип короткой формы является наиболее
употребительным, но используется и "длинная" форма таблицы, также
предложенная самим Менделеевым. В длинной форме большие периоды
так же, как и малые, занимают только одну горизонтальную строку. В
средней части строк больших периодов располагаются так называемые
переходные элементы, а непереходные элементы разорваны на две
группы и размещаются слева и справа от переходных.
В последнем прижизненном издании "Основ химии" Менделеева
им приведена как наиболее удобная для химиков короткая форма, отличающаяся от современных вариантов таблиц главным образом тем, что в
ней было еще много пустых клеток, которые позже были заполнены
вновь открытыми элементами. Кроме того, во времена Менделеева еще
не был окончательно решен вопрос о расположении в периодической
214
системе редкоземельных элементов, а группы актинидов практически
еще не существовало.
Значительные изменения периодическая таблица претерпела только
в связи с открытием трансурановых элементов. Проблема их размещения в периодической системе решается неоднозначно. Сиборг выдвинул
гипотезу, согласно которой существует аналогия между лантанидами и
актинидами – элементами, следующими за актинием. При этом предполагается, что электронная оболочка атомов актинидов формируется путем заполнения глубоколежащего 5f-электронного подуровня, и, начиная с урана, актиниды понижают характерную для них (высокую до
урана включительно) степень окисления, становясь, как лантаниды, преимущественно трехвалентными в своих соединениях. Число актинидов,
по Сиборгу, должно быть равно числу лантанидов, т.е. 14. Вслед за последним элементом ряда актинидов (Lr, №103) должны располагаться
элементы со свойствами, сходными со свойствами гафния (его тяжелый
аналог – элемент №104) и, затем, тантала (его аналог – №105) и т.д.
Гипотеза Сиборга имеет много сторонников. В публикуемых сейчас
вариантах периодической системы актиниды, так же как и лантаниды,
помещают в одну клетку с родоначальником ряда – актинием, а расшифровка ряда дается в особой строке в нижней части периодической
таблицы. В то же время часто актинидная гипотеза трактуется неверно.
Ряд авторов настаивают необоснованно на полной аналогии актинидов и
лантанидов. Действительно, даже самое общее знакомство с химическими свойствами элементов начала ряда актинидов – Th, U, Np, Pu –
указывает на принципиальные отличия в свойствах актинидов и лантанидов. Так, для лантанидов наиболее характерна степень окисления (III),
тогда как упомянутые актиниды устойчивы в более высоких степенях
окисления (IV, VI).
В последнее время работами сотрудников Института физической
химии АН СССР показано, что Np и Pu (в отличие от предсказаний актинидной гипотезы) могут быть получены в состоянии окисления (VII),
т.е. возможная для них высшая степень окисления не ниже, а выше, чем
у урана. Синтезировано 20 твердых соединений Np, Pu (VII). В отличие
от актинидов максимальная степень окисления для лантанидов – (IV).
Она реализуется только при проведении синтеза в жестких условиях и
только у Ce, Pr и Tb. Таким образом, разница в химических свойствах и,
следовательно, в электронном строении атомов этих групп элементов
является очень существенной. Согласно В.И. Гольданскому, энергетика
электронных состояний атомов лантанидов и актинидов различна благо215
даря релятивистским эффектам и спин-орбитальному взаимодействию.
Например, для лоуренсия состояние 7s27p1 выгоднее, на 0.5 эВ, чем состояние 6d17s2, аналогичное состоянию "последнего" лантанида лютеция. Таким образом, лоуренсий больше похож на p-элемент, чем на dэлемент (аналог лютеция). "Смешение" (гибридизация) 5f-, 6d-, 7s-, 7pэлектронных состояний у трансурановых элементов, следовательно, является очень существенным, что исключает сколько-нибудь полную
аналогию в свойствах актинидов (по крайней мере, членов первой половины ряда) и лантанидов.
В то же время для второй половины ряда аналогия в свойствах актинидов и лантанидов часто проявляется, и в наши дни все еще продолжаются поиски фактов, говорящих в пользу актинидной гипотезы. Так,
Иво Звара (Институт в Дубне) сообщил о дополнительных доказательствах того, что элементы №104 и №105 (курчатовий и нильсборий) являются тяжелыми аналогами соответственно гафния и тантала, т.е. принадлежат к IV и V группам периодической системы и следуют
непосредственно за актинидной группой 5f-элементов. Доказательством
сходства элемента №104 с гафнием было экспериментальное обнаружение большей летучести безводного хлорида курчатовия по сравнению с
такими же хлоридами лантанидов (III). Как пишет Гольданский, "хватило всего 16 атомов курчатовия, чтобы доказать, что №104 уже входит в
IV группу периодической системы и что, таким образом, в соответствии
с актинидной теорией элементом №103 завершается заполнение 5fоболочки".
Звара показал, кроме того, что хлорид нильсбория (Ns, №105) более
летуч, чем HfCl4, но менее летуч, чем NbCl5. Именно такими свойствами
должен был обладать хлорид экатантала. Этот эксперимент также был
проведен на нескольких атомах Ns, причем период полураспада изотопа
Ns составлял всего несколько секунд.
В какой мере описанные в литературе эксперименты свободны от
ошибок, покажет будущее. Во всяком случае, очень интересен тот факт,
что идентификация трансуранов, полученных с использованием сложных физических приборов, проводится затем на основе закономерностей, вытекающих из периодического закона, химическими методами,
которые для столь малого числа атомов вновь синтезированных элементов оказываются более надежными, чем методы физической идентификации.
Структура периодической системы
216
Расположение химических элементов в периодической системе отражается в виде горизонтальных и вертикальных рядов; периодов и
групп.
Период – последовательный ряд элементов, в атомах которых происходит заполнение одинакового числа квантовых слоев. При этом номер периода элемента совпадает со значением главного квантового числа n внешнего слоя.
Элементы в периодах делятся на семейства: s-элементы, pэлементы, d-элементы и f-элементы.
Если главное квантовое число определяет положение элемента в
периоде, то сочетание l, m, s – квантовых чисел определяет положение
элемента в соответствующей группе периодической системы. В соответствии с максимальным числом электронов на внешнем слое элементы
периодической системы подразделены на восемь групп. Подразделение
на группы производится по числу валентных электронов.
Положение в группах s- и p-элементов определяется числом электронов внешнего слоя; фосфор (3s23p) имеет на внешнем слое 5 электронов и относится к пятой группе, аргон (3s23p6) – к восьмой группе.
Положение в группах d-элементов обусловливается общим числом
валентных s-электронов и d-электронов предвнешнего слоя. По этому
признаку первые шесть элементов каждого семейства d-элементов располагаются в одной из соответствующих групп: Sc (3d14s2) – в третьей
группе, Mn (3d54s2) – в седьмой группе. Цинк, у которого предвнешний
слой завершен и валентными являются 4s2-электроны, относится ко второй группе.
По наличию на внешнем слое лишь одного электрона за счет "провала" одного из s-электронов в d-подуровень Cu (3d104s2), Ag (4d105s1),
Au (5d106s1) относят к первой группе. Co (3d74s2), Ni (3d84s2), Rh (4d8s1),
Pd (4d10), Ir (5d76s2), Pt (5d96s1) оказываются вне групп периодической
системы. Их вместе с Fe, Ru, и Os обычно помещают в восьмую группу.
В соответствии с особенностями электронных структур 4f-элементы
и 5f-элементы помещают в третью группу.
Элементы групп делятся на подгруппы: s- и p-элементы составляют
главную, а d-элементы – побочную подгруппы.
Кроме того, часто в особую подгруппу так называемых типических
элементов выделяют элементы малых периодов. В этом случае, согласно
Б.В. Некрасову, элементы группы подразделяются на три подгруппы:
типические элементы и две подгруппы, составленные из элементов
больших периодов.
217
Пример: группа состоит из следующих подгрупп:
Типические элементы:
C
Si
1s22s22p2
1s22s22p63s23p2
Элементы подгруппы Ge:
Ge
Sn
Pb
[Ar]3d104s24p2
[Kr]4d105s25p2
[Xe]4f145d106s26p2
Элементы подгруппы Ti:
Ti
Zr
Hf
[Ar]3d24s2
[Kr]4d25s2
[Xe]4f145d26s2.
Все свойства элементов, определяемые структурой валентных квантовых слоев, закономерно изменяются по периодам и группам системы.
При этом, поскольку в ряду элементов-аналогов электронные структуры
сходны, но не тождественны, то при переходе от одного элемента к другому в группах и подгруппах наблюдается не простое повторение
свойств, а их более или менее отчетливо выраженное закономерное изменение. Поскольку орбитали атомов заполняются сначала по одному, а
затем по второму электрону, на фоне общей периодичности и изменения
свойств элементов в периодах наблюдается еще так называемая вторичная периодичность (открыто Е.В. Бироном (Россия) 1915 г.; объяснено
С.А. Щукаревым).
Энергия ионизации и сродство к электрону
Химическая природа элемента может быть оценена способностью
его атома терять и приобретать электроны. Эта способность оценивается
энергией ионизации атома и его сродством к электрону.
Энергией ионизации называется количество энергии, необходимое для отрыва одного электрона от невозбужденного атома.
Энергия ионизации выражается в кДж/моль или в эВ/атом.
Кривая зависимости изменения энергии ионизации в зависимости
от порядкового номера элемента имеет ярко выраженный периодический характер. Наименьшей энергией ионизации обладают s-элементы
(3 – 5 эВ): Li – 5.39 эВ, Na – 5.14 эВ, K – 4.34 эВ, Rb – 4.18 эВ вследствие сильного экранирования заряда ядра внутренними электронами.
Наибольшей энергией ионизации обладают p-элементы восьмой группы.
Возрастание энергии ионизации по периоду обусловливается возраста218
нием эффективного заряда ядра: Li – 5.39 эВ, Be – 9.32 эВ, B – 8.30 эВ,
C – 11.26 эВ, N – 14.53 эВ, 0 – 13.6 эВ, F – 17.2 эВ.
На возрастающих участках кривой значений энергий ионизации наблюдаются небольшие максимумы, отражающие явление вторичной
периодичности. Так, максимумы, соответствующие элементам, у которых внешние подслои заполнены полностью s2 (Be, Mg, Zn) или наполовину р3 (N, P, As), свидетельствуют о повышенной устойчивости подобных конфигураций. В соответствии с особенностями электронного
строения d- и f-семейств потенциалы близки.
Sc
Ti
V
Cr
3d14s2
3d24s2
3d34s2
3d54s1
I1, эВ
6.56
6.83
6.74
6.76
В подгруппах s- и р-элементов с увеличением атомного номера потенциалы ионизации в общем уменьшаются, тогда как в подгруппах dэлементов при одинаковом увеличении заряда ядра потенциалы увеличиваются.
p-элементы d-элементы
I, эВ
As 9.81
Sb 8.64
Bi 7.29
I, эВ
V 6.74
Nb 6.88
Ta 7.88
Уменьшение потенциалов ионизации в подгруппах s- и p-элементов
объясняется увеличивающимся (по мере увеличения числа электронных
слоев) экранированием заряда ядра электронами, предшествующими
внешним электронам.
Повышение же потенциала ионизации у d-элементов в подгруппах
можно объяснить эффектом проникновения электронов к ядру. Этот
эффект обусловлен тем, что, согласно квантовой механике, все электроны (даже внешние) определенную долю времени находятся в области,
близкой к ядру. Поэтому можно сказать, что внешние электроны проникают к ядру через слои внутренних электронов. При этом концентрация
электронной плотности в непосредственной близости от ядра при одном
219
и том же n – наибольшая для s-электронов, менее для p-электронов, еще
меньше для d-электронов. Эффект проникновения увеличивает прочность связи внешних электронов с ядром. Поэтому, если у d-элементов 4
периода 4s-электроны попадают под экран 3d-электронов, то у dэлементов 6 периода 6s-электроны попадают под двойной экран 5d- и 4fэлектронов. Отсюда при переходе от 4 к 6 периоду прочность связи
внешних s-электронов с ядром повышается, а потому и потенциал ионизации возрастает.
Сродство к электрону
Количество энергии Е, которое выделяется или поглощается
при присоединении электронов к нейтральному атому с превращением его в отрицательный ион, называется сродством к электрону
Э0 + е → Э + Е.
Размерность [E] = кДж/моль или эВ/атом.
Надежные значения сродства к электрону атомов найдены лишь для
небольшого числа элементов (72). Имеющиеся данные, однако, показывают, что в периодах и группах сродство к электрону атомов изменяется
закономерно в соответствии с характером электронных структур атомов
элементов. Наибольшим сродством к электрону обладают р-элементы 7
группы. Наименьшее или даже отрицательное сродство к электрону
имеют атомы с конфигурацией s2 (Be, Mg, Zn) и s2p6 (Ne, Ar, Kr) или с
наполовину заполненным р-слоем (N, P, As). Это служит дополнительным доказательством устойчивости указанных конфигураций.
Наибольшее сродство к электрону имеют галогены:
F – 3.45 эВ,
Cl – 3.61 эВ,
Br – 3.36 эВ,
I – 3.06 эВ.
Щелочные металлы имеют небольшое сродство к электрону:
Li – 0.54 эВ,
Na – 0.74 эВ.
Бериллий, магний, азот и инертные газы имеют даже отрицательные величины энергий сродства к электрону:
220
Be (-0.6 эВ), Mg (-0.3 эВ), N (-0.2 эВ), He (-0.22 эВ), Ne (-0.22 эВ).
Для того, чтобы решить вопрос о том, легче или труднее атом теряет или принимает электрон, учитывают обе характеристики: энергию
ионизации и сродство к электрону. Величина, учитывающая способность атома присоединить или отдать электрон, называется электроотрицательностью. Часто под электроотрицательностью понимают способность атомов в молекуле притягивать электроны.
В 1930 г. Л. Полинг предложил характеризовать электроотрицательность величиной χ
χ = √∆Е,
где ∆Е = ЕАВ – 1/2 (ЕАА + ЕВВ),
где ЕАА, ЕВВ и ЕАВ – энергии связи между атомами А и В в молекулах
АА, ВВ, АВ.
Пример: Рассчитайте электроотрицательность брома по Полингу,
пользуясь тем, что ЭО атома водорода равна 2,20.
χА – χВ = 0.102 1/2
∆HBr:
∆ = ЕсвHBr – [ЕсвH2 ⋅ ЕсвBr2]1/2 = 362 – [432 ⋅ 190]1/2 =
= 362 – 286 = 76 кДж/моль
χBr – χH = 0.10002 ⋅ 761/2 = 0.102 ⋅ 8.7 = 0.89
χBr – χH = 0.89; χBr =χХ + 0.89 = 2.20 + 0.89 = 3.09
Полученное значение несколько отличается от табличного. Отличие
связано с тем, что в таблицах приводятся усреднённые значения многих
подобных расчетов.
Шкала электроотрицательности Полинга наиболее распространена.
По этой шкале самую высокую электроотрицательность имеет атом
фтора (4.0). Кроме шкалы электроотрицательностей Полинга, известна
шкала Малликена, согласно которой
χ = 1/2 (Еиониз + Еср).
Известна еще шкала электроотрицательности Олреда и Рохова, которые
рассчитали ее по формуле:
221
χ = 0.359z/r2 + 0.744,
где z – эффективный заряд ядра, который действует на внешний электрон; r – средний радиус орбитали (часто равен ковалентному радиусу
атома).
Электроотрицательность возрастает в каждом периоде и уменьшается в группах.
Li
1.0
Пример:
Be
1.5
B
2,0
Al
1.5
Ga
1.8
In
1.5
Tl
1.5
C
2.5
Si
1.9
Ge
2.02
Sn
1.96
Pb
2.33
N
3.1
O
3.5
F
4.1
Cl
2.9
Br
2.8
I
2.2
At
2.0
Но это уменьшение не монотонно. Как видно из приведённого примера, монотонность нарушается у элементов четвёртого и шестого периодов. Причиной нарушения является 3d- и 4f-сжатие.
Электроотрицательность – очень удобная характеристика атома. Её
широко используют в химии для оценки характера химической связи
между атомами. При разности электроотрицательностей взаимодействующих атомов более 2 образуется ионная связь. Если разность электроотрицательностей 0,4 -2,0, то образуется ковалентная связь с частично ионным вкладом. Если же разность электроотрицательностей меньше
0,4, то связь считается чисто ковалентной.
Орбитальные радиусы атомов и ионов
Согласно квантовой механике, электрон может находиться в любой
точке вокруг ядра атома. Поэтому границы атомов расплывчаты и неопределенны. В то же время квантовая механика позволяет произвести
расчет вероятности распределения электронов вокруг ядра и положение
максимумов электронной плотности для каждой из орбиталей атома.
Теоретически рассчитанное положение главного максимума электронной плотности отдельных орбиталей называется их орбитальным
222
радиусом. Радиус внешней орбитали атома или иона определяет атомный или ионный орбитальный радиус.
Электронная плотность в многоэлектронном атоме рассчитывается
на основе того или иного приближения квантовой механики. Поэтому
величина орбитального радиуса не является абсолютной. Но соотношения орбитальных радиусов правильно передают общие закономерности
электронного строения атомов, их зависимости от квантовых чисел или
заряда ядер.
Расчет орбитальных радиусов выявил ряд важных особенностей.
Так, среди ns-подуровней только 1s имеет один максимум. Остальные
ns-подуровни имеют ряд более мелких максимумов, располагающихся
ближе к ядру, то есть электроны этих подуровней не только могут проникать в более глубокие части атома, но и находиться там с большой
долей вероятности. Число добавочных внутренних максимумов на единицу меньше главного квантового числа n, соответствующего nsподуровню (у 2s – один дополнительный максимум, у 3s – два дополнительных максимума). Меньшей проникающей способностью обладают
p-электроны, затем d- и f-электроны. При этом первые подуровни этих
электронов 2p, 3d, 4f – обладают также единственным максимумом. А
последующие (например, 3p, 4d, 5f и т.д.) имеют по нескольку добавочных максимумов (n-1 – добавочный максимум).
Подуровни 1s, 2p, 3d, 4f называют кайносимметричными, а соответствующие электроны – кайносимметриками.
Термин "кайносимметрия" был введен в 1969 г. на Международном
юбилейном Менделеевском съезде. Слово "кайнос" – греческое, означает "новый", т.е. кайносимметрики являются новыми (первыми) среди
s,p,d,f-электронов соответственно. Термин предложен академиком С.А.
Щукаревым.
Величина атомного орбитального радиуса не всегда совпадает с орбитальным радиусом орбитали с максимальным значением l. Особенно
хорошо это видно на примере элементов от C до Ne.
2 s1/2
2 p1/2
2 p3/2
Li
1.586
Be
1.040
B
0.796
0.776
C
0.620
0.956
N
0.512
0.487
0.488
O
0.450
0.413
0.414
F
0.396
0.359
0.360
Ne
0.354
0.317
0.318
Атомные орбитальные радиусы для элементов, следующих за бором, отвечают главному максимуму не 2p-, а 2s-электронов. Это связано
223
с тем, что главный максимум электронной плотности кайносимметриков
может быть ближе к ядру, чем у орбиталей с тем же значением n и l,
меньшим на единицу. Поэтому главные максимумы 3d-орбиталей, от Mn
и до Kr, также оказываются меньше главных максимумов 3p-орбиталей
тех же атомов. Аналогично и у 4f-электронов. Для остальных атомов
величина атомного орбитального радиуса совпадает с орбитальным радиусом орбитали.
3 s1/2
3 p1/2
3 p3/2
Na
0.713
Mg
1.279
Al
1.044
1.312
Si
0.904
1.068
P
S
Cl
Ar
0.916
0.919
0.806
0.810
0.722
0.725
0.655
0.659
Анализ изменения атомных орбитальных радиусов показывает:
1. Величины орбитальных радиусов (rорб) являются прерывистой
функцией z: в каждом периоде они уменьшаются с ростом z;
2. На фоне главной периодичности, начиная с элементов 3 периода, выявляется внутренняя периодичность – своя для s-,p-,d- и fэлементов соответственно (в общем уменьшается);
3. На фоне внутренней периодичности для d и f-элементов наблюдается вторичная периодичность в изменении rорб вследствие заполнения
d- и f-орбиталей по одному или по два электрона.
По группам сверху вниз радиусы растут, но этот рост не монотонный.
Al
Ga
In
Tl
rорб,°А
1.312
1.254
1.382
1.319
Si
Ge
Sn
Pb
rорб,°А
1.068
1.090
1.240
1.215
Так, у Ga наблюдается даже уменьшение rорб по сравнению с Al.
Аналогично у Tl по сравнению с In и у Pb по сравнению с Sn. Это объясняется тем, что Ga находится за 3d-элементами, у которых заполняется 3d-подуровень (предвнешний подуровень – 3d – кайносимметрик –
имеет один главный максимум и сильнее взаимодействует с ядром, а это
приводит к d-сжатию оболочки электронов, и rорб уменьшается). Еще
сильнее проявляется f-сжатие или лантанидное сжатие.
224
Как уже указывали выше, орбитальные радиусы – это величины
расчетные. В действительности же мы имеем дело с реальными веществами, в которых атомы имеют определенные размеры. В реальной химии очень часто используется понятие «атомный радиус», который делится на металлический, атомный, ковалентный. Часто используется
понятие ионный радиус.
Эти величины являются условными. Они вычисляются из межатомных расстояний, которые зависят не только от природы атомов, но и от
типа химической связи и от агрегатного состояния вещества.
При рассмотрении простых веществ, а также органических соединений говорят об атомных радиусах rат. При изучении ионных соединений чаще говорят об ионных радиусах.
Атомные радиусы делятся на радиусы металлов и ковалентные радиусы неметаллов. Металлические радиусы получены делением пополам расстояния между центрами любых двух смежных атомов в кристаллической решетке металла.
По периоду атомные радиусы металлов уменьшаются:
rат,Na = 1.89 °A;
rат,Mg = 1.60 °A; rат,Al = 1.43 °А.
Медленно уменьшается rат у d-металлов:
rат,Sc = 1.64°A;
rат,Co = 1.25°A;
rат,Ti = 1.46°A;
rат,Ni = 1.24°A.
rат,Fe = 1.26°A;
Еще меньше изменяются rат у лантанидов от 1.83 °А у Ce до 1.74 °А
у Lu. В главных подгруппах атомные радиусы растут сверху вниз, в побочных подгруппах тоже растут, но вследствие f-сжатия у элементов,
стоящих после лантанидов, радиусы близки:
Ti
Zr
Hf
1.46
1.60
1.59
rат, °A
V
Nb
Ta
rат, °A
4.34
1.45
1.46
Радиусы ионов
225
Если кристалл состоит из ионов, то межъядерное расстояние рассматривается как сумма ионных радиусов. Для ионных радиусов характерны следующие закономерности:
1. Для одинаковозарядных ионов со сходным электронным строением
радиус растет с увеличением числа электронных слоев.
Li+
rион,°А
0.68
Na+
0.97
K+
1.33
Cs+
1.67
2. Для ионов с одинаковым числом электронов rион уменьшается с ростом заряда.
S2rион, °А
1.74
K+
Cl
1.81
1.33
Ca2+
0.99
Положительный ион сильнее притягивает электроны, а в отрицательных ионах они отталкиваются.
3. Ионы с s2p6 оболочкой имеют радиусы больше, чем с d – оболочкой (d-сжатие).
Перспективы развития периодической системы
В связи с синтезом сверхтяжелых элементов перед теоретиками и
экспериментаторами возникает вопрос: где конец периодической системы? Может ли быть завершен VII период (до Z=118), могут ли быть получены элементы VIII периода, будет ли успешным синтез новых сверхтяжелых элементов? Систему атомных ядер Сиборг и Свяжецкий
аллегорически изобразили следующим образом. В море неустойчивости
находится материк стабильности (совокупность атомных ядер элементов
периодической системы, имеющих стабильные изотопы). На материке
стабильности, а также в окружающем его море неустойчивости есть
центры повышенной стабильности атомных ядер.
Как правило, ядра повышенной устойчивости характеризуются "магическим" числом протонов или нейтронов. Особенно устойчивы "дважды магические элементы", у которых и число протонов, и число нейтронов в ядре магическое, т.е. выражается числами 2, 8, 20, 50, 82, 114,
126, 164. Удивительно, что многие элементы с числом протонов, отвечающим магическим числам, попадают в IV группу периодической системы, хотя нет прямой связи между зарядом ядра и стабильностью ядер.
Не исключено, что после впадины неустойчивости, которая следует за
226
элементами №104, №105, №106, отличающимися крайне низкой стабильностью, последует остров стабильности, на котором будут находиться ядра с так называемыми замкнутыми протонными и нейтронными оболочками (это как раз те ядра, количество протонов и нейтронов в
которых соответствует магическим числам или близко к ним).
В частности, Сиборг предсказывает высокую стабильность элементов с Z = 110 и № = 184 (294110Э) и элемента экасвинца №114 с Z = 114 и
№ =200 (314114Э). Флеров также говорит о том, что есть надежда на синтез нуклидов, расположенных вблизи ядер с замкнутыми нуклонными
оболочками. В качестве примера он приводит ядра с нейтронной оболочкой, где число нейтронов равно 152. Изотопы с таким числом нейтронов особенно устойчивы для элементов №96 – №102. Именно благодаря стабилизирующему действию этой подоболочки, период
полураспада некоторых изотопов элемента №102 оказался достаточно
большим – порядка одной минуты.
Высказывая предположение о том, что элемент №114 будет обладать свойствами экасвинца, Сиборг полагал, что VII период после завершения ряда актинидов (№90 – №103) будет заполнен трансактинидами – 6d- и 7p-элементами (от №104 – экагафния до №118 – аналога
радона). Далее, в VIII периоде после аналогов щелочных и щелочноземельных элементов (№119, №120) и экаактиния (№121) будут следовать
f- и g-элементы, так называемые суперактиниды (№122 – 153). За ними
опять должны располагаться d- и p-элементы (№154 – 168), причем
№168 – инертный газ.
Следует отметить, что предсказание свойств элементов №114 (экасвинца), №113 (экагаллия) и других, находящихся вблизи острова стабильности, Сиборг основывает на закономерностях, вытекающих из периодического закона. Например, он полагает, что элемент №114 должен
быть преимущественно двухвалентным в своих соединениях, так как в
подгруппе германия, сверхтяжелым аналогом которого, вероятно, этот
элемент является, наблюдается тенденция к понижению степени окисления от (IV) до (II) при переходе от легких аналогов к тяжелым. При этом
Сиборг ссылается на термодинамические расчеты, согласно которым от
Ge к Pb уменьшается прочность ковалентной связи, и более вероятным
оказывается не sp3-гибридное состояние валентных электронов, а pсостояние.
Перспективы синтеза сверхтяжелых элементов, проверка предположений об относительной стабильности ряда изотопов некоторых элементов требуют разработки новых методов ядерного синтеза. При полу227
чении тяжелых актинидов и трансактинидов (искусственных элементов
VII периода) Сиборг и Гиорсо с сотрудниками пользовались облучением
нейтронами более легких ядер, чем получаемые. При этом заряд новых
ядер увеличивался на один нуклон (реакция многократного захвата нейтронов в интенсивных нейтронных потоках реакторов и ядерных взрывов). Флеров с сотрудниками для тех же целей использовали метод бомбардировки атомных ядер ускоренными ядрами неона. При такой
бомбардировке заряд ядра увеличивался сразу на несколько единиц.
Применяя разные методы синтеза сверхтяжелых ядер, советские и американские физики неизбежно получали разные изотопы сверхтяжелых
элементов. Кроме того, они использовали неодинаковые методы идентификации полученных элементов. Это одна из причин длительных споров о приоритете в открытии новых элементов.
Оба способа имеют свои достоинства и недостатки, но совершенно
очевидно, что оба они непригодны для синтеза элементов, следующих за
впадиной неустойчивости и расположенных на предполагаемом острове
стабильности. В самом деле, для синтеза, например, элемента №114 надо было бы по методике, использовавшейся ранее, иметь для облучения
легкими нуклонами (самый тяжелый из них – ядро неона) некоторое
количество атомов более легких предшественников элемента №114, но
эти элементы как раз попадают во впадину неустойчивости и не могут
быть синтезированы. Очевидно, что получить сверхтяжелые атомные
ядра можно лишь методами, исключающими необходимость предварительного получения нестабильных ядер. Такими методами, согласно
Флерову, могут быть следующие:
1. Синтез элемента №114 бомбардировкой актинидов потоком тяжелых ионов (Ar и Са). Недостаток этого метода состоит в том, что при
синтезе получаются нейтронодефицитные ядра с количеством нейтронов, далеким от магического числа N=184.
2. Уменьшение нейтронного дефицита достигается, например, при
бомбардировке плутония ядрами цинка:
94Pu
+ 80Zn → 124Э.
Число нейтронов в ядре элемента №124, получающемся таким образом, приближается к магическому N = 184. Однако ясно, что ускорить
ядра 30Zn до больших энергий – трудная задача.
3. Синтез элемента №114 (и его соседей по периодической системе)
бомбардировкой нейтроноизбыточных продуктов деления ускоренными
ионами ксенона. Важно, что при делении ядер актинидов образуются
228
изотопы, сильно обогащенные нейтронами (по сравнению с естественными изотопами тех же элементов). Так, облучение урана ксеноном, как
полагает Флеров, приведет к синтезу достаточно стабильных, недефицитных по нейтронам изотопов элементов с Z = 114 – 126 и № ≈ 184.
Достижение центра "острова стабильности" возможно только с использованием тяжелых ядер:
232
82
307
90Th + 34Se →
123Э + p + 6n,
238
80
311
92U + 36Kr →
127Э + p + 6n.
Перспективна также бомбардировка урана ураном или урана ксеноном.
Последние успехи ядерного синтеза связаны с получением элементов №107 – №110. В 1984 г. в Дубне на новом мощном циклотроне V400 с использованием ядерных реакций типа:
Pb + Fe → 108Э, Bi + Mn → 108Э
были получены три изотопа элемента №108. Они были зафиксированы
по характерному для них α-излучению (44 акта распада). Авторы открытия считают, что обнаруженные изотопы элемента с Z = 108 значительно более стабильны к спонтанному делению, чем элементы №104 и
№106, что дает надежду на получение еще более стабильных элементов
при увеличении Z. Действительно, синтез элемента №110 показал, что
период полураспада, полученного бомбардировкой тория и урана ядрами Ca и Ar, изотопа элемента №110 составляет сотые доли секунды. Это
говорит о значительно большей стабильности элемента №110, чем, например, элемента №108, для которого период полураспада выделенного
изотопа составлял только 2 мс. Синтез элемента №110 вселил в авторов
этого исследования оптимизм – они считают, что уже нащупывается
"почва острова стабильности".
Синтез новых сверхтяжелых элементов, достижение "острова стабильности" и, по крайней мере, экспериментальная проверка упомянутых гипотез сдерживаются сейчас отсутствием чрезвычайно мощных
ускорителей тяжелых ионов. Однако существует способ проверки существующих гипотез. Он связан с поиском сверхтяжелых элементов в природе. Действительно, можно предположить, что некоторые изотопы
элементов, находящихся в районе "острова стабильности", достаточно
устойчивы к спонтанному распаду и поэтому могут быть обнаружены на
229
Земле и в Космосе. Например, по расчетам Сиборга, ядро элемента
№114 с дважды магическим числом нуклонов (Z = 114, N = 184) должно
иметь период спонтанного полураспада, равный 1016 лет, а период полураспада, сопровождающегося α-излучением, равный ∼1 году (β-распад
не предполагается).
Резко повысился интерес к поискам элемента №114 в природных
объектах после того, как Фаулер (США) в 1967 г. в следах космических
лучей на эмульсиях обнаружил треки, которые могли оставить элементы
с зарядом ядра Z = 103 – 110. С этого времени поиски сверхтяжелых
элементов ведутся во всем мире.
Можно предположить, что в земной коре имеется долгоживущий,
спонтанно делящийся излучатель. Следы его деления наблюдались в
некоторых образцах свинцовых стекол. Следы деления нельзя приписать
обычному свинцу, но они могут принадлежать его тяжелому аналогу.
Если период полураспада экасвинца больше, чем 108 лет, то содержание
его в образцах достаточно для обнаружения. Для этих целей используется чрезвычайно чувствительная аппаратура – так называемые пропорциональные счетчики, в которых фон, определяемый космическим излучением, сведен к минимуму – 1 импульс за 30 суток. В таких условиях
фиксируемые акты распада предполагаемого экасвинца составляют 85 –
90% от общей фиксируемой активности.
Надо отметить, однако, что не все исследователи согласны с тем,
что обнаруженный спонтанный распад принадлежит экасвинцу. С их
точки зрения период полураспада обнаруженного элемента слишком
мал для того, чтобы данный изотоп до нашего времени мог сохраниться.
Не исключено, что ошибка состоит как раз не в самом факте обнаружения, а в определении периода полураспада. Так или иначе поиски сверхтяжелых элементов в природе (космическая пыль в снегах Арктики,
свинцовые руды, метеориты и т.д.) продолжаются.
Контрольные вопросы
1. В чем суть принципа Паули, и как он позволяет строить электронные конфигурации различных атомов?
2. Какую роль в построении электронных оболочек играет правило
Хунда? Каков физический смысл правила Хунда?
3. Что представляет собой экранирование электронов в атоме?
230
4. Почему первый потенциал ионизации у кислорода меньше, чем у
азота?
5. Почему химические свойства переходных элементов изменяются
в меньшей степени, чем свойства непереходных элементов?
6. Какие ионы называют изоэлектронными?
7. Как можно объяснить уменьшение радиусов ионов в ряду As3-,
Se2-, Br , Rb+, Sr2+, Y3+?
8. Каким образом электроотрицательность связана с первой энергией ионизации и энергией сродства к электрону?
9. Почему второй потенциал ионизации атома бериллия больше, чем
первый, но тем не менее значительно меньше второго потенциала
ионизации атома лития?
10. Объясните, почему сродство к электрону у атомов кремния и серы больше, чем у фосфора?
11. Какой физический смысл имеет атомный номер элемента, и почему химические свойства атомов, в конечном счете, определяются зарядом ядра элемента?
12. Для каких d-элементов число валентных электронов и максимальная степень окисления совпадает с номером группы?
13. На основании положения элементов в периодической системе
сделайте вывод, какой ион имеет максимальный радиус: Se2-, Br
, Rb+, Se2+?
14. Как зависит величина потенциала ионизации элемента от главного квантового числа?
15. Можно ли с уверенностью заявить о положении в периодической
системе элемента с порядковым числом более 30?
16. Каковы перспективы расширения границ периодической системы?
17. Чем можно объяснить аномалии в электронных структурах атомов хрома, меди?
18. Чем характеризуется распределение электронной плотности кайносимметричных электронных орбиталей?
19. Почему атомный радиус галлия меньше атомного радиуса алюминия?
20. Каким образом по значению разности электроотрицательностей
элементов в составе молекулы можно оценить тип химической
связи?
Задачи
231
1. Вычислите электроотрицательность водорода, исходя из того,
что ЭО фтора равна 3,98. Необходимые энергии связей найдите в
справочнике.
2. Вычислите электроотрицательность атома хлора, учитывая, что
ЭО атома водорода равна 2,20. Необходимые данные найдите в справочнике.
3. При нормальных условиях только 11 элементов периодической
системы в свободном состоянии являются газами и 2 элемента в свободном состоянии – жидкости. Укажите символы и названия этих элементов. Верно ли утверждение, что в тех же условиях существует 11 газообразных простых веществ? Может ли их быть больше? Для какого
простого вещества жидкое агрегатное состояние является необычным?
Почему?
4. Предположим, что в какой-то другой Вселенной обнаружено вещество, состоящее из атомов, "электроны" которых подчиняются следующим ограничениям на квантовые числа:
n>0
l = 0,1,2....(n-1)
m = +1 или -1
S = +1/2
Какие порядковые номера имеют в такой Вселенной первые два
инертных газа, учитывая, что к этим атомам применимы обычные правила заполнения электронных орбиталей?
5. В основном состоянии атом хрома имеет электронную конфигурацию 1s22s22p63s23p63d54s1. Предскажите электронную конфигурацию
первого возбужденного состояния атома хрома.
Дополнительная литература
1. Карапетьянц М.Х., Дракин С.И. Строение вещества. М.: Высш.
школа, 1978. С. 5-78.
2. Угай Я.А. Общая химия. М.: Высш. школа, 1977. С. 30-70.
3. Новиков Г.И. Основы общей химии. М.: Высш. школа, 1988. С.
158-233.
232
4. Дикерсон Р., Грей Г., Хейт Дж. Основные законы химии. Т. 1. М.:
Мир. 1982. С. 302-414.
5. Мартыненко Л.И., Спицын В.И. Методические аспекты неорганической химии. М.: Изд-во МГУ, 1983. С. 4-18.
6. Мартыненко Л.И., Спицын В.И. Неорганическая химия. Ч. 1. М.:
Изд-во МГУ, 1991. С. 338-377.
7. Дмитриев И.С. Электрон глазами химика. Л.: Химия. 1986. С. 5103.
8. Павлов Н.Н. Теоретические основы общей химии. М.: Высш.
школа. 1973. С. 22-49.
9. Новиков Г.И. Основы общей химии. М.: Высшая школа. 1988. С.
188-233.
233