Рассчитать термодинамические параметры реакции CCl O ↔ CO + Cl
реклама
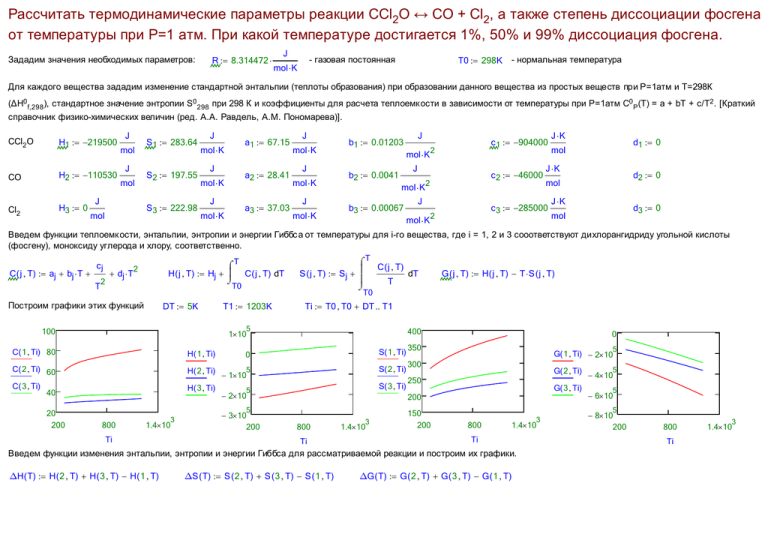
Рассчитать термодинамические параметры реакции CCl2O ↔ CO + Cl2, а также степень диссоциации фосгена от температуры при P=1 атм. При какой температуре достигается 1%, 50% и 99% диссоциация фосгена. Зададим значения необходимых параметров: R 8.314472 J - газовая постоянная mol K T0 298K - нормальная температура Для каждого вещества зададим изменение стандартной энтальпии (теплоты образования) при образовании данного вещества из простых веществ при P=1атм и T=298К (∆H0 f,298 ), стандартное значение энтропии S0 298 при 298 К и коэффициенты для расчета теплоемк ости в зависимости от температуры при P=1атм C0 P(T) = a + bT + c/T2 . [Краткий справочник физико-химических величин (ред. А.А. Равдель, А.М. Пономарева)]. CCl2 O H1 219500 CO H2 110530 Cl2 H3 0 J mol J mol J S1 283.64 S2 197.55 S3 222.98 mol J a1 67.15 mol K J a2 28.41 mol K J a3 37.03 mol K J mol K J mol K J mol K b1 0.01203 b2 0.0041 J mol K c 1 904000 2 J mol K b3 0.00067 c 2 46000 2 J mol K d1 0 mol J K d2 0 mol c 3 285000 2 J K J K d3 0 mol Введем функции теплоемк ости, энтальпии, энтропии и энергии Гиббс а от температуры для i-го вещества, где i = 1, 2 и 3 сооответствуют дихлорангидриду угольной кислоты (фосгену), моноксиду углерода и хлору, соответственно. C ( j T) aj bj T cj T 2 dj T T H ( j T) Hj C ( j T) dT 2 T0 Построим графики этих функций DT 5K Ti T0 T0 DT T1 400 1 10 C ( 1 Ti) 80 H ( 1 Ti) C ( 2 Ti) 60 H ( 2 Ti) 1 105 C ( 3 Ti) H ( 3 Ti) 40 5 2 10 800 1.4 10 Ti 3 10 200 0 S( 1 Ti) 350 300 S( 2 Ti) 250 S( 3 Ti) 200 0 5 3 G ( j T) H ( j T) T S ( j T) T0 T1 1203K 5 100 20 200 T C ( j T) dT S ( j T) Sj T 800 Ti 3 1.4 10 150 200 5 G( 1 Ti) 2 10 G( 2 Ti) 4 105 G( 3 Ti) 5 800 ΔS ( T) S ( 2 T) S ( 3 T) S ( 1 T) 3 1.4 10 Ti Введем функции изменения энтальпии, энтропии и энергии Гиббса для рассматриваемой реакции и построим их графики. ΔH ( T) H ( 2 T) H ( 3 T) H ( 1 T) 5 6 10 ΔG ( T) G ( 2 T) G ( 3 T) G ( 1 T) 8 10 200 800 Ti 3 1.4 10 5 2 10 ΔH( Ti) 5 1 10 Ti ΔS( Ti) ΔG( Ti) 0 0 5 1 10 5 2 10 200 3 3 1 10 600 1.4 10 Ti Обозначим за α степень превращения (диссоциации) фосгена. Тогда исходные и равновесные количества молей веществ равны следующим значениям + Cl2 Σ Вещество CCl2 O <-> CO исходное кол-во молей 1 0 0 1 равновесное кол-во молей 1-α α α 1+α Равновесные парциальные давления равны общему давлению, умноженному на равновес ные молярные доли + Cl2 Σ Вещество CCl2 O <-> CO Давление (1-α)/(1+α)P α/(1+α)P α/(1+α)P P PCOPCl2 Согласно закону действующих масс: PCCl2O ⋅ atm = KP (T ) = e - a a 2 a P P a a 1 + 1 + KP (T ) = = 1- a atm 1 - a2 atm 1+ a DG (T ) RT Это уравнение можно решить относительно α аналитически 2 Given α K P ( T) = 2 Find ( α) 1 α KP ( T) KP ( T) 1 KP ( T) KP ( T) 1 K P ( T) 1 K P ( T) 1 Задав функции константы равновесия и степени превращения (предварительно немного упростив, полученное выражение для α), построим их графики ΔG ( T) RT KP ( T) exp α ( T) K P ( T) K P ( T) 1 3 1 1 0.8 1 10 ΔG( Ti) R Ti exp 1 3 1 10 α( Ti) 6 1 10 9 1000K 0.6 0.4 0.2 1 10 12 1 10 200 500K 3 1 10 600 Ti 3 1.4 10 0 200 3 1 10 600 Ti 3 1.4 10 Видно, что при Т ~> 500К степень диссоциации фосгена становится более 1%, а при Т ~> 1000К - более 99%. В данной задаче нам удалось получить аналитическое выражение для α(T). Однако зачастую это сделать невозможно. Покажем, как можно рас считать α(T) численно и сравним расчетные значения с точными. αn .5 - начальное значение α с которого Mathcad начинает численный поиск решения уравнения Given 2 K P ( T) = αn 2 1 αn αnum( T) Find ( αn) 15 1 10 αnum( Ti) α( Ti) 0 15 1 10 200 3 1 10 600 3 1.4 10 Ti В заключение определим при какой температуре достигается 1%, 50% и 99% диссоциация фосгена. Приблизительные значения (с точностью DT 5 K ) можно найти, используя контек стное меню "Trace...", построенного выше графика α(T). Получить точное значение температуры, при к оторой достигается некоторая степень диссоциации можно так: T 1200K Given 2 K P ( T) = α 2 1 α Tnum ( α) Find ( T) Tnum ( 1 % ) 510.4039 K Tnum ( 50 % ) 748.0909 K Tnum ( 99 % ) 1055.4815 K




