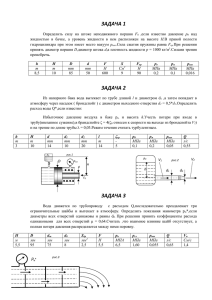
Профилирование боковой поверхности поршней ДВС

Конструкция ДВС
УДК 621.436-242-713.2.001.5
Ф.И. Абрамчук, д-р техн. наук, С.А. Кочетов, асп.
ПРОФИЛИРОВАНИЕ БОКОВОЙ ПОВЕРХНОСТИ ПОРШНЕЙ ДВС
К поршням современных ДВС постоянно повышаются требования по долговечности. Одной из
составляющих этого критерия является надежная
работа поршня и гильзы цилиндра как пары трения,
которая в большей мере определяется геометрией
контактируемых поверхностей.
В настоящее время, на фирмах – производителях поршней, задача профилирования боковой поверхности поршня (БПП) решается при проектировании новых конструкций и при усовершенствовании имеющихся. При этом преследуется основная
цель – исключение задира поршня на всех режимах
работы ДВС.
Распространенным методом нахождения оптимального профиля БПП является его экспериментальная доводка на стенде и на “развернутых” двигателях. Но получаемый, таким образом, положительный результат не решает важной теоретической задачи – определение взаимосвязи формы БПП с форсировкой двигателя. Как следствие, невозможно рассчитать профиль на стадии технического проекта и
более
эффективно
прогнозировать
техникоэкономические показатели ДВС. Поэтому новые методы получения профиля БПП полностью востребованы.
Один из общих методов профилирования
поршня предложен в работе [1]. Он базируется на
решении задачи теплопроводности вдоль юбки
поршня, которое имеет вид:
ch K m 1   
t  tг 
 tв  tг  ,
ch K m
где  
t t
z
L
, Km 
 arch в п ,
L
t
 м s /  м
н  tп
t – температура юбки поршня, tг – средняя
температура гильзы, tв – температура юбки поршня в
верхней части, tн – температура юбки поршня в
нижней части, L – длина юбки, z – текущая координата по оси поршня от верхней части юбки, м –
толщина масляной пленки, s – толщина стенки юбки,
 - коэффициент теплопроводности материала юбки,
м - коэффициент теплопроводности масляной пленки.
Наиболее точное, по мнению авторов, значение Кт дает разность температур, которая и является
основным параметром при профилировании. Но
температура юбки поршня не отслеживает его динамику деформации за рабочий ход, которая влияет на
изменение площади контакта с цилиндром и определяет удельное давление на БПП.
46
Поэтому предлагается метод, в котором формы БПП взаимосвязаны с деформацией поршня под
действием температуры и газовых сил, что позволяет
проводить оптимизацию форм БПП при заданной
форсировке ДВС.
Метод апробировался на поршнях тепловозных дизелей ЧН 26/27 производства ГП “Завод имени Малышева” и, в частности, на составном поршне
(стальная головка + чугунная юбка) (рис.1).
Рис. 1. Чугунная юбка составного поршня
Допустим, что указанная конструкция поршня
существует только на уровне технического проекта.
На рис.2 показано положение поршня в цилиндре. Площадь контакта s определяется пересечением эквидистанты поверхности цилиндра с поверхностью поршня. При этом s зависит от эффективной
толщины масляной пленки эф и характеризуется
геометрическими параметрами yм и zм . Решение задачи деформированного состояния методом конечных элементов при заданных, в первом приближении, силовых и температурных граничных условиях.
Оперативно и с допустимой точностью позволяют рассчитать трехмерную модель такие программные продукты, как ANSYS, Design Space и т.д.
На этой стадии выявляется зависимость деформации
юбки поршня от давления в цилиндре и результирующей температуры. Для рассматриваемой конструкции верхняя часть юбки остается цилиндрической, а в нижней части овализируется на 40мкм при
давлении вспышки 14 МПа.
Решение контактной задачи в геометрической
постановке.
На данном этапе, форма БПП образуется эллиптическими линиями уровня, у которых малая и
большая оси определяются наклонами образующих
ДВИГАТЕЛИ ВНУТРЕННЕГО СГОРАНИЯ 12002
Конструкция ДВС
рабочей поверхности и холодильника при рабочем
ходе поршня (результаты предыдущего расчета).
где нижнее маслосъемное кольцо выполняет, в основном, маслораспределительную функцию.
Сила трения в области контакта будет характеризоваться осредненным коэффициентом трения f,
и его нахождение определяет экспериментальную
часть метода.
Испытания образцов материала рассматриваемого поршня осуществлялись на машине трения
СМТ–1 по схеме ролик – колодочка (рис.3). Ролик
изготовлен из чугуна, применяемого для изготовления гильз цилиндров, а колодочка - из материала
поршня. Процесс трения исследовался при условиях,
соответствующих всем участкам рабочего хода
поршня. Определено, что на большей его части значение f = 0,02  10%, т.е. соответствует условиям
граничного и полужидкостного трения. Так для принятого режима трения справедливо уравнение из
гидродинамической теории смазки:
s   v
,
 эф 
N  f эф
где N – нормальное усилие на рабочую БПП, 
– динамическая вязкость масла, v– скорость движения поршня.
Рис. 2. Положение поршня в цилиндре
Для нахождения эф необходимо определить
характер процесса трения. Он будет различен для
поршней с нижним маслосъемным кольцом и без
него, а также зависеть от состояния контактирующих
поверхностей.
Поверхность
рассматриваемого
поршня покрывается твердой смазкой ВАП (МоS2)
[2] толщиной 15…20 мкм. Перед покрытием поверхность поршня подвергается дробеструйной обработке с образованием шероховатости 20…25 мкм. Опыт
эксплуатации поршней с данным покрытием на тепловозных дизелях производства ГП “Завод имени
Малышева” и Коломенского завода (РФ) показывает,
что стабилизация процесса изнашивания наступает
при срабатываемости толщины покрытия на
50…60%. Учитывая вышесказанное, для поршней с
эффективным нижним маслосъемным кольцом будет
присутствовать только сухое и граничное трение, а
положение эквидистанты определится значением
эф=7…10мкм. Для поршней без нижнего маслосъемного кольца можно говорить о присутствии еще
и жидкостного трения на периферии области контакта. Это справедливо и для рассматриваемого случая,
ДВИГАТЕЛИ ВНУТРЕННЕГО СГОРАНИЯ 12002
Рис. 3. Схема испытания образца поршня
Принимая во внимание отношение коэффициентов трения при жидкостном и полужидкостном
трении равное, 7…10 запишем следующее эмпирическое уравнение для эф
f / fэф = (7…10)
s   v  (7...10)
'
 эф 
  эф
(1)
Nf
В первом приближении, для решения предлагается использовать именно равенство (1).
При движении поршня по гильзе, угол его наклона определяется из условия равенства момента
силы трения относительно оси поршневого пальца и
момента боковой силы N относительно “центра тяжести” площади контакта поршня и гильзы (рис.2).
47
Конструкция ДВС
N (zп –zс) = 0,5 D f ,
(2)
где D – диаметр поршня.
Таким образом, совместное решение уравнений (1) и (2) позволяет получить ряд зависимостей
для выбора формы БПП. Для рассматриваемой конструкции они представлены на рис.4 – 6. Так, радиус
кривизны профиля рабочей поверхности поршня
R=100000 мм обеспечивает допустимое максимальное давление 4,37 МПа. Угол наклона хорды  =
0,02 (положительный угол смещает максимальный
диаметр поршня ниже оси поршневого пальца, а отрицательный – выше оси) обеспечивает равномерную эпюру распределения давления Р по БПП и приемлемое изменение угла наклона оси поршня к оси
цилиндра .
а)
Рис. 4. Зависимость максимального удельного
давления на рабочую БПП от радиуса кривизны
профиля
б)
в)
Рис. 5. Эпюры удельного давления на рабочую БПП при заданной кривизне профиля:
а) R=50000 мм; б) R = 100000 мм; в) R = 150000 мм
Рис. 6. Зависимость угла наклона оси поршня γ от угла поворота коленчатого вала α, при рабочем ходе поршня
48
ДВИГАТЕЛИ ВНУТРЕННЕГО СГОРАНИЯ 12002
Конструкция ДВС
Расчет, уточняющий профиль БПП.
По выбранному профилю поршня в горячем
состоянии находится профиль в холодном состоянии
по методике [1] и корректируется трехмерная модель. В контактной задаче уже оперируем не аппроксимированной эллиптическими функциями БПП, а
поверхностью поршня, заданной массивом точек,
полученным из расчета деформированного состояния конечно-элементной модели.
Таким образом, предложенный метод позволяет проанализировать варианты рабочей поверхности поршня, обеспечивающие заданную задиростойкость при определенных уровнях форсировки. Метод
остается “открытым” в плане использования уточ-
ненных эмпирических зависимостей для коэффициента трения. Все этапы расчета реализованы на базе
известных программных продуктов - Design Space и
MatCad, что делает предложенную выше методику
профилирования БПП доступной и удобной в использовании.
Список литературы:
1. Профилирование юбок поршней. Кол.авт.,
М., «Машиностроение», 1973, 88с. 2. Трение, изнашивание и смазка. Справочник. В 2-х кн. Кн.2. Под
ред. И.В. Крагельского и В. В. Алисина. – М.: Машиностроение, 1979. – 358с., ил.
УДК 621.436.052
Н.К. Рязанцев, д-р техн. наук, Ю.А. Анимов, канд. техн. наук, Г.И. Быбыч, инж.,
Л.И. Стремоухов, инж.
К ОПРЕДЕЛЕНИЮ ЗАПАСА УСТОЙЧИВОЙ РАБОТЫ ЦЕНТРОБЕЖНОГО
КОМПРЕССОРА НАДДУВА ТРАНСПОРТНОГО ДИЗЕЛЯ
Одним из основных требований, предъявляемых к компрессору системы наддува транспортного
дизеля, является обеспечение его устойчивой работы
на всех эксплуатационных режимах. Для сокращения
трудозатрат и времени на создание нового двигателя
анализ взаимного расположения расходной (гидравлической) характеристики дизеля и границы помпажа компрессора следует проводить на стадии проектирования. Такое аналитическое исследование можно провести с помощью следующей методики.
На рис. 1 на поле характеристик компрессора
 K  f (Gnp , U np ) изображена расходная характеристика дизеля (АВ) с крайними точками: (А) - режим
номинальной мощности (Nен ) и (В) - режим максимального крутящего момента (Мкр макс).
Для прогнозирования запаса устойчивости
компрессора на этих режимах внешней характеристики дизеля необходимо знать закон протекания
границы помпажа компрессора. На основе проведенного анализа характеристик большого количества
отечественных и зарубежных одноступенчатых центробежных компрессоров автором [1] показано, что в
большом диапазоне изменения окружной скорости
рабочего колеса U 2  0,7...1,0, присущем работе
компрессора с механической связью с дизелем, и,
тем более, при свободном турбокомпрессоре, относительное изменение расхода воздуха вдоль границы
неустойчивой работы определяется уравнением:
ДВИГАТЕЛИ ВНУТРЕННЕГО СГОРАНИЯ 12002
K 1

 0, 37   KK

K 1
 0, 37   KK
0

2,22
K 1

 KK  1

G пр 
. (1)
 
K 1
G np0
K

 K0  1

При определении запаса устойчивости обычно
применяют выражение [2]:
G np
Рис 1. К определению условий совместной работы
двигателя и компрессора
49