Использование закономерностей выгорания углей для описания

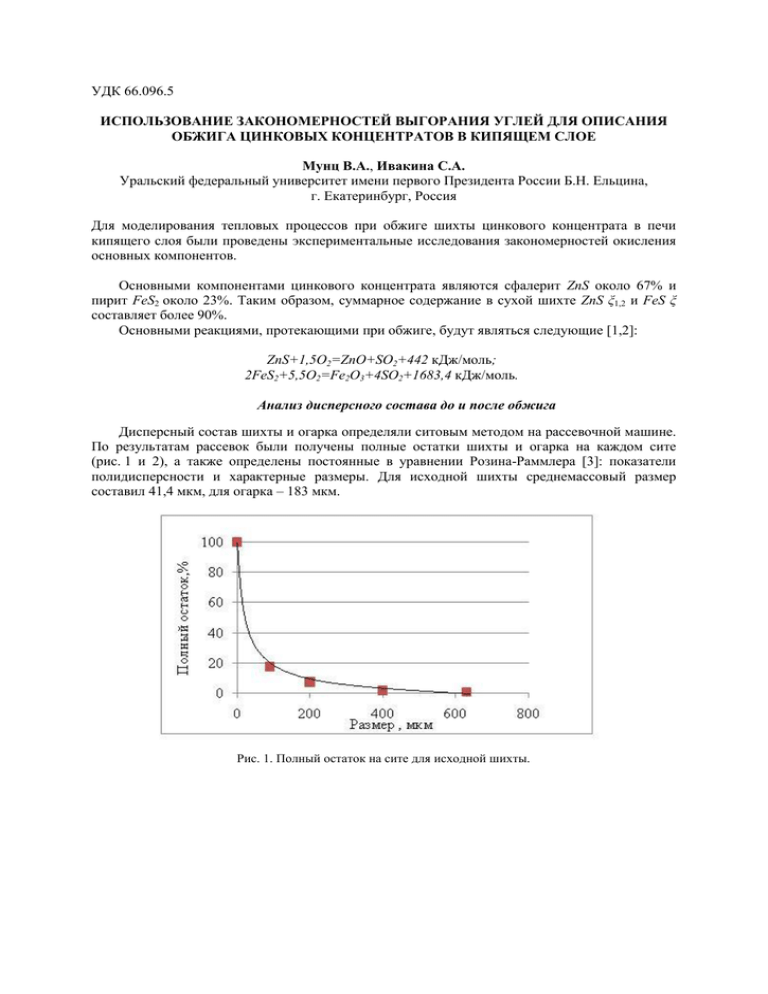
УДК 66.096.5
ИСПОЛЬЗОВАНИЕ ЗАКОНОМЕРНОСТЕЙ ВЫГОРАНИЯ УГЛЕЙ ДЛЯ ОПИСАНИЯ
ОБЖИГА ЦИНКОВЫХ КОНЦЕНТРАТОВ В КИПЯЩЕМ СЛОЕ
Мунц В.А., Ивакина С.А.
Уральский федеральный университет имени первого Президента России Б.Н. Ельцина,
г. Екатеринбург, Россия
Для моделирования тепловых процессов при обжиге шихты цинкового концентрата в печи
кипящего слоя были проведены экспериментальные исследования закономерностей окисления
основных компонентов.
Основными компонентами цинкового концентрата являются сфалерит ZnS около 67% и
пирит FeS2 около 23%. Таким образом, суммарное содержание в сухой шихте ZnS ξ1,2 и FeS ξ
составляет более 90%.
Основными реакциями, протекающими при обжиге, будут являться следующие [1,2]:
ZnS+1,5O2=ZnO+SO2+442 кДж/моль;
2FeS2+5,5O2=Fe2O3+4SO2+1683,4 кДж/моль.
Анализ дисперсного состава до и после обжига
Дисперсный состав шихты и огарка определяли ситовым методом на рассевочной машине.
По результатам рассевок были получены полные остатки шихты и огарка на каждом сите
(рис. 1 и 2), а также определены постоянные в уравнении Розина-Раммлера [3]: показатели
полидисперсности и характерные размеры. Для исходной шихты среднемассовый размер
составил 41,4 мкм, для огарка – 183 мкм.
Рис. 1. Полный остаток на сите для исходной шихты.
Рис. 2. Рассевка оставшихся в обжиговой печи фракций.
При известной скорости газов в печи кипящего слоя 0,83 м/с были рассчитаны диаметры
витания частиц δв для исходной шихты и огарка, которые составили соответственно 133 и
118 мкм [3]. Из рисунка 1 следует, что более 80% загружаемого концентрата имеет диаметр
меньше диаметра витания и частицы данных размеров будут вынесены из слоя.
Таким образом, укрупнение среднего размера частиц слоя (до 200 мкм) по сравнению с
исходным дисперсным составом шихты (41,4 мкм) обусловлено выносом мелких фракций.
Определение кинетических констант реагирования
Для изучения кинетики окисления цинкового концентрата (шихты) в кипящем слое были
проведены эксперименты на шихте и ее основных компонентах - сфалерите (ZnS = 67 %) и
пирите (FeS2 = 23,5 %).
Эксперименты выполнялись при различных температурах на приборе синхронного
термического анализа NETZSCH STA 449 F3, совмещенного с масс-спектрометрической
системой QMS 403C, предназначенной для качественного и количественного анализа
компонентов газовой смеси, выделяющейся в процессе термохимической конверсии.
В тигель помещали навеску массой m = 10 мг. Нагрев навески происходил в среде аргона,
при достижении требуемой температуры подавался воздух. Непрерывно измерялась масса
навески и относительная концентрация газовых компонентов.
В экспериментах использовали навески узких фракций: 0-200, 200-400, 400-630 мкм, при
этом средний размер частиц в навеске составлял: δ = 100, 300 и 515 мкм.
Обжиг навески сульфида цинка проводили при температурах 700, 800 и 900 оС в среде
воздуха, а также воздуха, обогащенного кислородом (О2 = 28%). Убыль массы навески
сфалерита в зависимости от времени при t = 900 оС представлена на рис. 3.
В период прогрева навески в среде аргона происходит незначительное уменьшение массы
за счет выхода влаги и реагирования сульфида цинка с кислородом, который находится в порах
вещества. При подаче воздуха происходит резкое, практически линейное, уменьшение массы
навески за счет протекания реакции окисления. В этот же момент масс-спектрометр фиксирует
образование SO2.
Как показали эксперименты, массовое количество сульфида цинка, реагирующего в
единицу времени, кг/с, не зависит от диаметра частиц в навеске, а зависит только от
температуры обжига. Это свидетельствует о протекании реакции во всем объеме частицы.
Фотографии (рис. 4) навесок сульфида цинка, шихты и пирита доказывают, что частицы имеют
развитую пористую поверхность как до, так и после обжига.
Рис. 3. Изменение массы навески сфалерита при t = 900 оС.
Рис. 4. Огарок цинкового концентрата.
Выражение для изменения массы реагирующего сульфида цинка в кг/с формально может
быть записано как
dm
  ZnS 

m0  d m m0
    K  C
(1)
O2 , кг/с.
d
d
Тогда, эффективная константа скорости химического реагирования может быть определена
по экспериментальным данным как:
 m  d  m / m0 
(2)
K  0
.

CO2  d
Здесь следует отметить, что размерность эффективной константы K м3/с, и фактически она
представляет собой произведение константы скорости химического реагирования на полную
поверхность реагирования S0 в м2. Коэффициенты, входящие в (1) представляют собой
коэффициент, учитывающий количество исходного вещества, вступившего в реакцию, к
 ZnS
97, 434
видимому изменению массы  

 6, 065 , и стехиометрический
 S  O
16
коэффициент реакции окисления сфалерита  
 ZnS
1, 5O
2

97, 434
1, 5  32
 2, 99.
Эксперименты показали, что значения эффективной константы скорости химического
реагирования в среде воздуха с концентрацией кислорода 21% и обогащенного кислородом до
28% практически совпадают. Это позволяет сделать вывод, что реакция ZnS  1,5O2 имеет
первый порядок по кислороду.
На рисунке 5 приведено сопоставление констант скорости реагирования сульфида цинка,
пирита и шихты. Константа скорости окисления пирита в 4 раза меньше константы скорости
окисления сфалерита. Пропорционально содержанию пирита в шихте уменьшается константа
скорости окисления шихты по сравнению со скоростью окисления сфалерита.
Рис. 5. Сопоставление констант скорости реагирования:
линии - расчет по аппроксимациям, точки – эксперимент.
Определение константы скорости химического реагирования
В экспериментах определена скорость химического реагирования сульфида цинка в виде
(1) и была получена эффективная константа скорости реагирования K, м3/с.
Пусть K  k  S 0 это произведение константы скорости реакции k в м/с на полную
поверхность реагирования S0 в м2. Если считать что поверхность реагирования
пропорциональна массе m0 = S0/ψ, то получим коэффициент пропорциональности ψ, имеющий
размерность м2/кг, т.е. это удельная поверхность в м2/кг. Тогда уравнение (1) может быть
записано в виде:
dm
d


m0 d m m0
d
   KC
O2   km0 CO2 , кг/с.
Удельная поверхность Si в м2/м3связана с глубиной проникновения ε соотношением
Si  1  . Если глубину проникновения принять равной радиусу наибольшей частицы (при
900 °С наблюдается падение K с увеличением диаметра), то при ε = 515/2 = 257,5 мкм или
ε = 2,575·10-6 м, а Si = 3883 м2/м3. При плотности сульфида цинка равной ρ = 4095 кг/м3
величина ψ = Si/ρ = 3883/4095 = 0,948 м2/кг. При плотности шихты 4360 кг/м3 величина
коэффициента ψ = Si/ρ = 3883/4360 = 0,89 м2/кг.
Оценим скорость химического реагирования, выраженную в м/с. Пусть при t = 950°C в
соответствии с экспериментальными данными для шихты K = 7·10-7 м3/с, тогда
k
K

7  10
7
 0, 0787 м/с. При концентрации кислорода при 950 °С равной
6
0,89  10  10
СО2 = 0,21·1,429·273/1223 = 0,067 кг/м3 поток кислорода к поверхности частицы за счет
 m0
протекания реакции равен j  k  CO  0, 0787  0, 067  0, 0053 кг/(м2с).
2
Коэффициент диффузии кислорода в азоте:
D  0,16  10
4 
1,9



 273 
T
 0,16  10
1,9
4  1223 



273 
 0, 276  10
3
м2/с.
Тогда коэффициент диффузионного массообмена равен:
d 
Sh  D
2  0, 255  10
3

 1, 07 м/с,
3

0, 515  10
т.е. коэффициент диффузионного массообмена на порядок выше константы скорости
химического реагирования.
Газообразование в кипящем слое при обжиге сульфида цинка
Пусть массовая концентрация частиц в слое сг имеет размерность кг/м3. Тогда
уравнение изменения концентрации кислорода по высоте слоя можно представить в виде:
dCO
  k mCO , кг/с.
2
dx
3
Здесь V – объём слоя, м ; m – масса частиц в объёме слоя. Разделив правую и левую часть на
объём слоя, получим:
Vw
w
2
dCO
2
  k CO c г , кг/(м3с),
2
dx
где сг = m/V – концентрация частиц сульфида цинка в объёме слоя. Начальная концентрация
кислорода на входе в слой равна С0 концентрации кислорода в дутье. В общем случае, она
больше 21%. Интегрируя от х = 0 до текущего значения, получим распределение концентрации
кислорода по высоте слоя в зависимости от концентрации сульфида цинка в объёме слоя сг:


CO  C0 exp  
2
k cг x 
 , кг/м3.

w
При конечной высоте слоя H концентрация кислорода на выходе из слоя будет равна:


C K  C0 exp  
k cг H
w

.

Данное выражение может быть преобразовано к следующему виду:


CK
 exp  
C0
k cг H
w



Коэффициент избытка воздуха связан с начальной и конечной концентрацией кислорода
следующим соотношением:
C
K 1 1  .


C  
0
(3)
Используя (3), получим выражение для определения коэффициента избытка воздуха на
выходе из слоя в зависимости от режимных параметров и высоты слоя Н:
1





 1  exp  
k cг H
w



(4)
Рис. 6. Расчетная зависимость коэффициента подачи окислителя от концентрации горючих веществ в
кипящем слое.
На рисунке 6 представлены результаты расчетов по выражению (4) при следующих
условиях: температура слоя 950 °С, высота слоя 1,6 м, скорость дутья 0,83 м/с, константа
скорости химического реагирования k = 0,074 м/с, коэффициент ψ = 0,89 м2/кг. По данным
микрорентгеновского анализа материала слоя содержание горючих веществ в нем составляет
1,5-3 %, а измеренный коэффициент подачи окислителя находится в диапазоне от 1,1 до 1,3.
Расход воздуха G, подаваемого на горение, может быть записан либо через скорость
воздуха u, приведенную к нормальным условиям, и площадь сечения топки F, либо через
величину теоретически необходимого количества V0 воздуха и его избыток [4]:
0
G  uF  BV .
Из данного равенства можно выразить расход топлива, выгорающего на 1 м2 сечения
топки, в зависимости от концентрации сульфида цинка в слое:
B

u
0

u
0




 1  exp  
k cг H

 , кг/(м2с).

F
V
V
w
На рисунке 7 представлена зависимость расхода выгорающего в обжиговой печи топлива
от средней концентрации горючих веществ в кипящем слое. Из расчетов следует, что расход
выгорающего топлива равен расходу подаваемого топлива при средней концентрации горючих
веществ в кипящем слое около 1%.
Рис. 7. Зависимость расхода выгорающей шихты от средней концентрации горючих веществ в
кипящем слое
Выводы:
1. Экспериментально определено, что реакция окисления сульфида цинка имеет первый
порядок по кислороду.
2. Экспериментально
определены
величины
энергии
активации
и
предэкспоненциальные множители реакций окисления сульфида цинка и пирита при
их окислении кислородом.
3. Экспериментально показано, что реакции окисления пирита и сульфида цинка
кислородом идет во внутрекинетиической области, когда реагирует весь объём
частицы.
4. Показано, что скорость окисления шихты уменьшается по сравнению со скоростью
окисления сфалерита пропорционально содержанию пирита в шихте.
5. Установлено, что укрупнение материала слоя по сравнению с исходной шихтой
обусловлено выносом мелких фракций, доля которых в шихте доходит до 80%.
6. Расчетами показано, что концентрация горючих веществ в кипящем слое в среднем
составляет около 2%, т.е. выгорание практически полное
Литература
1. Смирнов, Юрий Михайлович. Гидрометаллургия цинка: Учеб. пособие / Ленингр. горн.
ин-т им. Г.В. Плеханова .— Л. : ЛГИ, 1978 .— 95 с.
2. Термические константы веществ. /Под ред. В.П. Глушко, ВИНИТИ. -М.:, 1965-1981.
Вып. I-X.
3. Теория горения и топочные устройства. Под ред. Д.М. Хзмаляна. Учеб.пособие для
студентов высш. учеб. заведений. М., «Энергия», 1976.
4. Мунц В.А., Баскаков А.П., Ашихмин А.А. Расчет газообразования при горении твердого
топлива в кипящем слое. // ИФЖ, 1988, т. 54, № 3, с. 432-438.