t q x 

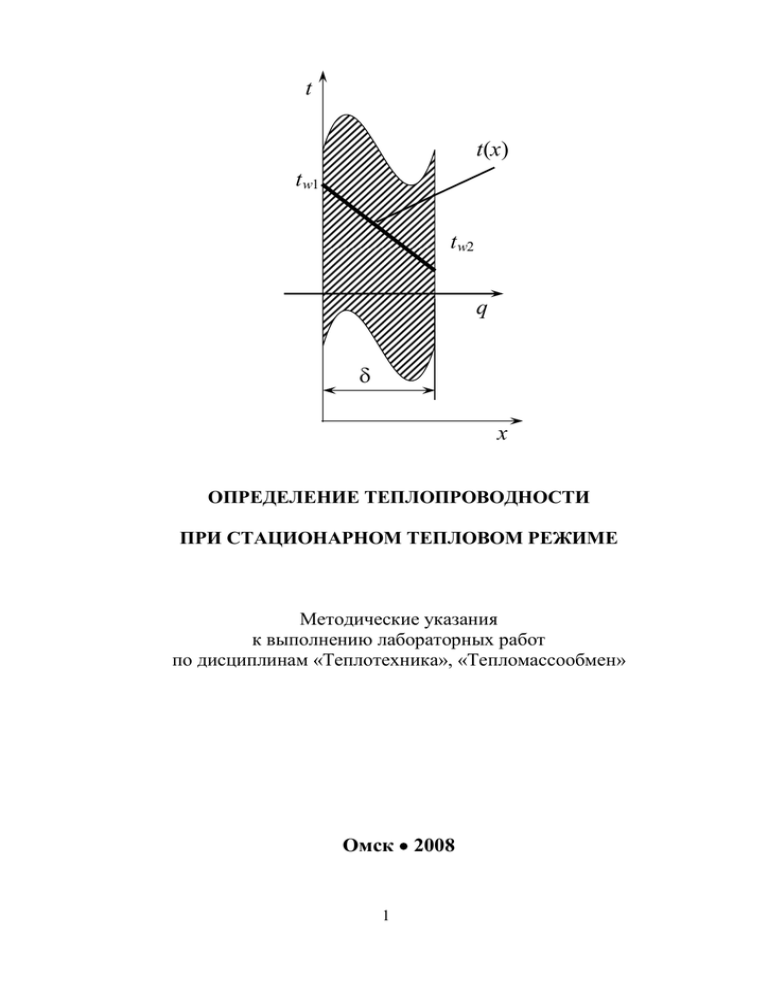
t
t(х)
tw1
tw2
q

x
ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ
ПРИ СТАЦИОНАРНОМ ТЕПЛОВОМ РЕЖИМЕ
Методические указания
к выполнению лабораторных работ
по дисциплинам «Теплотехника», «Тепломассообмен»
Омск  2008
1
Федеральное агентство по образованию РФ
Сибирская государственная автомобильно-дорожная академия
(СибАДИ)
Кафедра теплотехники и тепловых двигателей
ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ
ПРИ СТАЦИОНАРНОМ ТЕПЛОВОМ РЕЖИМЕ
Методические указания
к выполнению лабораторных работ
по дисциплинам «Теплотехника», «Тепломассообмен»
Составители: А.С.Ненишев, А.Л.Иванов
Омск
Издательство СибАДИ
2008
2
УДК 621.317.7
ББК 31.312
Рецензент д-р техн. наук, проф. В.И.Гриценко
Работа одобрена научно-методическими советами специальностей 190601,
190201, 270109, 190603, 190205 в качестве методических указаний по дисциплинам «Теплотехника» и «Тепломассообмен» для студентов очной и заочной форм
обучения.
Определение теплопроводности при стационарном тепловом режиме:
Методические указания к выполнению лабораторных работ по дисциплинам «Теплотехника», «Тепломассообмен» / Сост.: А.С.Ненишев., А.Л.Иванов.  Омск:
Изд-во СибАДИ, 2008.  32 с.
В методических указаниях изложены основы теории теплопроводности и
способы определения теплопроводности твёрдых материалов методами плоской и
цилиндрической стенок при стационарном тепловом режиме. Проводятся описание и порядок работы экспериментальной имитационной установки для определения теплопроводности в данном режиме, порядок проведения эксперимента в
диалоге с компьютером и методика обработки экспериментальных данных.
Табл. 7. Ил.8. Библиогр.: 5 назв.
 Составители: А.С.Ненишев,
А.Л.Иванов, 2008
3
ЛАБОРАТОРНАЯ РАБОТА № 1
ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛА
МЕТОДОМ ПЛОСКОЙ СТЕНКИ
1. Цели и задачи работы
Цели лабораторной работы: закрепление знаний по разделу
«Стационарная теплопроводность»; исследование процесса передачи
теплоты теплопроводностью через плоскую стенку при стационарном
тепловом режиме.
Задачи исследования:
 определить экспериментальным путём коэффициент теплопроводности испытуемого материала методом плоской стенки;
 установить факторы, влияющие на интенсивность передачи теплоты через плоскую стенку.
Оборудование и оснащение: имитационная экспериментальная установка по определению стационарной теплопроводности заданного
материала методом плоской стенки.
2. Теоретические основы
Согласно второму закону термодинамики самопроизвольный
процесс переноса теплоты происходит под действием разности температур и направлен от более горячего тела к более холодному, т.е. в
сторону уменьшения температуры.
Всего существует три вида передачи теплоты:
- теплопроводность;
- конвекция;
- тепловое излучение.
Теплопроводностью называется процесс передачи теплоты при
непосредственном контакте тел или частицами тел с различными температурами, который происходит на молекулярном уровне. Теплота
передается за счет переноса энергии микрочастицами из зоны с высокой температурой в зону с более низкой температурой в результате непосредственного контакта (межмолекулярных столкновений) микрочастиц с разным уровнем энергии.
Теплопроводность в основном имеет место в твердых телах и в незначительной степени присутствует в жидкостях и газах. Полностью
отсутствует в вакууме в силу отсутствия микрочастиц.
4
Таким образом, процесс передачи теплоты теплопроводностью сопровождается изменением температуры как в пространстве, так и во
времени.
2.1. Температурное поле
Аналитическое исследование теплопроводности сводится к изучению пространственно-временного изменения температуры, т.е. к нахождению уравнения
t  f ( x, y , z ,  ),
(1)
где t – температура; x, y, z – пространственные координаты;  − время.
Уравнение (1) представляет собой математическое выражение
температурного поля. Температурное поле есть совокупность значений температуры во всех точках изучаемого пространства для каждого
момента времени. Если соединить точки, имеющие одинаковую температуру, то получим поверхность равных температур  изотермическую поверхность с температурой t. Изотермической поверхностью
называется геометрическое место точек в температурном поле, имеющих одинаковую температуру. Так как одна и та же точка тела не может одновременно иметь различные температуры, то изотермические
поверхности не пересекаются. Они либо оканчиваются на поверхности
тела, либо целиком располагаются внутри самого тела.
Пересечение изотермических поверхностей плоскостью дает на
этой поверхности семейство изотерм. Они обладают теми же свойствами, что и изотермические поверхности, т.е. не пересекаются, не обрываются внутри тела, оканчиваются на поверхности либо целиком
располагаются внутри тела.
На рис.1 представлено сечение тела с нанесёнными изотермами,
температуры которых отличаются на величину t. Температура в теле
изменяется только в направлениях l, не совпадающих с изотермической поверхностью. При этом наибольшее изменение температуры на
единицу толщины поверхности происходит в направлении, перпендикулярном к изотермической поверхности (нормаль n).
5
n
l
n
t+t
t
t-t
Рис. 1. Изотермы: n – нормаль; n – расстояние между
изотермами по нормали; t – приращение температуры;
l – произвольное направление изменения температуры
2.2. Градиент температуры
Возрастание температуры внутри пространства (тела) характеризуется градиентом температуры.
Температурным градиентом grad t (К/м) называется предел отношения изменения температуры ∆t к расстоянию ∆n по нормали между соответствующими изотермическими поверхностями при ∆n → 0
(см. рис.1):
 t  t
grad t  lim

.
(2)
n  0  n  n
Градиент температуры является вектором, направленным по нормали к изотермической поверхности (нормаль n) в сторону возрастания температуры и численно равным первой производной от температуры по этому направлению:
t
grad t  n0  ,
(2а)
n
где n0 – единичный вектор, нормальный к изотермической поверхности и направленный в сторону возрастания температур; t / n  производная температуры по нормали n.
Температурный градиент показывает, насколько интенсивно (резко) меняется температура внутри тела, и является важной величиной,
определяющей многие физические явления (появление трещин в хрупком теле от неравномерного нагрева, термические деформации и т.п.).
6
Значение температурного градиента t / n по осям x, y, z в декартовой системе координат вычисляют по формулам
( grad t ) x 
t
t
t
; ( grad t ) y  ; ( grad t ) z  .
x
y
z
(3)
2.3. Тепловой поток. Закон Фурье
Количество тепла, переданное теплопроводностью, определяют на
основе закона Фурье.
Согласно гипотезе Фурье количество теплоты dQ (Дж), проходящей через изотермическую поверхность площадью dF за промежуток
времени d, пропорционально температурному градиенту.
dQ    n 0 
t
 dF  d     grad t  dF  d ,
n
(4)
где  − физическое свойство веществ, называется коэффициентом теплопроводности.
Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности, называется плотностью
теплового потока. Плотность теплового потока (Вт/м2) есть вектор,
определяемый соотношением
q
dQ
t
   n0      grad t .
dF  d
n
(5)
Вектор плотности теплового потока q направлен по нормали к
изотермической поверхности в сторону убывания температуры, так
как теплота самопроизвольно всегда передается от более горячих частей тела к холодным. Таким образом, векторы q и grad t лежат на одной прямой, но направлены в противоположные стороны. Этим и объясняется наличие знака минус в правых частях уравнений (4) и (5).
Скалярная величина вектора плотности теплового потока (Вт/м2) будет
равна
q x  
t
t
t
; q y   ; qz   .
x
y
z
(6)
Многочисленные опыты подтвердили справедливость гипотезы
7
Фурье. Поэтому уравнение (4), а равно и уравнение (5) являются математической записью основного закона теплопроводности – закона Фурье, который формулируется следующим образом: плотность теплового потока, передаваемая теплопроводностью, прямо пропорциональна
градиенту температуры.
Количество теплоты, проходящее в единицу времени через изотермическую поверхность dF, называется тепловым потоком Q,
(Дж/с=Вт). Если градиент температуры для различных точек изотермической поверхности различный, то количество теплоты, которое
пройдет через всю изотермическую поверхность в единицу времени
найдется как
t
Q   q  dF       dF
(7)
n
F
F
Если grad t во всех точках изотермической поверхности имеет
одинаковое значение, то из (7) следует
Q  qF .
(8)
Полное количество теплоты Q (Дж), прошедшее за время  через
изотермическую поверхность F, равно

Q      
0F
t
 dF  d .
n
(9)
Из сказанного следует, что для определения количества теплоты,
проходящего через какую-либо поверхность твердого тела в процессе
теплопроводности, необходимо знать распределение температуры
внутри рассматриваемого тела. Нахождение температурного поля и
является главной аналитической задачей теории теплопроводности.
2.4. Коэффициент теплопроводности
Коэффициент теплопроводности  является физическим параметром вещества и характеризует его способность проводить теплоту.
Коэффициент теплопроводности зависит от рода вещества, его влажности (для пористых тел), температуры и давления. Как правило, коэффициент теплопроводности определяется опытным путем и приводится в справочной литературе.
Существует ряд методов экспериментального определения коэф8
фициента теплопроводности. Большинство из них основано на измерении теплового потока и градиента температуры в заданном веществе.
Коэффициент теплопроводности, Вт/(м·град), при этом определяется
из соотношения
q


(10)
grad t
Из уравнения (10) следует, что коэффициент теплопроводности
численно равен количеству теплоты, которое проходит в единицу времени через единицу изотермической поверхности при градиенте температуры, равном единице. В этом состоит физический смысл коэффициента теплопроводности.
2.5. Дифференциальное уравнение теплопроводности,
условие однозначности
При решении задач, связанных с нахождением температурного
поля, необходимо иметь дифференциальное уравнение теплопроводности. Вывод этого уравнения с использованием метода математической физики приводится в работах 1,2.
Для изотропного однородного тела, физические свойства которого
постоянны, т.е. не зависят от времени, температуры и пространственных координат, дифференциальное уравнение теплопроводности в декартовой системе координат имеет вид
  2t  2 t  2t 
t
c
   2  2  2   q v ,
(11)


x

y

z


где c – массовая теплоемкость материала тела, Дж/(кг·К);  − плотность тела, кг/м3; qv – объемная плотность источников теплоты в теле,
Вт/м3.
Дифференциальное уравнение (11) можно записать и в таком виде:
  2 t  2t  2t  qv
t
 a   2  2  2  
,
(12)

c



x

y

z



где a 
− коэффициент температуропроводности вещества, м2/с.
c
Коэффициент температуропроводности существенен для нестационарных тепловых процессов и характеризует скорость изменения
9
температуры в теле. Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности является мерой теплоинерционных свойств тела.
Из уравнения (12) следует, что изменение температуры во времени
t /  для любой точки тела пропорционально величине a. Иначе говоря, скорость изменения температуры в любой точке тела будет тем
больше, чем больше коэффициент температуропроводности. Поэтому
при прочих равных условиях выравнивание температур во всех точках
пространства будет происходить быстрее в том теле, которое обладает
большим коэффициентом температуропроводности. Величина коэффициента температуропроводности зависит от природы вещества.
Уравнение (11), равно как и (12), называется дифференциальным
уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменениями температуры в любой точке тела, в которой происходит процесс теплопроводности.
Дифференциальное уравнение теплопроводности описывает целый класс явлений переноса теплоты теплопроводностью. Чтобы из
бесчисленного количества этих явлений выделить рассматриваемый
процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности.
Условия однозначности включают в себя:
- геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;
- физические условия, характеризующие физические свойства тела
и окружающей среды (, c ,  и др.);
- временные и начальные условия, характеризующие распределение температур в начальный момент времени. Начальные условия необходимы при рассмотрении нестационарных процессов. В общем
случае начальное условие может быть записано следующим образом:
при   0
t  ( x, y, z ).
(13)
В случае равномерного распределения температуры в теле начальное условие упрощается:
при   0
t = t0= const.
10
(14)
Граничные условия могут быть заданы несколькими способами.
Рассмотрим основные три рода граничных условий. При граничных условиях первого рода имеются значения температуры на поверхности тела. В этом случае требуется определить значение плотности
теплового потока q. При граничных условиях второго рода задана
плотность теплового потока q для поверхности тела в функции времени, т.е. производная от температуры по нормали к поверхности. В этом
случае требуется определить неизвестную температуру другой поверхности стенки. При граничных условиях третьего рода известны
температуры сред, омывающих с разных сторон стенку, и коэффициенты теплоотдачи между стенкой и средами. Требуется определить величину плотности теплового потока q.
В данной лабораторной работе будут обеспечены граничные условия первого рода.
Простейшей задачей данного типа может служить определение температурного
t
поля в плоской однослойной стенке (рис.2)
при стационарном тепловом режиме, т.е.
t(х)
dt/dτ=0,
tw1
(15)
а также при отсутствии внутренних источников теплоты, т.е.
tw2
q
Cp
q

x
Рис. 2. Плоская
однослойная стенка
 0.
(16)
Плоской называют стенку, толщина которой δ значительно меньше двух других характерных размеров (ширины и длины). В
этом случае можно пренебречь отводом теплоты через торцы стенки, считая, что плотность теплового потока q направлена перпендикулярно большей поверхности стенки
вдоль оси х (см. рис. 2).
Для стационарного (установившегося во времени) теплового режима в случае твёрдого тела с однородными свойствами при постоянной теплопроводности λ(t)=const уравнение Фурье для декартовой системы координат имеет вид
11
 2t
 2t
 2t


 0.
 x2  y2  z2
(17)
В случае изменения температуры только по одной координате х
(по толщине), будет справедливо
 2t
 2t

 0.
2
2
y
z
(18)
Дифференциальное уравнение теплопроводности в этом случае
примет вид
d 2t
 0.
(19)
d x2
Найдём закон распределения температуры по толщине стенки
при граничных условиях первого рода:
при х = 0 t = tW1;
(20)
при х = δ t = tW2.
(20а)
После двойного интегрирования уравнения (9) получим его общее решение
t=С1х+С2,
(21)
где С1 и С2 – произвольные постоянные, определяемые граничными
условиями (20).
В случае х=0 в (21) и на основании заданных граничных условий
(20) получим
tW1=С2.
(22)
При х = δ на основании (20а) и (21)
tW2=С1 δ+С2=С1 δ+ tW1,
(23)
откуда
С1 
t w2  t w1


12
(24)
Таким образом, частное решение уравнения (9) при граничных условиях (10) имеет вид
t ( x) 
t w 2  t w1
 x  t w1 .

(25)
Из (25) видно, что температура t(х) линейно зависит от значения х.
Эта зависимость t(х)=f(х) по толщине стенки показана на рис.2.
Плотность теплового потока q (см. рис.1) может быть определена
из закона Фурье, в данном случае имеющего вид
q  - grad t  -  
dt

dx
(26)
Дифференцируя распределение температуры по толщине стенки
(15), получим
dt t w 2  t w1


dx

(27)
После подстановки (27) в (26) можно определить величину плотности теплового потока по выражению
q  - 
dt 
 (t w1  t w2 ).
dx 
(28)
Отношение λ/δ=k носит название тепловой проводимости стенки,
а обратная ей величина δ/λ=R называется термическим сопротивлением стенки.
Количество теплоты, переданное через плоскую стенку в единицу
времени, вычисляется на основании (18) по следующей формуле:
Q  qF 

F (t w1  t w 2 ) ,

(29)
где F – площадь поверхности стенки, м2.
Определение теплопроводности при граничных
условиях первого рода
При необходимости определения значения теплопроводности по
известным значениям температуры на поверхности плоской стенки
13
при стационарном режиме можно использовать выражение

q 

t w1  t w2
(30)
Известно, что теплопроводность зависит от температуры, поэтому
в данном случае полученное значение теплопроводности считается определенным для средней температуры:
t
t w1  t w 2

2
(31)
Значение теплопроводности материала определяется экспериментально и преимущественно стационарным методом. Несмотря на свою
методическую простоту, практическое осуществление сталкивается с
трудностями создания одномерного температурного поля в исследуемых образцах и учёта тепловых потерь. Стационарные методы связаны
со значительным временем выхода установки на стационарный тепловой режим. Имитационные установки позволяют избежать этих трудностей.
3. Описание экспериментальной установки
В экспериментальной установке применён метод имитационного
математического моделирования. Экспериментальная установка состоит из персонального компьютера (ПЭВМ) со стандартными органами управления (клавиатура и мышь компьютера) и имитационной
математической модели лабораторного стенда для определения коэффициента теплопроводности методом плоской стенки. C помощью органов управления вводятся исходные данные эксперимента и производится снятие показаний с датчиков.
Лабораторный стенд экспериментальной установки для определения теплопроводности (рис. 3) состоит из нагревательного элемента 1,
плоской стенки 2, теплоизоляции 3, автотрансформатора 4, регуляторов площади поверхности плоской стенки 5 и толщины слоев стенки 6,
списков материалов слоев стенки 7, датчиков измерения температуры
внутренней 8 и наружной 9 поверхностей стенки.
14
7
6
2
3
1
10
8
5
9
4
Рис. 3. Лабораторный стенд экспериментальной установки для определения
теплопроводности плоской стенки (вид на экране монитора)
Тепловой поток через стенку создается электрическим нагревателем 1. Изменение мощности нагревателя производится изменением
напряжения в цепи нагревателя. Для этого нужно поместить курсор
мыши на автотрансформатор 4 и щелкнуть левой клавишей мыши. На
экране компьютера появится панель автотрансформатора (рис. 4), на
которой имеются регулятор напряжения 3, шкала прибора 1 и кнопка
выключения панели 2.
1
2
3
Рис.4. Автотрансформатор:1− шкала напряжения; 2− кнопка выключения
панели; 3− регулятор напряжения
Для повышения напряжения нужно поместить курсор мыши на
верхнюю кнопку регулятора 3 и нажать левую клавишу мыши, для
снижения напряжения − на нижнюю кнопку регулятора. Значение напряжения отображается на шкале 1. После задания напряжения нужно
щелкнуть по кнопке 2 для выключения панели автотрансформатора.
15
Значение электрического сопротивления нагревателя отображается на
омметре 10 (см. рис. 3).
Изменение площади поверхности плоской стенки производится
регулятором 6 аналогично изменению напряжения. Диапазон изменения площади поверхности − от 0,04 до 0,25 м2. Значение площади поверхности отображается слева от регулятора 5. Регуляторами 6 устанавливается толщина слоя стенки от 0 до 300 мм.
Материал стенки выбирается из списка 7. Для выбора материала
необходимо установить курсор мыши на кнопку справа от списка и
щелкнуть левой клавишей мыши, из раскрывшегося списка нужно выбрать материал слоя. Название выбранного материала выводится внутри списка.
Измерение температуры на внутренней
и наружной поверхностях производится датчиками 8 и 9. Для определения температуры
нужно установить курсор мыши на датчик и
щелкнуть левой клавишей мыши. На экране
появится изображение термометра (рис. 5),
по показанию которого определяется температура. Для выключения панели прибора
щелкнуть по кнопке 2.
1
Измерение температуры по толщине
слоя производится датчиками, установленными в двух ближних к нагревателю слоях
стенки. Датчики располагаются в слое толщиной 20 мм и более. Определение температуры выполняется в следующей последова2
тельности:
- установить курсор мыши на слое, в котором производится измерение, и щелкнуть
левой клавишей. На экране появится панель
с изображением выбранного слоя стенки 1
(рис. 6), датчиков температуры 2 и 3, глубины установки датчиков 4, которая отсчитыРис. 5. Термометр:
1 − шкала; 2 – кнопка "OK" вается от поверхности, ближней к нагревавыключения панели
тельному элементу;
- поместить курсор мыши на один из датчиков и щелкнуть левой
клавишей, на экране появится изображение термометра (см. рис. 5);
- произвести измерение температуры и закрыть панель при помощи кнопки 2.
16
2
1
3
2
5
4
Рис.6. Измерение температур внутри слоя: 1− слой стенки; 2− датчики температуры на наружных поверхностях стенки; 3− датчики температуры внутри слоя;
4 − глубина установки датчиков температуры; 5− кнопка выключения панели
После проведения замеров температуры по толщине слоя стенки
панель измерения температур внутри слоя выключают кнопкой 5 (см.
рис. 6).
4. Порядок выполнения работы
Для выполнения работы студенты должны знать теоретические
положения данного раздела теплотехники, а также иметь навыки работы на компьютере.
Работу выполняют в следующей последовательности:
1. Ознакомиться с работой экспериментальной установки.
2. Получить у преподавателя вариант задания для выполнения
работы (прил. 1).
3. Подготовить бланки «Протокол эксперимента» (прил. 2) и «Результаты обработки данных» (прил. 3).
4. Выполнить экспериментальную часть работы.
4.1. Запустить программу «Теплопроводность плоской стенки». Полностью развернуть окно программы. На экране
компьютера будет изображён вид лабораторного стенда
экспериментальной установки (см. рис. 3.)
4.2. Задать материал стенки и её толщину (толщину второго и
третьего слоя установить равной 0).
4.3. Задать требуемую площадь поверхности стенки.
4.4. Установить необходимое напряжение в цепи нагревателя
(первоначально установить не более 20% максимального
17
значения напряжения).
4.5. Измеренные значения tw1 и tw2 и температуру по толщине
стенки (см. рис. 6) занести в протокол эксперимента (см.
прил. 2). С целью уменьшения погрешности измерения
температуры tw1 и tw2 должны отличаться друг от друга не
менее чем на 3%, в противном случае требуется увеличить
напряжение в цепи нагревателя.
4.6. Данные измерений занести в протокол эксперимента (см.
прил. 2).
5. Выполнить обработку полученных данных. Результаты занести
в таблицу «Результаты расчётов» (см. прил. 3).
6. Оформить отчёт.
5. Обработка экспериментальных данных
5.1. Определить плотность теплового потока через плоскую стенку.
Единственным источником теплоты в данном случае является нагревательный элемент.
Тепловой поток, подводимый к стенке от нагревательного элемента, зависит от мощности нагревателя и вычисляется по формуле:
U2
Q
,
Rн
(32)
где U – напряжение в цепи нагревателя, В; RН − сопротивление нагревателя, Ом.
Следовательно, плотность теплового потока q (Вт/м2) через стенку
можно определить по формуле
U2
q
,
Rн  F
(33)
F − площадь поверхности плоской стенки, м2.
5.2. Определить коэффициент теплопроводности λ материала
стенки в первом тепловом режиме (пп. 4.4, 4.5 раздела «Порядок выполнения работы»).
5.2.1. Теплопроводность λ материала вычисляется по формуле
где
18

q 

t w1  t w 2
(34)
5.2.2. На основании формулы (31) определить температуру tj,
для которой справедливо данное значение теплопроводности. Результаты расчетов занести в таблицу (см. прил. 3).
5.3. Сравнить результаты полученной графической зависимости со
справочными данными (прил. 7).
5.4. Построить графическую зависимость температуры от толщины стенки t(δ).
6. Требования к отчёту
Отчет должен содержать:
1) цель, задачи, оборудование и оснащение лабораторной работы;
2) краткое изложение теоретических положений;
3) принципиальную схему лабораторного стенда экспериментальной установки;
4) протокол эксперимента;
5) обработку результатов эксперимента с проведением необходимых расчётов и построением графиков полученных зависимостей;
6) вывод, содержащий анализ результатов работы, а также перечень факторов и характер их влияния на интенсивность передачи теплоты через плоскую стенку.
Контрольные вопросы
1. Физический смысл коэффициента теплопроводности.
2. Какую стенку допустимо считать плоской?
3. Вид дифференциального уравнения теплопроводности плоской
стенки.
4. Формула для определения теплового потока через плоскую
стенку.
5. Формула количества теплоты, проходящего через плоскую
стенку.
6. Факторы, влияющие на интенсивность передачи теплоты теплопроводностью через плоскую стенку.
ЛАБОРАТОРНАЯ РАБОТА №2
ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛА
МЕТОДОМ ЦИЛИНДРИЧЕСКОЙ СТЕНКИ
19
1. Цели и задачи работы
Цели лабораторной работы: закрепление знаний по разделу
«Стационарная теплопроводность»; получение навыков опытного определения коэффициента теплопроводности цилиндрической стенки
при стационарном тепловом режиме.
Задачи исследования:
 определить экспериментальным путём коэффициент теплопроводности материала методом цилиндрической стенки;
 установить факторы, влияющие на интенсивность передачи теплоты через цилиндрическую стенку.
Оборудование и оснащение: имитационная экспериментальная установка по определению стационарной теплопроводности заданного
материала методом цилиндрической стенки.
2. Теоретические основы
Расчет передачи тепла через цилиндрическую стенку (рис.7) при
граничных условиях первого рода, т.е. когда задано распределение
температур на поверхности, основывается на дифференциальном уравнении теплопроводности Фурье (см. «Лабораторная работа
№ 1.Раздел «Теоретические основы»).
t
t(r)
tw1
tw1
tw2
tw2
r1
q
r2
r
Рис. 7. Цилиндрическая однослойная
стенка
20
Уравнение Фурье для декартовой системы координат
 2t
 2t
 2t


0
 x2  y2  z 2
(1)
в цилиндрической системе координат примет вид
 2t 1 t 1  2t  2t



 0.
 r 2 r  r r 2  2 z 2
(2)
Дифференциальное уравнение теплопроводности бесконечной однослойной цилиндрической стенки с постоянными температурами tw1 и
tw2 соответственно на внутренней (r=r1) и внешней (r=r2) поверхностях
стенки и постоянным коэффициентом теплопроводности стенки  во
всех направлениях запишется в виде
d 2 t 1 dt

 0.
dr 2 r dr
(3)
Найдём закон распределения температуры в однослойной цилиндрической стенке при граничных условиях первого рода:
при r=r1
t = tw1;
(4)
при r=r2
t = tw2,
(4 а)
где r − текущая координата, м; r1 − внутренний радиус цилиндрической стенки, м; r2 − наружный радиус цилиндрической стенки, м.
Представим (3) в форме
1 dt  dt 
 r   0.
r dr  dr 
(5)
После первого интегрирования получим
r
dt
 C1 ;
dr
21
(6)
dt  C1
dr
,
r
(7)
откуда после второго интегрирования получим общее решение уравнения (3):
t(r)=C1lnr+C2.
(8)
Постоянные интегрирования С1 и С2 определим, подставив граничные условия (4) и (4а) в (8):
при r=r1
tw1=С1ln r1+C2;
(9)
при r=r2
tw2=С1ln r2+C2.
(9а)
Вычитая из (9а) выражение (9), получим
tw2 tw1=C1 ln r2 − C1 ln r1=C1 ln (r2/r1).
(10)
C1 = (tw2 tw1)/ ln(r2/r1).
(11)
Откуда
Из (9) выразим и найдём С2:
C2=tw1С1ln r1= tw1−[( tw2− tw1)/ ln (r2/r1)]ln r1.
(12)
Подставив значения С1 и С2 в уравнение (8), получим частное решение уравнения (3) при граничных условиях первого рода:
r
r
t (r )  tw1  tw1  tw2  1 ,
r
ln 2
r1
ln
(13)
где r − текущий радиус цилиндрической стенки, м.
Плотность теплового потока q через единицу длины цилиндрической стенки определяется на основании закона Фурье:
22
q  
 t  t   t  t 
dt
  w2 w1  w1 w2 
r
r
dr
r ln 2
r ln 2
r1
r1
(14)
Количество теплоты, проходящее через цилиндрическую стенку,
можно определить по формуле
Q  qFl  q 2 rl 
2 l (t w1  t w2 )
,
ln(r2 / r1 )
(15)
где F – площадь поверхности стенки, м2; l длина цилиндрической
стенки, м.
В практических расчётах используется линейная плотность теплового потока qL (Вт/м), равная тепловому потоку, отводимому от стенки
длиной 1м.
Определение теплопроводности цилиндрической стенки
при граничных условиях первого рода
При необходимости определения значения теплопроводности по
известным значениям температуры на поверхности цилиндрической
стенки при стационарном режиме можно использовать выражение
d
q L ln 2
d1


(16)
 t w1  t w 2 
Полученное значение теплопроводности считается определенным для средней температуры:
t t
t  w1 w 2 
(17)
2
3. Описание экспериментальной установки
Работа выполняется на установке, аналогичной используемой в
лабораторной работе по определению теплопроводности методом плоской стенки (см. «Лабораторная работа № 1. Раздел 2 «Теоретические
основы»).
Лабораторный стенд экспериментальной установки (рис. 8) состоит из нагревательного элемента 1, цилиндрической стенки 2, тепло23
изоляции 3, автотрансформатора 4, регуляторов высоты цилиндрической стенки 5, диаметра нагревателя 11 и толщины слоев стенки 6,
списков материалов слоев стенки 7, датчиков измерения температуры
внутренней 8 и наружной 9 поверхностей стенки.
2
6
7
3
1
10
9
5
8
11
4
Рис. 8. Лабораторный стенд экспериментальной установки
(вид на экране монитора)
Управление работой установки осуществляется аналогично установке, используемой в лабораторной работе № 1 (см. «Лабораторная
работа № 1. Раздел 3 «Описание экспериментальной установки»).
Изменение высоты цилиндрической стенки и диаметра нагревателя производится регуляторами 5 и 11 соответственно. Диапазоны изменения высоты стенки от 200 до 500 мм, диаметра от 10 до 200 мм.
Значения параметров отображаются слева от регуляторов 5 и 11. Регулятором 6 устанавливается толщина слоя стенки. Толщина слоя стенки
изменяется от 0 до 120 мм.
4. Порядок выполнения работы
9.
7. Ознакомиться с работой экспериментальной установки.
8. Получить у преподавателя вариант задания для выполнения
работы (прил.4).
Подготовить бланки «Протокол эксперимента» (прил. 5) и «Ре24
зультаты расчётов» (прил. 4).
10. Выполнить экспериментальную часть работы.
10.1. Запустить программу «Теплопроводность цилиндрической стенки». Полностью развернуть окно программы. На экране компьютера
будет изображён вид лабораторного стенда экспериментальной установки (см. рис. 8)
10.2. Задать материал стенки и её толщину (толщину второго и
третьего слоя установить равной 0).
10.3. Задать высоту стенки и диаметр нагревателя.
10.4. Установить необходимое напряжение в цепи нагревателя (первоначально установить напряжение не более 20% максимального значения).
10.5. Измеренные значения tw1 и tw2 и температуру по толщине стенки
(см. рис. 6) занести в протокол эксперимента (см. прил. 5). С целью
уменьшения погрешности измерения температуры tw1 и tw2 должны отличаться друг от друга не менее чем на 3%, в противном случае требуется увеличить температуру нагревателя (напряжение в цепи нагревателя).
10.6. Данные измерений занести в протокол эксперимента (см. прил.
5).
11. Выполнить обработку экспериментальных данных. Результаты
занести в таблицу «Результаты расчётов» (см. прил. 6).
12. Оформить отчёт.
5. Обработка экспериментальных данных
5.1. Определить плотность теплового потока через цилиндрическую стенку.
Плотность теплового потока qL через стенку зависит от мощности
источника теплоты (нагревателя) и определяется по формуле
U2
qL 
,
(18)
Rн  L
где U − напряжение в цепи нагревателя, В; RН − сопротивление нагревателя, Ом; L −высота цилиндрической стенки, м.
5.2. Определить коэффициент теплопроводности λ материала
стенки в первом тепловом режиме (пп. 4.4, 4.5 раздела «Порядок выполнения работы»).
5.2.1. Теплопроводность λ материала цилиндрической стенки
определяется по формуле
25
d2
d1

.
 tw1  tw 2 
qL ln
(19)
5.3. По формуле (17) определить среднее значение температуры,
для которой справедливо данное значение теплопроводности.
5.4. Результаты расчетов занести в таблицу (см. прил. 3).
5.5. Сравнить результаты полученной графической зависимости
со справочными данными (прил. 7).
5.6. Построить графическую зависимость температуры от толщины стенки t(δ) .
5.7. Проанализировать полученные результаты.
6. Требования к отчёту
Отчет должен содержать:
7) цель, задачи, оборудование и оснащение лабораторной работы;
8) краткое изложение теоретических положений;
9) принципиальную схему лабораторного стенда экспериментальной установки;
10)
протокол эксперимента;
11)
обработку результатов эксперимента с проведением необходимых расчётов и построением графиков полученных зависимостей;
12)
вывод, содержащий анализ результатов работы, а также
перечень факторов и характер их влияния на интенсивность передачи
теплоты через цилиндрическую стенку.
Контрольные вопросы
7. Что называется теплопроводностью?
8. Вид дифференциального уравнения теплопроводности цилиндрической стенки.
9. Формула для определения теплового потока через цилиндрическую стенку.
10. Формула количества теплоты, проходящего через цилиндрическую стенку.
11. Что называется термическим сопротивлением стенки.
12. Факторы, влияющие на интенсивность передачи теплоты теплопроводностью через цилиндрическую стенку.
26
Приложение 1
Варианты заданий
Номер
Материал
варианта слоя стенки
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Алюминий
Бериллий
Ванадий
Вольфрам
Германий
Железо
Золото
Кальций
Кобальт
Медь
Никель
Платина
Серебро
Тантал
Титан
Хром
Алюминий
Вольфрам
Железо
27
Толщина
стенки
, мм
Площадь
поверхности
стенки F, м2
200
300
200
300
200
300
200
300
200
300
200
300
200
300
200
300
250
300
300
0,04
0,09
0,16
0,25
0,09
0,16
0,25
0,04
0,09
0,16
0,25
0,04
0,09
0,16
0,25
0,04
0,16
0,25
0,25
Приложение 4
Варианты заданий
Номер
Материал
варианта слоя стенки
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Алюминий
Бериллий
Ванадий
Вольфрам
Гафний
Германий
Железо
Золото
Кальций
Кобальт
Медь
Никель
Платина
Серебро
Тантал
Титан
Хром
Алюминий
Вольфрам
Диаметр
нагревателя,
мм
Толщина
стенки
, мм
Высота
цилиндрической
стенки L, мм
100
100
100
100
100
100
100
100
100
100
100
100
150
150
150
150
150
150
150
120
130
140
150
180
100
120
140
170
200
250
300
120
140
180
120
140
250
300
200
200
200
200
200
200
200
200
300
300
300
300
300
300
300
300
300
300
300
28
Приложение 2
Протокол эксперимента
Толщина
Материал
стенки
, мм
Площадь
поверхности стенки
F, м2
Сопротивление
нагревателя
Rн, Ом
Напряжение
на
нагревателе
U, В
Температура на
поверхностях
стенки,
K
tW1
tW1
Глубина
установки
термопар, мм
1
2
3
Приложение 3
Результаты расчётов
Материал
Тепловой поток
q, Вт/м2
29
Коэф.
теплопроводности
λj, Вт/(мК)
Средняя
температура
tj, K
4
Температура, K
t1
t2
t3
t4
Приложение 5
Протокол эксперимента
ТолщиДиаметр
на
Материал нагреватестенки
ля, мм
, мм
Высота
цилиндрической
стенки
L, м
Сопротивление
нагревателя
Rн, Ом
Напряжение
на
нагревателе
U, В
Температура на
поверхностях
стенки,
K
tW1
tW1
Глубина
установки
термопар,
мм
1
2
Приложение 6
Результаты расчётов
Материал
Тепловой поток
q, Вт/м2
30
Коэф.
теплопроводности
λj, Вт/(мК)
Средняя
температура
tj, K
3
Температура,
K
4
t1
t2
t3
t4
Приложение 7
Значения коэффициента теплопроводности материалов
в зависимости от температуры
Материал
Алюминий
Бериллий
Ванадий
Вольфрам
Гафний
Германий
Железо
Золото
Кальций
Кобальт
Медь
Никель
Платина
Серебро
Тантал
Титан
Хром
Предел
температуры,
К
934
1551
2160
3680
2503
1211
1808
1338
1112
1768
1357
1726
2045
1235
3269
1933
2130
Температура, К
250
300
400
500
600
800
1000
235
235
31
180
24
75
87
321
210
110
406
98
71,8
429
57
23
100
237
200
31
174
23
60
80
317
201
100
401
91
71,6
429
58
21
94
240
160
31
159
23
43
70
311
189
85
393
80
71,8
425
58
20
91
236
139
32
146
22
34
61
304
182
75
386
72
72,3
419
59
20
86
231
126
33
137
21
27
55
298
178
67
379
66
73,2
412
59
19
81
218
106
36
123
21
20
43
284
153
58
366
68
75,6
396
59
19
71
91
38
118
21
17
32
270
116
52
352
72
79
379
60
21
65
31
Библиографический список
1. Теплотехника: Учеб. для вузов/ В.Н.Луканин, М.Г.Шатров и др.; Под ред.
В.Н.Луканина. – 3-е изд., испр. – М.: Высшая школа, 2002. – 673 с.
2. Михеев М.А., Михеева И.М. Основы теплопередачи. – М.: Энергия, 1993.
3. Теплопередача В.П.Исаченко., В.А.Осипова, А.С.Сукомел. – 2-е изд. М.:
Энергия,1969. – 440 с.
4. Теплотехника В.Л.Ерофеев, П.Д Семенов, А.С.Пряхин: Учебник для вузов/Под ред. В.Л. Ерофеева. – М.:ИКЦ «Академкнига»,2006. – 456 с.
5. Юдаев Б.Н. Техническая термодинамика. Теплопередача: Учебник для вузов. – М.:Высш.шк. 1988. – 470 с.
ОГЛАВЛЕНИЕ
Лабораторная работа № 1. ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ
МАТЕРИАЛА МЕТОДОМ ПЛОСКОЙ СТЕНКИ ................................................. 3
Лабораторная работа № 2. ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ
МАТЕРИАЛА МЕТОДОМ ЦИЛИНДРИЧЕСКОЙ СТЕНКИ ............................... 19
Приложение 1................................................................................................... 27
Приложение 2................................................................................................... 28
Приложение 3................................................................................................... 29
Приложение 4................................................................................................... 28
Приложение 5................................................................................................... 30
Приложение 6................................................................................................... 30
Приложение 7................................................................................................... 31
Библиографический список............................................................................. 32
32
Учебное издание
ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ
ПРИ СТАЦИОНАРНОМ ТЕПЛОВОМ РЕЖИМЕ
Методические указания
к выполнению лабораторных работ
по дисциплинам «Теплотехника», «Тепломассообмен»
Составители:
Анатолий Степанович Ненишев,
Александр Леонидович Иванов
***
Редактор И.Г.Кузнецова
***
Подписано к печати 2008 г.
Формат 6090 1/16. Бумага писчая
Оперативный способ печати
Гарнитура Times New Roman
Усл. п. л. 2,0 , уч.-изд. л. 2,0
Тираж 100 экз. Заказ № ___
Цена договорная
Издательство СибАДИ
644099, г. Омск, ул. П. Некрасова, 10
Отпечатано в ПЦ издательства СибАДИ
644099, г. Омск, ул. П. Некрасова, 10
33