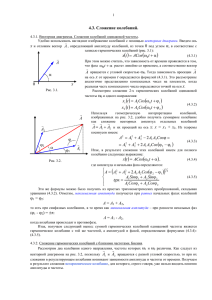
Потенциальная энергия
advertisement

Энергия гармонических колебаний Колеблющееся тело обладает кинетической и потенциальной энергией. Кинетическая энергия колеблющейся материальной точки с массой m вычисляется по формуле (1.29) с учетом (3.11): Потенциальная энергия материальной точки, совершающей колебания под действием упругой силы вычисляется по формуле (1.32) с учетом (3.9) и (3.7) Полная энергия гармонических колебаний равна Учитывая, что получим Из формулы (3.15) следует, что полная энергия при гармонических колебаниях не зависит от времени, т. е. остается постоянной. Следовательно, выполняется закон сохранения механической энергии. Второй важный вывод: энергия при гармонических колебаниях пропорциональна квадрату амплитуды и квадрату частоты. Векторная диаграмма При рассмотрении многих вопросов, в частности, при сложении колебаний одинакового направления и частоты бывает удобно гармоническое колебание представить в виде векторной диаграммы. Векторная диаграмма строится следующим образом: надо изобразить вектор, длина которого равна амплитуде, угол наклона к оси абсцисс равен начальной фазе. Если привести этот вектор во вращение с угловой скоростью ω0, равной круговой частоте колебаний, то проекция его конца на выбранную ось будет изменяться по гармоническому закону. На рис. 3.3 представлена векторная диаграмма для гармонического колебания в момент времени t = 0. Рис.3.3 Метод векторных диаграмм удобен при сложении колебаний одинаковой частоты. Сложение гармонических колебаний одинакового направления и одинаковой частоты Пусть надо сложить два колебания, которые определяются уравнениями Представим каждое колебание в виде вектора и найдем по правилам сложения векторов результирующий вектор (рис. 3.4). Рис.3.4 Результирующее колебание равно сумме складываемых колебаний, т. е. Так как угловая скорость ω0 у складываемых векторов одинакова, то результирующий вектор тоже вращается со скоростью ω0. Тогда уравнение результирующего колебания имеет вид Результирующую амплитуду можно найти по теореме косинусов По формулам приведения в тригонометрии Тогда квадрат результирующей амплитуды равен Результирующая амплитуда равна Начальная фаза результирующего колебания находится из выражения для тангенса угла α: Значение угла α можно найти из следующего равенства Проанализируем выражение для амплитуды (3.17). Это выражение показывает, что значение амплитуды результирующего колебания зависит от разности фаз складываемых колебаний. Если разность фаз (α2 - α1) = 2nπ, где n = 0, 1, 2, ..., то A = A1 + A2 - это максимальное значение для результирующей амплитуды. Если разность фаз (α2 - α1) = (2n+1)π, где n = 0, 1, 2, ..., то A = A1 - A2 - это минимальное значение амплитуды. Следовательно, колебания в зависимости от разности фаз могут усиливать или ослаблять друг друга. Этот важный вывод используется при описании интерференции волн.