170101 Уч. пособие Баллистика Физические основы
реклама
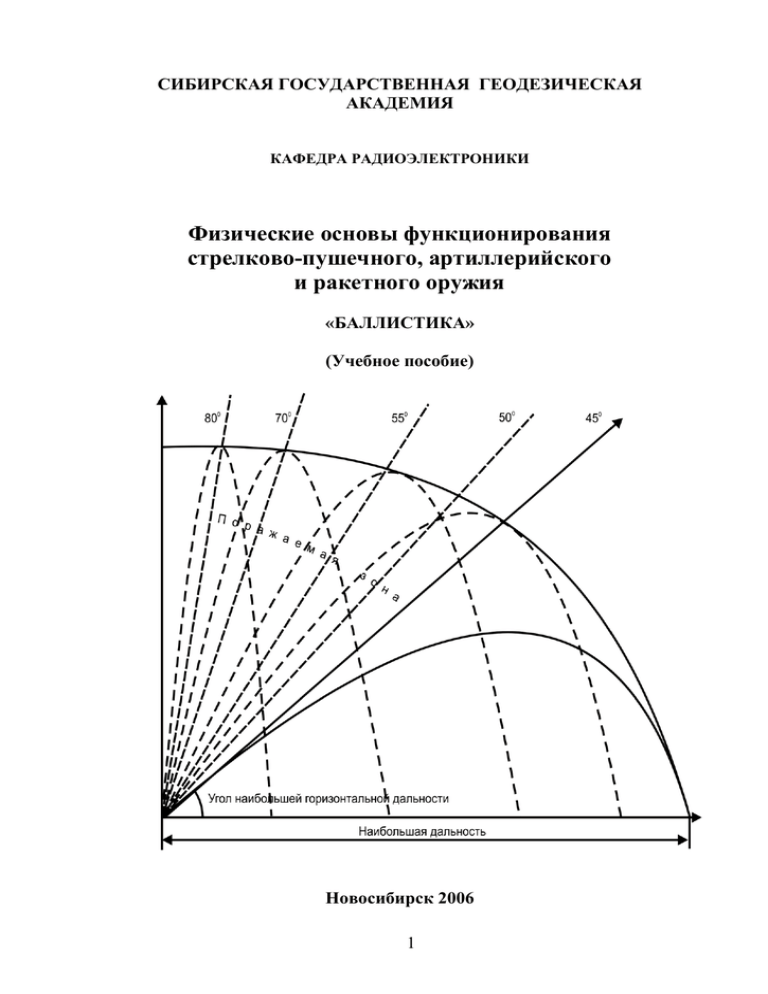
СИБИРСКАЯ ГОСУДАРСТВЕННАЯ ГЕОДЕЗИЧЕСКАЯ АКАДЕМИЯ КАФЕДРА РАДИОЭЛЕКТРОНИКИ Физические основы функционирования стрелково-пушечного, артиллерийского и ракетного оружия «БАЛЛИСТИКА» (Учебное пособие) Новосибирск 2006 1 Настоящее учебное пособие составлено доцентами кафедры радиоэлектроники С.А. Горовым, С.Г. Губиным по дисциплине ―Испытания и эксплуатация техники (по областям и видам)‖ и содержит материал, включающий сведения по вопросам: внутренней баллистике; внешней баллистике. Учебное пособие предназначено для использования на занятиях по темам: «Физические основы функционирования стрелково-пушечного, артиллерийского и ракетного оружия», «Основания устройства и проектирования стрелково-пушечного, артиллерийского и ракетного оружия», «Основы технической эксплуатации военной техники (по областям и видам)», а также для решения практических задач. Рецензенты: Заведующий кафедрой естественнонаучных дисциплин НВВКУ: академик Академии наук высшей школы РФ, доктор технических наук, профессор Е.И. Аверков. Заведующий кафедрой радиоэлектроники СГГА, профессор, кандидат технических наук А.В. Кошелев. 2 СОДЕРЖАНИЕ: Введение. Глава I. Краткие сведения из истории развития взрывчатых веществ, баллистики и теории стрельбы. 1.1. Сведения из истории изобретения и применения взрывчатых веществ. 1.2. Сведения из истории развития внутренней и внешней баллистики. 1.3. Сведения из истории развития теории стрельбы Глава II. Взрывчатые вещества. 2.1. Взрывчатые вещества как источник энергии. 2.2. Явление взрыва и виды взрывчатых превращений. 2.3. Классификация ВВ. Основные представители инициирующих и бризантных ВВ. 2.3.1. Основные характеристики пороха. 2.4. Законы горения пороха. 2.5. Форма и маркировка порохов. Глава III. Сведения из внутренней баллистики. . 3 3.1. Предмет и задачи внутренней баллистики. 3.2. Сущность явления выстрела. Периоды выстрела. 3.3. Прочность и живучесть ствола. Действие нагара на ствол оружия. 3.4. Движение снаряда по каналу ствола. 3.5. Начальная скорость снаряда. 3.6. Кинетическая энергия снаряда. 3.7 Явление отдачи. 3.8. Образование угла вылета. Меры соблюдения его однообразия. 3.9. Особенности выстрела из миномета. 3.10.Особенности выстрела из реактивного оружия. Глава IV. Сведения из внешней баллистики. 4.1. Предмет и задачи внешней баллистики. Траектория снаряда и еѐ элементы. 4.2. Движение снаряда под действием силы тяжести. 4.3. Движение снаряда в воздухе. 4.4. Движение вращающегося снаряда в воздухе. 4.5. Особенности полета не вращающихся снарядов. 4.6. Общие свойства траектории снаряда в воздухе. 4.7.Табличные условия. Влияние метеорологических условий на полѐт снаряда. Глава V.Форма траектории и еѐ практическое значение. 5.1. Виды траекторий и их применение. 5.2. Прицельное поражаемое пространство. 5.3. Дальность прямого выстрела. 3 5 7 7 11 15 19 19 19 21 24 26 27 31 31 32 38 46 47 54 55 60 62 64 68 68 70 77 88 93 95 96 103 103 106 111 5.4. Элементы траектории у точки встречи. 5.5. Поражаемое пространство. 5.6. Поражаемое пространство на наклонной местности. 5.7. Прикрытое и мѐртвое пространства. Список литературы Приложение 4 113 119 119 125 131 134 ВВЕДЕНИЕ В практической деятельности инженера по испытаниям, офицера, курсантам, студентам не раз придѐтся столкнуться с проблемой решения задач связанных с основами стрельбы. В практике больше интересует другой вопрос: сколько необходимо патронов (мин, снарядов, гранат, других типов боеприпасов), чтобы поразить ту или иную групповую или одиночную цель? В бою эта задача возникает каждый раз, когда командир поставил задачу: подавить или уничтожить цель. Вопрос о расходе боеприпасов должен решать и руководитель тактического учения с боевой стрельбой при определении необходимого количества патронов (мин, снарядов, гранат) для выполнения той или иной тактической задачи. Определять количество патронов (мин, снарядов, гранат) приходится при составлении Курса стрельб, таблиц стрельбы, определении оценки стрельбы и целого ряда других вопросов, связанных с использованием оружия. Различные условия деятельности командира вызывают и различное решение данной задачи. В боевых условиях расход тех или иных боеприпасов определяется на основе знания правил стрельбы и анализа результатов проведения предыдущих стрельб. В этом случае огромное значение имеет опытность командира, знание им огневых возможностей данного вида оружия, подготовка стреляющих, чтобы, с одной стороны, не допускать неоправданного излишнего расхода боеприпасов (особенно мин и снарядов), а с другой стороны, не сорвать выполнение огневой задачи, назначив явно недостаточное количество патронов (мин, снарядов). Правда, в последнем случае стрельбу иногда можно повторить, однако уже будет упущен элемент внезапности; противник может укрыться, сменить позиции, открыть ответный огонь и т. д. При определении количества боеприпасов на тактических учениях с боевой стрельбой также можно использовать данные проведенных учений. Однако здесь может быть точное решение с применением таблиц стрельбы. Такое решение позволит дать объективную оценку стреляющему подразделению на основе более точных данных. По программе обучения предусмотрен курс с ограниченным временем, за которое сложно в полном объеме усвоить все вопросы, связанные с решением задач по основам стрельбы. Поэтому основной объем времени придется выделить на самостоятельную работу курсантам, студентам для глубокого изучения, данного материала. При работе с различной литературой [1-16], предназначенной для изучения «Основ и правил стрельбы», обнаружены следующие проблемы. Все пособия делают основной упор на стрельбу из артиллерийских орудий и минометов, мало уделяют внимания стрелковому оружию и вооружению мотострелкового батальона. В учебных пособиях ранних выпусков, которые сложно найти в учебных библиотеках ВУЗов, более подробно раскрыта данная 5 проблема, в новых пособиях эта проблема раскрыта несколько ограниченно и необходим определенный опыт, чтобы с ней разобраться. В работе поставлена цель, обобщить разрозненные материалы, изданные в различных пособиях и различных источниках, согласовать их с требованиями, предъявляемыми к курсантам, студентам по изучению данной дисциплины, изложить материал в доступной для запоминания форме, применительно к изучаемой тематике. 6 Глава. I Краткие сведения из истории развития взрывчатых веществ, баллистики, теории вероятностей и теории стрельбы Развитие военного дела и военной науки неразрывно связано с экономическими условиями, с развитием производительных сил на каждом этапе истории. Каждое изобретение в области вооружения, каждое открытие в области теории военного дела находятся в прямой зависимости от достигнутого в данный момент уровня производства. Эта закономерность развития всех наук, в том числе и военной, позволяет правильно понять историю возникновения и развития современной теории стрельбы, правильно оценить ее состояние в настоящее время и предусмотреть основные тенденции в развитии науки. Создание и боевое применение современного огнестрельного оружия основывается на строго научных выводах ряда наук [1-39]. Эти выводы проверены многолетней практикой использования части взрывчатых веществ (ВВ) в качестве источника энергии для метания снарядов. В дальнейшем в пособии будет приведено деление ВВ на составные части. При рассмотрении основ стрельбы сведения из истории развития баллистики вызывают интерес и помогают лучшему и более глубокому усвоению изучаемого материала. Поэтому основному содержанию настоящего учебного пособия предпосылается краткий очерк из истории изобретения взрывчатых веществ, и развития баллистики и теории стрельбы. 1.1Сведения из истории изобретения и применения взрывчатых веществ. Первым известным в истории взрывчатым веществом явился дымный порох, состоящий из смеси селитры, угля и серы. Появление пороха в Европе относят к началу XIV века. Продолжительное время существовало мнение, что порох был изобретен в Германии монахом Бертольдом Шварцем. Однако, еще в середине ХIХ века исторические исследования показали явную ошибочность этого мнения. Изобретение пороха относится к более раннему периоду и объясняется следующим образом. В некоторых районах Китая, Индии и Египта почва содержит в себе селитру, и наблюдаются даже выходы еѐ на поверхность в виде белого налета. Понятно, что селитра была известна там весьма давно. Вероятно, что при разведении костров на этой почве были замечены вспышки, получающиеся при смешивании селитры с углем от костров. Этим можно объяснить, что смесь селитры с углем уже в первых веках до нашей эры употреблялась в Китае как зажигательный состав, а также для составления «потешных огней». Есть основания полагать, что от китайцев и индийцев применение зажигательных смесей перешло к аравитянам (они называли селитру китайской 7 солью, китайским снегом), а от них в VII веке нашей эры — к грекам. Зажигательные смеси появились в Европе и получили название греческого огня. Греческие императоры держали состав огней в строгом секрете для поддержания суеверного ужаса крестоносцев перед греческим огнем. Так, о греческом огне сообщали, что он пожирал даже камни и железо, что вода удваивала его ярость и т. п. В начале XIV века, когда в Европе появилось огнестрельное оружие, т. е. когда начали пользоваться метательным действием пороха, название «греческие огни» уже не встречается в летописях. Полагают, что греческий огонь был довольно близок к пороху и постепенно перешел в порох. В летописях России порох, как метательное средство, упоминается в 1382 году. В 1389 году порох в артиллерии широко использовал Дмитрий Донской. К XV веку были составлены достаточно подробные описания применявшихся на Руси способов приготовления необходимой для пороха селитры. Так, например, первые русские пороходелы собирали в кучи (бурты) золу, навоз, оскребки кожи, ботву различных корнеплодов и т. п. В течение двух лет бурты поливались мочой и перелопачивались, после чего на них появлялся налет селитры. В 1494 году в России был создан первый пороховой завод. До этого порох изготовлялся кустарно. Порох вначале по своему составу был весьма далек от современного: селитру, уголь и серу смешивали поровну. Сначала порох не зернили, а употребляли для стрельбы мякоть. Наиболее целесообразный состав пороха разработал Михаил Васильевич Ломоносов (1711—1765 гг.). Предложенный им состав содержал 75% селитры, 15% угля и 10% серы. В своих трудах «Диссертация о рождении и природе селитры» и «О природе пороха» Ломоносов дал научные толкования пороходелия, указания о совершенствовании порохового производства, руководство по применению порохов, исследования взрывной силы и т. д. После Ломоносова русская пороховая промышленность развивалась на научной основе и не только шла в ногу с зарубежной, но часто и опережала ее. Во второй половине XVIII века возникает потребность в более мощном и качественном порохе, чем существовавший тогда черный порох. Черный порох не удовлетворял войска, во-первых, тем, что при выстреле он давал густое черное облако дыма, которое демаскировало стреляющих и закрывало от них поле боя. Кроме того, порох оставлял в стволе более 50% своего веса в виде нагара. Появление более качественных артиллерийских стволов требовало пороха большей мощности. Первую попытку в этом направлении делает французский химик Бертолле в связи с открытием им в 1786 году хлорноватой кислоты и ее солей, которые в последствии стали называть бертолетовой солью. Он пытался приготовить порох из смеси бертолетовой соли, угля и серы. Однако несколько непредвиденных взрывов с тяжелыми человеческими жертвами заставили его прекратить опыты. 8 В XIX веке работы с взрывчатыми веществами проводились уже на основе достижений естественных наук и, в первую очередь, химии. Только на основе успехов органической химии, которая начала развиваться с 20-х годов, стали возможны два замечательных открытия: нитроклетчатки и нитроглицерина. Открытие нитроклетчатки привело в дальнейшем к поворотному пункту в истории пороха — к изобретению бездымного пороха. Открытие нитроглицерина привело к столь же важному повороту в истории взрывчатых веществ — к открытию явления детонации и бризантных взрывчатых веществ. История разработки и применения взрывчатых веществ в народном хозяйстве и в военных целях в России неразрывно связана с именами русских ученых Н.Н.Зинина, А.А.Фадеева, З.В.Калачева, Д.И.Менделеева, Л.Н.Шишкова, С.В.Панпушко, Г.П.Киснемского и многих других. Николай Николаевич Зинин (1812—1895 гг.) академик, химик-органик, работавший в содружестве с известным артиллеристом В.Ф.Петрушевским, в 1842 году открыл способ превращения нитробензола в анилин, являющийся исходным продуктом для получения многих взрывчатых веществ. В 1853 году Зинин применяет для снаряжения снарядов нитроглицерин, а Петрушевский впервые получает нитроглицерин фабричным способом. В короткий срок им было изготовлено около 3000 кг нитроглицерина. До этого нитроглицерин получали только лабораторным путем. Среди имен ученых, занимавшихся вопросами взрывчатых веществ, необходимо назвать имя преподавателя Михайловского артиллерийского училища Александра Александровича Фадеева (1810—1895 гг.). Фадеев разрешил важнейшую для того времени задачу: он изобрел способ длительного и безопасного хранения дымного пороха путем добавления специальных примесей. К 1846 году Фадеев разработал и начал промышленное изготовление пироксилина и возглавил затем Охтинские пороховые заводы. Ученик Фадеева Леон Николаевич Шишков (1830—1909 гг.) в 50-х годах XIX столетия дал анализ продуктов горения пороха и определил температуру взрывчатого разложения пороха. В 70-х годах ХIХ века практика оружейного дела поставила задачу изыскания бездымного пороха, так как созданные в те годы магазинные винтовки из-за дыма при стрельбе теряли свои преимущества. После многих неудач в 1884 году французскому ученому Вьелю удалось получить бездымный пироксилиновый порох. Французы держали это изобретение в строгом секрете. В 1887—1888 гг. во многих странах приступили к разработке бездымного пороха. В России, на Охтинском пороховом заводе, после настойчивых трудов в конце 1888 года создается образец ружейного бездымного пироксилинового пороха. Доработанный образец этого пороха в конце 1889 года был разрешен для валового выпуска. Этот порох был создан талантливым русским пороходелом З.В. Калачевым. 9 З.В.Калачев родился в 1853 году. После успешного окончания Артиллерийской академии с 1879 года он работает на Охтинском пороховом заводе начальником «мастерских всех испытаний пороха». Здесь он и создает первый отечественный бездымный порох. В 1890 году Охтинский завод выработал более тысячи пудов ружейного пороха, созданного З. В. Калачевым. Весной 1890 года военным и морским министерствами для быстрейшего решения вопросов бездымного пороходелия приглашается великий русский ученый Дмитрий Иванович Менделеев (1834-1907гг.). Менделеев, изучив технологию изготовления бездымного пороха, разработал в 1891 году новый тип нитроклетчатки – пироколлодий, из которого изготовил пироколлоидный порох. Этот порох, годный не только для ружей, но и для орудий (вплоть до 12-дюймовых), получил впоследствии широкое применение. Но царское правительство не сумело и не хотело оградить интересы своей страны от посягательства иностранцев на изобретение великого ученого. Американцы Бернадоу и Конвере, заимствовав изобретение Менделеева, в 1895 году взяли патент на изготовление пироколлоидного пороха, выдавая его за свое открытие. В России имя создателя отечественного бездымного пороха З.В. Калачева и фундаментальные исследования Д.И. Менделеева были преданы забвению. Порох же, созданный их трудами, после некоторой доработки безотказно служил в русско-японскую войну, в Первую мировую войну и после дальнейшего усовершенствования — в Великую Отечественную войну. К концу XIX века относятся работы еще нескольких выдающихся русских пороходелов. В 1891 году в расцвете творческой деятельности погиб крупный специалист по порохам и взрывчатым веществам Семен Васильевич Панпушко (1856—1891 гг.). Его замечательная работа «Заводское приготовление пироксилина и нитроглицерина» была удостоена Михайловской премии. Панпушко является пионером русского снаряжательного дела, исследовавшим вопрос о снаряжении артиллерийских снарядов мелинитом. Неутомимым исследователем в области взрывчатых веществ был русский артиллерист Гавриил Петрович Киснемский. Ему принадлежит заслуга в изготовлении пороха прогрессивного горения, в разработке стабилизатора порохов — дифениламина. Войны начала ХХ века - Русско-японская и Первая мировая война— потребовали колоссальных расходов взрывчатых веществ. Достаточно сказать, что расход боеприпасов в течение 1914—1918 гг. составил, например, для Франции 191 миллион выстрелов, для Англии—170 миллионов, для России— 50 миллионов выстрелов. Такой расход боеприпасов потребовал спешной разработки новых взрывчатых веществ. Из них большое значение приобрели суррогатные взрывчатые вещества. Этот класс взрывчатых веществ был впервые изучен и предложен видным русским химиком И.М.Чельцовым (1848— 1904 гг.). После Великой Октябрьской социалистической революции в России создались благоприятные условия для развития отечественной науки и техники. 10 Большой вклад в дальнейшую разработку теории и практики применения взрывчатых веществ внесли Н.Т.Зверев, А.В.Сапожников, С.П.Вуколов, Е.Г. Гронов, А.А.Дзержкович, В.И.Рдултовский. В 1927—1929 гг. разработаны образцы нового вида нитроглицеринового пороха баллиститного типа с введением 1 % вазелина (НГВ). С 1929 по 1934 гг. вступили в строй несколько цехов и отдельные заводы нитроглицеринового пороха. С 1934 года в СССР освоена валовая фабрикация нитроглицеринового пороха (А.С.Бакаев, Б.П.Фомин, А.Д.Артюшенко и др.). В 1935—1936 гг. был отработан отечественный порох «НБ» для минометных зарядов. В 1939—1940 гг. разработана серия «холодных» нитроглицериновых порохов (НД), принятых в 1941 году на вооружение армии. В 1942—1946 гг. В.С.Тихоновичем и К.Г.Поповой разработаны нитроглицериновые пороха повышенной мощности для 7,62-мм винтовки и 14,5-мм противотанкового ружья. В последующие годы Л.В.Архангельский получил мощный баллистит* для 7,62-мм патронов. Во время Второй мировой войны изготовлялись в значительных количествах тэн и гексоген. Других новых взрывчатых веществ, за исключением нескольких второстепенных, не появилось. Главное внимание, по-видимому, направлялось на увеличение количества производившихся взрывчатых веществ, так как было установлено, что современная химия не в состоянии дать взрывчатые вещества, сила которых превышала бы силу известных уже взрывчатых веществ, например, нитроглицерина, хотя бы в 4 — 5 раз. Задача получения сверхмощного взрывчатого вещества была разрешена средствами современной ядерной физики. Об энергет ических возможностях радиоактивных элементов можно наглядно судить на примере распада урана, при взрыве которого развивается температура порядка 10 миллионов градусов, тогда как максимальная температура взрыва обыкновенных взрывчатых веществ соста вляет примерно 4000 º С. 1.2. Сведения из истории развития внутренней и внешней баллистики История баллистики тесно связана с историей развития арти ллерии. Ряд выдающихся ученых, особенно математиков, занимался вопросами баллистики еще до средних веков. Так, итальянский учѐный Н. Тарталья (XVI век) написал труд «Вопросы и открытия, относящиеся к артиллерийской стрельбе». Баллистикой занимались такие выдающиеся ученые, как Г.Галилей, Э.Торричелли, М.Мерсенн, М.В.Ломоносов, Л.Эйлер, Д.Бернулли. М.Мерсен в 1644 году предложил назвать науку о движении снаряда * Баллистит – одно из наименований пороха. 11 баллистикой (от греческого слова «балло» — бросать, метать). Как самостоятельная, определенная область науки, баллистика получила широкое развитие с середины XIX века. Баллистика обязана многим трудам великих русских математиков Н.И.Лобачевского, П.Л.Чебышева, М.В. Остроградского, замечательным работам воспитанников Михайловской артиллерийской академии А.А.Фадеева, Н.В.Майевского, Н.А.Забудского, В.М.Трофимова, Н.Ф.Дроздова и др. В 1857 году русский химик Л.Н.Шишков, преподаватель артиллерийской академии, публикует совместно с немецким ученым Р.В.Бунзеном первую работу по теории горения порохов. В 1860 году капитан русской армии А.П.Горлов написал статью о движении снаряда в канале нарезного оружия. Часть этой работы была опубликована в 1862 году в отчетах Парижской академии наук. В 1868 году полковник Н.П.Федоров установил влияние условий горения пороха на состав продуктов горения. Эти работы явились основой для развития правильных положений о горении пороха при выстреле и были использованы в дальнейших трудах по внутренней баллистике. К 60-м годам относится изобретение двух основных приборов экспериментальной баллистики, широко применяемых до настоящего времени, — хронографа Ле-Буланже для измерения скорости снаряда (Бельгия) и крешера У.Нобеля для измерения давления пороховых газов (Англия). Из наиболее крупных ученых во второй половине XIX века следует отметить профессора, члена-корреспондента Академии Наук Н.В. Маевского (18231892 гг.). Хотя мировую известность Н.В.Майевский приобрел трудами в области внешней баллистики, но он многое сделал и в деле развития внутренней баллистики. Так, в 1856 году, задолго до опытов Нобеля с крешерными приборами, он создает оригинальный способ определения давления пороховых газов и впервые получает кривую давления газов. Рассчитанная Н.В.Майевским по этим данным пушка показала на проведенных испытаниях значительно лучшие результаты, чем орудия других конструкторов, в том числе и английских. В 1870 году в России был издан первый курс внутренней баллистики, написанный преподавателем Артиллерийской академии полковником П.М. Альбицким. В 1885 году издается курс внутренней баллистики полковника В.А.Пашкевича (Артиллерийская академия), а в 1901 году — Бринка и И.П.Граве (Артиллерийская академия). В последней четверти XIX века внутренняя баллистика обогащается целым рядом законов и открытий, связанных с разработкой и исследованием свойств бездымного пороха. Н.А.Забудский (1853—1917 гг.), выдающийся ученый-артиллерист, пишет труды «О давлении газов бездымного пороха в канале пушки», за который был удостоен большой Михайловской премии (1894 год); «О давлении пороховых 12 газов в канале 3-дюймовой пушки и скоростях в различных сечениях» и другие работы. Начало ХХ века ознаменовалось в истории развития внутренней баллистики работами Н.Ф.Дроздова (1862—1954 гг.), который в 1903 году впервые в мире дал точное решение основной задачи внутренней баллистики. В 1920 году он составил таблицы для определения наибольших давлений и скоростей снаряда в канале ствола. Эти таблицы легли в основу проектирования артиллерийских систем. Работая в Артиллерийской академии по очень широкому кругу вопросов, Н.Ф.Дроздов продолжал свои работы по внутренней баллистике. В 1941году он опубликовал труд «Решение задач внутренней баллистики для бездымного пороха трубчатой формы». В 1947—1948 гг. были изданы еще два труда Дроздова: «О свойствах орудий наибольшего могущества» и «О решении задачи внутренней баллистики для простого и комбинированного зарядов». За эти труды Н.Ф.Дроздов получил звание заслуженного деятеля науки и техники и Сталинскую премию. К выдающимся работам предреволюционного периода относится также труд И.П.Граве «О горении пороха в неизменном объѐме» (1904 год). В 1933— 1936 гг. Граве, будучи начальником кафедры внутренней баллистики, в Артиллерийской академии, создает многотомный, самый полный в мире курс внутренней баллистики. Существенное значение для развития баллистики имели работы Г.П.Киснемского и Г.П.Дымши о поправочных формулах внутренней баллистики. За границей в это время также велись работы по конструированию орудийных систем и по баллистике. Из работ этого периода следует отметить труды французских ученых Шарбонье «Внутренняя баллистика» (1908 год), Мусюго «Курс внутренней баллистики», немецких баллистиков Кранца, Шмица «Курс баллистики», итальянца Бианки и ряда других ученых. После Великой Октябрьской социалистической революции, с 1918 по 1926 гг., велась большая работа в Комиссии особых артиллерийских опытов (Косартоп), руководимой В.М.Трофимовым (1865—1926 гг.). В Комиссию были привлечены выдающиеся ученые: А.Н.Крылов, С.А.Чаплыгин, Н.Е. Жуковский. В Комиссии были подробно разработаны вопросы сверхдальнобойной стрельбы (до 140 км), конструирования новых артиллерийских систем, газодинамики и внутренней баллистики. Этапы развития внешней баллистики во многом совпадают с уже упомянутыми датами из истории внутренней баллистики. И это понятно, так как обе науки очень близки между собой и развиваются в тесной взаимной связи. Как уже указывалось, первый труд о движении снаряда был написан итальянцем Н.Тарталья еще в 1537 году. Однако в этой работе было очень много наивных и неправильных рассуждений; так, например, траекторию Э.Тарталья считал состоящей из двух прямых и закругления в вершине. К началу XVII века относятся работы великого ученого Г.Галилея 1564— 1642 гг. Им было предположено, что траектория снаряда является параболой 13 (1638 год). С этого времени расчеты траекторий производились по формулам параболической теории. В 1721 году член Петербургской Академии Наук Даниил Бернулли (1700—1762 гг.) решил задачу о движении снаряда с учетом силы сопротивления воздуха. Он принимал силу сопротивления воздуха пропорциональной квадрату скорости снаряда. Однако для практики это решение значения не имело из-за чрезвычайной сложности и громоздкости вычислений, и траектории снарядов продолжали рассчитывать, пользуясь параболической теорией. Новая эра в баллистике начинается с работ знаменитого петербургского академика Леонарда Эйлера (1710—1763 гг.). В 1753 году Эйлер дал более простое решение задачи о движении снаряда в воздухе и предложил метод расчета траекторий, который применяется до настоящего времени. До начала ХIХ века баллистикой занимались в различных странах лишь отдельные ученые. С созданием в России в 1820 году Михайловского артиллерийского училища, преобразованного в 1855 году в Михайловскую артиллерийскую академию, было положено начало русской артиллерийской школе. Первым преподавателем баллистики в России был Викентий Александрович Анкудович (1792—1856 гг.). Им же был написан первый курс внешней баллистики (1837 год). Влияние этого курса испытали многие баллистики Запада. Так, например, в курсе Дидиона (Франция) встречаются фразы, целиком взятые из книги Анкудовича. Одним из преподавателей внешней баллистики в Академии был выдающийся математик М. В. Остроградский (1801—1861 гг.). Во время работы в академии Остроградский составил таблицы полета сферических снарядов в воздухе. Именно ему артиллерийская наука обязана созданием математической школы, так необходимой артиллеристам. Основоположником современной внешней баллистики справедливо считается Николай Владимирович Майевский. Майевский тесно связал баллистику с практическими задачами артиллерии. Огромное значение для развития баллистики имели открытые им законы сопротивления воздуха. Майевским впервые разработаны такие разделы баллистики, как вращательное движение снаряда и теория поправок. Фундаментальный курс внешней баллистики, написанный им в 1870 году, оказал сильное влияние на развитие внешней баллистики во Франции, Англии, Италии, Америке. Курсы внешней баллистики Башфорта (1881 год), Сиаччи (1888 год), Шарбонье (1904 год), Кранца (1936 год) во многом следуют курсу Майевского. Продолжателем дела Маевского является его ученик Николай Александрович Забудский, оставивший ряд блестящих работ в области вращательного движения и свойств траектории снаряда в воздухе. Ему принадлежит формула, определяющая крутизну нарезки у дула, необходимую для достижения устойчивости снаряда. Одной из крупнейших работ того времени является труд итальянского баллистика Сиаччи, который разработал новый метод расчета траекторий. Метод Сиаччи применяется и в настоящее время. 14 В ХХ веке перед внешней баллистикой возникли новые задачи: сверхдальняя стрельба и составление точных таблиц. Эти задачи нашли полное разрешение в работах выдающегося баллистика Василия Михайловича Трофимова. Ему принадлежит заслуга объединения ряда крупных ученых для разрешения проблем артиллерийской науки в созданной им Комиссии особых артиллерийских опытов. Одним из ученых, вовлеченных в работу Комиссии, академиком А.Н.Крыловым, в 1918 году был предложен метод численного интегрирования для расчета траекторий и в 1929 году создана современная теория вращательного движения снарядов. В Советском Союзе центром артиллерийской науки являлась Артиллерийская академия имени Дзержинского. За это время в СССР проведены выдающиеся работы по внешней баллистике. Профессором Пугачевым решена общая задача о движении вращающегося снаряда в воздухе. В нашей стране создана и осуществлена на практике теория реактивного движения, основы которой были заложены в работах К. Э. Циолковского и И. В. Мещерского. Работы Н.Е.Жуковского, С.А.Чаплыгина и их учеников С.А.Христиановича и Ф.И.Франкля по аэродинамике и газодинамике дали возможность изучить сопротивление воздуха снарядам, которые движутся со скоростями, близкими к скорости звука и превышающими ее. За годы выполнения пятилетних планов в СССР была создана широкая сеть научно-исследовательских институтов, конструкторских бюро, которые разработали к началу Великой Отечественной войны (1941—1945гг.) все необходимые вопросы баллистики. Выросли ряды ученых-баллистиков, имеющих выдающиеся заслуги: генерал-лейтенант А.А.Благонравов, генераллейтенанты артиллерии М.Ф.Васильев и К.К.Снитко, генерал-майоры И.П. Граве, В.Е.Слухоцкий, Д.А.Вентцель, М.Е.Серебряков, баллистики И.С.Шапиро, Б.Н.Окунев, А.А.Таскин и др. 1.3 Сведения из истории развития теории стрельбы Теория стрельбы артиллерии и стрелкового оружия, как и целый ряд проблем естественных наук, связанных с изучением закономерностей случайных массовых явлений, основывается на выводах теории вероятностей. Поэтому история развития теории стрельбы начинается с истории развития теории вероятностей. Возникновение теории вероятностей относится к XVII веку, однако первые задачи этой теории, как попытки обосновать распространенные в то время азартные игры, относятся к более раннему времени. Так, в XVI веке математики Д.Кардано, Н.Тарталья к другие пытались найти математические закономерности в появлении случайных результатов при метании игральных костей, игре в карты и т. п. В 1654 году было опубликовано сочинение известного математика Х.Гюйгенса «О расчетах в азартной игре», где был применен ряд математических методов, используемых в теории вероятностей. Подобными 15 вопросами занимались и такие видные математики XVII века, как Б.Паскаль и П.Ферма. Первыми учеными в России, занимавшимися вопросами теории вероятностей и ошибок наблюдений, были члены Петербургской академии наук Д.Бернулли и Л.Эйлер. Эйлер первый применил выводы теории вероятностей не только к азартным играм, но и к вопросам демографии и страхования. Первый курс теории вероятностей в России был прочитан профессором В.А.Анкудовичем в 1837 году в Петербургском университете, а в 1846 году академиком В.Я.Буняковским был написан первый русский учебник по теории вероятностей. Вопросами теории вероятностей занимались и такие корифеи русской математической науки, как Н.И.Лобачевский и М.В.Остроградский. В 1858 - 1859 гг., будучи профессором Михайловской артиллерийской академии, М.В. Остроградский впервые в академии прочел факультативный курс теории вероятностей. Новый этап в развитии теории вероятностей всецело связан с деятельностью гениального русского математика П.Л.Чебышева (1821-1894 гг.). Его заслуга заключается в том, что он впервые в мире придал теории вероятностей лицо настоящей науки. Чебышев дал доказательство основных законов теории вероятностей. Чебышев ввел в теорию вероятностей понятие случайной величины и ее математического ожидания. Большая заслуга Чебышева состоит в том, что он воспитал плеяду замечательных математиков, среди которых наиболее выдающимися были А.А.Марков и А.М.Ляпунов, с успехом продолжавшие и развивавшие идеи Чебышева. Широко развивавшееся в конце ХIХ века и особенно в начале ХХ века естествознание и техника все больше и больше используют выводы теории вероятностей и толкают ее на дальнейшие исследования. Теория вероятностей находит применение в самых разнообразных отраслях науки и техники: в молекулярной физике, астрономии, в математической и прикладной статистике, страховом деле, телефонии, контроле качества выпускаемой продукции, организации процесса производства, теории стрельбы и т. д. Применение в России теории вероятностей к вопросам стрельбы впервые ввел Н.В.Майевский в прочитанном им в 1858 году «Курсе баллистики». Однако уровень сведений из теории вероятностей в этом курсе был еще невысок. Коренной перелом в развитии теории стрельбы наступил после опубликования П.Л.Чебышевым своей работы «О средних величинах» (1867 год). В вышедшем в 1870 году «Курсе внешней баллистики» Н.В.Майевского вопросы применения теории вероятностей к стрельбе заняли уже более значительное место. В 1874 году в России выходит «Руководство в стрельбе из артиллерийских орудий», фактически ставшее первыми правилами стрельбы наземной артиллерии. Автором этого руководства был замечательный ученый артиллерист и популяризатор артиллерийских знаний В.Н.Шкляревич. Его расчеты, обосновывающие правила стрельбы, целиком базировались на теории вероятностей. 16 В 1882 году В.Н.Шкляревич в «Артиллерийском журнале» в многочисленных статьях развил и научно обосновал появившиеся в этом же году идеи капитана французской армии Персена и тем самым дал первую в мире теорию пристрелки. В 1895 году выходит в свет курс «Теория вероятностей и применение ее к стрельбе и пристрелке», автором которого был профессор Н.А.Забудский. После появления этого курса теория стрельбы выделяется из баллистики, как отдельная наука. С 1901 года в Артиллерийской академии читается самостоятельный курс теории стрельбы. Большой вклад в развитие теории вероятностей в теории стрельбы внесли советские ученые С.Н.Бернштейн, А.П.Колмогоров, А.Н.Хинчин, В.И.Романовский, Е.Е.Слуцкий, В.И.Гливенко, Н.В.Смирнов, Б.В.Гнеденко и др. Академики С.Н.Бернштейн и А.П.Колмогоров создали аксиоматическое построение теории вероятностей, благодаря чему теперь теория вероятностей представляет собой логически стройную математическую науку. Российские ученые не только развили и продолжили идеи школы Чебышева, но и внесли новые разделы в теорию вероятностей, они более тесно связали ее с другими математическими науками, впервые дали диалектикоматериалистическое обоснование теории вероятностей, проложив новые пути ее развития. Большое внимание российские ученые уделяют и различным приложениям теории вероятностей, в частности, вопросам теории стрельбы. Для подтверждения этого достаточно указать на работу академика А.Н. Колмогорова «Определение центра рассеивания и меры точности по ограниченному числу наблюдений» (1942 год), на участие академика А.П. Колмогорова и профессора В.И.Романовского в дискуссии по вопросу «О распределении цели» на страницах «Артиллерийского журнала» в 1950 году. Развитие теории стрельбы за годы советской власти продолжалось на новейшей научной основе. Уже в 1926 году в Артиллерийской академии были детально разработаны вопросы применения теории вероятностей к стрельбе, что позволило создать фундаментальные труды, на которых воспитывались крупнейшие советские артиллеристы, внесшие много ценного в развитие теории стрельбы. К числу видных представителей советской школы теории стрельбы относятся доктор военных наук генерал-майор артиллерии В.Г.Дьяконов, доктор технических наук генерал-майор инженерно-артиллерийской службы В.А.Алексеев, генерал-майор артиллерии П.М.Прохоров, доктор военных наук генерал-майор артиллерии Г.И.Блинов и др. В развитии теории стрельбы из стрелкового оружия выдающаяся заслуга принадлежит специалисту стрелкового дела Николаю Михайловичу Филатову (1860—1935 гг.). В 1897 году Н.М.Филатов издает свой первый труд «Записки по теории стрельбы» - пособие для слушателей Офицерской стрелковой школы. Это было первое пособие, написанное специально для стрелкового оружия с учетом всех его особенностей, с учетом того богатого опыта, который имела Офицерская стрелковая школа. 17 С появлением на вооружении станковых пулеметов Н.М.Филатов разрабатывает правила стрельбы для них. В этой работе вместе с ним участвовали крупнейший специалист по автоматическому оружию В.Г.Федоров и командир первой пулеметной роты С.А.Тихменев. После Октябрьской революции Н.М.Филатов, как начальник школы «Выстрел», а затем начальник Стрелково-Тактического Комитета, организует вокруг себя наиболее способных представителей стрелкового дела - М.В. Энвальда, С.А.Тихменева, В.В.Глазатова и др. Под руководством Филатова начинается детальная разработка правил стрельбы из станковых пулеметов, разрабатываются такие вопросы, как стрельба с закрытых позиций, стрельба в промежутки и поверх своих подразделений, стрельба по движущимся целям, стрельба по воздушным целям. Результаты этой работы отражены в капитальном труде Н.М.Филатова «Основания стрельбы из ружей и пулеметов», изданном в 1926 году, в ряде статей Н.М.Филатова и М.В.Энвальда, в книге С.А.Тихменева «Условия стрельбы по самолетам из станкового пулемета» и др. Эти и ряд других работ, проводившихся на Курсах «Выстрел» и в Стрелково-Тактическом Комитете, легли в основу правил стрельбы, вошедших в существующие наставления и руководства по стрелковому делу. Опыт Великой Отечественной войны и других вооруженных конфликтов показал, что российские воины, вооруженные лучшим в мире оружием и научно-обоснованными правилами стрельбы, способны решать любые боевые задачи [12]. Появление новых образцов современного вооружения требует от военнослужащих Российской Армии непрерывного совершенствования и развития правил стрельбы и способов боевого использования оружия. В решение этой серьезной задачи должны внести свой вклад инженеры по испытаниям, офицеры — руководители огневой подготовки. Помощь в этом им окажет теория стрельбы, сведения из которой излагаются в настоящем учебном пособии. 18 Глава II. Взрывчатые вещества 2.1. Взрывчатые вещества как источник энергии Взрывчатые вещества (ВВ) являются источником энергии, очень широко используемой в военном деле для различных целей — для метания снарядов (мин, пуль, гранат), для разрыва снарядов, для подрывных работ и т. д. Мощность, развиваемая при взрыве ВВ, чрезвычайно велика. Известно, например, что в современных артиллерийских системах ВВ, применяемые в качестве боевого заряда, позволяют метать снаряды весом в 300—500 кг на десятки километров; мощность, развиваемая при выстреле из такого орудия, составляет 204·105 квт. Мощность же взрыва 1 кг тротила составляет 748·105 квт. В ясный солнечный день на 1м² земной поверхности сосредотачивается столько солнечной энергии, что еѐ можно было бы использовать для приведения в действие мотора в 1 лошадиную силу. Однако прямым путем эту энергию еще не сумели использовать. Сейчас еѐ используют, только преобразуя в электрическую, накапливая в аккумуляторах. Растения усваивают солнечную энергию с коэффициентом полезного действия от 2 до 6%. Лучи солнца вызывают в растениях химическую реакцию, в которой участвуют вода и углекислота воздуха; образуются органические вещества растения. В результате процессов, длящихся сотни тысяч лет, растения превращаются в торф, уголь и другие виды топлива. При сжигании топливо вновь превращается в углекислоту и воду, а запасенная в нем солнечная энергия выделяется в виде тепла. Такое же сжигание, по существу, происходит и при взрывах. Если мы возьмем порошок того же торфа или угля и смешаем с жидким кислородом, то полученная смесь окажется очень мощным ВВ. Однако жидкий кислород чрезвычайно опасен в обращении, его обычно приходится химически связывать с топливом. Такое связывание кислорода с топливом имеет место почти во всех ВВ. Оно может быть осуществлено в виде механической смеси веществ, содержащих кислород и горючее топливо, или в виде химических соединений этих веществ. 2.2. Явление взрыва и виды взрывчатых превращений Взрывчатыми веществами называются такие вещества, которые при определенных условиях (трении, ударе и т. п.) быстро превращаются в большое количество сильно нагретых газов [19]. Взрывом называется явление быстрого физического или химического изменения вещества, сопровождающееся таким же быстрым превращением его потенциальной энергии в механическую работу [19]. Всякий взрыв характеризуется следующими признаками: Первый признак – скоротечность взрыва. 19 Время взрывчатого превращения практически применяемых количеств ВВ измеряется от сотых до миллионных долей секунды. Заряд 205-мм гаубицы сгорает примерно за 0,03 с, заряд 122-мм гаубицы примерно за 0,008 с, заряд патрона образца 1943 года за 0,0012 с, ВОГ-25 за 0,0023 с, подрывная шашка динамита весом в 400 г за 0,00001с [15, 19,40-42] (см. приложение №3). Скоротечность взрыва определяет огромную, по сравнению с другими источниками энергии, мощность ВВ. Так, например, мощность порохового заряда винтовочного патрона весом в 3,2 г составляет 13056 квт. Такую мощность имеют двигатели тяжелого бомбардировщика. При взрыве 1 кг динамита в течение 0,00002 с развивается мощность до 408·106 квт. Второй признак взрыва — образование большого количества газов. Количество выделяющихся при взрыве газов измеряется объемом, который они занимали бы при температуре 0ºС и давлении 760 мм ртутного столба. При взрыве различных ВВ газообразных продуктов образуется приблизительно в 900—1000 раз больше по объему, чем было вещества до взрыва. Отсюда понятны причины давлений при выстреле в канале ствола оружия — до 2000-4000 кг/см². Интересно напомнить, что давление в цилиндрах современных двигателей внутреннего сгорания составляет всего десятки кг/см². А в небольшом, размером со спичечную головку, кристаллике азида свинца при взрыве развивается давление в сотни тысяч атмосфер. Третий признак взрыва — выделение большого количества тепла. Так, при взрыве 1 кг ВВ выделяется от 500 до 1200 килокалорий тепла, при этом температура взрывчатого превращения достигает 2500° - 3500°С. Перечисленные выше факторы, характеризующие взрыв, могут иметь разные численные значения. В связи с количественным изменением этих факторов изменяется и качественная сторона явления взрыва. Особое влияние на качество оказывает скорость взрывчатого превращения. В зависимости от скорости реакции взрывчатого превращения различают три вида взрывов: быстрое горение, собственно взрыв и детонацию. Если скорость распространения реакции по массе ВВ не превышает несколько десятков метров в секунду, то давление газов при таком взрыве нарастает сравнительно медленно, газы производят работу по метанию окружающих тел. Примером такого взрыва, называемого быстрым горением, служит взрыв боевого заряда оружия. Если скорость распространения реакции по массе ВВ измеряется тысячами метров в секунду, то взрыв характеризуется резким нарастанием давления, ударом газов по окружающей среде, раскалыванием и дроблением окружающих предметов. Такой вид взрыва называют собственно взрывом. Возможен взрыв, при котором процесс разложения протекает с максимально возможной скоростью, измеряемой обычно тысячами м/с. Такой взрыв называется детонацией. Скорость детонации постоянна для каждого ВВ и определенных условий [17]. Например, скорость детонации пироксилина — до 6800 м/с, нитроглицерина — до 8200 м/с, гексогена — до 8400 м/с (см приложение №3). Характер действия при детонации — особенно резкий скачок давления и удар 20 газов с максимальным разрушительным эффектом. Явление детонации впервые было подмечено с нитроглицерином, когда он подрывался гремучей ртутью. Большинство ВВ в определенных условиях способно детонировать. Таким образом, скорость взрывчатого превращения является одной из всех характеристик, определяющих силу взрыва. Поэтому рассмотренные виды взрывчатых превращений предопределяют различия в боевом применении ВВ и являются основой для их классификации. 2.3. Классификация ВВ. Основные представители инициирующих и дробящих ВВ По боевому применению все ВВ делятся на четыре класса: инициирующие, дробящие, метательные и пиротехнические [19]. Инициирующими ВВ называются взрывчатые вещества, способные под действием начального импульса (удар, трение, сжатие, искра, пламя, нагрев) детонировать и вызывать воспламенение, взрыв или детонацию других ВВ. Инициирующие ВВ применяются для снаряжения капсюлей патронов, капсюльных втулок артиллерийских выстрелов и взрывателей к минам, снарядам и гранатам. Важнейшими представителями этой группы являются: гремучая ртуть, азид свинца, ТНРС, тетразен. Их характеристики приведены в таблицах №12, №14 (см. приложение № 1,3). Дробящими ВВ* называются взрывчатые вещества, основным видом взрывчатого превращения которых является детонация. Дробящие ВВ мало чувствительны к механическим воздействиям— трению, удару, прострелу пулей, но имеют хорошую восприимчивость к начальному импульсу от инициирующих ВВ. Это обеспечивает практическое удобство применения дробящих ВВ. Важнейшие представители дробящих ВВ и их характеристики приводятся в таблице № 13 (см. приложение № 2). Метательными ВВ (пороха) называются взрывчатые вещества, дающие взрывчатое превращение в виде быстрого горения. Сравнительно медленное нарастание давления при их горении позволяет использовать энергию горения для метания различных снарядов. Поэтому метательные ВВ применяют, главным образом, для изготовления боевых и холостых зарядов к огнестрельному оружию, ракетам и т. п. Метательные ВВ принято разделять на пороха, представляющие собой механические смеси и пороха коллоидного типа — химические соединения. По назначению (видам оружия) обычно пороха разделяются на четыре группы: Орудийные пороха. Пороха для стрелкового оружия. Минометные пороха. *Эти вещества называются также бризантными (от французского слова briser — дробить, разрушать). Ракетные пороха 21 Нитроцеллюлозные пороха (бездымные) в дальнейшем стали называться коллоидными. Пороха на летучем растворителе обычно называют пироксилиновыми порохами (в зарубежной литературе одноосновными). Применяются для винтовок, пистолетов. Пороха на труднолетучем и не летучем растворителе получили название баллиститов (в зарубежной литературе двухосновных). Используются для минометов, орудий и ракет. Пороха на смешанном растворителе, нитроглицериновые пороха на смешанном летучем и труднолетучем растворителе называются кордитами (для орудий и минометов). Пороха эмульсионного приготовления используются лишь как пороха для стрелкового оружия. Смесевые пороха – представляют собой гетерогенные системы, получаемые механическим смешением окислителей, горючих связующих веществ. Простейшим смесевым порохом является дымный. Смесевые пороха применяются в ракетах. В таких порохах окислителями являются нитраты и перхлораты. В качестве горюче связующих веществ используют высокомолекулярные вещества: каучуки, пластмассы, смолы и т. п. К первым относятся так называемые дымные пороха: дымный (черный) порох и аммонийный порох (селитро-угольные добавки). Дымный или черный порох представляет собой механическую смесь селитры, угля и серы. Селитра (KNO3) включает в себя кислородосодержащую группу, отдающую при взрыве кислород, необходимый для горения серы и угля. Сера, добавляемая к углю в качестве горючего вещества, играет роль цементирующего состава смеси и уменьшает гигроскопичность пороха. При взрыве черный порох дает около 47% твердых продуктов горения. Это явилось основной причиной замены его в боевых зарядах бездымными порохами. Сейчас черный порох применяется для изготовления воспламенителей к зарядам из порохов коллоидного типа, в вышибных зарядах шрапнелей, для осветительных и зажигательных снарядов в качестве горючего состава в огнепроводных шнурах, в дистанционных взрывателях и трубках. Аммонийный порох или селитро-угольные добавки. Недостаток сырья для изготовления бездымного пороха и стремление к удешевлению зарядов привели во время войны 1914 — 1918 гг. к применению суррогата бездымного пороха — к пороху из механической смеси аммиачной селитры и угля, называемому селитро-угольными добавками (СУД). Применяются они в военное время в боевых зарядах от 25 до 50% веса заряда взамен бездымного пороха. СУД близки по баллистическим свойствам к бездымному пороху и дают мало дыма при выстреле. Недостаток СУД — малая физическая стойкость (гигроскопичность, изменение структуры — вспучиваемость или слеживание) не позволяет применять этот порох в мирных условиях. Бездымные пороха — пороха, являющиеся химическими соединениями. 22 Основой всех бездымных порохов служит пироксилин (нитроклетчатка) — клетчатка*, обработанная азотной кислотой. В зависимости от природы растворителя, применяемого для дальнейшей обработки пироксилина, все бездымные пороха делят на две группы: пироксилиновые пороха, изготовляемые с применением летучего растворителя, который в дальнейшем почти полностью удаляется из пороха; нитроглицериновые пороха, изготовляемые на труднолетучем или нелетучем растворителе, полностью остающемся в порохе. Пироксилин, идущий на изготовление обоих видов бездымных порохов, получают, главным образом, из хлопка (содержащего до 92—93%клетчатки) или древесины (содержащей до 60% клетчатки), обработанных смесью азотной и серной кислот. В зависимости от наличия азота пироксилин разделяют на: - высокоазотный пироксилин № 1 (с содержанием азота от 12,9 до 13,3%), - низкоазотный пироксилин №2 (с содержанием азота от 11 до 12,3%). Эти виды пироксилина и используют для приготовления порохов. Пироксилиновый порох изготовляется из смеси пироксилинов № 1 и №2. Винтовочные пороха содержат по 50% каждого вида пироксилина, орудийные — 20% пироксилина № 1 и 80% пироксилина № 2. Пироксилиновая смесь обрабатывается летучим растворителем (спиртом и эфиром) и при застывании обращается в роговидную массу. Далее эта масса подвергается зернению, графитовке, укупорке и т. д. и порох обретает знакомую всем форму различного типа: цилиндров, пластинок, зерен, трубок. Такие пороха применяются сейчас в большинстве патронов стрелкового и артиллерийского оружия. Плотность (удельный вес) различных сортов пироксилинового пороха колеблется в пределах 1,54—1,63 кг/дм3. При хранении без герметической укупорки порох поглощает до 1,5% влаги, а при продолжительном хранении на открытом воздухе теряет часть растворителя. В результате этого изменяются баллистические качества пороха. Влажный порох может привести к неполному сгоранию боевого заряда и затяжному выстрелу. При уменьшенном количестве растворителя увеличивается скорость горения и повышается давление. Оба явления весьма нежелательны при стрельбе и должны быть исключены правильным хранением и обращением с боеприпасами. Нитроглицериновый порох изготовляется из пироксилина, растворѐнного нитроглицерином. Нитроглицерин (глицерин, обработанный смесью азотной и серной кислот) растворяет нитроклетчатку и является нелетучим растворителем. Нитроглицериновые пороха обычно содержат около 25% нитроглицерина, около 60—70% пироксилина и небольшое количество различных добавок. Нитроглицериновые пороха, изготовленные из пироксилина №1 (высокоазотного), называют кордитами; изготовленные из пироксилина №2 (низкоазотного) — баллиститами. Преимущества пироксилиновых порохов по сравнению с нитроглицериновыми выражаются в следующем: менее опасны в производстве; имеют *Клетчатка – это хлопок или древесина обработанные смесью азотной и серной кислоты. 23 более низкую температуру горения, что значительно увеличивает срок службы оружия. Преимущества нитроглицериновых порохов перед пироксилиновыми состоят в следующем: быстрота изготовления (до 10 часов вместо нескольких суток); низкая стоимость производства; более мощное действие, нежели пироксилиновый порох; большая физическая стойкость. Основным недостатком нитроглицериновых порохов является высокая температура взрывчатого превращения (3000ºС - 3500°С). Это ведет к значительному снижению срока службы оружия и делает применение нитроглицеринового пороха ограниченным. Однако в короткоствольных системах для получения большой начальной скорости применяются мощные пороха. В годы Великой Отечественной войны в нашей стране были разработаны нитроглицериновые пороха с более низкими температурами взрывчатого превращения, но эти пороха менее устойчивы при хранении, что допускает массовое их производство только во время войны. 2.3.1. Основные характеристики пороха Пороха обычно классифицируются по физико-химическим свойствам и баллистическим характеристикам. Физико-химические свойства порохов. Количество тепла, выделяемого при сгорании 1 кг пороха и при охлаждении газов до 15ºС (Q дж). Это одно из важнейших свойств, показывающее запас работы, сосредоточенный в 1 кг пороха. Для пироксилиновых порохов Q=376,83·104 дж, для нитроглицериновых Q=460,57·104 дж. Зная Q, легко найти потенциальную энергию пороха в килограммометрах: П=Q·427 кг·м. Объем газов при давлении 760 мм и температуре 0ºС, образовавшихся при взрыве 1 кг пороха (W дм3/кг). Это свойство имеет существенное значение при определении величин давления в канале ствола оружия при выстреле. Для пироксилиновых порохов W=900—970 дм3/кг, для нитроглицериновых несколько меньше — 800-860 дм³/кг. Температура горения (Т), т. е. температура, которую имеют пороховые газы в момент их образования. Пироксилиновые пороха имеют температуру горения Т=2200ºС-2500ºС, нитроглицериновые – 2700ºС-3200ºС. Баллистические характеристики порохов. Баллистическими характеристиками пороха называют величины, от которых зависят максимальное давление и скорость нарастания давления газов в канале ствола. 24 - «Сила» пороха (f кГ дм ) – работа, которую могли бы совершить газы кГ при сгорании 1 кг пороха. Наибольшей силой обладают нитроглицериновые кГ дм ; меньшей — пироксилиновые – около 8000 кГ кГ дм кГ дм и еще меньшей — дымные – 3000 [29]. кГ кГ пороха — около 11000 - Скорость горения пороха (u мм/с) при давлении 1 кг/см². Основное отличие пороха от бризантных ВВ способность гореть с конечной относительно большой скоростью параллельными или концентрическими слоями. Скорость горения (u) зависит главным образом от давления р и выражается формулой: где: u – скорость горения пороха (мм/с); u Apv , A – коэффициент; p – давление пороховых газов (кг/см2); v – показатель степени (для стрелкового оружия больше единицы, для артиллерийских систем меньше единицы). Для пироксилиновых порохов u=0,06-0,09 мм/с; для нитроглицериновых u=0,08—0,15 мм/с при давлении р=1кг/см2. При увеличении давления скорость горения возрастает примерно пропорционально давлению. Так, при давлении в 2000 кг/см² для пироксилиновых порохов u=0,09·2000=180 мм/с. При применении уравнения состояния в области внутренней баллистики необходимо учитывать объем молекул газов, выделяемых при сгорании 1 кг пороха, обозначенный αк (коволюм). Конкретный объем выделяемых газов выражается, следовательно, как αк·m и далее вычитается из общего объема V, т.е. появляется уточненное уравнение состояния для внутренней баллистики: p(V-αк·m)=mRT, где: Т – температура газов (К); R - метрический размер пороха. Чтобы получить αк, принята следующая зависимость для бездымных пироксилиновых порохов αк = (1381-0,557·Qω)·10ˉ³, где Qω = 775 дм³/кг (из таб. 1.2 средних значений физико-химических характеристик порохов [35]). Введем это значение в формулу αк = (1381-0,557·Qω)·10ˉ³=(1381-0,557·775дм³/кг)·10ˉ³=0,949 дм³/кг. Величины f и αк (см. табл. 1) определяются экспериментальным путем при подрыве манометрических бомб* с различной плотностью зарядов. Приведенные выше, а также некоторые другие характеристики порохов дают возможность производить расчеты, связанные с конструированием *Манометрическая бомба – прочный сосуд для снятия характеристик при подрыве ВВ 25 оружия (определение величины заряда, длины и толщины стенок ствола) и решением задач энергетических характеристик порохов внутренней баллистики. Таблица 1. Значение αк и f для некоторых порохов. Порох Черный порох Нитроцеллюлозный Нитроглицериновый Дигликолевый αк м³/кг 0,5·10ˉ³ (0,9…1.1) ·10ˉ³ (0,75…0,85)·10ˉ³ 1·10ˉ³ f Дж/кг (28…30)·104 (84…105)·104 (90…120)·104 100,5·104 2.4. Законы горения пороха Чтобы горение пороха началось, необходимо нагреть хотя бы не- большую часть его до температуры воспламенения, т. е. зажечь его. После этого выделяется количество тепла, необходимое для поддержания горения. Дымные пороха воспламеняются на открытом воздухе при температуре 270ºС — 320ºС; бездымные – при температуре около 200ºС. Момент, когда пороху сообщен такой начальный импульс, при котором он загорелся хотя бы в одной точке, называют зажжением. Далее в горении выделяют момент воспламенения, когда пламя распространяется по поверхности зерна. Распространение пламени вглубь зерна называют собственно горением. При исследовании свойств бездымных порохов и условий их горения было установлено, что при одинаковых по форме и размеру зернах порохового заряда и при условии, что масса пороха однородна во всех направлениях, горение пороха происходит по так называемому геометрическому закону. Положения этого закона горения следующие: • воспламенение пороха в замкнутом объеме происходит мгновенно; • горение бездымных порохов идет параллельными слоями с одинаковой со всех сторон скоростью. Установление этих закономерностей позволило внутренней баллистике производить теоретически все расчеты, связанные с использованием порохов. Однако практика показала, что при высоких давлениях в современном оружии геометрический закон описывает процесс не достаточно полно. Видный советский баллистик профессор М.Е.Серебряков установил действительный физический закон горения [30]. Этот закон можно свести к следующему: • масса пороха неоднородна от слоя к слою, и наружные слои горят с большей скоростью, чем внутренние; • характер зависит не только от формы пороховых зерен, но и от их взаиморасположения: чем ближе горящие поверхности расположены друг к другу, тем интенсивнее идет горение; 26 • в порохах с узкими и длинными каналами повышается давление газов и скорость горения увеличивается. Вскрытие этих закономерностей и установление численных зависимостей скорости горения пороха и образования пороховых газов от различных факторов позволяет в настоящее время полностью прогнозировать явление выстрела, т.е. строго рассчитывать, какой порох по физико-химическим и баллистическим качествам и в какой форме наиболее целесообразен для боевого заряда. 2.5. Форма и маркировка порохов Законы горения порохов устанавливают, что количество пороховых газов и быстрота газообразования для одних и тех же порохов зависят от формы и размеров пороховых зерен. Основным фактором, влияющим на скорость нарастания давления газов при выстреле, является характер изменения площади поверхности порохового зерна. Если при горении пороха в каждую последующую единицу времени горящая поверхность зерна уменьшается, то горение пороха называется дигрессивным. При его горении в каждую последующую долю времени образуется все меньшее количество газов. К таким порохам относятся заряды пистолетных, карабинных и винтовочных патронов, зерна которых имеют форму пластинок, а также пороха в форме лент, куба, прямоугольника, трубки (рис. 1а), сферические (рис.1в). Поэтому пороха подразделяются в зависимости от формы на дигрессивные и прогрессивные (многоканальные для увеличения площади горения). Если при горении пороха в каждую последующую единицу времени горения поверхность зерна остается постоянной, то горение называют постоянным. В каждую последующую долю времени при этом образуется почти одинаковое количество газов. Примером такого пороха могут явиться зерна трубчатой формы с одним каналом (рис. 1а). 2е1 а) 2е1 2е1 2е1 б) в) Рис. 1. Формы порохов: а) дигрессивного горения, б) прогрессивного горения, в) сферические, где: 2е1 – толщина горящего свода. 27 Такую форму имеет, например, порох 7,62-мм патрона и зарядов многих пушечных систем. При горении такого зерна внешняя поверхность уменьшается, а внутренняя соответственно увеличивается, и приток газов получается примерно постоянным (рис. 2б). Рис. 2. Схематическое изображение горения порохов: а) с семью каналами; б) с одним каналом. Если при горении пороха в каждую последующую единицу времени горящая поверхность зерна увеличивается, то горение называется прогрессивным. В каждую последующую долю времени при этом образуется большее количество газов. Примером такого пороха может явиться зерно в форме многоканальной трубки (рис. 1б). Такую форму имеет порох 14,5-мм патрона, гаубичных зарядов и зарядов некоторых пушек. При горении такого зерна поверхность горения увеличивается до момента распада трубки на частицы неправильной формы, которые уже догорают дигрессивно (рис. 2а). Прогрессивно горящий порох обеспечивает наиболее рациональное использование энергии боевого заряда при выстреле, так как дает возможность получить наибольшую начальную скорость снаряда при наименьшем максимальном давлении газов в стволе. Увеличение прогрессивности пороха может достигаться: • рациональным подбором геометрической формы порохового зерна (трубка с 7-ю каналами дает, например, на 80% прогрессивное горение); • флегматизацией пороха, т. е. введением в наружные слои зерна веществ, замедляющих горение и некоторыми другими мерами. Применение той или иной формы пороха зависит от вида огнестрельного оружия и его конструктивных особенностей. Форма порохов, применяемых для огнестрельного оружия, в большей мере зависит от длины ствола. Для длинноствольного оружия (пушки, винтовки, пулеметы) применяются флегматизированные пироксилиновые пороха цилиндрической формы с одним или несколькими каналами. Для короткоствольного оружия (пистолеты, пистолеты-пулеметы) применяются тонкие пластинки, обеспечивающие быстрое горение и создание в короткий промежуток времени 28 резкого нарастания давления. Для минометов употребляют также пластинчатые нитроглицериновые пороха. От формы и размеров пороховых зерен зависит такая важная характеристика боевых зарядов, как плотность заряжания. Плотностью заряжания (Δ) называют отношение веса заряда к объему, в котором происходит горение [20]. Плотность заряжания при современных формах порохов доходит до 0,95 кг/дм³. При увеличении плотности заряжания повышается скорость горения пороха, вплоть до возникновения детонации. Т. е. давление Р становится функцией плотности заряжания. В таблице 2 приведены некоторые значения Δ. Таблица 2. Плотности заряжания [43] Виды оружия Δ кг/дм³ 0,03...0,2 0,2...0,5 0,4...0,6 0,3...0,6 0,6...0,8 Гранатомѐты Гаубицы (уменьшенный заряд) Гаубицы (полный заряд) Танковые пушки Пушки (большой дальности стрельбы) Маркировка порохов. Порох, подобранный к определенному виду оружия, обозначают системой условных знаков — маркой. Марка пороха — условное обозначение, указывающее его баллистические свойства, состав, номер заводской партии, год изготовления и завод. Состав порохов обозначается следующим образом: • СВ — порох из свежего пироксилина; • СТ — порох, обновленный введением стабилизатора, без переделки, путем пропитывания в спиртовом растворе; • Пер — порох, переделанный из старых порохов; • НГВ — нитроглицериновый порох с примесью вазелина; • Н — нитроглицериновый порох последних лет изготовления; • НБ — нитроглицериновый порох измененного состава; • БСК — беспламенный порох с добавками; • ПГП — пламегасящий порох. Пороха пластинчатой формы обозначают буквами «Пл» и двумя числами, написанными через черточку. Первое число указывает толщину пластинки в сотых долях миллиметра, а второе — ширину ее в десятых долях миллиметра. Например, Пл-10-12, это означает, что порох пластинчатый, толщиной 0,1 мм и шириной 1,2 мм. Винтовочные пороха обозначают буквой «В». Если порох предназначается под тяжелую пулю, то добавляется буква «Т» (ВТ); если под легкую— «Л » (ВЛ). Порох для холостых зарядов обозначается буквой «Х». Трубчатые пороха обозначаются простой дробью, например, 1/7; 4/1; 7/1, где числитель – толщина горящего свода (расстояние между каналами) в 29 десятых долях миллиметра (0,1мм; 0,4мм; 0,7 мм); знаменатель — число каналов. Партия пороха и год изготовления обозначаются дробью: 5 6 ; , где числитель—партия пороха; знаменатель—год изготовле83 99 ния. Название завода обозначается одной заглавной буквой. Примеры маркировки пороха: Вл 14 К — винтовочный для легкой пули, 14 партия, 1999 год изготовле99 ния, К-ский завод; 7/7 3 П - орудийный семиканальный порох с толщиной свода 0,7 мм, 02 3 партия, 2002 года изготовления, П-ский завод. 30 Глава III. Сведения из внутренней баллистики. Баллистика—наука о движении снарядов [15]. Как и всякая наука, баллистика выросла на основе практической деятельности человека. Уже в первобытном обществе в связи с потребностями охоты люди накопили целый комплекс знаний о метании камней, копьев и дротиков. Наивысшим достижением того периода был бумеранг, сравнительно сложное орудие, которое после броска или поражало цель, или, в случае промаха, возвращалось назад к охотнику. Начиная с периода, когда охота перестала быть основным средством добывания пищи, вопросы метания тех или иных «снарядов» стали развиваться в связи с потребностями ведения войны. К этому периоду относится появление катапульт и баллист. Основное развитие баллистика, как наука, получила в результате появления огнестрельного оружия, опираясь на достижения ряда других наук: физики, химии, математики, метеорологии, аэродинамики и т. д. В настоящее время в баллистике можно выделить четыре части: • внутреннюю, изучающую движение снаряда под действием пороховых газов, а также все явления, сопровождающие это движение; • внешнюю, изучающую движение снаряда по прекращении действия на него пороховых газов; • раневую, дисциплина, составляющая сведения о процессах вызванных взаимодействием огнестрельного снаряда с живым организмом и о последствиях такого взаимодействия [50]; • конечную, изучающую конечное движение снаряда в преграде. 3.1. Предмет и задачи внутренней баллистики Внутренняя баллистика изучает явления, происходящие в канале ствола оружия во время выстрела, движение снаряда по каналу ствола и характер нарастания скорости снаряда как внутри канала ствола, так и в период последействия газов [8]. Важнейшей частью в явлении выстрела является порох боевого заряда, образующий газы, двигающие всю систему: снаряд — пороховые газы — ствол. Внутренняя баллистика занимается исследованием вопросов наиболее рационального использования энергии порохового заряда во время выстрела. Решение этого вопроса и составляет основную задачу внутренней баллистики: как снаряду данного веса и калибра сообщить определенную начальную скорость (V0) при условии, чтобы максимальное давление газов в стволе (Рm) не превышало заданной величины. Решение основной задачи внутренней баллистики делится на две части: • первая задача - вывести математические зависимости горения пороха; • вторая задача - рассчитать данные для проектирования оружия (конструктивные данные ствола и патронника). 31 Кроме этих двух общих задач, внутренняя баллистика решает много специальных задач: • расчѐт баллистического подобия артиллерийских систем (баллистически подобными называются системы, имеющие геометрически подобные кривые изменения давления газов и скорости снаряда); • исследование явления выстрела при смешанных* или комбинированных♦ зарядах; • исследование явления выстрела в ствольных артиллерийских системах; • исследование явления выстрела в реактивных системах и др. Внутренняя баллистика тесно связана с рядом смежных дисциплин: термодинамикой, механикой, математикой. 3.2. Сущность явления выстрела. Периоды выстрела Выстрелом называется выбрасывание снаряда из канала ствола давлением газов, образующихся при сгорании порохового заряда [10]. При выстреле из стрелковых и артиллерийских систем различают следующие основные процессы. Эти процессы взаимосвязаны и протекают одновременно, но мы их разделяем. Горение пороха и образование газов (в этом процессе скорость горения зависит в основном от природы и температуры пороха, от давления газов). Преобразование потенциальной энергии пороховых газов в кинетическую энергию движения системы. Движение газов заряда, снаряда и ствола. Несмотря на высокую интенсивность протекающих при выстреле процессов, они тем не менее закономерны, в определенных пределах управляемы и при сохранении одних и тех же условий заряжания стабильны от выстрела к выстрелу. В баллистике выстрел рассматривается как процесс очень быстрого превращения потенциальной энергии пороха в кинетическую энергию движения оружия (под оружием понимается система: пороховые газы - снаряд - ствол). Существенной особенностью выстрела является то, что работа пороховых газов по перемещению снаряда происходит в переменном объеме [18 - 23, 29]. Все эти особенности чрезвычайно осложняют исследование явления выстрела и чтобы получить общую картину явления, приходится рассматривать его по частям. Поэтому весь комплекс процессов, происходящих при выстреле, внутренняя баллистика разделяет на ряд отдельных вопросов, а само явление выстрела делится на четыре периода: предварительный, первый, второй и период последействия газов (рис. 3). * Смешанные заряды – заряды, составленные из различных марок порохов .♦ Комбинированные заряды – заряды, составленные из смеси ВВ. Например порох и тротил. 32 Рассмотрим эти периоды более подробно. Рис. 3. Периоды выстрела (кривые изменения давления газов и скорости снаряда даны в зависимости от времени). От удара бойка ударный состав капсюля воспламеняется, образовавшиеся газы, создающие первоначальное давление около 20 - 40 кг/см² и зажигают пороховой заряд. Во время горения порохового заряда образуется большое количество сильно нагретых газов. В дальнейшем все действия рассматриваем для боеприпасов с гильзовым заряжанием. Газы распространяются во все стороны и, стремясь расшириться, давят на снаряд, стенки и дно гильзы. Давление на дно гильзы заставляет ее прижиматься к затвору; давление на стенки гильзы плотно прижимает ее к стенкам патронника, предотвращая прорыв газов назад, давление на снаряд заставляет его двигаться по каналу ствола. Предварительный или пиростатический период – от момента начала воспламенения заряда до момента врезания снаряда (пули) в нарезы ствола. В некоторой литературе этот период делят на два [23, 27, 28]: I) Предварительный или пиростатический период – от момента начала воспламенения заряда до момента начала движения снаряда. II) Период форсирования – от момента начала движения до окончания врезания ведущих поясков снаряда (пули) в нарезы. В данном периоде горение пороха происходит в постоянном объеме, пока давление не достигнет величины, необходимой для страгивания снаряда. Это давление называют давлением форсирования (Рф). Давление форсирования 33 колеблется в пределах от 250—500 кг/дм² для снарядов и около 300—500 кг/дм² для пуль (в зависимости от твердости оболочки). Например, величина давления форсирования у 122-мм гаубицы обр. 1938 г. достигает 400 кг/дм², у стрелкового оружия под патрон обр. 1943г. - Рф=300 кг/дм², у выстрела ВОГ-25 – Рф= 50 кг/дм². Первый период или основной (Пиродинамический период) – от момента окончания врезания ведущих поясков до момента окончания горения пороха. Давление пороховых газов сначала быстро нарастает в увеличивающемся объеме, а затем, пройдя максимум, падает, скорость снаряда в этот момент составляет (0,8-0,9) Vд. В течение периода газы совершают большую часть работы. В этом периоде горение пороха происходит в быстро изменяющемся объеме, так как снаряд под давлением непрерывно возрастающего количества газов движется по каналу ствола. В первый промежуток времени нарастание количества газов идет значительно быстрее увеличения объема за снарядного пространства, поэтому и давление быстро повышается, достигая наибольшей величины, максимума (Рm). Например, при табличных условиях стрельбы максимальное давление, возникающее в стволе 122-мм гаубицы обр. 1938 г. Рmax =2350 кг/дм²; у стрелкового оружия под патрон обр. 1943 г. Рmax =2810 кг/дм², а под патрон с пулей обр. 1908 г. Рmax - 2850 кг/дм², выстрел ВОГ-25б* Pmax ≈ 1000 кг/дм2. Максимальное давление при выстреле из стрелкового оружия развивается при прохождении пулей 4 - 6 см пути, а в артиллерийских системах при прохождении снарядом 20 - 45 см. Однако быстрое увеличение давления вызывает значительное ускорение движения снаряда в канале ствола, т. е. значительное увеличение за снарядного пространства. Поэтому, несмотря на приток новых газов, давление начинает падать до конца горения пороха (Рк), а скорость снаряда все время возрастает, достигая значения Vк. Второй или термодинамический период – от момента окончания горения порохового заряда до момента вылета из канала ствола. Давление газов падает, скорость снаряда достигает скорости Vд. С началом этого периода приток новых газов прекращается, но так как газы обладают большим запасом энергии, то продолжается их расширение и, как следствие этого, увеличение скорости движения снаряда. В этот период давление убывает от Рк до дульного Рд. Величина дульного давления у различных образцов оружия колеблется в пределах 300 - 600 кг/см². Например, у карабина Симонова и ручного пулемета Дегтярева - Рд=390 кг/см2, у пулемета Горюнова - 570 кг/см2, у 76-мм дивизионной пушки около 600 кг/см2, выстрел ВОГ-25б - Pk =988,6 кг/см2. Скорость снаряда у дульного среза может быть меньше табличной начальной скорости. В стрелковом оружии полное сгорание порохового заряда происходит к тому моменту, когда пуля находится вблизи дульного среза, а в системах с * ВОГ-25б – бесшумный выстрел. 34 более коротким стволом (например, пистолет) полного сгорания пороха не происходит, т. е. второй период выстрела фактически отсутствует. Третий период или период последействия – от момента вылета снаряда из ствола до момента окончания последействия истекающих из ствола пороховых газов. В конце этого периода снаряд получает максимальную скорость Vmax или V 0 . Период последействия заканчивается при падении давления в канале ствола примерно 1 кг/см². Этот последний период выстрела характеризуется тем, что газы, истекающие из ствола вслед за снарядом обгоняя его, продолжают действовать на него. Их скорость в момент истечения достигает 1100 – 1400 м/с. Длина участка последействия у стрелкового оружия достигает нескольких десятков сантиметров, а у некоторых артиллерийских систем до нескольких метров. Для некоторых видов оружия, особенно короткоствольного, например, пистолетов, из-за короткого ствола второй и третий период объединяются в один. То есть порох не успевает полностью сгореть в стволе и частицы пороха догорают в воздухе. Для боеприпасов с отсечкой пороховых газов остаются в силе только два с половиной периода [40, 42]. А именно: 1) Предварительный период. 2) Первый или основной. 3) Частично второй. Рис. 4. Патрон СП-3 Предварительный период остается таким же, как и у всех видов боеприпасов. Первый период протекает до момента полного сгорания пороха, часть второго периода, когда порох сгорел, поршень продолжает движение до полного раскрытия цилиндра. Пуля продолжает движение по стволу за счет приданной энергии. В некоторых случаях порох в первом периоде не сгорает, а поршень останавливается. Догорание пороха происходит в постоянном объеме. В данном случае второй период отсутствует. Пуля продолжает движение по стволу за счет приданной энергии (см. рис.4). На примере графиков P (l), Р (t) (рис.5), рассмотрим работу телескопического боеприпаса с отсечкой пороховых газов [40,42]. На первой стадии мы видим резкое повышение давления до достижения максимума, а потом резкий спад. На второй стадии также небол ьшой спад. На третьей - уже небольшой рост давления, видимо 35 увеличения объѐма при выдвижении поршня не хватает для пон ижения давления и происходит его возрастание. Р·104 (кГ/см2) Рmax=1000 кГ/см2 620 кГ/см2 Рmax=1000 кГ/см2 Р·104 (кГ/см2) 980 кГ/см2 Рис. 5 Графики зависимостей: P (l), P (t). На четвѐртой стадии все штоки выдвинулись, объѐм постоянный, а порох продолжает гореть и давление возрастает, пока весь порох не сгорит. В итоге давление достигает отметки 980 кг/см2. Образование звуковой волны. Раскаленные пороховые газы, истекающие из ствола вслед за снарядом, при встрече с воздухом вызывают ударную волну, которая является источником звука выстрела. Смешивание раскаленных пороховых газов с кислородом воздуха вызывает вспышку, наблюдаемую как пламя выстрела. Звук выстрела, порождаемый дульной волной — основная составляющая «шумности» любого огнестрельного оружия — объясняется высокими давле36 нием и температурой пороховых газов у дульного среза, намного превосходящими давление и температуру окружающего воздуха. Быстрое расширение пороховых газов после вылета из ствола, сменяющееся разрежением, в силу упругости воздуха создает дульную ударную волну и сопровождается резким и громким звуком, распространяющимся по всем направлениям. Особенно резок звук выстрела в начальной фазе возбуждения дульной волны. При дозвуковой скорости пули При сверхзвуковой скорости пули Рис. 6. Образование при выстреле дульной и баллистической звуковых волн. 1ствол;2-пуля; 3-дульная волна. Таким образом, явление, происходящее при выстреле, характеризуется увеличением давления до Рm , затем падением давления от Pm до Pд и далее до атмосферного и возрастанием скорости от 0 до Vm. Характер изменения давления газов и скорости снаряда в канале ствола обычно изображают в виде графика, где по горизонтальной оси откладывают в масштабе отрезки пути, пройденного снарядом в стволе, или время, затраченное на разгон, достижение давления. По вертикали — величину давления или скорости (рис.7). Данные о величинах давления и скорости на каждом участке получают стволстводульная волна. расчетным путем при решении основной задачи внутренней баллистики, а после создания опытного образца оружия— специальными приборами. Деление явления выстрела на рассмотренные периоды основывается на возможности для каждого отдельного периода производить математические расчеты величин давления газов и скорости снаряда. Так, в предварительном периоде, когда горение происходит в постоянном объеме, расчеты производятся по формулам пиростатики. Пиростатика — раздел внутренней баллистики, изучающий законы горения пороха, образование газов и развитие давления при неподвижном снаряде. В первом периоде расчеты производятся по формулам, учитывающим горение пороха в изменяющемся объеме, а во втором периоде величина давления газов и скорости снаряда определяется по формулам свободного расширения 37 газов. Эти два периода входят в раздел баллистики, называемый пиродинамикой. Пиродинамика — раздел баллистики, изучающий законы газообразования и возникновения движения снаряда с учетом охлаждения газов и совершения механических работ. Период последействия изучается разделом внутренней баллистики— газодинамикой. Газодинамика изучает явления, связанные с движением и истечением газов в период последействия, а также истечения их через сопло реактивных снарядов, через отверстия дульных тормозов и пр. 3.3. Прочность и живучесть ствола. Действие нагара на ствол оружия При выстреле давление газов в стволе оружия достигает очень больших величин, поэтому устройство ствола должно обеспечивать достаточную его прочность. Под прочностью понимается способность ствола выдерживать определенное давление без остаточной деформации. Из графика (рис.7) видно, что нет смысла весь ствол рассчитывать на максимальное давление газов, так как по мере продвижения снаряда вперед давление падает. Поэтому обычно в казенной части стенки более толстые, чем во всей остальной части ствола. В каждом сечении стенки ствола изготавливаются с запасом прочности, позволяющей выдерживать давление в 1,3 - 1,5 раза больше, чем давление, возникающее при выстреле. Рис. 7. График изменения давления газов и скорости снаряда в стволе в зависимости от пути 38 При всех величинах давления, на которые рассчитано оружие, ствол подвергается только упругим деформациям расширения; при воздействии давления ствол расширяется по окружности, а с прекращением давления принимает первоначальные размеры. Однако в процессе эксплуатации могут возникнуть условия, при которых давление в канале ствола может превосходить рассчитанный запас прочности. В этом случае ствол подвергается остаточной деформации, т. е., расширившись под действием газов, после прекращения давления не восстанавливает своих размеров. Такое явление называется раздутием ствола. В большинстве случаев раздутие, получается, от попадания в ствол посторонних предметов (пакли, тряпки, песка, земли и пр.). Снаряд, натыкаясь на посторонний предмет, замедляет свое движение. Газы, следующие за снарядом, отталкиваются от его дна и создают обратное движение. При столкновении газов, движущихся в противоположных направлениях, возникает скачок давления, превосходящий величину, на которую рассчитан ствол: происходит раздутие ствола, а иногда и разрыв его (рис. 8). Рис. 8. Скачок давления, вызвавший раздутие ствола. Оружие, имеющее раздутие ствола, непригодно к стрельбе. В целях предупреждения раздутия и разрывов необходимо тщательно протирать канал ствола, внимательно осматривать его перед каждой стрельбой, оберегать стволы при передвижениях от засорения, не допускать затыкания стволов 39 стрелкового оружия и обязательно снимать перед стрельбой дульные чехлы орудий и минометов. Высокое давление, возникающее в канале ствола при выстреле, требует полной надежности запирания его затвором, что обеспечивается определенной конструкцией оружия. Поэтому при стрельбе необходимо тщательно следить за работой узла запирания, так как случайный выстрел при не полностью закрытом затворе приводит к тяжелым последствиям. При длительной эксплуатации оружия, а также при недостаточно тщательной подготовке его к стрельбе может образоваться увеличенный зазор между зеркалом затвора и стволом. При выстреле этот зазор позволяет гильзе двигаться назад. Но стенки гильзы, расширившись под давлением газов, плотно прижаты к патроннику. Возникшие при этом силы трения препятствуют движению гильзы; гильза растягивается и, если зазор велик, рвется. Происходит так называемый поперечный разрыв гильз. Для того чтобы избежать разрывов гильз, необходимо при подготовке оружия к стрельбе проверять величину зазора, содержать патронник в чистоте и не применять для стрельбы загрязненные патроны, что может вызвать увеличение сил сцепления стенок гильз с патронником. Предотвращению поперечных разрывов гильз способствует протирание патронника и легкая смазка гильз ружейным маслом. Предельное число выстрелов, которое можно сделать из данного ствола до допустимой степени его износа, называется живучестью ствола (см. приложение №4). Основными признаками, по которым в практике можно судить о непригодности стволов, являются следующие. Для артиллерийских стволов — падение начальной скорости более, чем на 5% - 7% по сравнению с табличной. Падение начальной скорости в войсковых условиях определяется по удлинению зарядной каморы для раздельного заряжания способами, описанными в Руководствах службы. Для стрелкового оружия — увеличение рассеивания пуль до 2,5 раз по сравнению с табличным или появление срывов пуль с нарезов (свыше 50%), которые обнаруживаются наличием на мишени овальных пробоин. Для повышения живучести важно установить причины, вызывающие износ и разгар ствола. Их обычно объединяют в три группы. Причины механического характера (трения). Износ канала ствола под действием этих причин представляет собой изменение диаметра канала по нарезам и по полям, а также изменение профиля нарезки (рис. 9). При врезании снаряда в нарезы вследствие большого трения происходит их износ, который увеличивается с последующими выстрелами. Поля нарезов на расстоянии 3-6 калибров от начала нарезов при большом числе выстрелов совершено выкрашиваются и исчезают. Существенной причиной износа стволов, особенно стрелкового оружия, является механическое истирание ствола во время чистки при неправильном использовании принадлежности. 40 а б в Рис. 9. Изменение диаметра и профиля нарезки канала ствола после большого числа выстрелов: а) новый ствол, б) до предельного числа выстрелов, в) после большего числа выстрелов. Причины термического характера. Высокая температура пороховых газов сильно, но неодинаково нагревает слои стенок ствола. Вследствие кратковременности выстрела высокая температура успевает передаться лишь очень тонкому внутреннему слою, который, стремясь расшириться, встречает противодействие менее нагретых слоев металла. После выстрела наступает быстрое охлаждение внутреннего слоя, и он начинает сокращаться. Глубокие же слои, охлаждаясь значительно медленнее, будут задерживать это сжатие. Такое попеременное сжатие и расширение внутреннего слоя вызывает появление на нем сетки трещин (сетки разгара). Покрытый сеткой трещин поверхностный слой под действием пороховых газов постепенно выкрашивается, и частицы отколовшегося металла выносятся из канала ствола. Такая картина износа — с отколом мельчайших частиц хрома — особенно характерна для хромированных стволов стрелкового оружия. Причины химического характера. Износ ствола под действием этих причин представляет собой износ поверхности канала ствола под влиянием химического состава пороховых газов. Наличие окиси углерода и азота в продуктах разложения порохового заряда вызывает цементацию и нитрирование стенок ствола, придающие поверхностному слою большую хрупкость. Большое влияние на износ ствола оказывает образующийся при выстреле нагар. Количество нагара в стволе зависит от числа выстрелов и качественного состояния ствола. Чем больше произведено выстрелов и чем хуже состояние ствола, тем больше в нем остается нагара. Например, после ста выстрелов из винтовки в стволе, не пораженном сыпью, остается около 0,06 г нагара; в стволе, пораженном сыпью и раковинами, - 0,22 г, т. е. почти в 4 раза больше. Нагар состоит из растворимых (12 - 25 %) и нерастворимых веществ (68 75%). Растворимые вещества представляют собой соли, образующиеся при сгорании капсюльного состава, в основном, хлористый калий (КСl). Нерастворимыми частями нагара являются: томпак, сорванный с оболочки пули; медь, латунь, оплавленные из гильзы; свинец, выплавленный из дна 41 пули; олово из расплавленной фольги, прикрывающей капсюль; железо, оплавленное из ствола и сорванное с пули; зола, образовавшаяся при сгорании порохового заряда. Наиболее вредной примесью растворимых солей нагара является хлористый калий. Эта соль плавится при температуре 768ºС и обращается в пар при 1415ºС. Во время выстрела, когда температура достигает 2800ºС, хлористый калий в виде пара находится в пороховых газах. Соприкасаясь с холодными стенками ствола, пары хлористого калия конденсируются и в виде расплавленной соли или мелких кристалликов покрывают поверхность ствола. При этом стальная поверхность канала ствола нагревается и частички хлористого калия приплавляются к ней, образуя блестящий, стекловидный слой. Калиевые соли пропитывают все остальные частицы рыхлого нагара, как бы цементируют их, превращая из легко удаляемой массы в твердое, трудно сдираемое вещество, плотно приклеившееся к поверхности металла. Содержащиеся в нагаре соли легко впитывают влагу из атмосферного воздуха и превращаются в насыщенные растворы солей, вызывающие усиленное ржавление металла. (Напомним, что один литр воздуха, считающегося сухим, при температуре 20ºС содержит около 10 миллиграммов воды). На рис. 10 показана схема развития коррозии в канале ствола винтовки, не вычищенной после стрельбы. До выстрела (рис.10а) поверхность канала ствола со всеми ее рисками, порами, трещинами покрыта тонким слоем смазки. После нескольких выстрелов смазка сгорает, поверхность канала ствола покрывается рыхлым слоем нагара, под которым к металлу приплавилась стекловидная корочка солей (рис.10б). На отдельных местах поверхности канала проплавляются частицы меди, сорванные с оболочки пули. После окончания стрельбы ствол остывает и происходит отпотевание металла, при котором соли нагара, поглощают влагу из воздуха, и образуется их насыщенный раствор (рис. 10 в). Так создаются благоприятные условия для ржавления. На поверхности канала ствола, особенно в местах углублений и трещин, образуются раковины, которые быстро увеличиваются в своих размерах. Особенно быстро образуются раковины в непосредственной близости от омедненных участков, так как медь и сталь, покрытые солями нагара, как электролитом, образуют гальванический элемент, где быстро разрушающимся отрицательным полюсом является сталь. Таким образом, износ внутренних стенок ствола является результатом действия многих причин и зависит как от химического и термического воздействия пороховых газов, так и от причин механического характера. Все эти причины вызывают изменение поверхности канала ствола и приводят к его расширению, особенно у дульного среза и у пульного входа, что ухудшает центрирование снаряда в стволе. Это приводит к значительному увеличению рассеивания, неправильности полета снаряда и уменьшению дальности стрельбы, сокращая общий срок службы ствола. 42 Рис. 10. Схема коррозии канала ствола винтовки, не вычищенной после стрельбы: а - до выстрела; б - после нескольких выстрелов; в - после отпотевания; г - после ржавления; д - после чистки ствола. Главной причиной износа оружейных не хромированных стволов является механическая реакция. Хромированные же стволы выходят из строя главным образом по причине сильного разгара с казенной части. Увеличения живучести стволов можно достигнуть: тщательной обработкой поверхности канала; применением легированных сталей; хромированием с целью увеличения твердости поверхности канала ствола; применением пороха с возможно меньшей температурой горения; применением неоржавляющего капсюльного состава; рациональная конструкция ведущих поясков и некоторыми другими мерами. В тоже время большое значение для живучести ствола имеет правильная его эксплуатация. Так как живучесть ствола сильно снижается при повышении температуры, 43 необходимо принимать меры по уменьшению нагрева стволов во время стрельбы. Количество выстрелов до полного износа ствола артиллерийского орудия зависит от мощности орудия, т.е. падением Pm, V0, Qтем , где: Pm - максимальное давление; V0 - начальная скорость; Qтем. - температура нагревания пороха. Для орудий средней мощности (полковой и дивизионной артиллерии) количество достигает 10000; для систем большой мощности - до 1000 и меньше (см. приложение 4). На износ ствола может влиять и масса снаряда, без изменения навески пороха. Так, например, при стрельбе из 125-мм орудия (Д-81) ОФС ресурс ствола – 350 выстрелов, а при стрельбе подкалиберным снарядом - 150 выстрелов. Данный пример наглядно показывает, как влияет изменение массы снаряда на износ ствола. Например, при стрельбе из 122-мм гаубицы только наименьшими зарядами живучесть ствола будет в несколько раз больше, чем при стрельбе только полными зарядами. Поэтому, если огневую задачу можно решить стрельбой при меньшем заряде, то ни в коем случае не следует применять заряды большего веса. Приведѐнное количество выстрелов – количество выстрелов эквивалентное стрельбе на полном заряде при нормальных условиях стрельбы ОФС. • 2 заряд (уменьшенный) - 1 выстрел равен 0,8 приведенных. • Усиленный заряд - 1 выстрел равен 1,3 приведенных. • Калиберный заряд - 1 выстрел равен 1,4 приведенных. На температуру и давление пороховых газов при выстреле сильно влияет температура заряда. С повышением температуры заряда, что происходит, например, при хранении зарядов на огневой позиции на солнцепеке, скорость горения заряда, наибольшее давление и температура газов в канале ствола увеличиваются, следовательно, ускоряются разгар и износ канала ствола. Этим объясняется требование к хранению зарядов артиллерийских выстрелов и патронам стрелкового оружия на позициях в тени, в нишах, под брезентом и т. п. Исключительно большое значение имеет соблюдение режима огня, установленного для данного вида оружия. Без особой надобности, не вызванной обстановкой боя, не следует вести излишне интенсивную стрельбу, особенно из автоматического оружия, так как высокий темп стрельбы приводит к сильному нагреву ствола. Живучесть ствола во многом зависит от ухода за ним, от своевременности его осмотра, чистки и смазки. Перед каждой стрельбой канал ствола следует тщательно протереть, удалив из него загустевшую смазку, пыль и посторонние предметы. Нужно также следить, чтобы канал ствола не загрязнялся от боеприпасов, для чего их перед заряжанием необходимо обтереть от смазки и тщательно осмотреть. Стрельба снарядами, имеющими забоины или ржавчину, особенно на центрующем утолщении, недопустима, так как она может привести к повреждению канала ствола. 44 Особое значение для сбережения стволов имеет своевременная и правильная чистка, и смазка оружия. Старый метод чистки требовал после стрельбы густой смазки канала ствола щелочным составом. Стволу «под щелочью» давали постоять от 2 до 4 часов. Предполагалось, что за это время «кислотные окклюдированные газы», выйдя из пор стальных стенок канала, будут нейтрализованы (обезврежены) щелочью, и ржавление будет устранено. Кроме того, щелочь размягчит (отъест) нагар, и он легче очистится. После этого оружие чистилось паклей той же щелочью до тех пор, пока на пакле не оставалось черноты, а в стволе заметна была только синева от металла. Затем канал ствола протирали насухо и смазывали ружейной смазкой. Если оружие вносилось с холода в теплое помещение, приступать к его чистке разрешалось только после того, как оно отпотеет и высохнет. В последующие дни чистка повторялась, и каждый раз тряпка после чистки покрывалась грязью. Только после трех - пяти чисток нагар удалялся. Тем не менее, через некоторое время канал ствола оказывался пораженным коррозией. Причиной этого является рассмотренное выше действие растворимых солей нагара от капсюльного состава. В последние годы правила чистки оружия, изложенные в наставлениях и руководствах по стрелковому делу, основываются на положениях новой теории коррозии оружия, разработанной В.Н.Поддубным. Они заключаются в следующем: • оружие необходимо чистить немедленно после стрельбы, по возможности на самом стрельбище; • весь нагар необходимо удалять при первой же чистке; • оружие следует чистить вторично для удаления нагара, который мог остаться в стволе, если первая чистка производилась в недостаточно удобных условиях (на стрельбище), вторичная чистка производится немедленно по приходу в места постоянной дислокации; • для стрелкового оружия, если ствол отпотел при внесении его после стрельбы с холода в теплое помещение, чистка производится немедленно, чтобы не дать оружию согреться, а капелькам росы высохнуть; • после чистки ствол протирается насухо и затем слегка смазывается. При правильном уходе за стволом можно избежать ржавления и, следовательно, образования сыпи и раковин. Правильный уход за оружием позволяет значительно повысить срок службы ствола. Живучесть стволов стрелкового оружия достигает 10 – 12 тысяч выстрелов, а хромированного - до 30 тысяч выстрелов (см. приложение № 3). Отсюда становится понятной важность строгого соблюдения режима огня, своевременной смены нагретых стволов и учета по формулярам общего числа выстрелов. Стволы крупнокалиберных пулеметов, где при выстреле Рm достигает 3050 кг/см² имеют меньшую живучесть. Так, у 14,5-мм крупнокалиберного пулемета после 1000 выстрелов начальная скорость падает. 45 3.4. Движение снаряда по каналу ствола Рассмотренная выше картина явления выстрела и некоторые выводы по сбережению оружия характеризовали лишь часть общего действия пороховых газов. Основная работа пороховых газов затрачивается, с одной стороны, на придание снаряду поступательного и вращательного движений, а с другой стороны - на отдачу оружия. Работа, затрачиваемая на сообщение снаряду поступательного и вращательного движения, составляет примерно 25-35% от полной энергии пороховых газов (эта величина является коэффициентом полезного действия оружия). Вращательное движение снаряда, необходимое для обеспечения устойчивости его полета в воздухе, достигается устройством нарезов в канале ствола (рис. 11). Длина хода нарезов, обеспечивающих устойчивость полета снаряда, вычисляется по определениям внешней баллистики. Так, для стрелкового оружия длина хода нарезов обычно колеблется от 30 до 37 калибров, для пушек – от 25 до 37 калибров, для гаубиц – от 25 до 32 калибров. Направление нарезов может быть правое и левое. В оружии Российской Армии принято правое направление - оно соответствует общепринятому в промышленности направлению резьбы в винтовых соединениях. Левое направление (например, в английском оружии) не имеет никаких преимуществ перед правой нарезкой [16, 44, 45]. Число нарезов определяется прочностью полей нареза боевых выступов ведущего пояска. В стрелковом оружии приняты четыре нареза, у крупнокалиберных пулеметов - восемь, у 30-мм автоматических пушек: 2А42, 2А72 – 16, у мощных артиллерийских орудий число нарезов доходит до 64 [1-8, 46,47]. Двигаясь по каналу ствола, снаряд (пуля) под действием давления пороховых газов врезается медным ведущим пояском (оболочкой) в нарезы и получает вращательное движение. Рис. 11. Вид и схема нарезов в канале ствола. Д—диаметр канала ствола, называемый калибром. 46 3.5. Начальная скорость снаряда Начальная скорость снаряда (V0) – это условная скорость в точке вылета, которая получается расчетным путем [8, 10]. Начальная скорость является одной из важнейших баллистических характеристик оружия, оказывающей влияние на его боевые свойства. При увеличении начальной скорости увеличиваются дальность полета снаряда, настильность траектории, поражаемое пространство, бронепробиваемость, а также уменьшается влияние внешних условий на полет снаряда. В таблицах стрельбы и наставлениях указываются величины начальных скоростей несколько большие, чем скорость снаряда в момент вылета (Vд). Объясняется это следующим образом. При движении снаряда по каналу ствола под действием пороховых газов скорость его все время увеличивается и достигает значения Vд. Если бы период последействия отсутствовал, то эта скорость была бы наибольшей, ею определялось бы начало движения снаряда в воздухе. Но во время периода последействия под давлением истекающих газов скорость снаряда продолжает еще несколько увеличиваться и достигает какого-то значения Vm (рис. 12), после которого начинает убывать. Участок периода последействия газов у оружия незначителен, поэтому считают, что снаряд после вылета из канала ствола не подвергается действию пороховых газов. Но в этом случае действительная скорость снаряда в момент вылета оказывается не связанной с кривой изменения скорости полета снаряда в воздухе. Рис. 12. Выбор начальной скорости. Для того, чтобы избежать такого разрыва, за начальную скорость принимается такая условная скорость в точке вылета, которая согласовывается с кривой скоростей снаряда за пределами участка последействия. Таким образом, начальная скорость определяется по закономерностям, характеризующим изменение скорости снаряда в воздухе. Следовательно, для определения начальной скорости необходимо определить скорость снаряда в 47 определенных точках в воздухе и затем полученную кривую построить до дульного среза. Для определения скорости снаряда в какой-либо точке в воздухе применяются специальные приборы – хронографы*. Сущность определения скорости снаряда при помощи хронографа заключается в следующем (рис. 13). На определенном расстоянии друг от друга устанавливаются две мишени, которые представляют собой либо деревянную раму с натянутой проволокой (для артиллерийских систем), либо наклеенную на бумагу фольговую мишень (поз. 1 и 2) (для стрелкового оружия), рассчитанную так, чтобы снаряд (поз. 3) обязательно при пробивании рамы перервал проволоку или фольговую полоску. При этом разъединяется электрическая цепь. Обе рамы-мишени соединены с хронографом. При пробивании снарядом поочередно первой и второй раммишеней хронограф дает возможность определить время полета снаряда между двумя рамами. Зная расстояние между рамами-мишенями, и принимая движение на этом участке равномерным, определяют среднюю скорость снаряда на участке между рамами-мишенями по формуле: Vср. S , t 2 1 3 S t хронограф Рис. 13. Принципиальная схема измерителя скорости. S – расстояние между мембранами; t – время между импульсами; 1 – первая мембрана; 2 – вторая мембрана; 3 - пуля. * Хронографами называются приборы, при помощи которых измеряется время движения снаряда с целью определения его скорости. 48 где Vср. - средняя скорость снаряда на участке между двумя рамами- мишенями; S - расстояние между рамами-мишенями; t - время полета снаряда между рамами-мишенями. Обычно расстояние между рамами-мишенями составляет 50 м, поэтому найденную среднюю скорость Vср. принимают за скорость снаряда в 25 м от дульного среза (V25). Пример. Первая рама-мишень установлена непосредственно у дульного среза пулемета ПКМ (обычно вместо первой рамы-мишени для стрелкового оружия применяется дульный хомутик с проволочкой прерывателем), вторая — стальная плита с инерционным прерывателем — в 50 м от дульного среза. Хронограф показал время t = 0,062 с. Тогда скорость снаряда в 25 м от дульного среза равна: V25=50:0,062=805 м/с. Зная скорость снаряда в данной точке и закон изменения скорости снаряда во время полета, при помощи соответствующих формул получают величину начальной скорости. Обычно определяют скорость снаряда в 25 м от дульного среза и умножают ее на величину 1,025, определенную при помощи формул для приведения к дульному срезу. Таким образом, V0 = 1,025·V25. Пример. Определить начальную скорость пули обр. 1908 г., выпущенной из пулемета ПКМ, если с помощью хронографа установлено, что скорость пули в 25 м от дульного среза равна 805 м/с. V= 1,025·V25 , V0 =1,025·805=825 м/с. По своему устройству хронографы имеются самых различных видов. Для стрелкового оружия широко применяется электромагнитный хронограф с падающим телом. Широкое распространение имеют также искровые и соленоидные хронографы. Принцип определения начальной скорости можно показать на простой установке в классе. Время полета пули на расстояние АБ (рис.14), например, в 10 м определяется по высоте падения фанерки (С), удерживаемой ниткой, которая через два ролика проведена к дульному срезу укрепленного в прицельный станок малокалиберного пистолета Марголина. Пуля при выстреле обрывает нить, заставляет фанерку С падать, затем пробивает ее, а также поставленный за ней неподвижный щит К. Положение фанерки С до выстрела было отмечено на щите К. Если теперь совместить пробоины на фанерке и неподвижном щите, то можно измерить величину свободного падения фанерки. При дальности стрельбы в 10 м 49 Рис. 14. Схема учебной установки для определения начальной скорости пули. фанерка успевает спуститься примерно на 10 мм. Зная путь падения h=10,0мм=0,01 м, найдем из выражения время полета пули t: h gt 2 ; 2 gt 2 t2 2h ; t 2 0,01 9,81 2h ; g t 2h ; g 0,045c. Средняя скорость пули на участке в 10 м равна V S ; V=10:0,045≈222 t м/с. В нашем опыте ее можно принять за начальную скорость без приведения к дульному срезу, так как расстояние до щита было всего 10 м. За неподвижным щитом при проведении описанного опыта в классе устанавливается ящик с песком для перехвата пуль. Величина начальной скорости снаряда зависит от многих условий, основными из которых являются следующие. Вес снаряда. С увеличением веса снаряда при одном в том же заряде величина начальной скорости уменьшается (и наоборот). Такая зависимость начальной скорости от веса снаряда легко объясняется физически: одинаковая сила давления газов в стволе оружия придает снаряду меньшей массы большее ускорение. Эта зависимость и используется в подкалиберных артиллерийских снарядах: увеличение начальной скорости достигается за счет снижения общего веса такого снаряда. Вес заряда. С увеличением веса заряда при одном и том же весе снаряда начальная скорость увеличивается. В минометах и гаубицах, например, начальная скорость изменяется при помощи переменных зарядов. Для десятиперых мин 82-мм миномета начальная скорость зависит от веса заряда следующим образом (см. таб. 3). Переменные заряды широко используются в артиллерийских системах, позволяя придавать снарядам наиболее целесообразные начальные скорости для стрельбы на различные дальности по различным целям. 50 Таблица № 3. Зависимость начальной скорости от веса заряда. Наименование заряда Основной Первый (осн.+1 доп.) Второй (осн.+2 доп.) Третий (осн.+3 доп.) Вес заряда в (г) Около 8 Около 21 Около 34 Около 47 Начальная скорость (м /с) 70 132 175 211 Наибольшая горизонтальная дальность (м) 476 1505 2355 3040 При конструкторской отработке боеприпасов, при проведении пробных стрельб часто используют переменные заряды для проверки прочности гильз, изменения дальности стрельбы, придания различных начальных скоростей. Длина канала ствола. С увеличением длинны канала ствола до определенных пределов начальная скорость увеличивается, так как снаряд большее время подвергается действию давления газов. Стрельба, например, из автоматического пистолета Стечкина и пистолета Макарова ведется одним и тем же патроном. Длина нарезной части ствола пистолета Стечкина - 126 мм, а пистолета Макарова - 80 мм. Поэтому для первого V0 =340 м/с, а для второго V0 =315 м/с. Длина нарезной части ствола АК74 – 372 мм, а пулемета РПК74 – 549 мм. Поэтому для АК74 V0 =900 м/с, а для РПК74 – 960 м/с. Но увеличение длины ствола целесообразно только до тех пор, пока давление газов на дно снаряда превышает сопротивление движению снаряда в канале ствола (см. рис. 15). 1 F Рис. 15. Кривая давления на стенки канала ствола. F – сила сопротивления ствола; 1 – точка равноденствия сил сопротивления ствола и давления пороховых газов. Относительная длина ствола является одним из признаков деления орудий на пушки, гаубицы и мортиры. 51 Оружие, предназначенное для стрельбы с большими начальными скоростями (противотанковые и зенитные пушки, дальнобойные орудия), имеет большую длину ствола - 50 и более калибров. Начальные скорости этих снарядов достигают 800 м/си более. Орудия, предназначенные для стрельбы крутыми траекториями (гаубицы), имеют более короткие стволы - до 40 калибров. Минометы, автоматические и подствольные гранатомѐты, предназначенные для стрельбы снарядом на небольшие расстояния, имеют стволы длиной до 20 калибров и дают начальные скорости менее 300 м/с. Помимо перечисленных причин на величину начальной скорости влияет плотность заряжания и скорость горения пороха, которые соответствующим образом подбираются при конструировании данного образца оружия. Для боеприпасов с отсечкой пороховых газов начальная скорость зависит от длины штоков, участвующих в разгоне снаряда, и от схемы метания, которая используется для этих боеприпасов. Например, в схемах обратного метания начальная скорость зависит от массы штоков, участвующих в разгоне. В выстреле, состоящем из 3 штоков, разгон происходит ступенями (см. рис.16). 1 2 3 V 0 Рис. 16 Схема обратного метания. 1, 2, 3 – штоки. На графике V (l) (см. рис. 17) хорошо прослеживается резкое понижение скорости вследствие зацепления штоков за основную движущуюся массу в конце каждой стадии. Наблюдаем, что прирост скорости на третьей стадии небольшой по сравнению с приростом на второй стадии. Отсюда следует, что нерационально использовать большее количество штоков в данной системе. Продолжение графика V (l) (см. рис.17), обозначенное серой линией, показывает скорость, которую имел бы выстрел, если бы не было уменьшения диаметров штоков, а выдвигался бы один длинный шток длинной равной сумме длин выдвижения всех штоков. 52 Рис. 17. Графики зависимостей: t (l), V (l). График t (l) (см. рис.17) показывает, сколько времени затрачено для полного раскрытия штоков в данной схеме. Как уже отмечалось ранее, начальная скорость может быть увеличена следующими способами: уменьшением веса снаряда при том же заряде; увеличением плотности заряжания; увеличением объема зарядной каморы, а следовательно, и веса заряда (для сохранения плотности заряжания); увеличением максимального давления; увеличением длины канала ствола; увеличением силы пороха и приданием ему наиболее выгодной прогрессивности горения. 53 3.6. Кинетическая энергия снаряда Убойная и пробивная способность снаряда характеризуется его кинетической энергией (энергией движения), называемой также живой силой, которая сообщается снаряду пороховыми газами в момент вылета из канала ствола. Кинетическая энергия движущегося тела вычисляется по известной из физики 2 формуле: Ec qVc . 2g Кинетическая энергия снаряда является важной характеристикой, показателем его пробивной способности. Установлено, например, что пуля стрелкового оружия обладает достаточной убойной силой для вывода из строя человека, если ее кинетическая энергия не менее 8 кгм. Для поражения же самолета, имеющего легкие броневые покрытия, пуля крупнокалиберного пулемета должна иметь энергию около 100— 120 кгм. Результат ударного действия снаряда (пули) зависит от его энергии при встрече преградой. От чего зависит величина кинетической энергии снаряда? Пример. Определить начальную энергию пули Б-32, если ее вес 64 г и начальная скорость 945 м/с. Решение. Выразим вес пули в килограммах q=0,064 кг и, подставив данные в формулу, получим: Ес= 0,0648 * 945 2 2 * 9,81 57153,6 19,62 2913,03кгм. Как видим, 14,5-мм пуля обладает очень большим запасом работы и поэтому обладает высокой пробивной способностью. С потерей скорости снаряд резко теряет запас энергии, так как кинетическая энергия пропорциональна квадрату скорости снаряда. Для определения энергии снаряда у цели надо в приведенную формулу подставить скорость снаряда у цели. Определим, какой кинетической энергией будет обладать пуля Б-32 у цели, если скорость пули в этот момент будет 100 м/с. Ec 0,064 100 2 2 9,81 10000 0,064 19,62 32,62кгм . Полученный ответ можно было предугадать: скорость пули у цели в 10 раз меньше начальной, следовательно, энергия пули у цели меньше начальной в 100 раз. В таблицах стрельбы из стрелкового оружия даются величины энергии пули у цели на различные дальности стрельбы. Например, при стрельбе из ручного пулемета РПК на дальность 500 м кинетическая энергия пули у цели Ес=38 кгм на дальность 700 м Ес=20 кгм и т. д.[11] . Анализ данных из таблиц стрельбы показывает, что пули стрелкового оружия обладают достаточной убойной силой на дальности стрельбы до 1000 м пулей обр. 1943 г. и на дальности до 3000 м пулями обр. 1908 г., и до 1350 м пулей обр. 1974 г. [1, 4, 11]. 54 Хорошие баллистические качества пуль обеспечивают и достаточную пробивную способность. Так, 9-мм пистолетная пуля при стрельбе из пистолета Стечкина пробивает сосновую доску толщиной 2,5 см на расстоянии до 350 м; 7,62-мм пуля обр. 1943 г. пробивает армейскую каску на расстоянии 650 м (80—90% пробитий); 14,5-мм пуля пробивает 20-мм броню на расстоянии до 800 м (при угле встречи около 90°) [5, 8, 10]. Особое значение величина кинетической энергии имеет для боеприпасов при стрельбе по бронецелям. Большой запас кинетической энергии бронебойных снарядов обеспечивает высокую бронепробиваемость. Например, пуля ПС для АК74 на дальности 700 метров обладает кинетической энергией, равной 20 кгм, и пробивает стальной шлем (каску)[11]. 3.7 Явление отдачи Рассматривая явление выстрела как движение системы пороховые газы – снаряд - оружие, мы должны выяснить сущность явления отдачи оружия. Пороховые газы, образующиеся во время выстрела, давят во все стороны с одинаковой силой*. Давление на дно снаряда и на дно гильзы приводит к поступательному движению снаряда и ствола. Движение ствола и связанных с ним деталей в сторону, противоположную движению снаряда во время выстрела под действием давления пороховых газов, называется отдачей. Скорость отдачи. Из механики известно, что если на два тела, находящихся в покое, действует одинаковая по величине сила, то скорость движения этих тел обратно пропорциональна их массам (весам): Q:q=V0 : Vотд., где: Q - вес оружия; Vотд. - скорость отдачи. Отсюда скорость отдачи равна: Vотд. q V0 . Q Но эта формула не учитывает влияния на скорость отдачи последействия газов и поэтому не дает величины наибольшей (максимальной) скорости отдачи. Формула наибольшей скорости отдачи может быть решена следующим образом. Составим уравнение количеств движения при выстреле. Количеством движения называется произведение массы тела на его скорость. Сумма количеств движения системы, вызываемых действием лишь внутренних сил, равна нулю: -М·Vm+m1·V0+m2u = О, *В действительности давление на дно снаряда и дно гильзы различно: давление на дно гильзы несколько больше, чем на дно снаряда. Однако для наших расчетов этой разницей можно пренебречь. 55 где -М·Vm — количество движения оружия назад (взято со знаком минус); m1·V0 - количество движения снаряда; m2·u - количество движения порохового заряда; u - средняя скорость истечения газов. Найдем из составленного уравнения наибольшую (максимальную) скорость отдачи, которая обозначается Vm , заменив предварительно массы через вес, так как веса пропорциональны массам: -Q·Vm+(q+0,5ω)·V0+ω·u=0; Q·Vm=q·V0+ω·u; Vm q V0 u Q , где ω – вес заряда. В числителе правой части вынесем V0 за скобку: (q Vm u )V0 V0 . Q Среднюю скорость истечения газов из канала ствола u для стрелкового оружия обычно принимают равной 1275 м/с. Отношение u/V0 называется коэффициентом последействия газов и обозначается через β. Тогда для стрелкового оружия β= 1275/V0. Этот коэффициент в среднем равен 1,6. Для начальных скоростей боеприпасов более 700 м/с значение коэффициента последействия газов точнее следует определять по формуле: β=0,15+1400:V0. С учетом коэффициента β формула выражает наибольшую скорость отдачи оружия и имеет вид: Vm (q )V0 Q . Эту формулу сравним с формулой, выражающей скорость отдачи без учета веса заряда и истечения газов: Vотд. qV0 . Q Они отличаются лишь тем, что в полной формуле вместо сомножителя q имеют скобку (q + βω), причем (q + βω) всегда больше q. Значит, скорость отдачи при решении задач по полной формуле будет всегда больше, чем скорость, найденная по приближенной формуле. Найдем скорость отдачи ствола 30-мм автоматической пушки 2А42, если еѐ вес 115 кг, вес снаряда 0,4 кг, вес заряда 0,128 кг и начальная скорость снаряда 990 м/с. Vm (q )V0 Q ; Vm (0,4 56 0,128) 990 ; 115 β=0,15+(1400:990) ≈1,4; Vm=(0,4+1,4x0,128)990:115) ≈4,97 м/с. Это скорость свободного не торможенного отката. В действительности же, при действии противооткатных устройств орудия скорость отката в момент вылета снаряда составляет 2,4 - 2,7 м/с. Решим пример для стрелкового оружия. Определить наибольшую скорость отдачи 7,62-мм снайперской винтовки при стрельбе пулей обр. 1908 г., если вес пули q=0,0096 кг; вес заряда ω=0,0031 кг; начальная скорость V0 =830 м/с, вес винтовки (заряженной) Q=4,4 кг. Определим коэффициент последействия: β=1275:830≈1,5. Подставим данные в формулу: Vm 0,0096 1,5 0,0031 830 4,4 2,6 м / с. Такая скорость отдачи (2 - 3 м/с) воспринимается стрелком совершенно безболезненно. Подсчитаем теперь скорость отдачи винтовки без учета последействия газов: Vотд.=(0,0096·830):4,4=1,81 м/с. По сравнению с действительной наибольшей скоростью отдачи (2,85 м/с) результат решения на 31% меньше. Следовательно, для верной характеристики явления отдачи надо рассчитать скорость отдачи с учетом последействия газов. Существует ещѐ одна формула для определения скорости отдачи с учетом веса заряда, но без учета истечения газов в период последействия. Напишем вновь уравнение количеств движения системы при выстреле и заменим массы через веса: -Q·Vm +q·V0 +ω·u1=0‚ где u1 — средняя скорость движения газов порохового заряда внутри канала ствола. Так как скорость движения газов порохового заряда изменяется от нуля в начале явления выстрела до V0 к моменту вылета пули (считают, что газы к моменту вылета обладают такой же скоростью, какой обладает пуля), то средняя скорость движения газов может быть принята как среднее арифметическое: u1=(0+V0):2=V0:2. Подставим полученное выражение в общее уравнение количеств движения системы и найдем из него Vm=(q·V0+ω(V0:2)):Q. Вынесем V0 за скобку и получим: Vm=(q+ω:2)·V0):Q. Эта формула показывает скорость отдачи без учета реакции истечения газов в период последействия и в таком виде приведена в книге Н.М. Филатова «Краткие сведения об основаниях стрельбы из винтовок и пулеметов». 57 Энергия отдачи. Вес оружия обозначается через Q, через Vm максимальную скорость отдачи, найденную выше. Тогда для определения энергии (живой силы) отдачи общая формула, выражающая величину кинетической энергии, примет такой вид: Em Зная, что Vm (q ) V0 Q Q Vm2 . 2g , подставим значение Vm в формулу Еm. Em Q (q ) 2 V02 . 2g Q 2 Сократим числитель и знаменатель на Q и получим: Em (q ) 2 V02 . 2g Q Анализируя формулу, легко установить, что энергия отдачи прямо пропорциональна весу снаряда и заряда, и квадрату начальной скорости снаряда, но обратно пропорциональна весу оружия. Определим наибольшую энергию отдачи в условиях предыдущего примера, где нами была рассчитана наибольшая скорость отдачи винтовки в 2,6 м/с: Em Q Vm2 (вес винтовки =4,4 кг); 2g Em=(4,4·2,62):(2·9,81)=1,5кгм. Следует заметить, что по выведенным формулам энергия отдачи определяется только для неавтоматического оружия. Приведенные зависимости дают приблизительные значения для определения энергии отдачи и для автоматического оружия, действующего по принципу отвода части газов. Определение энергии отдачи для автоматического оружия, действующего по принципу использования энергии отдачи, более сложно, так как необходимо учитывать целый ряд дополнительных факторов. В этих образцах оружия часть энергии отдачи используется полезно, а в неавтоматическом оружии отдача оказывает вредное действие. Способы уменьшения отдачи. При стрельбе из автоматов, винтовок, ручных пулеметов отдача воспринимается плечом стрелка. Поэтому должно быть вполне понятным стремление по возможности уменьшить энергию отдачи и установить для каждого вида оружия пределы, выше которых энергия отдачи не должна быть. Из приведенной выше формулы видно, что уменьшить энергию отдачи можно следующими путями: - уменьшить начальную скорость снаряда, но это нецелесообразно, так как требуемая начальная скорость задается при проектировании оружия, уменьшение же ее может привести к ухудшению баллистики снаряда; 58 - уменьшить вес заряда за счет применения порохов, обладающих большей силой, но так, чтобы это не приводило к уменьшению начальной скорости; - увеличить вес оружия, но это также нежелательно, ибо ухудшает маневренные свойства оружия. Следовательно, при проектировании оружия необходимо учесть все условия и выбрать такую комбинацию величин, чтобы, не ухудшая свойств оружия, иметь по возможности наименьшую энергию отдачи. Установлено, что для ручного оружия энергия отдачи не должна превышать 2 кгм. Рассмотренное явление отдачи, в целом вредно сказывающееся при стрельбе из стрелкового оружия, используется в некоторых видах автоматического оружия для приведения в действие подвижных частей. К этим образцам относится оружие, автоматика которых работает по принципу использования энергии отдачи. Из современных образцов Российского стрелкового оружия к этому классу относятся пистолеты ТТ, Макарова, Глок и т.д. [15]. У некоторых видов огнестрельного оружия применяются для уменьшения отдачи особые приспособления — дульные тормоза [15]. Дульный тормоз представляет собой специальное приспособление на дульной части ствола, действуя на которое, пороховые газы после вылета снаряда уменьшают скорость отдачи оружия. Идея использования дульного тормоза, как поглотителя энергии отдачи, зародилась еще в середине ХIХ в. В русской артиллерии дульный тормоз впервые был применен в 1862 году для трехпудовой бомбовой пушки обр. 1838 г. Устройство его было простое: в стенке ствола вблизи дульного среза было восемь окон, наклоненных к оси ствола под углом 45˚. В конце ХIХ века был использован более эффективный дульный тормоз, предложенный русским артиллеристом, профессором Артиллерийской академии Дурляховым. Эти тормозы были применены для орудий с жестким лафетом. Создание в начале ХХ века противооткатных устройств позволило избежать применения дульных тормозов. В настоящее время, в связи с повышением могущества орудий, для сохранения их максимальной подвижности дульные тормозы вновь получили широкое распространение. Принцип действия дульного тормоза легко объясняется на примере устройства ствола пулемета ДШК (рис.18а). Истекающие вслед за пулей пороховые газы ударяются в стенки дульного тормоза, уменьшая этим действие отдачи. Такой тип тормоза называется активным. Кроме этого, существуют тормозы реактивного и комбинированного типа. Их действие понятно из рис. 18б, в. 59 Рис. 18. Типы дульных тормозов В заключение можно указать, что современные конструкции дульных тормозов для артиллерийских систем поглощают до 30% и выше энергии отдачи. Для орудий малого калибра и стреляющих с большой начальной скоростью коэффициент действия дульных тормозов может доходить до 50 70% и выше. 3.8. Образование угла вылета. Меры соблюдения его однообразия Рассмотрим явление, происходящее при выстреле, движения снаряда и движения оружия под действием пороховых газов. Однако, помимо этого вопроса, практический интерес представляет еще одно явление, связанное с выстрелом. Помимо движения оружия (ствола) назад, отдача приводит также и к отклонению ствола от первоначального положения в вертикальной плоскости. Это происходит по следующим причинам. Сила действия пороховых газов Р направлена вдоль канала ствола по направлению движения оружия. Точка приложения этой силы расположена выше центра тяжести оружия, поэтому помимо движения назад ствол оружия еще поворачивается кверху. Такое положение будет в том случае, если оружие будет иметь точку крепления ниже центра тяжести. В условиях стрельбы из стрелкового оружия 60 стрелок, упирая приклад в плечо, этим противодействует силе Р, а так как расстояние между осью канала ствола и линией приложения силы противодействия Р несколько больше, чем расстояние от оси канала ствола до центра тяжести, то и вращательный момент в этом случае несколько увеличивается. Таким образом, во время выстрела оружие может вращаться дульной частью кверху и в момент вылета пули направление оси канала ствола не совпадает с первоначальным. Образуется некоторый угол, называемый углом вылета [10]. Углом вылета (γ) называется угол, образованный направлением оси канала ствола наведѐнного оружия до выстрела и направлением той же оси в момент вылета снаряда из канала ствола [10]. Кроме указанной причины, на образование угла вылета оказывает влияние вибрация ствола. Ствол представляет собой как бы упругий стержень, закрепленный на одном конце. При движении снаряда ствол совершает колебательные движения – вибрирует. Пуля получает при вылете направление в зависимости от положения дульной части ствола. Сочетание влияния вибрации и поворота оружия вследствие отдачи может, привести и к отрицательному углу вылета, то есть направление вылета пули будет ниже направления оси канала ствола наведенного оружия. У некоторых образцов автоматического оружия, автоматика работает на принципе использования энергии части газов, отводимых через поперечное отверстие в канале ствола. Газы, пройдя газовую камору, ударяют о газовый поршень и отводят затворную раму назад. Реактивная сила газов действует в противоположном направлении на переднюю стенку газовой каморы. Когда газовое отверстие расположено сверху, то активно-реактивная сила действия газов имеет большую скорость и высокое давление, изгибают ствол дульной частью книзу, ствол делает «клевок» вниз (рис.19). Рис. 19. Образование угла вылета. При стрельбе из автоматического оружия при помощи специальных устройств - компенсаторов можно стабилизировать положение ствола при автоматической стрельбе. Компенсатор применяется в пистолетах-пулеметах, автоматах и является продолжением кожуха или ствола (пистолет-пулемет обр. 1941 г.). Передняя стенка компенсатора наклонная, в верхней стенке вырезано окно. Истекающие из ствола газы ударяют в переднюю стенку (рис. 20), чем несколько уменьшают отдачу (по принципу активного дульного тормоза) и, отражаясь от неѐ, истекают в окно верхней стенки, что приводит к опусканию 61 ствола после выстрела. Таким образом, компенсатор приближает ствол к первоначальному положению для последующего выстрела, повышая тем самым кучность стрельбы. Рис. 20. Компенсатор. Углы вылета определяются на специальных стрельбах, и в таблицах даются их средние значения. Так, например, среднее значение углов вылета для автомата АК74 минус 4 минуты, ручного пулемета РПК74 минус 2 минуты, для ПКМ, ПКМС, ПКМБ минус 12 минут, для автомата АКМ минус 6 минут, для КПВТ пуля Б-32 - ноль, для 76-мм танковой пушки минус 13 минут (для осколочно-фугасной гранаты ОФ-350), для 122-мм гаубицы обр. 1938 г. от нуля до плюс 3 минут (на различных зарядах) [9, 25, 31, 36]. Углы вылета учитываются при расчетах в таблицах стрельб и введением поправок. Однако при стрельбе из стрелкового оружия правильность изготовки существенно сказывается на разнообразие углов вылета пули. Стрелок при хорошей подготовке, точной и правильной прикладке может добиться однообразных по величине углов вылета и тем самым ликвидировать их вредное воздействие на качество стрельбы. Большое значение имеет учет индивидуальных углов вылета при стрельбе прямой наводкой из артиллерийских орудий, особенно из гаубиц, которые имеют плохую устойчивость при малых углах возвышения. Так, например, поправка дальности на угол вылета для 122-мм гаубиц обр. 1938 г. в среднем достигает 200 - 250м. Поэтому для каждых конкретных условий стрельбы прямой наводкой рекомендуется, по возможности, учитывать эти поправки. 3.9. Особенности выстрела из миномета В сравнении с выстрелом из нарезного оружия выстрелы из минометов отличаются некоторыми особенностями. Во-первых, горение боевого заряда сначала происходит в хвостовом патроне, где плотность заряжания равна 0,5-0,6; затем пороховые газы пробивают картонную гильзу и через отверстия в трубке стабилизатора вытекают в замкнутый объем, где воспламеняют дополнительные заряды. Плотность заряжания в заминном объеме оказывается равной 0,01. Во-вторых, в связи с тем, что заминный объем очень велик, а также велика поверхность стабилизатора и донной части мины, а скорость движения ми62 Рис. 21. График изменения давления газов и скорости мины в стволе 82-мм БМ. ны в канале ствола небольшая, значительная часть тепловой энергии уходит на нагревание стенок ствола и мины. Движение мины происходит вследствие суммарного давления газов основного и дополнительного зарядов. В-третьих, вследствие наличия зазора между миной и стенками ствола значительная часть газов (10 - 15%) прорывается в этот зазор и не участвует в придании мине скорости, в то время как в нарезном оружии доля газов, прорывающаяся по зазорам между ведущим пояском и нарезами ничтожна. Учитывая эти особенности, явление выстрела из миномета разделяют на следующие периоды: 63 - Давление форсирования – от момента воспламенения порохового заряда до момента прорыва пороховых газов через стенки порохового стакана в отверстия мины. - Первый период - от момента воспламенения дополнительных зарядов и начала движения мины до полного сгорания всего порохового заряда. В минометах максимальное давление наступает в конце горения порохового заряда. При стрельбе на наибольшем заряде из 82-мм миномета Рm=390-400 кг/см2 и наступает при прохождении мины 7 см пути. - Второй период - движение мины под действием расширяющегося постоянного количества газов, период от полного сгорания порохового заряда до момента вылета мины из канала ствола. Для наибольшего заряда 82-мм миномета Рд около 50 кг/см2; Vд = 200-210 м/с. Характер изменения давления газов и скорости мины в канале ствола 82мм миномета на основном и третьем заряде, показан на рис. 21. . 3.10. Особенности выстрела из реактивного оружия Прежде чем указать особенности выстрела из реактивного оружия, напомним основные понятия о действии реактивной силы. Сущность образования реактивной силы (R) можно объяснить следующим образом. С некоторыми упрощениями считают, что реактивная сила складывается из двух сил: Rcm - статической составляющей; Rд - динамической составляющей. Статическая составляющая Rcm возникает потому, что давление в переднюю стенку не уравновешено давлением на дно, так как в дне сосуда имеется отверстие (сопло). Rcm ( P Pa ) S , где: Р - давление газов в каморе сгорания; Ра - внешнее давление (атмосферное); S - площадь сопла. Динамическая составляющая (Рд) возникает потому, что скорость пороховых газов возрастает от нуля до скорости истечения u. При этом сопло, сообщающее газам ускорение, должно само получить ускорение в противоположную сторону. Величина силы определяется по закону Ньютона: Rcm ma , где m - масса газов, истекающая за время t; а - ускорение газовой массы за то же время. u u0 , но в нашем случае начальная скорость истечения t u u =0, следовательно, a . t Известно, что a 64 Тогда Rд mu m , но - есть масса газов, истекающая за 1 секунду mс. t t где mс. - масса вытекающих в секунду газов; Qс. - вес этих газов (секундный расход); u - скорость истечения газов. Из формулы Rcm ( P Pa ) S следует, что чем меньше будет давление среды Ра, тем больше будет Rcm. Следовательно, реактивная сила R будет больше всего при полете снаряда в безвоздушном пространстве. В тоже время: Rд mс u или Rд Qс u . g Из формулы Rд=mс.·u ясно, что Rд будет тем больше, чем больше скорость истечения u; следовательно, при полете в безвоздушном пространстве возрастает и Rд. Данная формула позволяет также понять значение расширяющего сопла, увеличивающего скорость истечения газов, а следовательно, и силу R.Сопло имеет обычно форму (рис. 22): сначала сужается, а затем расширяется. В сужающейся части сопла можно получить наибольшую скорость истечения газов. Это — критическая скорость, равная местной скорости звука. Для пороховых газов эта скорость достигает более 1000 м/с. В 80-х гг. XIX столетия было установлено, что газ, получив в сужающейся трубе критическую скорость, попадая далее в расширяющуюся насадку, двигается по ней со сверхзвуковой скоростью. Таким образом, при дозвуковых скоростях уменьшение сечения трубы увеличивает скорость потока, а при сверхзвуковых скоростях* увеличение скорости истечения происходит при расширяющемся сопле. Сужающуюся (входную) часть сопла делают более крутой, чтобы Рис. 22. Форма сопла. * В обоих случаях имеется в виду местная скорость звука. 65 уменьшить его длину. Расширяющуюся же часть сопла делают более длинной с тем, чтобы не допустить отрыва потока от стенок. Диаметр выходного сечения обычно в 2 - 3 раза больше диаметра критического сечения. Из рассмотренных положений можно сделать вывод об особенностях выстрела из реактивного оружия (СПГ-9, РПГ-7В): - предварительный период: сопло закрыто поддоном, который рассчитан так, что разрушается с началом движения снаряда при давлении р0; - порох горит в полузамкнутом пространстве, давление и скорость истечения газов растут, пока не установится равновесие; - скорость снаряда возрастает на некотором участке траектории после вылета снаряда из ствола (схода с направляющих). Наибольшая скорость реактивного снаряда называется начальной скоростью. Она примерно в 1,5 раза больше дульной скорости (скорости схода); - отдача оружия при выстреле уравновешивается реактивной силой вытекающих из сопла пороховых газов. Было разработано три типа безоткатных орудий: орудие типа открытой цилиндрической трубы; безоткатное орудие с осевым отводом газов; безоткатное орудие с перфорированной гильзой. В настоящее время широкое распространение получили безоткатные орудия с осевым отводом газов, в которых сила отдачи при выстреле уравновешивается реактивной силой вытекающих пороховых газов (РПГ-7В, СПГ-9). При выстреле часть пороховых газов выходит через казенную часть орудия (через сопловые отверстия затвора) в направлении, обратном движению снаряда. При этом возникает реактивная сила, направленная вперед, которая и уравновешивает силу отдачи. Такие орудия получили название безоткатных. Величина реактивной силы, а следовательно, и «безоткатность орудия»зависит от площади критического сечения сопловых отверстий. Эти отверстия подбираются так, чтобы реактивная сила была равна силе отдачи, чем достигается «безоткатность орудия». В результате отпадает необходимость в противооткатных устройствах или опорных плитах и резко уменьшается вес станка (лафета). Ствол безоткатного орудия по сравнению с обычными артиллерийскими орудиями также существенно облегчен за счет уменьшения толщины стенок, так как максимальное давление газов в каморе сгорания не превышает 700-800 кг/см2. В целом, например, вес батальонного безоткатного орудия 82-мм калибра составляет 86 кг. Кроме того, важными достоинствами современных безоткатных орудий являются простота их конструкции. Основные недостатки: демаскирующее действие пороховых газов; наличие опасной зоны позади сопла (до 30-40 метров) вследствие истечения пороховых газов назад; трудность получения начальных скоростей снаряда свыше 400-450 м/с из-за низкого коэффициента использования порохового заряда и неудобства обслуживания. 66 Наличие перечисленных достоинств и недостатков обуславливает характер использования безоткатных орудий. Они применяются для вооружения мотострелковых, горнострелковых и воздушно-десантных подразделений и подразделений специального назначения, где малый вес системы в сочетании с могуществом боеприпаса является решающим. 67 Глава IV. Сведения из внешней баллистики 4.1. Предмет и задачи внешней баллистики. Траектория снаряда и ее элементы Внешней баллистикой называется наука, изучающая движение снаряда после прекращения действия на него пороховых газов [10]. Данное определение можно считать правильным, но в науке произошли изменения, и в настоящий момент более верным будет признать такое определение: «Внешней баллистикой называется наука, изучающая движение снаряда в поле гравитации и воздушной среде». Вылетев из канала ствола под действием пороховых газов, снаряд двигается в воздухе по инерции. Линия, описываемая центром тяжести движения снаряда при его полѐте, называется траекторией [8, 10]. Для того чтобы решать практические задачи, связанные со стрельбой, необходимо знать свойства траектории данного вида оружия и еѐ форму; время, за которое снаряд пролетает то или иное расстояние; общую дальность полета снаряда; и полѐта снаряда с тангажем над линией прицеливания и много других вопросов. Основной задачей внешней баллистики является решение вопроса о том, с какой начальной скоростью, под каким углом возвышения нужно бросить снаряд определенной формы, чтобы он достиг данной точки на поверхности земли, водной поверхности или в пространстве. В настоящее время эта задача решена достаточно полно и на основе ее решения рассчитываются все таблицы стрельбы и шкалы прицельных приспособлений оружия. Кроме того, внешняя баллистика решает и ряд других задач, связанных со стрельбой. Важнейшими из них являются, учет влияния метеорологических условий на полет снаряда и составление поправочных таблиц - теория поправок, а также исследование полета вращающихся снарядов. В практической деятельности, связанной с применением оружия на поле боя, пользуются выводами внешней баллистики. Выбирая исходные установки угломера, прицела и уровня для стрельбы из орудий и минометов, из стрелкового оружия выбирая прицел и точку прицеливания, внося поправки в установку прицела и целика на ветер, температуру и другие условия стрельбы, определяя упреждение при стрельбе по движущимся целям, пользуются таблицами, которые дает внешняя баллистика. Организуя систему огня, определяя, где можно поразить противника огнем стрелкового оружия, где пушечной артиллерией, а где огнем гранатометов, гаубиц и минометов, пользуются знаниями свойств траекторий данных видов оружия. Данные знания дает внешняя баллистика. При всех действиях на поле боя связанных с построением боевого порядка, маневром подразделений и т.д., всегда учитывают огневые средства противника, избегая возможности одновременного поражения наших подразделений настильным и навесным огнем, учитывая наличие мертвых пространств и 68 возможность использования различных укрытий и т. п. Эти сведения также дает внешняя баллистика. Для изучения сил внешняя баллистика сначала рассматривает движение снаряда без учета силы сопротивления воздуха под действием только силы тяжести (параболическая теория). После этого рассматривается движение снаряда как вращающегося тела с учетом действия сил тяжести и сопротивления воздуха. Прежде чем приступить к изучению этих вопросов, ознакомимся с основными терминами и определениями, принятыми во внешней баллистике (рис. 23). - Точка вылета (0) - точка, в которой находится центр тяжести снаряда в момент вылета. Момент вылета – это момент прохождения дна снаряда через дульный срез ствола. Для упрощения рассуждений за точку вылета принимают центр дульного среза ствола. Д В Рис. 23. Элементы траектории. - Горизонт оружия (ОС) - горизонтальная плоскость, проходящая через точку вылета. - Линия бросания (ОВ) - продолжение оси канала ствола в момент вылета. - Линия выстрела (ОД) – направление оси канала ствола наведенного 69 оружия. В Наставлении по стрелковому делу «Основы стрельбы из стрелкового оружия» эту линию называют линией возвышения. - Вершина траектории (S) – наивысшая точка траектории. - Высота траектории (Н) – расстояние от вершины траектории до горизонта оружия. - Точка падения (табличная) (С) - точка пересечения траектории с горизонтом оружия. - Горизонтальная дальность (Х) – расстояние по горизонту оружия от точки вылет до точки падения. - Угол возвышения (Υ) - угол, заключенный между линией выстрела и горизонтом оружия. - Угол бросания (Θ0) - угол, заключенный между линией бросания и горизонтом оружия. - Угол вылета (α) - угол, заключенный между линией выстрела и линией бросания. Угол вылета может быть положительным, когда линия бросания проходит выше линии выстрела, и отрицательным, когда линия бросания проходит ниже линии выстрела. - Угол падения (табличный) (Θс) – угол, заключенный между касательной к траектории в точке падения и горизонтом оружия. - Плоскость стрельбы – вертикальная плоскость, проходящая через линию выстрела. - Плоскость бросания – вертикальная плоскость, проходящая через линию бросания. - Восходящая ветвь траектории (ОS) – расстояние от точки вылета до вершины траектории. - Нисходящая ветвь траектории (SC) – расстояние от вершины траектории до точки падения. - х, у - координаты, определяющие положение снаряда в пространстве. 4.2. Движение снаряда под действием силы тяжести Действие сил тяжести не зависит от скорости полета снаряда. Поэтому понижение снаряда во время полета под линией бросания также будет совершаться по закону свободного падения тел и снарядов, выпущенных под какимто углом к горизонту оружия, опишет кривую, показанную на рис.24. В конце первой секунды полета под действием силы тяжести снаряд будет не в точке «а1» или «а», а в точке А. Это происходит в результате поступательного движения снаряда в первоначальном направлении и движения его под действием силы тяжести. Рассматривая аналогичное положение снаряда в конце 2, 3 и т.д. секунд, мы получим точки Б, В и т.д. (рис. 24). Сокращая последовательно промежутки времени, через которые мы определяли положение снаряда, можно получить ряд очень близко отстоящих друг от друга точек. Соединив эти точки кривой, мы получим графическое изображение траектории полета снаряда без учета силы сопротивления воздуха. 70 Уравнение параболической траектории. Математическим выражением закона движения снаряда является уравнение траектории, которое отражает зависимость между координатами х и у в любой точке полета снаряда. Выведем уравнение траектории снаряда, летящего под действием только одной силы тяжести. Допустим, что в безвоздушном пространстве мы произвели выстрел из орудия под углом бросания Θ0 с начальной скоростью равной V0 (рис. 25). Вылетев из ствола, снаряд опишет какую-то траекторию и упадет в точке Д. Необходимо найти, на какой высоте над горизонтом оружия летит снаряд на удалении х от точки вылета при данных значениях V0 , Θ0. Для вывода уравнения поместим начало системы координат в точке вылета, как это показано на рис. 25. Из рисунка видно, что у=АВ-АС. Определим значения АВ и АС. Значение АВ находится из треугольника ОАВ АВ=х·tgΘ0. Рис. 24. Понижение снаряда под линией бросания АС есть не что иное, как понижение снаряда под линией бросания за время его полета до точки С. Понижение, как путь, проходимый свободно падающим телом, определяется по формуле: AC h gt 2 . 2 71 д Х1 Рис. 25. К выводу уравнения параболической траектории Время полета снаряда до точки С находится следующим образом: OA . V0 OA V0 t , откуда t x Cos Из треугольника ОАВ видно, что OA Таким образом: Тогда: t AC x V0 Cos . 0 . 0 gx 2 2V02 Cos 2 . 0 Подставив найденные значения АВ и АС в выражение у=АВ-АС, получим уравнение траектории: y x tg 0 gx 2 2V0 Cos 2 . 0 Полученное уравнение описывает траекторию снаряда, которая представляет параболу в безвоздушном пространстве под действием только одной силы тяжести. Траектория полета снарядов в безвоздушном пространстве представляет собой кривую, называемую параболой. Поэтому траекторию полета снарядов в пустоте называют параболической траекторией. Параболические траектории имеют следующие свойства: - траектория представляет собой плоскую симметричную кривую, относительно вершины, т.е. вершина траектории, находится посредине полной горизонтальной дальности; - восходящая ветвь траектории равна нисходящей ветви; 72 - время полета снаряда от точки вылета до вершины равно времени полета от вершины до точки падения; - угол падения по своей абсолютной величине равен углу бросания; - окончательная скорость снаряда равна его начальной скорости; - угол наибольшей горизонтальной дальности равен 45º. При стрельбе в воздухе снарядами с небольшими начальными скоростями их траектории близки к параболическим. Поэтому, как указывалось в очерке по истории баллистики, долгое время все расчеты для стрельбы велись по выведенному уравнению параболической траектории. Справедливость такого допущения можно показать на следу ющем опыте. У Θ Х Рис. 26. Схема опыта Зная начальную скорость снаряда учебной мортирки (около 12 м/с) (рис. 26), определим, пользуясь выведенным уравнением траектории, на какой высоте будет лететь «снаряд» в 5 метрах от точки вылета, если «выстрел» будет произведен под углом Θ=15º. После расчетов произведем выстрел по экрану и убедимся, что снаряд пробьет экран на рассчитанной высоте у. Для определения высоты полета снаряда найдем значение «у» по уравнению параболической траектории, если V0=12 м/с; х=5 м; 15 0 ; Cos15º=0,9659; tg15º=0,268. 0 y y y x tg 0 gx 2 2V02 Cos 2 ; 0 9,81 5 2 ; 2 12 2 Cos 2 15 0 9,81 25 5 0,268 1,3395 0,912 2 144 0,9659 2 5 tg15 0 0,43 м. Проделав данный расчет по контрольному квадранту от 82-мм миномета, придадим мортирке угол возвышения 15º и произведем несколько выстрелов по бумажному экрану-мишени с расстояния Х = 5 м. Высота пробоин (около 43 см) совпадает с расчетами до опыта. По уравнению параболической траектории можно примерно рассчитать превышение траектории мины при стрельбе из 82-мм батальонного миномета на основном заряде, при котором начальная скорость мины всего 70 м/с. 73 Расчет проводится для Θ0=45º, задаваясь различными значениями х по уравнению траектории. Для облегчения решения предварительно подсчитаем постоянное значение K 2V 2 0 g Cos 2 ; 0 Тогда получим: у = х - 0,002 х². Сведем полученные данные в таблицу и построим в масштабе траекторию полета мины (рис. 27). Таблица № 4. Х(м) У(м) 0 0 100 80 200 120 300 120 400 80 500 0 Определение элементов траектории. Определение полной горизонтальной дальности и горизонтальной дальности до вершины траектории. Для того чтобы определить, на какую дальность полетел бы снаряд в безвоздушном пространстве с данной начальной скоростью и данным углом бросания, необходимо решить уравнение траектории относительно «х». Рис. 27. Траектория полѐта 82-мм осколочной мины при стрельбе на основном заряде с прицелом 10-00 (45º). Так как полная горизонтальная дальность есть расстояние по горизонту оружия от точки вылета до точки падения, то превышение траектории «у» в точке падения будет равно нулю. Подставляя в уравнение траектории 74 y x tg 0 2V02 gx 2 Cos 2 2V02 gx 2 Cos 2 0 значение y=0, получим: 0 x tg 0 . 0 Вынесем «х» за скобки: х 0 tg 0 2 0 2V gx Cos 2 . 0 Произведение может быть равно нулю в том случае, если из сомножителей или «х», или выражение в скобке будет равно нулю. В первом случае получим х1=0, что соответствует точке вылета. Приравнивая выражение в скобках к нулю, получим: tg 0 2 0 2V gx Cos 2 2V gx Cos 2 gx 2V02 Cos 2 2 0 tg 0; 0 0 ; 0 0 tg 0 ; откуда: 2V02 Cos 2 0 tg 0 x . g Sin 0 , tg 0 Cos 0 2V 2 .Cos 0 .Sin 0 V02 Sin 2 0 x= 0 . g.Cos 0 g Но тогда Пример. Определить, на какую дальность полетит пуля, выпущенная под углом Θ0=15º с начальной скоростью V0=825 м/с (тяжелая пуля обр. 1908 г. при стрельбе из пулемета ПКМ) при отсутствии силы сопротивления воздуха. Решение: X 8252 Sin30 0 9,81 68550 м . При изучении этого вопроса с курсантами (офицерами) можно продемонстрировать справедливость выведенной формулы на опыте с учебной мортиркой. Определим дальность полета снаряда мортирки при угле бросания Θ0=15º. X V02 Sin 2 g 0 ; X 12 2 Sin(2 150 ) 9,81 7,5 м . Проверка стрельбой подтверждает, что полная горизонтальная дальность полета снаряда мортирки при V0=12 м/с и Θ0=15˚равна около 7,5 м. 75 Исходя из того, что траектория есть симметричная кривая, и вершина ее находится на половине полной горизонтальной дальности, можно написать для определения горизонтальной дальности до вершины: V02 Sin 2 2g 1 X 2 x 0 . Определение начальной скорости и угла бросания. Используя формулу X V02 Sin 2 2g 0 мы можем определить величину , начальной скорости или угол бросания, чтобы получить заданную величину полной горизонтальной дальности. Пример. Определить скорость, с которой была брошена ручная граната из окопа, если она пролетела 30 м, а бросок совершен под углом в 45° к горизонту. Решение: Преобразуем последнюю формулу для начальной скорости. X g V02 Sin 2 0 Xg Sin 2 ; V02 ; V0 0 Xg Sin 2 . 0 Подставляя данные из условия задачи, получим: 30 9,81 Sin90 0 V0 30 9,81 16 м с . Решим задачу на определение угла бросания. Пример: Под каким углом нужно стрелять из 82-мм батальонного миномета основным зарядом, чтобы мина полетела на дальность 200 м? Решение. Преобразуя формулу X получим: Sin 2 0 g X ; V02 V02 Sin 2 2g Sin 2 0 для выражения Sin2Θ0, 9,81 200 70 2 0 0,4 . По таблицам тригонометрических величин находим, что при значении Siп2Θ0=0,4 угол 2Θ0 . Следовательно, угол Θ0 должен быть равен 11˚ 47΄,что соответствует Θ=78º 13´. Сравнивая результаты с таблицами стрельбы, видим, что в расчете мы допустили ошибку, равную всего 42΄. Определение времени полета снаряда. Для определения времени полета снаряда необходимо использовать уже имеющуюся у нас при выводе уравнения траектории зависимость x V0 t Cos 0 . Из этого выражения следует: t x V0 Cos . 0 Полное время полѐта «Т» определяется, если в эту формулу подставим значение полной горизонтальной дальности «Х», тогда T X V0 Cos 76 . 0 Определение высоты траектории «У». Высоту траектории У можем определить, если подставим в уравнение траектории значение величины горизонтальной дальности до вершины траектории: V02 Sin 2 2g xs Тогда Y=xstg У 2 0 V У У Sin 2 0 tg 2g 2 0 V V02 Sin 2 g 0 2Sin 0 tg 2g 0 0- 2V02 0 0 . gx s2 2V02 .Cos 2 0 g Cos 2 V02 Sin 2 2g 0 ; 4 0 g V 4Sin 2 0 Cos 2 2V02 Cos 2 0 4 g 2 2 0 0 ; ; 1 V02 Sin 2 0 , откуда окончательно: 2 g V02 Sin 2 0 . У 2g Пример. Определить высоту траектории при стрельбе из 82-мм миномета на третьем заряде, если установка прицела 4-00 (Θ0=81˚). Решение: У 2112 Sin 2 810 2 9,81 2130 м. Проведенные расчеты, сделанные по формулам параболической теории, позволяют уяснить, как внешняя баллистика решает задачи по исследованию свойств траектории и определению еѐ элементов при V<70 м/с. 4.3. Движение снаряда в воздухе При движении снаряда в воздухе кроме силы тяжести на него действует сила сопротивления воздуха. Величина силы сопротивления воздуха, а следовательно, и интенсивность воздействия на снаряд, может значительно превосходить силу тяжести. Эта разница тем больше, чем меньше вес снаряда и больше скорость его полета. При этом необходимо отметить, что величина силы сопротивления возрастает особенно резко при движении снарядов со скоростями, превышающими скорость звука. Эти положения наглядно подтверждаются следующей таблицей № 5. Таблица № 5. Соотношение силы аэродинамического сопротивления к весу снаряда. R q d мм q кг Vм/ dvс V 500 700 7,62 0,011 23 42 77 76,2 6,5 4,5 8,2 152,4 50 2,2 4,1 Из таблицы видно, что сила сопротивления воздуха при полете 82-мм мины со скоростью 70 м/с составляет всего 0,08 от веса мины (силы тяжести). Сила сопротивления воздуха, действующая на винтовочную пулю, летящую со скоростью 825 м/с, в 40 - 80 раз больше силы тяжести от веса мины. О величине влияния силы сопротивления воздуха на полет снаряда со скоростью, превышающей скорость звука, можно судить по следующим примерам. Дальность полета пули в безвоздушном пространстве при угле бросания 15˚и начальной скорости 825 м/с, независимо от еѐ размеров и формы, была бы равна, как показывает ранее решенный пример, 68550 м. Дальность полета пули обр. 1908 г. при тех же условиях, но при наличии силы сопротивления воздуха равна лишь 3825 м, т.е. в 17 раз меньше, чем в безвоздушном пространстве. Сила сопротивления воздуха является одним из главных факторов, препятствующих достижению больших дальностей стрельб. Разнообразие форм современных пуль и снарядов во многом определяется необходимостью уменьшить величину силы сопротивления. Причины возникновения силы сопротивления воздуха. Сопротивление воздуха полету вызывается тремя основными причинами: вязкостью воздуха, отрывом пограничного слоя с образованием завихрения и образованием баллистической волны. Каждая из этих причин проявляется в результате давления воздуха на снаряд или возникновения сил трения. Вязкость воздуха, образование пограничного слоя. Вязкость воздуха объясняется наличием внутреннего сцепления между частицами воздуха. При движении снаряда происходит следующее явление. Частицы воздуха, непосредственно примыкающие к снаряду, вследствие сцепления с его поверхностью, движутся со скоростью снаряда. Следующий слой частиц воздуха в результате внутреннего сцепления также приходит в движение, но уже с несколько меньшей скоростью. Движение этого слоя передается следующему, и так до тех пор, пока разность скоростей частиц не станет равной нулю. Образуется так называемый пограничный слой (рис. 28). Рис. 28. Образование пограничного слоя. 78 Пограничный слой образуется как при движении снаряда со скоростью меньшей скорости звука, так и при движении со скоростью большей скорости звука. В пограничном слое возникают касательные напряжения, которые можно отнести к силам трения. На их преодоление расходуется часть энергии снаряда, что и приводит к уменьшению скорости его полета. Понятно, что тщательная обработка поверхности снаряда уменьшает сопротивление воздуха, на всех скоростях. Отрыв пограничного слоя и образование завихрений. Если слой воздуха, раздвинутый головной частью снаряда, снова сомкнется сразу за снарядом, то сопротивление воздуха будет наименьшим. Кинетическая энергия снаряда будет расходоваться только на раздвигание слоя воздуха и преодоление сил трения, возникающих в пограничном слое. Однако такого положения можно достигнуть только при наличии особой сигарообразной формы снаряда (рис. 29) и при крайне малых скоростях его полета. Реальные же скорости полета современных снарядов во много раз превосходят скорости формирования ламинарного потока. При движении снаряда с плоским дном, пограничный слой, достигнув донного среза, отрывается от него. За дном образуется разреженное пространство, куда засасываются частицы воздуха из пограничного слоя. Пограничный слой скатываясь, образует турбулентные завихрения (рис. 30). Рис. 29. Картина ламинарного обтекания воздухом тела сигарообразной формы. В связи с этим давление за донной частью ниже атмосферного, и снаряду приходится преодолевать эти разности давлений. Ратм. Р<Ратм. Рис. 30. Образование завихрений. При движении снарядов со скоростью меньшей скорости звука образование завихрения является главной причиной сопротивления воздуха. На характер завихрения особенно влияет форма хвостовой части. Конусообразная или каплевидная сходящаяся форма хвостовой части наиболее выгодна для снаря79 дов, имеющих скорость меньшую скорости звука. Форма головной части имеет гораздо меньшее значение. Образование баллистической волны. При движении снарядов со скоростями большими скорости звука появляется новый мощный фактор сопротивления воздуха - баллистические волны. Причины образования баллистической волны заключаются в следующем. При всяком колебании и движении тел в воздухе создаются бесконечно малые уплотнения, которые распространяются со скоростью звука. Если частота этих колебаний находится в пределах 20—20000 колебаний в секунду, мы воспринимаем их как звук. При движении снарядов со скоростью меньшей скорости звука эти уплотнения, распространяясь во все стороны, «обгоняют» снаряд и уходят вперед, не оказывая на него особенного влияния (рис. 31). Рис. 31. Схема распространения звуковых волн при движении снаряда со скоростью меньшей скорости звука. При скорости снаряда, равной скорости звука, эти уплотнения накладываются одно на другое у головной части, создавая уже более плотный слой (рис.32). 80 Рис. 32. Схема распространения уплотнений воздуха перед снарядом, летящим со скоростью звука. На рис. 33 помещена фотография полета пули со скоростью примерно равной скорости звука. На фотографии хорошо наблюдается фронт сгущения звуковых волн перед головной частью пули и за ее дном, а также видна волна сгущения у места обжимки пули. Еще более плотным оказывается слой воздуха, когда скорость снарядов становится большей скорости звука, и снаряд должен как бы «разрывать» уже образовавшуюся волну сгущения (рис. 34). Образуется баллистическая волна. Рис. 33. Фотография пули, летящей примерно со скоростью звука. Давление на фронте этой волны может достигать 8 - 10 атмосфер. Для преодоления такого большого давления у головной части расходуется наибольшая часть энергии снаряда, что приводит к резкому уменьшению скорости его полета. 81 Рис. 34. Схема образования баллистической волны. На рис. 35 показана фотография пули, летящей со скоростью большей скорости звука. Баллистическая волна (темная полоса) образуется не только у головной части, но и у хвоста и у некоторых других частей пули (неровности пули, след от обжимки и т. д.). Рис. 35. Фотография пули, летящей со сверхзвуковой скоростью. Таким образом, при движении снарядов со скоростями большими скорости звука главным фактором сопротивления является баллистическая волна — образование большого давления у головной части. Поэтому особое значение приобретает форма головной части снарядов. Головная часть снаряда не должна иметь площадок, выступов и должна быть по возможности заостренной. Впервые обратил внимание на важность заострения головной части пули Г.В.Киснемский, который в 1895 году предложил заостренную пулю. Наиболее выгодными в отношении уменьшения сил сопротивления воздуха являются снаряды, имеющие очертание головной части по так называемой кривой наименьшего сопротивления, впервые рассчитанной русским ученым — артиллеристом С.Петровичем. Очертание головной части современных снарядов и пуль приближается к этой кривой. Таблица № 6. Соотношение сопротивлений при различных скоростях. Скорость V<a V>a трения 20…30 15…20 Сопротивление % донное 80…70 35…40 волновое 50…40 Сила сопротивления воздуха. Суммарная сила сопротивления, образующаяся вследствие вышеуказанных причин, и есть полная аэродинамическая сила. 82 Точка приложения силы сопротивления называется центром сопротивления (рис. 36). Рис. 36. Расположение центра тяжести и центра сопротивления у неоперенного снаряда и у мины. Вследствие значительной сложности такого явления, как сопротивление воздуха, до сих пор нет полной теоретической зависимости, выражающей величину силы сопротивления. Существует ряд эмпирических формул для выражения силы сопротивления воздуха R. Приведем одну из них: R C V2 S, 2 где С – баллистический коэффициент, S – площадь поперечного сечения снаряда. Сила сопротивления воздуха зависит от следующих причин: Формы снаряда. В формуле эта зависимость выражается через коэффициент формы «i». Коэффициент формы определяется из сравнения формы данного снаряда с формой снаряда, принятого за эталон с i=1 для определенного закона сопротивления, путем специальных стрельб. Чем меньше коэффициент формы «i», тем меньше сила сопротивления воздуха. По данным специальных стрельб, коэффициенты форм имеют следующие средние значения. Таблица № 7. Коэффициенты формы снарядов. Наименование снарядов Величина коэффициента формы 14,5 -мм пуля Б-32 7 7,62мм пуля обр. 1943 года 82-мм мина 7,62мм пуля обр. 1908 года мм 9-мм пистолетная пуля 0,46 0,56 0,59 0,61 0,98 Для сверхзвуковых скоростей, когда в сопротивлении воздуха основную роль играет образование баллистической волны, наиболее выгодным является снаряд с остроконечной головной частью длиной до 3,5 калибров и донной частью с небольшой конусностью для уменьшения завихрения. Такова форма тяжелой пули и всех дальнобойных снарядов. Калибр снаряда (d) - площадь поперечного сечения снаряда. 83 S d2 . 4 Сила сопротивления воздуха изменяется прямо пропорционально квадрату калибра. Это значит, что если калибр снаряда увеличить в 2 раза, то сила сопротивления воздуха увеличится в 4 раза. В развернутом виде зависимость для оценки силы R может быть представлена в виде: R 1000 id 2 H ( y) F (v) , g где i - коэффициент формы снаряда; d - калибр снаряда; H(у) - функция, показывающая изменение плотности воздуха с высотой; F(v) – функция, показывающая зависимость изменение плотности воздуха от скорости движения. Плотность воздуха. Влияние плотности воздуха учитывается функцией Н(у), которая показывает изменение плотности воздуха с изменением высот. Чем меньше будет плотность воздуха, тем меньше будет и сила сопротивления воздуха. Значение Н(у) можно подсчитать по эмпирической формуле профессора В. Ветчинкина: H ( y) 20000 y , 20000 y где у - высота полета снаряда в метрах. Для стрелкового оружия, танковых и артиллерийских орудий при стрельбе прямой наводкой высота полета снарядов бывает очень невелика, поэтому значение Н(у) принимается равным 1. Скорости снаряда. Влияние скорости полета на величину силы сопротивления характеризуется функцией F(v), называемой функцией сопротивления. Для приближенного определения значения F(v) можно пользоваться эмпирическими формулами. При дозвуковых скоростях: F (v) 1,21 10 4 V 2 . При сверхзвуковых скоростях: F (v) V 3 80 . Пример. Определить величину силы сопротивления воздуха для пули обр. 1930 года при V=500 м/с. Решение: H(у)=1; i=0,51; d=0,00762 м. F (v) R 500 80 3 1000 0,51 0,00762 2 1 86,7 9,81 86,7 . 0,261 кг или 261 г. В этом примере сила сопротивления примерно в 22 раза больше веса пули. 84 Ускорение силы сопротивления воздуха. Сила сопротивления воздуха не показывает главного: как быстро будет уменьшаться скорость полета данного снаряда. Возьмем две одинаковые по форме пули, но у одной выплавим свинцовый сердечник. Придадим им одинаковую скорость полета. Сила сопротивления будет одинаковая для той и для другой пули, так как сила сопротивления воздуха не зависит от веса снарядов. (Это видно из формулы R, куда не входит вес снаряда q). Но пули полетят по-разному. Пустотелая пуля быстро потеряет свою скорость и упадет, тогда, как тяжелая пуля будет медленнее терять свою скорость, полетит достаточно далеко, сохраняя большое убойное и пробивное действие. С точки зрения падения скорости на траектории представляет интерес не величина R, а то замедление (ускорение) которое она оказывает на движение снаряда. Ускорение определяется, как отношение действующей силы к массе тела. Следовательно, ускорение силы сопротивления воздуха равно J R , где R m сила сопротивления воздуха; m – масса снаряда. Но масса m q , тогда J g R g . Поставив в это выражение значение q 1000 id 2 H ( y) F (v) и сократив на g, получим: g 1000 id 2 J H ( y) F (v) . q 1000 id 2 Множитель называется баллистическим коэффициентом и обоq R значается буквой С. Тогда окончательное выражение ускорения силы сопротивления воздуха будет: J=C·H(y)·F(v). Анализируя данную формулу, мы видим, что ускорение силы сопротивления воздуха зависит от величины баллистического коэффициента С, плотности воздуха и скорости снаряда. Влияние последних двух факторов уже рассматривалось при анализе формулы, выражающей силу сопротивления воздуха. Поэтому более подробно остановимся на выяснении роли баллистического коэффициента. Баллистический коэффициент объединяет в себе влияние размеров, формы и веса снаряда, т. е. он дает полную характеристику его полетным качествам. 85 Из формулы видно, что чем меньше баллистический коэффициент С, тем меньше ускорение силы сопротивления, тем медленнее снаряд теряет свою скорость. Пример. Определить величину ускорения силы сопротивления воздуха для легкой и тяжелой пуль при скорости их полета 500 м/с. Решение. Баллистические коэффициенты равны: для легкой пули С=3,68 и тяжелой С=2,51; H (у)=1; F(v)=86,5. По формуле J=C·H(y)·F(v) определяем величину ускорения силы сопротивления для обеих пуль. а) Для пули обр. 1908 г. J=13,68·1·86,5=306,3 м/с². б) Для пули обр. 1930 г. J=2,51·1·86,5=217,2 м/с². Решенный пример показывает, что при одинаковой скорости полета легкая пуля быстрее теряет свою скорость. Поэтому, начиная с дальности стрельбы 400 метров, тяжелая пуля по баллистическим качествам превосходит легкую пулю, несмотря на то, что начальная скорость тяжелой пули на 65 м/с меньше, чем легкой пули. Это положение, учитывают стрелки-спортсмены и снайперы: для стрельбы на дальности, превышающие 400 метров, они выбирают тяжелую пулю. Величина баллистического коэффициента обратно пропорциональна весу снаряда. Это значит, что из двух снарядов одинаковой формы и одного и того же калибра в баллистическом отношении более выгоден снаряд большего веса. Для сравнения баллистических свойств снарядов разного веса, но имеющих одинаковые коэффициенты формы, можно пользоваться величиной, выражающей отношение веса снаряда к площади его поперечного сечения, поперечной нагрузкой. Чем больше поперечная нагрузка, тем лучше баллистические качества снаряда. Например, у 7,62-мм тяжелой пули (обр. 1930 г.) поперечная нагрузка составляет 25,9 кг/см², у пули легкой (обр. 1908 г.) – 21,1 кг/см². Отсюда следуют и известные лучшие баллистические качества тяжелой пули. У крупнокалиберных пуль поперечная нагрузка достигает 36,0 кг/см², а у артиллерийских снарядов - нескольких сотен кг/см². Величины баллистических коэффициентов некоторых пуль приведены в следующей таблице № 8. Таблица № 8. Баллистические коэффициенты. Наименование пуль 14,5-мм пуля 7,62-мм пуля обр. 1908 г. 7,62-мм пуля обр. 1943 . 7,62-мм пистолетная пуля 9,00-мм пистолетная пуля Значения «С» 1,60 3,68 4,10 9,50 13,00 Примечание: значения С даны для закона сопротивления воздуха Сиаччи. Действие силы сопротивления воздуха на продолговатый снаряд. 86 При стрельбе из огнестрельного оружия длительное время применялись круглые пули и шаровые снаряды, у которых центр тяжести (ЦТ) и центр сопротивления (ЦС) находились в одной точке, а именно, в геометрическом центре этих тел. При таком положении сила сопротивления всегда направлена в сторону, противоположную направлению полета, и действие ее сводится только к уменьшению скорости движения. Однако, ввиду плохой обтекаемости и малой поперечной нагрузки, шаровые снаряды быстро теряют свою скорость, и дальность их полета невелика. Поэтому уже с середины XIX века производились опытные стрельбы продолговатыми снарядами. К концу XIX века эта работа повсеместно закончилась введением на вооружение продолговатых пуль и снарядов. Продолговатые снаряды имеют большую поперечную нагрузку и, следовательно, большую дальность полета. Однако при такой конструкции центр тяжести не совпадает с центром сопротивления, который находится впереди ЦТ. Рассмотрим, как действует в этом случае сила сопротивления воздуха на продолговатый снаряд. Если бы сила сопротивления воздуха действовала строго вдоль оси снаряда, то ее действие на снаряд сводилось бы только к замедлению скорости полета. В действительности ее действие значительно сложнее. Уже к моменту вылета, вследствие неуравновешенности и перекоса снаряда, а также вследствие того, что в период последействия давления газов на донную часть снаряда, его ось отклоняется от направления полета, образуя с касательной к траектории угол, называемый углом нутации (δ). Это отклонение оси снаряда может произойти в любую сторону случайно (рис. 37 а). Таким образом, сила сопротивления воздуха действует не вдоль оси снаряда, а под некоторым углом к ней. Рис. 37. Образование угла нутации. Для выяснения действия силы сопротивления воздуха приложим к центру тяжести снаряда две взаимно уравновешивающие силы R΄и R˝, равные по величине силе R и противоположные по направлению (рис. 38). 87 Таким образом, действие силы R, приложенное в центре давления заменяется действием R´ в центре масс и момента М пары сил R" и R´ относительно центра масс. При этом R´ - создает сопротивление в поступательном движении, а момент М стремится опрокинуть снаряд. У М Z Рис. 38. Схема действия силы сопротивления воздуха на снаряд. 4.4. Движение вращающегося снаряда в воздухе Стабилизация полета снаряда понимается как решение следующих двух задач: - придание снаряду такой устойчивости, чтобы он не опрокидывался в воздухе; - достижение такого полѐта, при котором бы снаряд «следил» осью за траекторией. Обе эти задачи решаются приданием снаряду вращательного движения. Чтобы правильно уяснить полет вращающихся снарядов, напомним особые свойства вращающихся тел - гироскопов. (Гироскопом называется всякое быстро вращающееся симметричное тело; простейшим гироскопом является обыкновенный волчок). Первое свойство гироскопа. Вращающееся тело способно сопротивляться воздействию внешних сил, сохранять положение оси. Рассматривая это свойство, необходимо отметить, что способность вращающихся тел сохранять положение оси велика и тем больше, чем больше скорость вращения. С помощью гироскопов подаются команды привода которые стабилизируют положение орудийных башен кораблей, танковых пушек, БМП-2, БМП-3, БМД-2, БМД-3, БТР-80У, БТР-90. Устойчивость вращающихся тел можно показать на ряде простых опытов. Заведенный обыкновенный волчок во время вращения не падает, сохраняя положение своей оси вертикально. Еще нагляднее это свойство демонстрируется на специальном приборе - учебном гироскопе. Уравновесим гироскоп на нитке (рис. 39). После этого нанесем по нему небольшой удар, гироскоп сразу 88 изменит положение своей оси. Заведя же гироскоп, можно убедиться, что даже довольно резкие удары не могут отклонить ось гироскопа от первоначального положения. Рис. 39. Учебный прибор-гироскоп. Если учесть, что скорость вращения снаряда во много раз превосходит скорость вращения гироскопов, станет понятно, на сколько велика устойчивость его в полете. Второе свойство гироскопа. При воздействии на гироскоп внешней силы его ось отклоняется в ту сторону, где окажется получившая импульс точка через 3/4 оборота. Отклонение будет тем больше, чем сильнее действие внешней силы. (Сила, с которой ось гироскопа поворачивается под прямым углом к действующей силе, настолько велика, что в практике наблюдались случаи срыва подшипников валов гребных винтов пароходов при резкой килевой качке). Это свойство можно также продемонстрировать на учебном гироскопе. Заведем уравновешенный гироскоп и потянем вниз за нитку, привязанную к оси гироскопа. Ось гироскопа отклонится на 90˚ в сторону его вращения. Если внешняя сила будет действовать на гироскоп постоянно, то его ось будет описывать конус. Это движение называют медленным коническим движением или прецессией. Так вращается ось заведенного на столе волчка (рис. 40). Как увидим дальше, вращается под воздействием силы сопротивления воздуха продолговатый снаряд. Это же движение можно заметить на опыте с гироскопом. Гироскоп, сохраняя горизонтальное положение, своим свободным концом будет описывать конус вокруг точки опоры. Вращающаяся пуля или снаряд являются очень сильными гироскопами. Рассмотрим на основе свойств гироскопа полет в воздухе вращающихся снарядов. 89 а) Полет снаряда на начальном, прямолинейном участке траектории и при стрельбе вертикально вверх и вниз. Рассматривая вращательное движение снаряда, траекторию обычно делят условно на начальную (прямолинейную) часть и криволинейную часть. При движении на прямолинейном участке траектории, а также при Рис. 40. Прецессионное движение оси волчка. стрельбе вверх и вниз, вследствие образования угла δ, на снаряд начнет действовать опрокидывающий момент. Пусть в первый момент снаряд отклонится головной частью вверх. Тогда воздух будет давить на его нижнюю часть. Снаряд вследствие свойств гироскопа не опрокинется, а отклонится головной частью вправо. Теперь воздух будет давить на левый бок снаряда, но снаряд повернется головной частью вниз, и воздух будет давить на верхнюю часть снаряда, в результате чего он отклонится влево. Так как действие воздуха будет непрерывным, то ось снаряда будет описывать конус (рис. 41). Такое движение снаряда называется прецессией. б) Полет снаряда на криволинейном участке траектории. На криволинейном участке касательная к траектории все время понижается. Это приводит к тому, что снаряд будет получать больший импульс снизу, чем со всех других сторон. Следовательно, головная часть снаряда будет больше отклоняться вправо и вниз, чем влево и вверх. Рис. 41. Прецессионное движение снаряда. 90 Проследим подробно один виток прецессионного движения на криволинейном участке траектории. Пусть первоначально головная часть была выше касательной к траектории. Получив импульс силы снизу, снаряд отклонится головной частью вправо и получит давление на левый бок. Вследствие этого он отклонится головной частью ниже касательной к траектории. Но к этому времени снаряд опустится на какую-то величину и касательной к траектории. Угол δ будет значительно меньше, чем он был в тот момент, когда головка снаряда была выше касательной к траектории. Следовательно, снаряд получит меньшее давление на верхнюю сторону относительно оси и только немного отойдет головной частью левее касательной к траектории. А раз так, то он получит небольшой толчок по правому боку относительно оси и снаряд не сможет занять первоначального положения. Ось его после этого витка будет находиться ниже первоначального. Но к этому времени снова опустится касательная к траектории. Угол δ в верхнем положении будет снова большим и снаряд, резко отклонившись вправо, начнет новый цикл, в результате которого его ось опять не возвратится в прежнее положение по высоте. Так, вылетевший снаряд постепенно поворачивается в воздухе головной частью вниз. Для достижения такого правильного полета нужна определенная скорость вращения снаряда. При малой скорости вращения снаряд опрокидывается, при большой скорости вращения мы можем получить «перестабилизрованный» снаряд, который не следит головной частью за траекторией. Так летел бы вращающийся снаряд в безвоздушном пространстве (рис. 42). В артиллерийской практике очень долгое время подбирали опытным путем крутизну нарезки, пока профессор Н.А.Забудский не вывел формулу определения необходимой скорости вращательного движения для придания устойчивости снаряду. Рис. 42. Схема полета вращающегося снаряда в безвоздушном пространстве. 91 Таким образом, вращательное движение не дает опрокинуться снаряду и заставляет его следить за траекторией (рис. 43). Вращательное движение позволило добиться правильности полета снаряда в воздухе. Однако вращающиеся пули и снаряды отклоняются от направления стрельбы в сторону вращения. Это явление отклонения снаряда в сторону вращения от плоскости стрельбы называется деривацией. Деривация — вредное явление, осложняющее стрельбу. Однако величина деривации очень мала по сравнению с дальностью стрельбы и легко может быть учтена с помощью специальных таблиц. В некоторых образцах вооружения деривация устраняется при помощи устройств, установленных в прицел. Они при установке прицела смещают мушку в противоположную сторону от угла деривации (например, ГП-25). Рис. 43. Схема полета стабилизированного снаряда в воздухе. Чтобы уяснить причины деривации, необходимо вспомнить, что при движении на криволинейном участке траектории снаряд больше отклоняется своей осью вправо и вниз, чем влево и вверх. Большее отклонение вправо приводят к тому, что на боковую поверхность снаряда с левой стороны приходится большее сопротивление воздуха и, следовательно, сила Rn (рис. 44) больше действует вправо, отклоняя снаряд вправо от направления первоначального полета. Чем круче будет траектория и больше время полета, тем больше будет и деривация. Угол деривации Rn + Rn Рис. 44. Возникновение деривации. 92 При стрельбе вверх и вниз, а также на небольшие дальности, где траекторию можно принять за прямую линию, деривации нет, так как снаряд будет равномерно прецессировать вокруг касательной к траектории. Сила Rn будет равномерно действовать во все стороны и отклонения снаряда от плоскости бросания не будет. Таким образом, причинами деривации являются: - вращательное движение снаряда; - сопротивление воздуха; - понижение касательной к траектории. При стрельбе из артиллерийских орудий величину деривации учитывают при подготовке данных, внеся соответствующие поправки в исходную установку угломера по таблицам стрельбы. 4.5. Особенности полета не вращающихся снарядов Основным фактором, вызывающим сопротивление воздуха при полете снарядов со скоростями меньшими скорости звука, является образование завихрений. Исходя из этого, минам придают каплевидную форму. Такая форма позволяет при сравнительно небольшой начальной скорости достигать больших дальностей стрельбы. Стабилизация полета мины достигается обычно специальным устройством ее хвостовой части. Как уже было указано, стабилизация полета снаряда должна обеспечить: во-первых, полет его без опрокидывания; во-вторых, обеспечить, чтобы снаряд следил осью за траекторией. Обе эти задачи у мин, гранат решаются установкой стабилизатора, при этом центр тяжести снаряда находится впереди центра сопротивления (рис. 46). При таком расположении центра тяжести и центра сопротивления мина при полете не опрокидывается, и сохраняет устойчивое положение, при полете двигаясь головной частью вперед. Рассмотрим несколько подробнее действие силы сопротивления на мину. Конструкция мины (форма и стабилизатор) приводят к смещению центра сопротивления за центр масс. Схема действия сил аналогична снаряду (рис. 45). М М΄ 93 Рис. 45. Схема действия сил сопротивления воздуха на мину. Сила R´ вызывает сопротивление поступательному движению и момент М от пары R´, R˝ опрокидывает мину. Для устойчивости движения мины необходимо компенсировать М. Таким образом, мина в полете совершает колебательные движения относительно касательной к траектории. Так же, как при рассмотрении действия силы сопротивления на снаряд, приложим к центру тяжести силы и разложим по касательной к траектории и по нормали к ней. У реактивных снарядов, движущихся под действием реактивной силы и после вылета из канала ствола (после схода с направляющих), скорость продолжает увеличиваться до тех пор, пока реактивная сила остается больше силы сопротивления воздуха. Участок траектории ОА от дульного среза (от конца направляющей) до точки, где прекращается действие реактивной силы, называется активным участком, а дальнейшая часть траектории называется пассивным участком (рис.46). Наибольшая скорость снаряда (Vmax) оказывается в конце активного участка траектории. Протяженность активного участка зависит от времени горения боевого заряда, т. е. от продолжительности действия реактивной силы. Этот участок у современных реактивных снарядов наземной артиллерии невелик и обычно не превышает 150 м. При максимальных скоростях реактивных снарядов до 300 400 м/с время полета их на активном участке траектории составляет 0,5 - 0,9 с. Например, если принять скорость движения снаряда на активном участке траектории ускоренной, то при Vmax=400 м/с и длине активного участка S= 150 м время полета будет равно: t S ; Vср Vср 0 400 2 200 м с ; t 150 200 0,75с . Рис. 46. Траектория полета реактивного снаряда. За такое время полета понижение снаряда над линией бросания будет очень незначительным (менее 4 метров), поэтому траектория снаряда на активном участке близка к прямой линии. 94 Пассивный участок траектории АС (рис. 46) ничем не отличается от траекторий обычных снарядов. Так как максимальные скорости реактивных снарядов обычно не превышают скорости звука, основным фактором, вызывающим силу сопротивления воздуха, для них является не баллистическая волна, а образование завихрений. Этим объясняется форма современных реактивных снарядов, напоминающих форму мин, или цилиндр со сравнительно мало заострѐнной головной частью и удлиненной хвостовой частью. Устойчивость в полете реактивным снарядам придается путем оперения их хвостовой части. Центр сопротивления воздуха этим переносится назад за центр тяжести. Действие силы сопротивления воздуха на снаряд при этом аналогично действию на обычную мину. Для улучшения устойчивости некоторым реактивным снарядам придают в полете медленное вращение за счет истечения части газов, через боковые сопла, отклоненные от оси снаряда или приданием наклона перьям стабилизатора, что приводит к повышению кучности боя. Некоторые типы реактивных снарядов не имеют хвостового оперения. Стабилизация их полета достигается быстрым вращением (турбореактивные снаряды), за счет наклона сопел. 4.6. Общие свойства траектории снаряда в воздухе Траектории снарядов в воздухе характеризуются следующими свойствами (рис. 47): • траектория вращающегося снаряда представляет собой несимметричную кривую двоякой кривизны; траектория полета мины - плоская кривая, так как при полете мины отсутствует деривация; • угол падения по своей абсолютной величине больше угла бросания; • скорость снаряда в точке падения меньше начальной скорости; • восходящая ветвь траектории длиннее и настильней нисходящей; • время полета снаряда от точки вылета до вершины меньше времени полѐта от вершины до точки падения; • угол наибольшей горизонтальной дальности для стрелкового оружия меньше 45˚ и колеблется в пределах от 30˚ до 35˚; для дальнобойных артиллерийских орудий от - 55˚ до - 65˚. Для решения практических задач, связанных со стрельбой, внешняя баллистика установила уравнения траектории полета снаряда в воздухе. Эти уравнения очень сложны и представляют собой систему нескольких уравнений Кроме них установлен ряд эмпирических выражений уравнения траектории полета снаряда в воздухе. Можно привести в пример одно из приближенных уравнений траектории в воздухе, сходное по виду с известным нам уравнением траектории в безвоздушном пространстве. Оно имеет следующий вид: y x tg 0 gx 2 2V02 Cos 2 95 1 KV02 X [10], 0 где К - эмпирический коэффициент. Рис. 47. Траектория полета вращающегося снаряда в воздухе. Добавляемый в уравнение для траектории полета снаряда в воздухе сомножитель 1 KV02 X показывает большее (чем в пустоте) понижение снаряда под линией бросания. Следовательно, траектория имеет большую крутизну и меньшую дальность при прочих одинаковых условиях со стрельбой в пустоте. Коэффициент К определяется опытной стрельбой, при которой находится полная горизонтальная дальность Хс. 4.7. Табличные условия. Влияние метеорологических условий на полѐт снаряда Для достижения определенной дальности стрельбы стволу оружия необходимо придать угол возвышения. Величина этого угла зависит от целого ряда причин: расстояния до цели, начальной скорости, веса снаряда, его баллистического коэффициента, состояния атмосферы и т. д. Влияние всех этих факторов при стрельбе учесть одновременно не возможно. Поэтому, рассчитывая прицелы для оружия, допускают, что величина угла прицеливания зависит только от дальности стрельбы. Все остальные величины учитываются поправками относительно нормальных условий стрельбы. За нормальные (табличные) условия стрельбы приняты следующие условия: метеорологические, топографические, баллистические. Метеорологические: • температура воздуха 15˚С; • давление воздуха 750 мм ртутного столба (100 кПа); • относительная влажность воздуха 50%; • ветер отсутствует. Топографические: • цель находится на горизонте оружия, угол места цели не более 15˚; 96 • отсутствует боковой наклон оружия, техники. Баллистические: • вес снаряда и начальная скорость равны значениям, указанным в таблицах стрельб; • температура заряда 15ºС; • оружие первой категории; • оружие приведено к нормальному бою; • форма снаряда соответствует чертежу. При стрельбе в этих условиях установка прицела соответствует величине прицельной дальности. Например, если произвести выстрел с установкой прицела соответствующей дальности в 1000 м, то снаряд пересечет линию прицеливания на удалении 1000 м от точки вылета (рис. 48 а). Если какие-то условия стрельбы будут отличаться от нормальных, то установка прицела не будет соответствовать величине прицельной дальности и в нее, при необходимости, следует вносить соответствующую поправку (рис. 48 б). Возникает потребность учета отклонений условий стрельбы от нормальных и внесения поправок в исходные установки для стрельбы. Рассмотрим основные факторы, которые вызывают те или иные отклонения снарядов, и основные правила внесения поправок при стрельбе. Влияние плотности воздуха. Значительное влияние на дальность полета снаряда оказывает плотность воздуха, которая увеличивает или уменьшает сопротивление воздуха. Плотность воздуха зависит от его температуры, атмосферного давления и влажности. Рис. 48. Зависимость дальности стрельбы от метеорологических условий: 97 а) при нормальных условиях табличная установка прицела соответствует прицельной дальности стрельбы; б) при отклонении условий стрельбы от нормальных установка прицела не соответствует прицельной дальности. Чем выше температура воздуха, тем меньше его плотность и, следовательно, меньше сила сопротивления воздуха. Поэтому с повышением температуры снаряд полетит дальше. И, наоборот, чем ниже температура, тем больше плотность воздуха, тем ближе полетит снаряд при всех прочих равных условиях. Поправки в установку прицела на температуру воздуха вносят с помощью специальных таблиц, помещенных в наставлениях, руководствах по образцам оружия и в таблицах стрельбы ГРАУ. Приведем решения нескольких практических задач с помощью этих таблиц. Пример 1. Дальность до цели 800 м. Определить установку прицела для стрельбы из ручного пулемета РПК74, если температура воздуха равна минус 25°С. Решение. По таблице 19 ТС 61 ГРАУ находим, что на 10° изменения температуры воздуха дальность полета изменится на 18 метров. Так как за нормальную температуру принята температура +15ºС, следовательно, температура отклоняется от нормальной на 4 десятка, а пуля не долетит на 72 метра. Чтобы попасть в цель, необходимо увеличить прицел примерно на 100 метров и стрелять с прицелом 9. Пример 2. Дальность до цели (противотанковое орудие) — 3000 м. Определить установку прицела для стрельбы из 120-мм миномета осколочнофугасной миной, если температура воздуха равна минус 35°С. Решение. В таблице стрельбы ТС 104 ГРАУ для дальности 3000 м находим, что на 10°С отклонения температуры мина изменяет дальность полета на 21 м. Так как фактическая температура отличается от табличной на пять десятков градусов, то мина даст недолет на 105 метров. В соответствии с этим необходимо увеличить установку прицела. Атмосферное давление. Атмосферное давление представляет собой вес воздушного столба атмосферы на единицу поверхности земли. Поэтому понятно, что с повышением над поверхностью земли атмосферное давление уменьшается. С увеличением атмосферного давления плотность воздуха увеличивается, и следовательно, увеличивается сила сопротивления воздуха. Это приводит к недолету снарядов. С понижением давления уменьшается плотность воздуха, уменьшается сопротивление, и снаряды имеют большую дальность полѐта. За нормальное атмосферное давление принято давление, равное 750 мм ртутного столба на высоте 110м над уровнем моря. С увеличением высоты над уровнем моря на каждые 100 метров давление падает на 8 - 9 мм ртутного столба. 98 Для стрелкового оружия при стрельбе на равнинной местности поправки на изменение давления воздуха не учитываются. В горных условиях, при высоте над уровнем моря 1000 и более метров, можно считать, что дальность полета пуль в пределах действительного огня возрастает по сравнению с табличной на 50м - 100 м. Величины поправок на изменение давления приводятся в таблицах стрельбы. Пример 1. Определить установку прицела для стрельбы из 30-мм автоматической пушки БМП на дальность 1800 м, если высота над уровнем моря 1000 метров (определена по горизонталям на карте). Решение. БМП-2 находится на высоте 1000 метров над уровнем моря, т. е. на 10 сотен метров выше табличной высоты. Так как на каждые 100 метров давление понижается на 8 - 9 мм (возьмем 9 мм) то общее понижение давления равно 90 мм, т. е. 9 десятков. По таблице № 43 [9] находим, что на каждые 10 мм давления снаряд изменяет дальность полета на 7 метров. Следовательно, общая величина перелета составит 63 метра. Для минометов при подготовке исходных данных по карте или другими более точными способами поправки на изменение давления воздуха следует учитывать. Эти поправки также приводятся в таблицах стрельбы. Пример 2. Определить установку прицела для стрельбы из 82-мм миномета осколочной миной, если дальность стрельбы 1500 метров, а высота позиции над уровнем моря равна 1300 метров. Решение. Огневая позиция на 12 сотен выше табличной высоты. Следовательно, понижение давления составит примерно 100 мм ртутного столба. По таблице ТС 104 ГРАУ находим, что на каждые 10 мм изменения давления мина изменяет дальность полета на 5 м. При изменении давления на 100 мм ртутного столба дальность стрельбы изменяется на 50 м. Прицел надо назначать, исходя из дальности до цели, уменьшенной на 50 м. Влияние влажности воздуха. В воздухе всегда находится какое-то количество водяных паров. Плотность водяных паров меньше плотности сухого воздуха. (Плотность сухого воздуха при температуре 0˚С и давлении 760 мм ртутного столба равна 1,293 кг/м³, а плотность водяных паров при тех же условиях 0,805 кг/м³). Поэтому при повышении влажности воздуха его плотность уменьшается, что увеличивает дальность полета снарядов. Однако воздух может быть насыщенным водяными парами только до определенного предела, называемого пределом насыщения. Если количество водяных паров будет больше предела насыщения, то вода выпадает в виде тумана или капелек росы, дождя. Когда воздух насыщен водяными парами до предела, говорят, что насыщение равно 100%. 99 Отношение фактически содержащихся в воздухе водяных паров к тому количеству паров, которое необходимо для полного насыщения воздуха называется относительной влажностью. Изменение влажности воздуха очень мало изменяет дальность полета снарядов. Поэтому влажность воздуха учитывается только при проведении опытных стрельб для составления таблиц стрельбы, нормальной относительной влажностью считается влажность 50 %. Влияние ветра. Ветер оказывает значительное влияние на полет снарядов. Это влияние тем больше, чем больше скорость ветра и меньше вес, и скорость снарядов. В зависимости от скорости ветра различают слабый ветер (до 2 м/с), умеренный (4 - 6 м/с) и сильный (8 - 10 м/с) . Ветер может быть попутным, встречным, направленным под углом к плоскости стрельбы. Влияние продольного ветра на движущийся снаряд сводится к изменению сопротивления воздуха, вследствие изменения скорости снаряда по отношению к атмосфере: при попутном ветре сопротивление воздуха уменьшается, при встречном увеличивается. Неверно представлять себе действие, например, попутного ветра на снаряд как «подталкивание» снаряда. Ветер имеет скорость гораздо меньшую, чем снаряд, не может даже «догнать» снаряд, так что о подталкивании не может быть и речи. Таким образом, при попутном ветре сопротивление воздуха уменьшается, а поэтому дальность полета снарядов увеличивается; при встречном ветре дальность полета уменьшается. При стрельбе из артиллерийских орудий, особенно на средние и большие дальности, продольный ветер оказывает существенное влияние на дальность полета снаряда. Например, поправка дальности на продольный ветер со скоростью 10 м/с для минометов, стреляющих только навесным огнем, сказывается на все дальности стрельбы весьма существенно. Например, табличные поправки на продольный ветер со скоростью 10 м/с. составляют: для 82-мм мин на заряде втором около 60 - 80 м, на заряде третьем - от 84 до 120 м; для 120-мм миномета на зарядах пятом и шестом 100 и более метров. На малые дальности стрельбы влияние продольного ветра сказывается несущественно, поэтому в практике стрельбы из стрелкового оружия поправки на встречный и попутный ветер не вводятся. При стрельбе из снайперского оружия поправка учитывается. Наиболее существенным из всех метеорологических факторов, влияющих на полет снарядов, мин и пуль, является боковой ветер. Боковой ветер отклоняет снаряды в сторону от плоскости стрельбы, причем отклонения могут достигать даже при умеренном ветре значительных величин. Поправки на 100 боковой ветер приводятся во всех наставлениях по стрелковому оружию и в таблицах стрельбы ГРАУ. Если ветер дует под острым углом к направлению стрельбы, то для определения поправки на ветер необходимо найти боковую его составляющую, для этого скорость ветра необходимо умножить на синус угла между направлением ветра и плоскостью стрельбы (рис. 49). Приближенные значения синусов можно взять из следующей таблицы. Таблица № 9. Таблица значения синусов угла между направлением ветра и плоскостью стрельбы Величина угла направления ветра Значение синусов 30º 0,5 45º 0,7 60º 0,9 Получив значение боковой составляющей, по таблицам определяют величину поправки. Пример. Определить поправку на боковой ветер при стрельбе из 82-мм миномета на заряде первом по пулеметному расчету, если дальность до цели 900 м, ветер слева со скоростью 10 м/с, под углом 30° к плоскости стрельбы. Решение. Находим боковую слагаемую ветра, для чего умножаем скорость ветра на синус угла в 30°, равный 0,5. Wz =10· 0,5=5 м/с. По таблице стрельбы для 82-мм БМ находим, что поправку необходимо ввести левее на 15 делений угломера. Для стрелкового оружия поправку на угол ветра можно брать приближенно, считая, что при косом ветре она равна половине табличной. 101 Рис. 49. Продольная и боковая составляющие ветра. При сокращенной и полной подготовке стрельбы из артиллерийских систем производится точный учет направления ветра по его дирекционному углу. Направление и скорость ветра определяются и передаются в артиллерийские части артиллерийскими метеорологическими станциями. 102 Глава.V Форма траектории еѐ практическое значение 5.1. Виды траекторий и их применение При стрельбе из любого образца оружия с увеличением угла возвышения от 0° до 90º горизонтальная дальность сначала увеличивается до определенного предела, а затем уменьшается до нуля (рис. 50). 103 Рис.50. Поражаемая зона и наибольшие горизонтальные и прицельные дальности при стрельбе под различными углами возвышения. Угол возвышения, при котором получается наибольшая дальность, называется углом наибольшей дальности. В таблице №10 приведены величины наибольших горизонтальных и прицельных дальностей при различных углах возвышения на примере пули для патрона обр. 1908 г. [12]. Таблица № 10. Величины наибольших горизонтальных и прицельных дальностей при различных углах возвышения. Углы возвышения 1 10º 1 15º 104 2 20º 2 25º 3 30º 3 35º 4 40º 4 45º Наибольшая горизонтальная дальность, м Наибольшая прицельная дальность, м 2 3 3 2670 3040 3200 3370 2 3 3 2670 3040 3200 3370 3 3 3 3 3 3440 3450 3400 3300 3 3 3 3 1 3440 3450 3400 1550 Из таблицы №10 видно, что наибольшая горизонтальная дальность для данной пули будет при угле возвышения 35º; в дальнейшем с увеличением угла возвышения эта дальность начинает заметно уменьшаться. Рис. 50 графически поясняет эту таблицу. Рассматривая график, легко заметить, что при угле возвышения в 45º прицельная наибольшая дальность резко уменьшается, а затем снова постепенно возрастает. Угол наибольшей дальности делит все траектории на два вида: на траектории настильные и навесные. Настильными траекториями называют траектории, получаемые при углах возвышения, меньше угла наибольшей дальности (рис. 51, траектории 1 и 2). Навесными траекториями называют траектории, получаемые при углах возвышения, больше угла наибольшей дальности (рис. 51, траектории 3 и 4). Сопряженными траекториями называют траектории, получаемые при одной и той же горизонтальной дальности двумя траекториями, одна из которых настильная, другая - навесная (рис. 51, траектории 2 и 3). Рис. 51. Угол наибольшей дальности. Настильные, навесные и сопряженные траектории. Данные виды траекторий имеют существенные особенности при их боевом использовании. При стрельбе настильными траекториями с увеличением угла возвышения горизонтальная дальность увеличивается, при стрельбе навесными траекториями, наоборот, - уменьшается. Поэтому при стрельбе навесными и настильными траекториями необходимо иметь различную нарезку шкалы прицела. Настильные и навесные траектории имеют также и различное тактическое применение. Настильные траектории позволяют хорошо поражать открыто расположенные и быстро движущиеся цели, успешно вести стрельбу из орудий и автоматических гранатометов по напольным стенкам ДЗОТ, ДОТ и каменных 105 построек. Однако настильными траекториями не поражаются цели, находящиеся в различных укрытиях (в оврагах, за высотами, строениями и т. д.). Навесные траектории дают хорошую возможность поражать цели за укрытиями и в глубоких складках местности, а также разрушать потолочные перекрытия сооружений. Применение навесных траекторий для поражения открыто расположенных и движущихся целей дает значительно меньший эффект (по сравнению с настильными траекториями), так как время полета снаряда по навесной траектории значительно больше времени полета снаряда на эту же дальность по настильной траектории. Например: при стрельбе из 30-мм автоматического гранатомета на станке АГС-17 на дальность 1000 метров навесной траекторией граната летит 27 секунд; при настильной же стрельбе время полета гранаты на эту же дальность было бы почти в четыре раза меньше (7 с). Эти различные тактические свойства настильных и навесных траекторий нужно учитывать при организации системы огня (рис.52). Необходимость поражать в бою самые различные по своему характеру и степени укрытия цели, потребовала на вооружение армии оружия, предназначенного для ведения огня настильными траекториями (стрелковое оружие, пушечная артиллерия), так и оружия для ведения навесного огня (минометы, гаубицы, станковые и подствольные гранатометы). Рис. 52. Применение навесных траекторий. Наибольшее применение в стрелково-артиллерийской практике имеют настильные траектории. Но и они не всегда одинаковы по форме. Одни из них наиболее отлоги, другие наиболее крутые. Об отлогости траектории судят по величине превышения ее над линией прицеливания или по еѐ высоте, а также по величине угла падения при одной и той же дальности стрельбы. Различные виды оружия можно сравнивать по отлогости их траектории при стрельбе на одинаковые расстояния, но с различными начальными скоростями. Так, например, при стрельбе из 30-мм автоматической пушки 2А42 осколочно-фугасным снарядом на 1000 м высота траектории 1,6 м; при стрельбе из 100-мм орудия-пусковой установки 2А70 осколочно-фугасным снарядом 106 на эту же дальность высота траектории 21 м . На примере видно, что траектория снаряда, выпушенного из 30-мм автоматической пушки, более отлога, чем траектория снаряда 100-мм орудия-пусковой установки (рис 53). V0=286м /с V0=960м /с Рис. 53. Сравнение отлогости траекторий при стрельбе на одинаковые дальности с разными начальными скоростями. Чем отложе траектория, тем больше участок поражения вертикальных целей, тем меньшее влияние на поражение цели оказывают ошибки в определении расстояний. Поэтому при конструировании противотанковой артиллерии, танковых пушек, а также стрелкового оружия стремятся к тому, чтобы траектории этих видов оружия были как можно более отлогими. Средствами к увеличению отлогости траектории могут служить увеличение начальной скорости и улучшение других баллистических качеств снарядов (пуль). 5.2. Прицельное поражаемое пространство Для того чтобы попасть в цель, находящуюся на каком-то определенном расстоянии, например, 700 м, необходимо установить прицел, соответствующий этому расстоянию, и навести оружие в цель. При правильно выбранной установке прицела средняя траектория пройдет через цель (рис.54, траектория с прицелом 7).Если стреляющий при измерении расстояния допустит ошибку в меньшую сторону на 100 м, то стрельба будет вестись с прицелом 6. В этом случае средняя траектория пересечет линию прицеливания ближе цели на 100 м, и пули будут падать в точке Д. Цель не может быть поражена средней траекторией (рис. 54, траектория с прицелом 6). 107 Рис. 54. Возможности поражения целей отлогими траекториями. Д- дальность до цели Если стреляющий при определении расстояния ошибся в большую сторону на 100 м, и будет вести огонь по цели с прицелом 8, то средняя траектория пересечет линию прицеливания в 100 м за целью. Но так как цель имеет некоторую высоту, то она может быть поражена средней траекторией, если превышение траектории в районе цели будет меньше высоты данной цели. Цель высотой 1,6 м при стрельбе из пулемѐта ПКМ будет поражаться средней траекторией, так как на 700 м с прицелом 8 превышение траектории равно 1,6 м (рис.54, траектория с прицелом 8). Таким образом, в силу отлогости траектории создаются условия, при которых вертикальные цели могут быть поражены на некотором протяжении по линии прицеливания, где средняя траектория не поднимается выше цели данной высоты. Этот участок является поражаемым пространством по линии прицеливания. Прицельным поражаемым пространством (Ппп) называется расстояние по линии прицеливания, на протяжении которого нисходящая ветвь траектории не поднимается выше цели данной высоты. Глубина прицельного поражаемого пространства зависит от высоты цели (Вц) и отлогости траектории. Рассмотрим зависимость глубины Ппп от высоты цели (рис. 55). Из рисунка видно, что чем выше цель, тем больше глубина прицельного поражаемого пространства. В нашем примере: для цели 1 глубина Ппп равна отрезку бс; для цели 2 глубина Ппп равна отрезку ас. Следовательно, при стрельбе на одну и ту же дальность из одного и того же оружия глубина Ппп будет тем больше, чем больше высота цели. На рис. 56 видно, что угол падения для пули обр. 1908 г. при стрельбе из ротного пулемета ПКМ на дальность 400м меньше, чем при стрельбе из автомата Калашникова на эту же дальность пулей обр.1943 г. Отсюда и разная величина поражаемого пространства по цели одной высоты. С увеличением дальности стрельбы из одного и того же оружия глубина прицельного поражаемого пространства уменьшается для одной и той же цели. Это понятно из характера изменения угла падения: с увеличением дальности стрельбы угол падения увеличивается, а значит, уменьшается глубина прицельного поражаемого пространства. Например, при стрельбе из 30-мм пушки 2А42 бронебойнотрассирующим снарядом по цели высотой 2 м на дальности 1100м мы будем 108 иметь поражаемое пространство на всем протяжении линии прицеливания от пушки до цели (точка прицеливания – середина нижнего обреза цели). а б с Рис. 55. Зависимость Ппп от высоты цели: а – ростовая фигура, б – поясная фигура, с – точка падения. С увеличением дальности стрельбы до 1400м угол падения увеличивается до 0,7º, а глубина поражаемого пространства по этой же цели уменьшается до 170 м. С увеличением дальности стрельбы до 1800 м угол падения увеличивается до 1º, а глубина поражаемого пространства уменьшается до 100 метров. Рис. 56. Зависимость Ппп от угла падения (отлогости траектории). При стрельбе снизу вверх, сверху вниз, когда углы места цели меньше 15°, считают, что углы прицеливания для достижения одинаковых наклонных дальностей, точно также и углы падения не зависят от углов места цели (начало жесткости траектории). Исходя из этого, можно полагать, что величина прицельного поражаемого пространства не зависит от угла места цели, если величина последнего не более ±15º. Причины, от которых зависит величина прицельного поражаемого пространства, позволяют сделать важные практические выводы. В бою и на учениях с боевой стрельбой огонь необходимо открывать в тот момент, когда цель имеет наибольшие размеры (стоит во весь рост, совершает перебежку, танк или орудие находится на открытой огневой позиции); для поражения далеко отстоящих целей применять оружие, имеющее большую отлогость траектории, т. е. то, которое будет иметь большую величину прицельного поражаемого пространства. Глубина прицельного поражаемого пространства рассчитывается одним из следующих способов. 109 а) По таблицам превышений траектории над линией прицеливания. Для большей наглядности разберем сущность этого способа на примере. Пример 1. Определить глубину прицельного поражаемого пространства при стрельбе из КПВТ бронебойно-трассирующей пулей по БТР противника высотой 2,4 м на дальности 1200м. Решение. По таблицам стрельбы находим, что превышение траектории с прицелом 12 на 1000м равно 2,3 м, что ниже высоты цели. Следовательно, прицельное поражаемое пространство будет более 200м (Ппп=12001000=200м). Пример 2. Определить глубину прицельного поражаемого пространства при стрельбе из СВД по залегшей пехоте (высота цели 0,5м) на дальности 600м. Решение. По таблице превышения средних траекторий находим, что превышение траектории с прицелом 6 на дальности 500м равно 0,74м. Следовательно, изменению дальности от 600 до 500м, т.е. на 100м, соответствует изменение превышения траектории на 0,74м. Составим пропорцию: отсюда X : 100 X 0,5 : 0,74; 100 0,5 0,74 67,57 м. Таким образом, Ппп = 67,57м. б) По углу падения. Этот способ определения величины прицельного поражаемого пространства применяется при условии, что высота цели не превышает 1/3 высоты траектории. В этом случае конечную часть траектории можно без особых погрешностей принять за прямую линию. Рис. 57. Определение прицельного поражаемого пространства (Ппп). Из прямоугольного треугольника АВС (рис. 57) видно, что прицельное поражаемое пространство (катет ВС) определяется по формуле тысячной: 110 Ппп Bц 1000 . c Из формулы видно, что глубина прицельного поражаемого пространства (Ппп) равна высоте цели (Вц), умноженной на 1000 и деленной на угол падения (Θс). Пример 1. Определить глубину прицельного поражаемого пространства при стрельбе из 30-мм автоматической пушки 2А42 бронебойнотрассирующим снарядом по БТР противника высотой 2,7м на дальности 1800м. Угол падения согласно таблицам стрельбы равен 0-17. Решение. Подставим значение угла падения и высоты цели в формулу, получим: 2,7 1000 2700 158,8 м. 17 17 Пример 2. Определить прицельное поражаемое пространство при стрельбе из РПК74 по грудной фигуре (высота цели 0,5м) на дальности 600м. Решение. По основной таблице для РПК74 находим, что угол падения на дальности 600 м равен 0-08,9. Тогда Ппп Ппп 0,5 1000 8,9 500 8,9 56 м. в) По коэффициенту поражаемого пространства. Для быстрого вычисления прицельного поражаемого пространства при стрельбе из стрелкового оружия пользуются специальными таблицами с подсчитанным коэффициентом поражаемого пространства (К). Коэффициентом поражаемого пространства называют отношение 1000 к углу падения: К 1000 . с Чтобы определить прицельное поражаемое пространство этим способом, необходимо высоту цели умножить на коэффициент поражаемого пространства: Ппп=Вц·К. Пример. Определить глубину прицельного поражаемого пространства при стрельбе из пулемета ПКМ по головной фигуре (высота цели 0,3 м) на дальность 600 м. Решение. По основной таблице находим, что коэффициент поражаемого пространства на дальность 600 м равен 100. Подставив значение коэффициента поражаемого пространства и высоты цели в формулу, получим: Ппп = 0,3·100 = 300 м. 111 Следует иметь в виду, что коэффициентом поражаемого пространства так же, как и формулой можно пользоваться только в тех случаях, когда высота цели меньше 1/3 высоты траектории на данном прицеле. Прицельное поражаемое пространство имеет очень большое практическое значение, так как компенсирует ошибки в измерении расстояний и ошибки в стрельбе из-за не учета метеорологических условий. В конечном итоге прицельное поражаемое пространство в некоторой степени компенсирует все ошибки, допускаемые при выборе прицела, в том числе ошибки, связанные с необходимостью округлять установку прицела до 50 - 100 метров. Учитывая, что Ппп компенсирует только ошибки, допущенные при измерении расстояния в большую сторону (при наводке оружия под цель), измеренную до цели, дальность необходимо округлять в большую сторону до 50 100 метров. В пределах участка Ппп цели могут поражаться с одной установкой прицела. Чем больше глубина Ппп, тем в большей степени видны его положительные качества. Поэтому лучшим оружием настильного огня считается то, у которого при прочих равных условиях стрельбы больше величина прицельного поражаемого пространства. Разумеется, в практике боевых действий и учений с боевой стрельбой никогда не приходится заниматься расчетом величины прицельного поражаемого пространства. Приведенные примеры и решаемые при обучении стрелковые задачи помогают сознательно уяснить значение поражаемого пространства и его размеры для типичных случаев стрельбы. На основе этих знаний в боевых условиях командиры и стрелки могут эффективнее и рациональнее использовать своѐ оружие, правильно строить систему огня. 5.3. Дальность прямого выстрела Если бы траектория имела вид прямой линии, то не нужно было бы измерять расстояние до цели и устанавливать соответствующий прицел. Для того чтобы поразить цель, достаточно было бы совместить нулевую линию прицеливания с целью – направить ствол оружия в цель. Однако траектория полета снаряда представляет собой кривую линию и поэтому решение задачи представляет собой определенные трудности. Но все же если мы ведем стрельбу на такие дальности, когда вершина траектории не поднимается выше цели данной высоты, криволинейность еѐ не оказывает влияния на результат стрельбы (рис. 58). Дальностью прямого выстрела называется наибольшая прицельная дальность, при стрельбе на которую средняя траектория не поднимается выше высоты данной цели. При стрельбе из одного и того же оружия дальность прямого выстрела рассматривается относительно каждой конкретной цели, исходя из еѐ высоты. Чем больше высота цели, тем больше дальность прямого выстрела. 112 Рис. 58. Прямой выстрел. Так, например, дальность прямого выстрела при стрельбе из автоматической пушки 2А42 равна: по цели высотой 2 м БТ снарядом 1100 м, а по цели высотой 3 м этим же снарядом - 1300 м. Дальность прямого выстрела зависит, кроме высоты цели, также и от отлогости траектории. Чем отложе траектория, тем больше дальность прямого выстрела. Например. Дальность прямого выстрела по грудной фигуре при стрельбе из АК74 - 440м, из РПК 74 - 460м, из ПКМ - 420м, из СВД - 430м. Различия эти объясняются тем, что траектория указанных пуль имеет различную отлогость, которая зависит от начальной скорости пули. Дальность прямого выстрела определяется путем сравнения высоты цели с высотой траектории при стрельбе с данной установкой прицела. Пример. Определить дальность прямого выстрела при стрельбе из 30 мм автоматической пушки 2А42 БТ снарядом по БТР противника высотой 2,7 м. Решение. По таблицам стрельбы находим, что высота траектории при стрельбе с прицелом 12 равна 2,33 м, а с прицелом 14 – 3,55 м. Следовательно, для цели высотой 2,7 м дальность прямого выстрела больше 1200 м и меньше 1400 м. Точнее можно определить следующим образом. При изменении дальности на 200 м высота траектории изменяется на 1,1 м (3,55-2,45=1,1 м); при изменении дальности на Х м высота траектории изменяется на 0,25 м (2,7-2,45=0,25 м). Составим следующую пропорцию: 200 1,1 x ; 0,25 X 200 0,25 1,1 46 м. Следовательно, дальность прямого выстрела будет равна 1246 м (1200+46=1246 м). Практическое значение прямого выстрела состоит в том, что он дает возможность поражать цели в пределах своей дальности с одной установкой прицела, что особенно важно, когда цель быстро приближается к стреляющему (танки, бронетранспортеры и другие бронецели, вертолеты, пикирующие самолеты и т. д.). 113 Каждый стрелок, автоматчик, пулеметчик, артиллерист и танкист должен знать величину дальности прямого выстрела по различным целям из своего вида оружия. Особое значение имеет стрельба на дальности прямого выстрела из стрелкового оружия и вооружения боевых машин по различным целям. На дальности прямого выстрела строятся наиболее действительные виды огня. Например, кинжальный огонь из пулеметов ПКМ рассчитан на дальность прямого выстрела по грудной цели - 420 м; фланговый огонь пулеметов рассчитан на дальность прямого выстрела по бегущей цели - 640 м. Зоны сплошного огня перед передним краем обороны, а также перед второй позицией строятся с учетом дальности прямого выстрела из индивидуальных образцов стрелкового оружия (ручной пулемет, автомат). При выборе открытых огневых позиций для вооружения боевых машин исходят из того, чтобы они могли успешно вести борьбу с легко бронированными целями противника в пределах дальности прямого выстрела. 5.4. Элементы траектории у точки встречи До сих пор рассматривали свойства и элементы траектории без учета характера местности в районе цели и характера самой цели, по которой ведется огонь. Вполне естественно, что характер цели и местности, на которой расположена данная цель, оказывают значительное влияние на действие снарядов и пуль по целям, затрудняя или облегчая выполнение поставленной огневой задачи. Для более детального изучения этих факторов необходимо рассмотреть элементы траектории у точки встречи. Точкой встречи (С) называется точка пересечения траектории с поверхностью цели (преграды) или земли (рис. 59). Расстояние от точки вылета до точки встречи называется действительной дальностью. Рис. 59. Элементы траектории у точки встреч. Угол, образованный касательной к траектории в точке встречи и касательной к поверхности цели (преграды, земли) в той же точке, называется углом встречи (μ). 114 Угол встречи не может быть больше 90°, и при попадании снаряда (пули) в преграду за угол встречи (μ) - принимается меньший из углов от 0° до 90°. Величина угла встречи значительно влияет на пробивное действие снарядов. Это необходимо учитывать, добиваясь при стрельбе по бронированным целям или различным преградам угла встречи, близкого к 90˚ (рис. 60). Рис. 60. Зависимость пробивного действия снарядов от угла встречи: 1- при малых углах; 2- при больших углах встречи. От величины угла встречи зависит и осколочное действие мин и снарядов по живой силе. На рис. 61 видно, что чем больше угол встречи, тем больше осколочное действие по живой силе противника. Это положение нашло свое отражение в соответствующих правилах стрельбы из артиллерийских систем, имеющих переменные заряды. Величина угла встречи учитывается и при стрельбе на рикошетах осколочными снарядами. Рис. 61. Направление разлета осколков снарядов и мин при различных углах встречи. При ведении огня из стрелкового оружия по живой силе противника, желательно иметь, возможно, меньший угол встречи пули с поверхностью земли. 115 Рис. 62 дает наглядное представление о том, что с уменьшением угла встречи (угол встречи всегда определяется относительно средней траектории) увеличивается величина площади, на которой может одновременно поражаться глубокая групповая цель. Это следует учитывать при выборе позиции огневых средств. Угол, образованный касательной к поверхности земли в точке встречи с горизонтальной плоскостью, называется углом ската (ω). Условно считают, что если скат обращен к стреляющему (скат встречный) – угол ската положительный; если скат обращен от стреляющего (обратный скат) – угол ската отрицательный. Рис. 62. Положение снопа траекторий при стрельбе по глубокой цели. Угол встречи зависит от величины угла ската и угла места цели. Рассмотрим более подробно эту зависимость. а) Зависимость угла встречи от угла ската. Для выяснения зависимости угла встречи от угла ската рассмотрим три случая стрельбы по местности, имеющей различные углы ската. Для простоты расчетов угол места цели примем равным 0, так как цель находится на горизонте оружия. Скат встречный. Угол встречи (μ) равен сумме углов падения и ската: μ=Θс+ω (рис. 63 а). Скат обратный. Угол встречи равен разности углов падения и ската: μ=Θс-ω (рис. 63 б). Местность совпадает с линией прицеливания (горизонтальная). Угол встречи равен углу падения μ=Θс (рис. 63 в). Таким образом, необходимо сделать вывод о том, что при стрельбе по встречному скату угол встречи оказывается больше угла падения, при стрельбе по обратному скату угол встречи меньше угла падения. 116 В общем виде эту зависимость можно выразить следующей формулой: μ=Θс±ω. Рис. 63 Зависимость угла встречи от наклона местности в районе цели: а) скат встречный μ=Θс+ω; б) скат обратный μ=Θс-ω; в) линия прицеливания параллельна скату μ=Θс. Пример 1. Определить угол встречи при стрельбе из 30-мм автоматической пушки 2А-42 БТ снарядом на дальности 1400 м по цели, расположенной на встречном скате крутизной 3°. Решение. По таблицам стрельбы находим, что угол падения на дальность 1400 м равен 12 тысячным. Угол ската встречный в 3˚ составляет 50 тысячных. Подставив эти значения в формулу, получим: μ=Θс+ω=(0-12)+(0-50)=0-62. Пример 2. Определить угол встречи при стрельбе из пулемета ПКМ на дальность 1000м по обратному скату крутизной в 1˚, если цель на горизонте оружия. Решение. По основной таблице для ПКМ находим, что угол падения на дальности 1000 м равен 31 тысячной. Угол ската в 1˚ равен 17 тысячным. Подставим эти значения в формулу, получим: μ=Θс-ω=(0-31)-(0-17)=0-14. б) Зависимость угла встречи от угла места цели. 117 Для выяснения зависимости угла встречи от угла места цели рассмотрим стрельбу по одному и тому же скату с различными углами места цели. Для простоты построения возьмем горизонтальную местность (ω=0). Цель выше горизонта оружия (угол места цели положительный). Угол встречи равен углу падения минус угол места цели (рис.64а): μ=Θс-ε . Цель ниже горизонта оружия (угол места цели отрицательный). Угол встречи равен углу падения плюс угол места цели (рис.64б): μ=Θс+ε. Рис. 64. Зависимость угла встречи от угла места цели: а) цель выше горизонта оружия; б) цель ниже горизонта оружия. Из анализа рисунков следует вывод о том, что при стрельбе сверху вниз угол встречи увеличивается на величину угла места цели, т.е. отрицательный угол места цели необходимо прибавлять к углу падения и, наоборот, при стрельбе снизу вверх угол места цели уменьшает величину угла встречи. Такая зависимость в общем виде выражается формулой: μ=Θс-(±ε). Общая зависимость угла встречи от угла ската и угла места цели выражается формулой: μ=Θс±ω-(±ε), 118 где знак минус, стоящий перед углом места цели, показывает, что при определении угла встречи по формуле необходимо знак угла места цели менять на обратный. Пример 3. Определить угол встречи при стрельбе из СВД на дальность 900 м по встречному скату, крутизной 1°, если цель ниже горизонта оружия на 11м. Решение. По основной таблице находим, что угол падения на дальности 900 м равен 24 тысячных; угол ската равен 17 тысячным; угол места цели равен 12 тысячным. Угол встречи равен: μ=Θс+ω-(-ε)=24+17-(-12)=53 тыс. Величина угла встречи имеет очень большое значение при рикошетной стрельбе из артиллерийских систем. Эта стрельба является основным видом стрельбы для поражения живой силы и огневых средств, расположенных вне укрытий и в открытых окопах (траншеях), а также на воде. Опыты показывают, что при углах встречи около 20˚ при стрельбе по наземным целям и около 10˚ при стрельбе по целям на воде получается примерно 75 - 80% рикошетных разрывов. При дальнейшем же увеличении угла встречи процент рикошетных разрывов резко падает и стрельба на рикошетах становится недействительной. При углах встречи меньше 2° взрыватель, как правило, не срабатывает и снаряды, отражаясь от преграды, рвутся только при втором или даже при третьем падении. В соответствии с этими соображениями правила стрельбы наземной артиллерии рекомендуют выбирать угол встречи так, чтобы он был не менее 2° и не более 20° при стрельбе по наземным и не более 10° при стрельбе по целям на воде. Пример 4. Определить возможность рикошетной стрельбы из 100-мм орудия - пусковой установки 2А70 осколочно-фугасным снарядом на дальность 3000 м, если по карте определены угол места цели минус 5° и скат обратный 10°. Решение. По таблицам стрельбы находим, что угол падения на 3000 м равен 18°. Подставив в формулу данные, получим: с ( ) 180 10 0 ( 50 ) 130. Угол встречи меньше 20° и больше 2°, следовательно, при этих условиях рикошетную стрельбу вести можно. Если при вычислении угла встречи окажется, что он будет отрицательным, то это означает, что цель находится в прикрытом пространстве и не может быть поражена с данной огневой позиции. С рассмотрения угла встречи, мы вплотную подходим к вопросу боевого использования местности в целях повышения действительности огня по противнику. Следует заметить, что для сознательного уяснения рассмотренной зависимости, решение задач на определение угла встречи необходимо осуществлять с помощью чертежа, а не путем механического применения выведенных формул. 119 5.5. Поражаемое пространство Расстояние на местности, на протяжении которого нисходящая ветвь траектории не превышает высоту цели, называется поражаемым пространством (глубиной поражаемого пространства). Глубину поражаемого пространства (Ппр) можно определить по таблицам превышения траекторий над линией прицеливания путем сравнения превышения нисходящей ветви траектории на соответствующую дальность стрельбы с высотой цели, а в том случае, если высота цели меньше 13 высоты траектории, - по формуле тысячной Ппр Вц 1000 , c где Ппр - глубина поражаемого пространства в метрах; Вц - высота цели в метрах; c - угол падения в тысячных. Пример. Определить глубину поражаемого пространства при стрельбе из ПКМ по пехоте противника (Вц = 1,5 м) на расстояние 1000м. Решение. По таблице превышения средних траекторий над линией прицеливания находим: на 1000 м превышение траектории равно 0, а на 900 м – 2,7 м (больше высоты цели). Следовательно, глубина поражаемого пространства меньше 100 м. Для определения глубины поражаемого пространства составим пропорцию: 100 м соответствует превышению траектории 2,7 м; Х м соответствует превышение траектории 1,5 м; Х или 100 1,5 2,7 Ппр 56 м . Так как высота цели меньше 13 высоты траектории, то глубину поражаемого пространства можно определить и по формуле тысячной. Из таблиц находим угол падения θс = 29 тысячным. Ппр Вц 1000 c 1,5 1000 29 50 м . 5.6. Поражаемое пространство на наклонной местности Рассматривая влияние угла встречи на действительность стрельбы из стрелкового оружия, мы уже указывали, что при организации системы огня в оборонительном бою, особенно в зоне сплошного огня перед траншеями, большое значение имеет правильное использование местности для расположения огневых средств. Рис. 65 дает наглядное представление о том, что пулемет, находящийся у основания высоты, может одновременно поражать пехоту противника на значительно большем по глубине участке местности, чем пулемет, занимающий огневую позицию на крутом скате этой высоты. 120 Глубина участка местности, на котором возможно одновременное поражение глубокой групповой цели средней траекторией, называется поражаемым пространством на наклонной местности и ему дается следующее определение. Рис. 65. Использование настильности траектории. Поражаемым пространством на наклонной местности (Ппр) называется протяжение местности, на которой траектория не поднимается выше цели (рис. 66). Рис.66. Поражаемое пространство на наклонной местности (Ппр). Кроме одновременного поражения глубокой групповой цели, Ппр дает возможность поражать цель, движущуюся в плоскости стрельбы, не меняя точки прицеливания до тех пор, пока цель не выйдет из пределов Ппр. Например, наводчик пулемета ведет огонь по движущейся цели способом огневого нападения. Точкой наводки он избрал отдельный куст (рис. 67). Когда цель подойдет к точке А, наводчик открывает огонь и, не меняя точки наводки, ведет его до тех пор, пока цель не дойдет до точки В, т.е. пока она не выйдет из пределов Ппр. Чем больше будет величина Ппр в подобных условиях, тем большее время цель будет находиться под огневым воздействием, следовательно, вероятность поражения этой цели будет выше. Величина Ппр зависит от высоты цели и величины угла встречи. Поражаемое пространство на наклонной местности тем больше, чем больше высота цели (рис. 67). Например, при стрельбе в одних и тех же условиях величина 121 Ппр при стрельбе по перебегающей пехоте значительно больше, чем при стрельбе по переползающим или залегшим фигурам. Рис. 67. Значение Ппр при стрельбе по целям, движущимся в плоскости стрельбы. Особенно большое влияние на величину Ппр оказывает угол встречи. Чем меньше угол встречи, тем больше величина поражаемого пространства на наклонной местности. Величина Ппр при стрельбе с огневой позиции, расположенной у подошвы высоты (рис. 68), получается большей в результате того, что линия прицеливания идет почти параллельно местности. Угол встречи в этом случае значительно меньше, чем при расположении пулемета на гребне высоты, когда стрельба ведется сверху вниз. Рис. 68. Зависимость поражаемого пространства (Ппр) от высоты цели. В том случае, когда линия прицеливания совпадает с линией местности, глубина поражаемого пространства на наклонной местности будет зависеть только от крутизны траектории и высоты цели. При стрельбе по встречному скату Ппр уменьшается, при стрельбе по обратному скату увеличивается, так как соответственно увеличивается или уменьшается величина угла встречи. При необходимости глубину поражаемого пространства на наклонной местности можно определить графически или по формуле тысячных. Графически глубину поражаемого пространства на наклонной местности определяют следующим образом. В определенном масштабе строят профиль местности и траекторию с данной установкой прицела и заданной точкой 122 наводки. Затем сравнивают высоту цели с превышением траектории над линией местности. Несмотря на сложность построения, этот способ является единственным, когда необходимо проверить наличие Ппр на всем протяжении дальности стрельбы. Необходимо отметить, что аналогичный способ проверки наличия Ппр имеет большое применение при заблаговременной организации флангового огня из пулеметов. Для проверки наличия Ппр рекомендуется высылать в направлении стрельбы одного из пулеметчиков. Наводчик или командир, наблюдая в прицел (рис. 69), могут решить вопрос о том, на всем ли протяжении стрельбы имеется Ппр и в соответствии с этим выбрать способ ведения огня в точку или с рассеиванием в глубину. Рис. 69. Определение наличия Ппр при подготовке огня (Ппр на рисунке заштриховано). Например, пулемет с прицелом 5 наведен в отдельный куст (дальний рубеж флангового огня). При проверке направления стрельбы оказалось, что при удалении пулеметчика на 100, 200, 300 и 400 метров линия прицеливания смотрит соответственно в грудь, пояс, грудь и голову высланного подносчика патронов (рис. 69). Определить, будут ли ростовые фигуры поражаться на всем протяжении средней траекторией, если огонь будет вестись тяжелой пулей? Для решения необходимо сравнить превышение траектории на каждую дальность с прицелом 5 с высотой той части фигуры человека, которая оказалась выше линии прицеливания. Составим таблицу. Таблица № 11. Дальность стрельбы, м Повышение траектории, см Высота части фигуры над линией прицеливания, см 100 30 50 200 60 100 300 70 50 400 50 30 Таблица показывает, что если в данном примере стрельба будет вестись в точку, то атакующая пехота противника на каком-то участке от 400 до 200 м дальности не будет поражаться средней траекторией. Следовательно, огонь целесообразнее вести с рассеиванием в глубину. 123 При необходимости определить глубину Ппр только в районе точки встречи (по нисходящей ветви траектории),можно пользоваться формулой тысячной (рис. 70). Ппр Вц 1000 c Рис. 70. Определение поражаемого пространства Ппр. Вывод этой формулы аналогичен выводу формулы для определения величины прицельного поражаемого пространства. Решим несколько примеров на определение Ппр. Пример 1. Определить поражаемое пространство на наклонной местности при стрельбе из ПКМ на дальность 900м по фигуре, бегущей в плоскости стрельбы на переднем скате крутизной 1°. Решение. По основной таблице определяем угол падения на дальность 900 м, он равен 22 тысячным; высота цели (Вц) равна 1,5м. Определим угол встречи (μ). Угол встречи при стрельбе по встречному скату равен сумме углов падения и ската: c ; 0 22 (0 17) 0 39. Подставив эти данные в формулу, получим: Ппр 1,5 1000 39 38 м . Пример 2. Определить Ппр при стрельбе из пулемета ПКМ по бегущим фигурам за обратным скатом крутизною в 1° на дальности 900 м. Решение. По основной таблице находим, что угол падения на дальность 900 м равен 22 тысячным; угол ската в 1° равен 17 тысячным. Угол встречи равен: : c (0 22) (0 17) 0 05 . Глубина поражаемого пространства на наклонной местности равна: 124 Ппр Вц 1000 Ппр ; 1,5 1000 5 300 м. Из примеров 1 и 2 видно, что если оружие и цель расположены на одинаковой высоте, то при стрельбе по встречному скату глубина поражаемого пространства на наклонной местности уменьшается, при стрельбе по обратному скату глубина поражаемого пространства на наклонной местности увеличивается. В первом случае она равна 38 м, во втором - 300 м. Высота цели в обоих случаях взята одна и та же. При стрельбе по целям различной высоты при одном и том же угле встречи глубина поражаемого пространства на наклонной местности будет тем больше, чем больше высота цели. Из примеров также видно, что при стрельбе по встречному скату поражаемое пространство на наклонной местности меньше прицельного поражаемого пространства, а при стрельбе по обратному скату поражаемое пространство на наклонной местности больше прицельного поражаемого пространства. Следовательно, для увеличения поражаемого пространства на наклонной местности необходимо так располагать оружие, чтобы в районе цели получить наименьший угол встречи; практически добиваются, чтобы в районе цели линия прицеливания была параллельна местности. Подводя итоги рассмотрению вопроса о поражаемом пространстве на наклонной местности, необходимо подчеркнуть, что учѐт Ппр решает две важные задачи стрельбы в боевых условиях: - позволяет одновременно поражать глубокую групповую цель как в процессе прицельной стрельбы, так и при ведении направленного огня для отражения, например, ночных атак; - позволяет длительное время держать под огневым воздействием цели, движущиеся в плоскости стрельбы. Таким образом, роль Ппр можно рассматривать только относительно стрельбы автоматическим огнем или при организации системы огня подразделениями. Сознательное усвоение роли Ппр в повышении действительности огня как отдельных огневых средств, так и огня целых подразделений позволит командиру лучше организовать систему огня для наилучшего использования местности в целях нанесения противнику наибольших потерь. Правильное использование поражаемого пространства на наклонной местности имеет особенно большое значение при организации огня в предвидении ночного боя, когда особенно важно создание сплошных зон огня, непреодолимых для атакующих подразделений противника. В умелом создании сплошных участков Ппр в ответственной полосе огня проявляется искусство командира по боевому использованию местности для наилучшего огневого обеспечения боевых действий своего подразделения. Приведенные расчеты и примеры должны послужить основой для сознательного усвоения важных вопросов боевого применения оружия и умелого использования местности. 125 5.7. Прикрытое и мѐртвое пространство При стрельбе из оружия настильного огня (автоматическое оружие, вооружение боевых машин) на пересеченной местности образуется большое количество прикрытых и мертвых пространств. Прикрытые и мертвые пространства позволяют, с одной стороны, скрытно располагать свои огневые средства и боевую технику, а также производить маневр своих подразделений. С другой стороны, они затрудняют ведение огня по противнику, который также стремится наилучшим образом использовать защитные свойства местности. Наибольших успехов в этом единоборстве на поле боя достигнет тот командир, который лучше знает теорию и практику использования местности. Это положение требует внимательного рассмотрения вопроса об определении и свойствах прикрытого и мертвого пространств. Прикрытым пространством (Пп) называется пространство за укрытием, не пробиваемым снарядом, до точки встречи. Прикрытое пространство создается определенным местным предметом. Поэтому оно рассматривается, как протяжение местности за непробиваемым укрытием, на которую при данных условиях не может упасть ни один снаряд. Это и обеспечивает целям, находящимся в пределах этого пространства, определенную гарантию от поражения огнем противника. Поэтому при дальнейшем рассмотрении прикрытого пространства мы всегда будем рассматривать его как прикрытое пространство по местности. В этом смысле прикрытое пространство по геометрическому построению чертежей и формулам для определения его величины аналогично поражаемому пространству на наклонной местности, с учетом которого определяется и величина мертвого пространства за укрытием. В тех случаях, когда стреляющий, не видя местности за укрытием, затрудняется определить величину ската, считают, что местность за укрытием или горизонтальна или параллельна линии прицеливания, направленной под основание укрытия (рис. 71). В последнем случае угол встречи будет равен углу падения по линии прицеливания. Рис. 71. Прикрытое пространство (Пп). Рассмотрим зависимость прикрытого пространства от различных причин. 126 Величина прикрытого пространства зависит от высоты укрытия, угла встречи и расположения укрытия относительно вершины траектории. Чем выше укрытие, тем больше величина прикрытого пространства и, наоборот, чем ниже укрытие, тем меньше его величина в данных условиях стрельбы (рис. 72). Рис.72. Зависимость прикрытого пространства от высоты укрытия При одинаковой высоте укрытия величина прикрытого пространства будет тем больше, чем меньше угол встречи. И, наоборот, с увеличением угла встречи прикрытое пространство уменьшается (рис. 73). Рис. 73. Зависимость прикрытого пространства ( Пп) от угла встречи. Это положение и используют, когда для обстрела обратных скатов и вообще целей, находящихся за укрытием, применяют более крутые траектории или переходят к стрельбе из оружия навесного огня (гаубицы, минометы, АГС17, ГП-25). Для увеличения угла встречи и, следовательно, уменьшения величины прикрытого пространства выбирают огневые позиции на высотах, крышах домов и т. д. Однако при этом следует учитывать, что увеличение угла встречи приводит к резкому уменьшению поражаемого пространства на наклонной местности. На высоких местах особенно выгодно располагать снайперов и отличных стрелков, так как при стрельбе одиночными выстрелами по отдельным целям поражаемое пространство на наклонной местности не имеет практического 127 значения. Уменьшение же прикрытых пространств позволяет снайперам в больших пределах применять меткий огонь своего оружия. Величина прикрытого пространства во многом зависит от того, на какой части траектории находится данное укрытие. При одинаковой высоте укрытия прикрытое пространство тем больше, чем ближе к оружию находится данное укрытие (рис. 74). Рис. 74. Зависимость глубины прикрытого пространства (Пп) от удаления укрытия. Случай расположения укрытия на восходящей ветви траектории и вообще в непосредственной близости от оружия имеет смысл рассматривать только в связи с необходимостью определять наименьший прицел при стрельбе с закрытых огневых позиций. Рассмотрим способы определения прикрытого пространства на нисходящей ветви траектории при стрельбе из стрелкового оружия и вооружения боевых машин. а) Графически. Графически глубину прикрытого пространства можно определить построением в одном масштабе профиля местности и траектории. При всей сложности данного способа он является наиболее точным и может найти применение при выборе наилучшего места для расположений долговременных сооружений, особенно на пересеченной местности. б) По формуле тысячной. Если укрытие находится на нисходящей ветви траектории и ее можно принять за прямую линию (конечную часть траектории принимают за прямую в том случае, если высота укрытия не превышает 1/3 высоты траектории), то глубину прикрытого пространства можно определить по формуле: Пп Ву 1000 где By - высота укрытия; μ - угол встречи в тысячных. 128 , Пример 1. В направлении стрельбы 14,5-мм пулемета КПВТ имеется гребень, высота которого 10 м. Определить прикрытое пространство, если стрельба ведется на дальность 1500 м (за укрытием местность совпадает с линией прицеливания). Решение. По таблицам стрельбы находим, что угол падения на 1500 м равен 1°24' или 23 тысячным. Подставив данные в формулу, получим: Пп Ву 1000 10 1000 23 435 м . Пример 2. В направлении стрельбы из пулемета ПКМ на дальности 900 м находится каменная ограда высотой 1,5 м. Определить глубину прикрытого пространства, если местность за укрытием повышается. Угол ската равен +3°. Решение. По таблицам стрельбы находим значение угла падения на дальность 900 м, он равен 24 тысячным и, переводя угол ската в тысячные, определим величину угла встречи по формуле: c По формуле Пп Ву 1000 24 51 75тыс. определим величину прикрытого пространства: Пп 1,5 1000 75 200 м. в) По таблицам превышения траектории над линией прицеливания. Данный способ, как и способ определения прикрытого пространства по углам прицеливания, применяется только в тех случаях, когда можно допустить, что линия прицеливания за укрытием на всѐм протяжении параллельна местности за укрытием. Разберем этот способ на примере. Пример. Перед фронтом пулеметного отделения на дальности 300 м находится разрушенная кирпичная ограда сада высотой 0,7 м. Определить величину прикрытого пространства, образуемого оградой сада. Решение. Для того чтобы перебросить пули через укрытие (стенку), необходимо выбрать такой прицел, при стрельбе с которым на дальность 300 м превышение траектории над линией прицеливания было бы несколько больше или равно высоте укрытия. Пользуясь таблицей, находим, что такое превышение соответствует прицелу 5 (превышение на 300 м с прицелом 5 равно 0,75 м). Прицел 5 соответствует прицельной дальности 500 м. Следовательно, Пп=500-300=200 м. Ясно, что с данной огневой позиции пулемет не сможет эффективно вести огонь по противнику, поэтому ее необходимо сменить. г) По углам прицеливания. Данный способ рассмотрим также на примере. Пример. В направлении стрельбы пулемета ПКМ имеется укрытие высотой 0,8 м. Дальность до укрытия 400 м. Найдем величину прикрытого пространства. Решение. Для того чтобы пулю добросить до укрытия, пулемету нужно придать угол прицеливания 7,2 тысячных, а чтобы пулю перебросить через 129 укрытие, необходимо этот угол увеличить на высоту укрытия в тысячных (рис. 75). Следовательно, суммарный угол прицеливания (асум) равен сумме угла прицеливания (α) и угла укрытия (ук). Чтобы вычислить суммарный угол прицеливания, нам нужно найти угол укрытия (ук), который легко вычислить по формуле тысячных Ук= Ву 1000 Ду 0,8 1000 400 2тыс. Рис. 75. Определение величины Пп по углам возвышения (прицеливания ). Суммарный угол прицеливания будет равен: асум = 7,2+2 = 9,2 тыс. По таблице определяем дальность, которой соответствует угол прицеливания, равный 9,2 тысячным. Эта дальность равна 560 м. Следовательно, Пп = 560 — 400 = 160 м. Однако за укрытием есть и другой участок, на котором цель не может быть поражена. Участок прикрытого пространства, на котором цель не может быть поражена при данной траектории, называется мѐртвым (не поражаемым) пространством (Мпр). Величина мѐртвого пространства зависит от высоты цели (чем выше цель, тем меньше Мпр), от высоты укрытия (чем больше высота укрытия, тем больше Мпр) и от угла встречи (чем больше угол встречи, тем меньше Мпр). Мѐртвое пространство находится как разность глубины прикрытого пространства и поражаемого пространства на наклонной местности (см. рис.76): Мпр = Пп — Ппр. Разберѐм на примерах способы определения мѐртвого пространства. 130 Рис. 76. Определение мѐртвого пространства (Мпр). Пример. Стрельба ведется из пулемета ПКМ с прицелом 5 через укрытие высотой 5 м, расположенное на расстоянии 500 м от пулемета. Определить глубину Мпр, если высота цели равна 1,7 м. Решение. По таблице определяем угол прицеливания на дальность 500 м, α=8,6 тыс. Определим угол укрытия: У к= 5 1000 500 10тыс . Суммарный угол прицеливания αсум = 8,6 + 10 = 18,6 тыс. Горизонтальная дальность, соответствующая углу прицеливания в 18,6 тысячных, равна 980 м. Следовательно: Пп = 980 — 500 = 480 м. Определим глубину поражаемого пространства на наклонной местности, принимая за угол встречи угол падения (табличный): Ппр Вц 1000 1,7 1000 8,5 200 м. Глубину мѐртвого пространства определяем, как разность глубины прикрытого пространства и поражаемого пространства по местности: Мпр = Пп - Ппр = 480 – 200 =280 м. Полученные результаты означают, что при данных условиях стрельбы возможно поражение целей высотой 1,7 м, находящихся за укрытием на расстоянии от 280 м и далее. 131 Список литературы: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. Наставление по стрелковому делу. 9-мм специальная снайперская винтовка (ВСС). – М.: Воениздат. С. 41. Наставление по стрелковому делу. 7,62-мм снайперская винтовка Драгунова (СВД). – М.: Воениздат. 1967. с.175. Наставление по стрелковому делу. 7,62-мм пулемету Калашникова (ПКМ, ПКМС, ПКМБ, ПКТ). – М.: Воениздат. 1971. с. 253. Наставление по автомату Калашникова, модернизированному складному с прибором бесшумной стрельбы. – М.: Воениздат. 1986. С. 54-57. Наставление по стрелковому делу. 14,5-мм крупнокалиберный пулемет Владимирова (КПВТ). – М.: Воениздат. 1992. с. 224. Наставление по стрелковому делу. 9-мм специальный автомат (АС). - М.: Воениздат. 1994. С. 40. Наставление по стрелковому делу. Самозарядный пистолет специальный (ПСС). - М.: Воениздат. С.38. Наставление по стрелковому делу. Основы и правила стрельбы.. – М.: Воениздат. 1986. с. 176. Правила стрельбы из стрелкового оружия и боевых машин. – М.: Воениздат. 1992. с. 204. Огневая подготовка. Часть первая. Основы и правила стрельбы. Управление огнем./ Под общей редакцией к. в. н. доцента Семенова Ю.И. –– М.: Воениздат.1978 с. 336. Руководство по 5,45-мм автомату Калашникова (АК74, АКС74, АК74Н, АКС74Н) и 5,45-мм ручному пулемету Калашникова (РПК74, РПКС74, РПК74Н, РПКС74Н). Изд. Второе, стереотипное. – М.: Воениздат. 1984. с. 216. Филатов Н.М.. Краткие сведения об основаниях стрельбы из винтовок и пулеметов. Изд. восьмое.– М.: Воениздат. 1944 с. Handbuch fur Panzerbesatzungen I, mittlere Panzer – Berlin, 1984. Handbuch fur waffentechnische Offiziere. // Teil I und II. – Berlin: 1972. Боеприпасы наземной арттиллерии// учебник ч. 1. Под ред. Селезнева Н.А. и Чекалина П.И. Воениздат. – М.: 1970. с. 248. Schiesen aus Panzern. Lehrbuch. – Berlin. Militarverlag der DDR. – 1987. S. 116-147. Алферов В.В. Конструкция и расчет автоматического оружия. – М.: 1977. Баум Ф.А., Станюкович К.П., Шехтер Е.И. Физика взрыва. - М.: Физматгиз. 1959. Вентцель Д.А. Внутренняя баллистика.– М.: ВВИА им. Жуковского. 1948. Горст А.Г. Пороха и взрывчатые вещества. Изд. 3 перераб. – М.: Машиностроение.1972. С. 146-177. Граве И.П. Внутренняя баллистика. Л.: 1933. 132 22. Граве И.П. Внутренняя баллистика. Пиродинамика. Выпуск II. –– Л.: Артакадемия им. Ф.Э. Дзержинского. 1934. с. 292. 23. Дроздов Н.Ф. Решение задач внутренней баллистики для бездымного пороха трубчатой формы.– М.: Артакадемия. 1941. 24. Дроздов Н.Ф. Решение задач внутренней баллистики для зарядов простых и сложных.– М.: Акад. Арт. Наук. 1950. 25. Ермолова С.И., Слухоцкий В.Е. Таблицы внутренней баллистики. Часть 1. Воениздат. – М.: 1948. 26. Ермолова С.И., Слухоцкий В.Е. Таблицы внутренней баллистики. Часть 2. Воениздат. – М.: 1948. 27. Колтовской А.С. Внутренняя баллистика. 1922. 28. Корнер Дж. Внутренняя баллистика орудий.– М.: Иностранная литература. 1953. 29. Кувеко А.Е. Внутренняя баллистика. К.: КВИАВУ 1969. 30. Серебряков М.Е. Внутренняя баллистика ствольных систем и пороховых ракет.– М.: Гос. Науч.-Тех. Издат. Оборонгиз. 1962. с. 703. 31. Серебряков М.Е. Физический закон горения во внутренней баллистике. М.: Оборонгиз. 1940. 32. Таблицы стрельбы по наземным целям из стрелкового оружия калибров 5,45 и 7,62 мм. Изд. Второе, дополненное, ТС/ГРАУ № 61. – М.: Воениздат. 1977 с. 262. 33. Чурбанов Е.В. Внутренняя баллистика периода форсирования. Учебное пособие 2-е изд. Доп. – СП б.: БГТУ. с. 192. 34. Чурбанов Е.В. Внутренняя баллистика артиллерийского орудия.– М.: Воениздат. 1973. 35. Чурбанов Е.В. Внутренняя баллистика.– Л.: ВАА им. Куйбышева. 1975. 36. Чурбанов Е.В. Внутренняя баллистика. Учебник.– Л.: Артакадемия. 1975. 37. Чурбанов Е.В. Таблицы внутренней баллистики и их применение. Пособие по разделу курса № 111 «Основные сведения из внутренней баллистики». – Л.: 1971. с. 78. 38. Вольф В. Внутренняя баллистика. – Берлин: 1961. С. 94. 39. Оттенхеймер Внутренняя баллистика. Перевод с французского. - 1930. 40. Remmler E. Verbrennungs und Vergasungs. Lehre 2 - Berlin: 1957.s 123. 41. Балаганский И.А. Габдрахманов Р.Х. Расчет внутрибаллистических параметров в системах обратного метания с отсечкой пороховых газов в переменно-замкнутом объѐме.// Материалы Российской научнопрактической конференции «НПО – 2004». – Новосибирск. 2004. С. 5457. 42. Меленис Б.Г. Термическое разложение и горение взрывчатых веществ и порохов.– М.: Наука. 1996 43. Губин С.Г. Исследования тепловых процессов в метательных зарядах с запиранием пороховых газов с целью повышения их эффективности. Диссертационное исследование. НГТУ. с. 147. 133 44. Waffenlehre fur die Bundeswehr. Dathal, H. – Bonn,1972. 45. Jane’s Ifantpy Weapons, Jane’s Publisching, New Jork. USA, 1987-88g.g. s.455-456,464,540. 46. Боевая машина пехоты БМП-2. Техническое описание и инструкция по эксплуатации. Часть I.– М.: Воениздат. 2002. 47. Боевая машина пехоты БМП-3. Техническое описание и инструкция по эксплуатации. Часть I.– М.: Воениздат. 1992. 48. Аманов В.В., Дерюгин Л.М., Чижевский О.Т., Есиев Р.У. Артиллерийский патрон для гранатомета. Описание патента RU 2125226 C1. – 1998. с. 6. 49. Губин С.Г. Боеприпасы для бесшумной, беспламенной и бездымной стрельбы. Сборник научных статей №2. НГТУ.- 2002 С. 50. Попов В.Л., Шигеев В.Б., Кузнецов Л.Е. Судебно-медицинская баллистика. – СПб.: Гиппократ, 2002. С. 83. 51. Хоменко Ю.П., Ищенко А.Н., Саморокова Н.М. Интегродифференциальный метод определения законов горения конденсированных систем в условиях постоянного объема.// Физика горения и взрыва. – 1999. – т.35. - № 1. С. 67-71. 52. Jane’s Ammunition Handbook, Jane’s Publisching, New Jork, USA, 199697g.g., s. 497-503. 53. Староверов А.А., Енейнина Т.А., Газизов Ф.Ф. Пороха к 5,6 мм патрону. // Вопросы специального машиностроения. Сер.2. – №8. –1992. с. 24-25. 54. Петров В.А., Касьянов И.П., Юрьев А.Б., Корнилова Е.С., Медвецкий С.В. Патрон СП- 4. Описание изобретения. – RU 2059189 C1. - 1993. с. 4. 55. Фролов Ю.З., Забелин Н.В., Касьянов И.П., Кирнилова Е.С. Описание патрона типа УС. ЦНИИ Точ. Маш. Патент RU 2079805 C1. – М.: 1962. с. 3. 56. Патент РФ N 2087837, кл. F 42 В 5/02, опубл. 20.08.97 в бюл. №23. 57. Балаганский И.А., Мержиевский Л.А. Действие средств поражения и боеприпасов: Учебник. – Новосибирск: Издательство НГТУ. – 2004. –408 с. – (серия «Учебники НГТУ»). 134 ПРИЛОЖЕНИЯ: Приложение № 1. Таблица № 12. Характеристики инициирующих ВВ. Название ВВ Гремучая ртуть (известна и применяется с 1799 г.) Исходные продукты Ртуть, обработанная азотной кислотой, затем этиловым спиртом Состояние (вид) Кристаллический порошок белого или серого цвета, плотность в гранулах 4,42 Стойкость Стойка до попадания влаги. При 10% влажности и в малых количествах не взрывается, а горит. С металлами (кроме алюминия) не взаимодействует Азид свинца Смесь азида Порошкооб- Стоек, не (применяет- натрия с разное ве- гигроскопися с 1907 г., азотнокисщество бе- чен, легко впервые по- лым свин- лого цвета, реагирует с лучен в 1891 цом плотность медью г.) 4,8 ТНРС (тринитрорезерцинат свинца) Натриевая соль стифниновой кислоты и азотнокислый свинец Порошкообразное вещество желтого цвета, плотность 3,1 Стоек, с металлами не взаимодействует Тетразен (применяется с 1922 г.) Аминогуанидиннитрат, обработанный азотнокислым натрием в нейтральном растворе Мелкокристаллический порошок желтоватого отлива Стоек, в воде не растворим, мало гигроскопичен 135 Чувствительность Очень чувствительная (даже к трению деревянной палочкой). Температура вспышки 160ºС- 165ºС Очень чувствителен (не менее гремучей ртути). Температура вспышки 345ºС Чувствителен к пламени, даѐт сильный луч огня, к удару менее чувствителен. Температура вспышки 276ºС Чувствителен к удару как гремучая ртуть. Температура вспышки 135ºС- 140ºС Применение Для снаряжения капсюлей. Примерный состав капсюля – воспламенителя: 1) гремучая ртуть – 16,7%; 2) бертолетова соль – 55,5%; 3) антимоний – 27-28% Для снаряжения капсюлей, заменяет гремучую ртуть. В место 0,5 г гремучей ртути 0,15-0,2 г азида свинца В азидотетриловых капсюляхдетонаторах для безотказности воспламенения В смеси с ТНРС в ударных составах, заменяет гремучую ртуть Приложение № 2 Таблица № 13. Характеристики дробящих ВВ. Наименование ВВ 1 Исходные продукты Пироксилин Целлюлоза (клетчатка) обработанная азотной кислотой 2 Состояние (вид) Чувствительность Применение 4 5 6 Очень стоек Нечувствителен, можно пилить, дробить Впитывая воду, становится влажным Очень чувствительный к удару, трению, огню Чрезвычайно чувствителен к удару, трению, сотрясению. Температура вспышки 200ºС Стойкость 3 Влажный до 30% влаги Сухой (2-3% влаги) Желтовато-бе лая масса Плотность 1,65 – 1,66 Нитроглицерин Глицерин, обработанный серной и азотной кислотами Маслянистая жидкость, бесцветная или желтоватая, без запаха. Плотность 1,6 Плохо растворим в воде; хорошо в спирте эфире. Сам является хорошим растворителем Тротил (тол) Толуол, обработанный смесью азотной и серной кислот Твердое кристаллическое вещество в виде плавленой массы желтоватого цвета. Плотность 1,66 Очень стоек, в воде не растворим, с металлами не взаимодействует. Реагирует со щелочами Мелинит (плавленая пикриновая кислота) Бензол и фенол, находящиеся в продуктах коксования угля и перегонки нефти Твердое кристаллическое вещество яркожелтого цвета, очень горькое на вкус. Плотность 1,51-1,59 Слабо растворим в воде; с металлами вступает в реакцию и образует опасные соединения - пикраты 136 Не чувствителен к удару (даже пули), от огня горит без взрыва сильно коптящим пламенем. Температура вспышки 290ºС- 295ºС Чувствительность выше чем у тротила в 1,5-2 раза. Температура вспышки около 300ºС Для изготовления бездымного пороха и подрывных шашек Служит детонатором к влажному пироксилину В чистом виде как ВВ не применяется. Применяется для изготовления нитроглицериновых порохов и динамитов Является основным дробящим ВВ для снаряжения боеприпасов, для изготовления подрывных шашек Для снаряжения боеприпасов, преимущественно с динитронафталином 1 2 3 4 5 6 Тетрил Диметиланилин – производное от анилина и метилового спирта Твердое мелкокристаллическое вещество бледно-жѐлтого цвета, без запаха. Плотность прессованного 1,581,63 В воде не растворим. Менее стоек к нагреву, чем тротил и мелинит Значительно более чувствителен к удару, чем мелинит, к удару. Температура вспышки 195ºС- 220ºС В качестве промежуточных детонаторов для различных боеприпасов, в качестве зарядов в капсюляхдетонаторах Гексоген Уротропин, Белое кристалазотная ки- лическое вещеслота ство. Плотность 1,82 Стоек, плавится при 200ºС и при этом разлагается Очень чувствителен к механическим воздействиям. Температура вспышки 230ºС В капсюляхдетонаторах, в сплавах с тротилом для снаряжения снарядов малого калибра; наиболее мощное ВВ ТЭН Пентаэритрит, азотная кислота Стоек, температура плавления 141ºС Очень чувствителен к механическим воздействиям. Температура вспышки 215ºС Для капсюлейдетонаторов, для снаряжения артиллерийских снарядов малого калибра Кристаллическое (порошкообразное) вещество белого цвета. Плотность 1,62 137 Приложение № 3. Таблица № 14. Свойства взрывчатых веществ Название Состав Плотность г 0 см3 Тротил (ТNT) Гексоген (RDX) Октоген (НМХ) ТЭН (PETN) ТАТБ (ТАТВ) Состав В (Comp B) Пентолит Нитроглицерин (NM) Аммиачная селитра (AN) ТА-23 ТГ-20 Окфол 3,5 Пластит ПВВ-12 Пластит ПВВ-5а Пластит (С-4) Эластит ЭВВ-34 Тринитротолуол Циклотриметилентринитрамин Циклотетраметилентетранитрамин Пентаэтрит тетранитрат Триаминтринитробензол Гексген/тротил 64/36 Тротил/ТЭН 50/50 Нитрометан Теплота взрыва Qv кДж/кг 1,06 1,64 1,00 1,80 1,90 3570 4330 5000 5530 5460 1,00 1,77 1,895 5440 5870 1,713 4860 - 1,65 - Показатель изоэнтропы ПД k 1,66 3,16 2,48 2,98 3,00 Скорость стациионарной детонации D, км/с 5,25 6,95 5,98 8,75 9,10 Давление в точке Чепмена Жуге PH, ГПа 11,0 19,0 10,8 34,7 39,3 2,45 2,64 2,72 5,48 8,30 7,86 8,7 33, 31,5 2,76 8,03 29,4 2,84 7,47 24,7 1,128 4640 2,17 6,29 14,1 Нитрат аммония 1,05 1,725 1440 1600 3,21 3,69 4,58 7,68 5,23 21,7 Тротил/Al 77/23 Тротил/гексоген 20/80 Октоген/флегматизатор 96,5/3,5 Гексоген/связка 90/10 Гексоген/связка 85/15 Гексоген/связка 91/9 ТЭН/пластификат ор 80/20 1,73 1,71 5910 5150 - 6,50 8,15 - 1,76 5240 - 8,70 - 1,60 5200 - 8,00 - 1,40 4610 - 7,40 - 1,64 5030 - 8,19 - 1,50 4570 - 7,7 - 138 Приложение № 4 Таблица №15. Ресурс стволов Вид оружия Количество выстрелов 73 мм 2А28 100 мм Т-55 (Д 1072) 125 мм Т-72 (Д 81) 9 мм ПМ 9 мм АПС 5,45 мм ПСМ 7,62 мм СВД 7,62 мм АКМ и его модификации 5,45 мм АК74 и его модификации 7,62 мм ПКМ и его модификации 7,62 мм РПК и его модификации 5,45 мм РПК74 и его модификации 12,7 мм НСВ 14,5 мм КПВТ 30 мм АГС-17 73 мм СПГ-9 40 мм РПГ-7 и его модификации 30 мм 2А42 30 мм 2А72 100 мм 2А70 9 мм АПСБ (АО-44) 1250 900 350 (для подкалиберных –150) 4000 8000 3000 6000 10000 10000 25000 20000 20000 10000 12000 4000 500 250 6000 6000 500 6000 139



