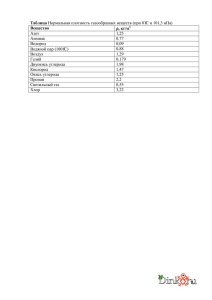
распределение углерода по фракциям фитомассы различных

УДК 630. 181.37
Виктор Александрович Соловьев, доктор биологических наук, профессор,
[email protected]
Чан Тхи Тху Нян, аспирант, [email protected]
Екатерина Владимировна Шорохова, кандидат биологических наук, доцент,
Санкт-Петербургский государственный лесотехнический университет
РАСПРЕДЕЛЕНИЕ УГЛЕРОДА ПО ФРАКЦИЯМ
ФИТОМАССЫ РАЗЛИЧНЫХ ДРЕВОСТОЕВ И ЛЕСНОГО МАССИВА
Запасы углерода, распределение Ципфа–Парето, фракция фитомассы,
древостой.
Stores of carbon, Zipf–Pareto distribution, fraction of phytomass, forest stand.
Изучению фракционного состава фитомассы отдельных деревьев и
древостоев посвящено значительное число работ [8]. Данные такого рода
необходимы для познания очень многих процессов в лесных биоценозах
(фотосинтеза, транспирации, опада и отпада и т. д.), оценки трансформации
экологических факторов (освещенности, температуры, потоков в воздухе и т.д.) в
толще занимаемого древостоями пространства, моделирования биологической
продуктивности древостоев. Данные по фракционному составу полезны для более
полного учета лесных ресурсов, для оценки полноты использования фитомассы
древостоя при лесозаготовках и для обоснования различных лесохозяйственных
мероприятий, направленных на достижение конкретных целей выращивания лесов
разного назначения. Обычно выделяют четыре основных фракции фитомассы
дерева и древостоя: ствол, корни, ветви и листва (хвоя), а для описания связей
между фитомассами различных фракций используют регрессионные уравнения.
При таком подходе неплохо описывается фракционный состав в конкретных
условиях. В поисках закономерностей в связях была выдвинута концепция
инвариантности растительного покрова, т.е. постоянства и независимости
некоторых показателей биогеоценотического процесса от других сильно
изменяющихся показателей (например, таксационных показателей).
Методы исследования. В данной работе использован другой подход,
основанный на социологических законах, выражающих функциональную
зависимость между изучаемыми фактами. Эти законы выражаются
негауссовскими распределениями и часто встречаются в задачах распределения
ресурсов, где требуется максимизация общей полезности – в экономических,
биологических, экологических и политических системах. Простейшим
распределением такого типа является распределение В. Парето (1878-1923). Дж.
Ципф сделал большой вклад в распространения распределения Парето в ранговой
форме на многие явления общественной деятельности. Уравнение Ципфа – Парето
в ранговой форме имеет вид:
m (i) = A . i –(1+α), 0 < xo≤ x, 0 < α < ∞,
(1)
33
где i – номер ранга компоненты (фракции) в ряду, начиная с максимального значения m (i),
m (i) – ресурс, приходящийся на долю i-ого компонента, А- константа, количественно равная
ресурсу, приходящемуся на долю первого компонента, α – константа, определяемая
эмпирически и характеризующая интенсивность процессов взаимосвязей (взаимодействия)
между компонентами; чем больше α, тем больше ресурса приходится на первый по рангу
компонент; чем меньше α, тем длиннее «хвост» распределения (из имеющихся
статистических данных Парето определил α равным 1,4).
Довольно обширный банк данных распределений Ципфа – Парето в самых
различных областях знаний представлен в книгах С. Д. Хайтуна [9,10] и А. И.
Яблонского [12,13]. В.Г. Суховольский использовал уравнение Ципфа – Парето
для описания фракционной структуры и продуктивности фитомассы деревьев и
древостоев [1,4,5,6]. Линеаризируя уравнение (1), получаем:
ln m(i) = a - b.ln i,
(2)
где
a = ln А, b = α+1.
Из уравнения (2) следует, что ранговое распределение ресурса,
приходящегося на фракцию 1 – ствол, 2 – корни, 3 – ветви, 4 – листва (хвоя),
описывается прямой линией в двойных логарифмических координатах ln i - ln
m(i), соответственно можно определить параметры регрессионного уравнения (2)
а и b, используя метод наименьших квадратов.
Для описания распределений углерода по фракциям фитомассы в
различных древостоях и в лесном массиве использовали банк повыдельных
данных
Охтинского
учебно-опытного
лесхоза
Санкт-Петербургского
государственного лесотехнического университета. Запасы углерода в древостое
определяли на основании данных о запасе древесины по повыдельным данным
лесоустройства 2005г. и с помощью конверсионно-объемных коэффициентов,
представляющих собой отношение фитомассы отдельных фракций к запасу
древесины и зависящих от возраста древостоя и преобладающей в нём породы.
Массу коры рассчитывали в зависимости от породы и диаметра [7] ее объем,
умножая на среднюю базисную плотность [3]. Для расчета запаса углерода
древостоя использовали программу, написанную на языке Visual Basic в MS Excel.
Полученные значения запасов углерода по фракциям (в т С.га-1)
представлены в работе Чан Тхи Тху Нян и др. [11]. В данной работе показано
распределение запасов углерода, исходя из уравнения (2).
Результаты и их обсуждение. В качестве иллюстрации некоторых
результатов на рис. 1 показаны регрессионные уравнения распределения углерода
во фракционной структуре фитомассы древостоев в черничных влажных типах
леса. Как видно из рисунка, между фитомассой разных фракций и их рангом в
логарифмических координатах наблюдается довольно тесная линейная связь
(скорректированный на число степеней свободы коэффициент детерминации R2
варьирует от 95,1 до 99,6 %). Наклон прямой характеризуется величиной b,
служащей численной мерой распределения фитомассы по фракциям. Величины b,
рассчитанные по суммарным запасам углерода, равны 2,08 для березняков, 2,06
для сосняков, 1,76 для ельников и 1,68 для осинников. Это значит, что в
березняках и сосняках доминирует стволовая фракция, а в ельниках и осинниках
фитомасса распределяется более равномерно.
34
Сосняки
Ельники
Березняки
Осинники
Рис. 1. Регрессионные уравнения распределения углерода в различных фракциях
фитомассы древостоев черничных влажных типов леса.
Распределение углерода в древостоях различного состава, возраста,
бонитета и типов леса представлено в табл. 1. Как видно из таблицы, логарифмы
запасов углерода мало изменялись в связи с возрастом. За редким исключением
они имели естественную тенденцию увеличиваться с возрастом древостоя. На
величину запасов углерода значительное влияние оказала полнота реальных
древостоев. Из таблицы видно небольшое плавное изменение величины b с
возрастом древостоя – от средневозрастных до перестойных: достижение
максимума в спелых древостоях (в сосняках 2,32, в березняках 2,11) и минимума
(в ельниках 1,51). В осинниках подобная закономерность менее заметна (в
приспевающих 1,89, в спелых 1,66, перестойных 1,77). Данных о молодняках
недостаточно для определения величины b, но в березовых молодняках b = 1,35.
Имеются сведения о том, что с возрастом дерева и древостоя величины b
несколько возрастают и достигают более или менее постоянной величины в
средневозрастных и последующих группах (неопубликованные данные).
Для всех доминантов – эдификаторов представлены данные по изменению
величины b в зависимости от типа леса лишь по зеленомошной группе, мало
различающейся по режиму увлажнения и трофности почв (кисличные, черничные
свежие и черничные влажные). Для сосняков она равна 2,06…2,09, в
долгомошном типе 2,13. Для ельников заметно увеличение b от 0,79 в кисличных
типах до 1,74 в черничных влажных; для осинников, наоборот, уменьшение b от
35
1,69 в кисличных, до 1,47 в черничных влажных типах леса. Незначительное
снижение величины b наблюдается с увеличением застойного увлажнения и
уменьшения трофности для березняков (2,32…2,37 в кисличных и черничных
свежих типах до 2,25…2,32 в травяно-таволговых и приручейных). Практически
же по всему градиенту экологических факторов для березняков сохраняется
величина b равная 2,25…2,37.
Таблица 1
Распределение углерода по фракциям фитомассы древостоев
Количество
Древостой
R2
a
b
выделов
по группам возраста
4,03*
2,06*
99,38*
Сосняки
569
4,05**
2,06**
99,67**
Средневозрастные
343
3,96
1,96
99,94
Приспевающие
101
4,12
2,18
98,51
Спелые
53
4,15
2,32
98,34
Перестойные
72
4,16
2,15
98,72
4,03*
1,77*
91,47*
Ельники
99
4,04**
1,76**
99,42**
Средневозрастные
26
4,20
2,15
90,18
Приспевающие
24
4,08
1,72
99,07
Спелые
39
3,88
1,51
85,64
Перестойные
10
4,04
1,90
99,31
3,84*
2,06*
98,69*
Березняки
677
3,93**
2,09**
98,67**
Молодняки
20
2,38
1,35
98,70
Средневозрастные
38
3,27
1,92
99,34
Приспевающие
64
3,75
2,12
99,02
Спелые
453
3,95
2,11
98,40
Перестойные
102
3,91
2,02
99,54
3,64*
1,70*
95,06*
Осинники
84
3,69**
1,68**
87,32**
Средневозрастные
3
2,11
1,07
99,05
Приспевающие
13
3,75
1,89
99,26
Спелые
48
3,67
1,66
96,00
Перестойные
20
3,72
1,77
89,49
по типам леса
3,90*
2,08*
99,63*
Сосняки
533
4,04**
2,06**
99,58**
Кисличные
126
3,97
2,06
99,69
Черничные свежие
249
3,94
2,09
99,64
Черничные влажные
131
3,84
2,08
99,61
Долгомошные
27
3,59
2,13
99,28
3,50*
1,05*
73,32*
Ельники
87
4,03**
1,76**
98,80**
Кисличные
62
3,50
0,79
63,09
36
Продолжение таблицы 1
3,43
1,67
98,67
3,66
1,74
98,76
3,66*
2,32*
95,50*
Березняки
623
3,93**
2,09**
95,41**
Кисличные
338
3,87
2,32
95,58
Черничные свежие
103
3,83
2,37
95,04
Черничные влажные
64
3,12
2,31
94,79
Травяно-таволговые
65
3,36
2,26
96,06
Приручейные
35
2,86
2,25
96,17
Долгомошные
18
3,13
2,32
95,76
3,69*
1,67*
86,23*
Осинники
75
3,69**
1,68**
87,53**
Кисличные
68
3,72
1,69
85,08
Черничные влажные
7
3,45
1,47
97,40
по классам бонитета
3,96*
2,10*
99,19*
Сосняки
573
4,04**
2,06**
99,67**
1
4
4,29
1,91
99,91
2
5
4,10
1,98
99,94
3
188
4,05
2,10
99,43
4
206
4,02
2,15
98,94
5
131
3,88
2,14
98,97
5а
36
3,41
1,78
99,97
5б
3
3,20
2,07
99,43
4,01*
1,89*
99,00*
Ельники
96
4,03**
1,76**
99,42**
2
9
4,10
1,46
96,81
3
42
4,07
1,80
99,33
4
38
4,02
2,15
99,09
5а
7
3,54
1,62
99,39
3,53*
2,00*
99,14*
Березняки
672
3,92**
2,08**
98,67**
1
7
4,26
2,10
97,84
2
35
4,08
2,12
97,93
3
250
3,80
2,02
98,76
4
318
3,34
1,98
99,56
5
55
2,95
1,94
99,33
5а
7
2,11
1,89
99,92
3,67*
1,67*
87,42*
Осинники
81
3,69**
1,68**
99,58**
2
7
3,84
1,64
91,12
3
51
3,79
1,69
86,20
4
23
3,35
1,65
89,00
Примечание: * - средневзвешенное по выделам значение; ** - рассчитанное по
суммарному запасу углерода.
Черничные свежие
Черничные влажные
18
7
37
Более четко проявляются тенденции к небольшому, по закономерному
изменению величины b по классам бонитета: понижению от 2,10…2,12 (для 1 и 2
бонитета) до 1,94…1,89 (для 5 и 5а бонитета) в березняках, повышению от 1,91
(для 1 бонитета) до 2,15…2,14 (для 4 и 5 бонитета) и вероятному снижению с
ухудшением роста (в 5а и 5б бонитетах) в сосняках.
Представленные величины b присущи Охтинскому лесному массиву.
Различия в величинах невелики, но характерны для древостоев определенной
породы от средневозрастной до перестойной группы возраста. Величина b
приблизительно равна 2,1 для сосняков и березняков и 1,8 для осинников; для
ельников она, по-видимому, зависит от условий местопроизрастания и полноты
древостоя, для них необходимо дополнительное исследование.
Отмеченные закономерности распределения углерода в фитомассе
древостоев по основным фракциям можно использовать для определения массы
каждой фракции при известных а и b по формуле
m(i)= exp (a-b.lni),
где а= ln m(1), m(1) – масса углерода первой по рангу стволовой части фитомассы
(древесина + кора), наиболее легко определяемая эмпирически (в частности, таким путём
можно определять или уточнять массу корней [8]).
Распределение Ципфа – Парето позволяет предположить, что оно отражает
некоторые принципиально важные структурные закономерности, имеющие
отношение и целостности и устойчивости описываемой системы. Замечено, что
оно выполняется по частоте слов для циклов стихов или рассказов, но гораздо
хуже для произведения, состоящего из отдельных частей, например, для романа
[13]. Аналогично распределение фракций фитомассы дерева довольно точно
описывается уравнением Ципфа – Парето и несколько менее точно выполняется
для древостоя и лесного массива. Можно предположить, что в отдельном дереве,
древостое и лесном массиве происходят процессы оптимизации распределения
углерода и фитомассы по фракциям. Эти процессы встречаются часто в задачах
распределения ресурсов, где происходит взаимодействие частей (элементов)
системы и требуется максимизация общей полезности – в экономических,
политических, биологических и экологических системах [6]. Распределение с b=2
называют распределением конкуренции. Оно используется в качестве
приближения даже в тех случаях, когда нет уверенности, что b=2 [2].
Заключение. Охтинский лесной массив представляет собой целостность, в
которой структура фитомассы древесных пород-эдификаторов удовлетворительно
описывается распределением Парето в линеаризированной форме:
ln m(i)= a - b.ln i,
где, m(i) – масса фракции i; i – ранг фракции: 1 – ствол; 2 – корни; 3 – ветви; 4 – листва
(хвоя); а – логарифм стволовой массы (древесина + кора), b – константа распределения
фитомассы по фракциям.
38
В статье приведены значения а и b для Охтинского лесхоза. Величина b
определяется в значительной степени биологическими особенностями древесной
породы и возрастом древостоя. Бонитет практически не влияет на величину b, а
тип леса влияет в малой степени. В условиях Охтинского массива можно принять
величину b равной 2,1 для сосняков и березняков, 1,8 для осинников. Для
ельников она, по–видимому, зависит от условий местопроизрастания и полноты
древостоя. Найденные закономерности позволяют рассчитать массу углерода в
фитомассе дерева, древостоя и лесного массива в целом и по основным фракциям
при известной стволовой массе.
Библиографический список
1. Бузыкин, А.И. Густота и продуктивность древесных ценозов [Текст] / А.И.
Бузыкин, Л.С. Пшеничникова, В.Г. Суховольский. – Новосибирск: Наука, 2002. – 152 с.
2. Подлазов, А.В. Закон Ципфа и модели конкурентного роста [Текст] / А.В.
Подлазов // Нелинейность в современном естествознании. Под ред. Г.Г. Малинецкого. – М.:
Изд-во ЛКН, 2009. – С. 229-256.
3. Полубояринов, О.И. Базисная плотность древесины и коры лесообразующих пород
европейской части России [Текст] / О.И. Полубояринов, А.М. Сорокин, Р.Б. Федоров //
Лесное хозяйство, №2. – Арх.: АрхГУ, 2000. – С. 35-36.
4. Суховольский, В.Г. Оптимизационные модели межпопуляционных взаимодействий
[Текст]/ В.Г. Суховольский, Т.Р. Исхаков, О.В. Тарасов. – Новосибирск: Наука, 2008. – 162 с.
5. Суховольский, В.Г. Процессы свободной конкуренции за ресурс [Текст] / В.Г.
Суховольский // Математические проблемы экологии. – Новосибирск: ИМ СО РАН, 1996. –
С. 151-154.
6. Суховольский, В.Г. Экономика живого. Оптимизационный подход в описании
процессов в экологических сообществах и системах [Текст] / В.Г. Суховольский.–
Новосибирск: Наука, 2004. – 140 с.
7. Тетюхин, С.В. Лесная таксация и лесоустройство: Нормативно-справочные
материалы по Северо - Западу Российской федерации [Текст] / С.В. Тетюхин, В.Н. Минаев,
Л.П. Богомолова. – СПБ: СПбГЛТА, 2004. – 360 с.
8. Усольцев, В.А. Фитомасса лесов Северной Евразии: нормативы и элементы
географии [Текст] / В.А. Усольцев. – Екатеринбург: УрО РАН, 2002. – 762 с.
9. Хайтун, С.Д. Наукометрия: состояние и перспективы [Текст] / С.Д. Хайтун. –
М.: Наука, 1983. – 344 с.
10. Хайтун, С.Д. Количественный анализ социальных явлений: проблемы и
перспективы [Текст] / С.Д. Хайтун. – М.: Ком Книга, 2010. – 277 с.
11. Чан Тхи Тху Нян. Динамика углерода в лесном массиве Охтинского учебноопытного лесхоза [Текст] / Чан Тхи Тху Нян, Е.В. Шорохова, В.А. Соловьев // Известия
Санкт-Петербургской лесотехнической академии: вып. 197. – СПб.: СПбГЛТУ, 2011. – С.
110-120.
12. Яблонский, А.И. Математические модели в исследовании науки [Текст] / А.И.
Яблонский. – М.: Наука, 1986. – 352 с.
13. Яблонский, А.И. Модели и методы исследования науки [Текст] / А.И.
Яблонский. – М.: Эдиториал УРСС, 2001. – 400 с.
39
__________
Охтинский лесной массив представляет собой целостность, в которой структура
фитомассы древесных пород-эдификаторов удовлетворительно описывается распределением
Парето в линеаризированной форме: ln m(i)= a – b.ln I, где, m(i) – масса фракции i; i – ранг
фракции: 1 – ствол; 2 – корни; 3 – ветви; 4 – листва (хвоя); а – логарифм стволовой массы
(древесина + кора), b – константа распределения фитомассы по фракциям. В статье
приведены значения а и b для Охтинского лесхоза. Величина b определяется в значительной
степени биологическими особенностями древесной породы и возрастом древостоя. Бонитет
практически не влияет на величину b, а тип леса влияет в малой степени. В условиях
Охтинского массива можно принять величину b равной 2,1 для сосняков и березняков, 1,8
для осинников. Для ельников она, по–видимому, зависит от условий местопроизрастания и
полноты древостоя. Найденные закономерности позволяют рассчитать массу углерода в
фитомассе дерева, древостоя и лесного массива в целом и по основным фракциям при
известной стволовой массе.
***
Okhtinsky forest represents a system, where the structure of the tree species phytomass is
described by the linearized Pareto equation: ln m(i)= a - b.ln i,where: m (i) – mass of the i-th
fraction; i – rank: 1 – stem, 2 – roots, 3 – branches, 4 – foliage or needles; a – logarithm of the stem
mass (wood + bark), b – constant of the phytomass distribution by fractions. The a and b values
were estimated for Okhtinsky forest. The biological characteristics of the tree species and tree stand
age affected the b value. The b value did not depend neither on the site class (bonitet) nor on the
forest type. This value equaled 2.1 for pine and birch stands and 1.8 for aspen forests. In spruce
forests, b depended on site conditions and stand basal area. Our results allow to calculate carbon
mass and its distributions by fractions in trees, tree stands and forest landscapes based on known
stem mass.
УДК 630*58.114.521.7
Дмитрий Михайлович Киреев, доктор сельско-хозяйственных наук, профессор
[email protected]
Санкт-Петербургский государственный лесотехнический университет
ИНДИКАЦИОННЫЙ МЕТОД ИЗУЧЕНИЯ ЛЕСОВ
Индикационный метод, компонент, элемент ландшафта, дистанционные
методы, формула экологического режима земель.
Indicatory method, component of landscape, element of landscape, remote sensing,
formula of ecological lands regime.
Индикационные методы исследований основаны на взаимосвязи между
явлениями и объектами окружающей нас природы, т. е. между индикаторами и
индикатами.
Отличительной чертой индикатора является его доступность для
непосредственного наблюдения и оценки. Индикатор лежит на поверхности, он
40