Примерные задачи к олимпиаде по информатике для школьников.
реклама

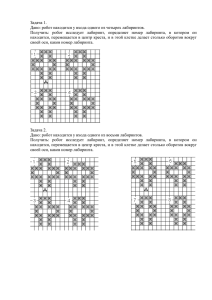
Примерные задачи к олимпиаде по информатике для школьников. 1. Если в некоторой системе счисления десятичное число 47 записывается в виде 52, то чему равно основание этой системы? 2. Как хорошо известно, существует телеграфный код (азбука Морзе), где каждый из передаваемых символов кодируется комбинацией точек и тире. Разные символы кодируются различными по длине последовательностями точек и тире. Символы отделяются друг от друга временной паузой. Например, сигнал SOS передается последовательностью одиннадцати символов: · три точки, · пробел (пауза), · три тире, · пробел (пауза), · три точки. Предложите экономный способ хранения длинного нераскодированного сообщения в виде последовательности байтов. 3. Пусть имеется прямоугольный лабиринт, разбитый на клетки со стороной 1 метр. Длина лабиринта — n метров, ширина — m метров. На плане лабиринта закрашенная клетка соответствует непроходимому препятствию. Высота лабиринта всюду одинакова и равна 3 (трем) метрам. Вход в лабиринт и выход всегда размещены в левом верхнем и правом нижнем углах. Нумерация клеток начинается из левого верхнего угла. Перед открытием сезона необходимо оклеить все внутренние стены лабиринта новыми обоями. Опишите алгоритм определения общей площади всех внутренних стен лабиринта. Входные данные n, m; двухмерный массив (прямоугольная таблица) размерностью n m. Элементы массива принимают одно из двух значений: “пусто” или “занято”. Пример Лабиринт (n = 14, m = 12), карта которого представлена ниже, имеет площадь внутренних стен 104 3 = 312 м2 . Контуры внутренних стен на рисунке выделены жирной линией. 4. Петя загадал 7 целых чисел: от -4 до 4 каждое. Хитрый Коля предложил Пете составить сумму по следующему алгоритму. Первое число умножают на 1, второе на 10, третье на 100, четвертое на 1000 и так далее. А затем эти числа складывают. 1)помогите Коле, зная результат сложения S=-1417169, найти все эти числа; 2)опишите рациональный по времени алгоритм восстановления исходных чисел по известной сумме.