Теория вероятностей - Институт управления, бизнеса и права
реклама
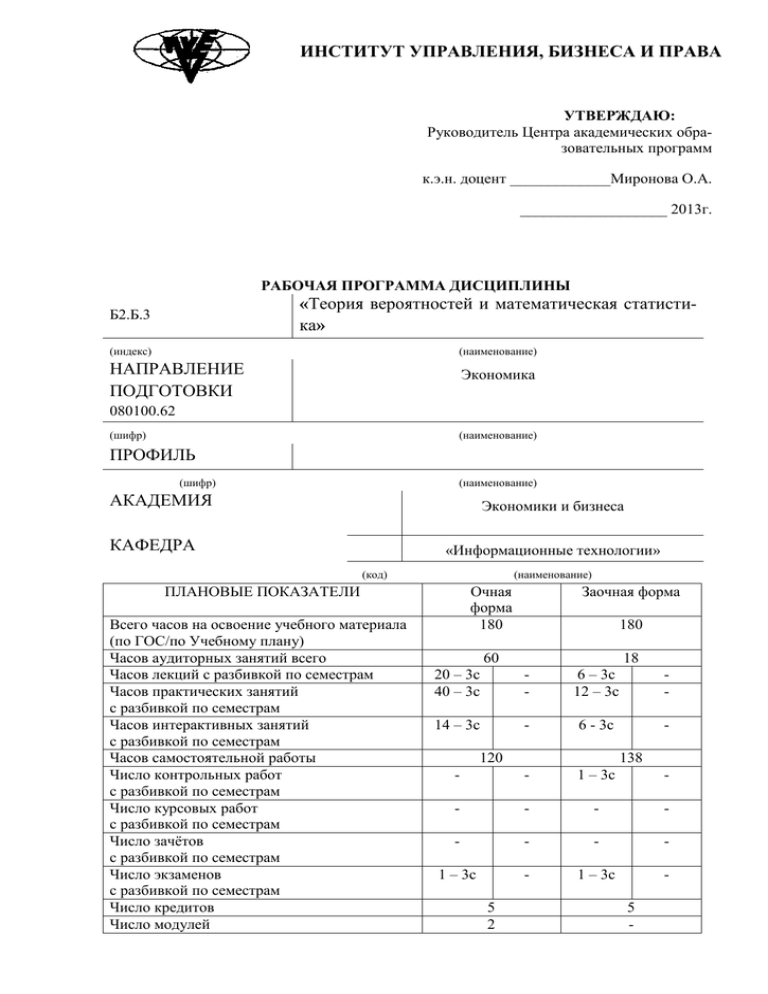
ИНСТИТУТ УПРАВЛЕНИЯ, БИЗНЕСА И ПРАВА УТВЕРЖДАЮ: Руководитель Центра академических образовательных программ к.э.н. доцент _____________Миронова О.А. ___________________ 2013г. РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ Б2.Б.3 «Теория вероятностей и математическая статистика» (индекс) (наименование) НАПРАВЛЕНИЕ ПОДГОТОВКИ Экономика 080100.62 (шифр) (наименование) ПРОФИЛЬ (шифр) (наименование) АКАДЕМИЯ Экономики и бизнеса КАФЕДРА «Информационные технологии» (код) (наименование) ПЛАНОВЫЕ ПОКАЗАТЕЛИ Всего часов на освоение учебного материала (по ГОС/по Учебному плану) Часов аудиторных занятий всего Часов лекций с разбивкой по семестрам Часов практических занятий с разбивкой по семестрам Часов интерактивных занятий с разбивкой по семестрам Часов самостоятельной работы Число контрольных работ с разбивкой по семестрам Число курсовых работ с разбивкой по семестрам Число зачётов с разбивкой по семестрам Число экзаменов с разбивкой по семестрам Число кредитов Число модулей Очная форма 180 Заочная форма 180 60 18 20 – 3с 40 – 3с - 6 – 3с 12 – 3с - 14 – 3с - 6 - 3с - 120 138 - - 1 – 3с - - - - - - - - - 1 – 3с - 1 – 3с - 5 2 5 - Автор рабочей программы Ткачук Е.О. (подпись) (Ф.И.О.) РАБОЧАЯ ПРОГРАММА СОСТАВЛЕНА НА ОСНОВАНИИ: 1. Государственного образовательного стандарта высшего профессионального образования направления подготовки 080100 ЭКОНОМИКА от 21.12.2009г (дата утверждения) 2. Учебного плана направления подготовки 080100 ЭКОНОМИКА (название) 1.07.2013 (дата утверждения) РАБОЧАЯ ПРОГРАММА ОБСУЖДАЛАСЬ И СОГЛАСОВАНА КАФЕДРОЙ: Информационные технологии (наименование) Ткачук Е.О. (подпись зав. каф) Протокол заседания кафедры № 1 от 31.08.2013 УМС Академии управления (наименование) Протокол УМС № 1 Пивоваров И.В. (подпись председателя УМС) от 31.08.2013 (Ф.И.О.) (Ф.И.О.) 1 ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ Цель - формирование у будущих специалистов теоретических знаний и практических навыков по применению вероятностно-статистических методов в работе по специальности. Задачи - реализация требований, установленных в квалификационной характеристике подготовки специалистов по прикладной информатике. - обучение навыкам составления и исследования теоритко-вероятностных моделей, решения математических задач, обработке и анализа экспериментальных данных. 2 ТРЕБОВАНИЯ К УРОВНЮ УСВОЕНИЯ ДИСЦИПЛИНЫ В процессе изучения дисциплины студенты должны: Овладеть компетенциями: Перечень названий и шифров компетенций в соответствии с ФГОС ВПО анализировать и интерпретировать финансовую, бухгалтерскую и иную информацию, содержащуюся в отчетности предприятий различных форм собственности, организаций, ведомств и использовать полученные сведения для принятия управленческих решений (ПК-7); анализировать и интерпретировать данные отечественной и зарубежной статистики о социально-экономических процессах и явлениях, выявлять тенденции изменения социально-экономических показателей (ПК-8); используя отечественные и зарубежные источники информации, собрать необходимые данные проанализировать их и подготовить информационный обзор и/или аналитический отчет (ПК-9). Знать: - основные понятия и методы теории вероятностей и математической статистики; Уметь: - использовать основные приемы обработки экспериментальных данных при решении прикладных задач по специальности; - использовать возможности вычислительной техники и программного обеспечения. 3 3.1 № п/п АУДИТОРНАЯ РАБОТА Лекции Тема лекции 1 Теория вероятностей 2 Основы математической статистики Краткое содержание Лекция 1. Предмет теории вероятностей. Случайные события. Алгебра событий. Относительная частота и вероятность случайного события. Полная группа событий. Классическое определение вероятности. Основные свойства вероятности. Аксиомы теории вероятностей. Зависимость событий. Теоремы сложения и умножения вероятностей. Основные формулы комбинаторики. Лекция 2. Формула полной вероятности и формула Байеса. Схема и формула Бернулли. Приближение Пуассона для схемы Бернулли. Случайные величины. Закон распределения и функция распределения дискретной случайной величины. Лекция 3. Биномиальное распределение и распределение Пуассона. Функция распределения и плотность распределения непрерывной случайной величины, их взаимосвязь и свойства. Равномерное распределение вероятностей. Лекция 4. Основные числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Их свойства и примеры. Нормальное распределение. Лекция 5. Числовые характеристики одномерных случайных величин: начальные и центральные моменты, мода, медиана, квантиль, коэффициенты асимметрии и эксцесса. Двумерные случайные величины Лекция 6. Условные законы распределения составляющих двумерной случайной величины. Равномерное распределение на плоскости. Числовые характеристики двумерных случайных величин Лекция 7. Основные понятия математической статистики. Генеральная совокупность и выборка. Вариационный ряд, статистический ряд. Группированная выборка. Группированный статистический ряд. Полигон частот. Выборочная функция распределения и гистограмма. Числовые характеристики статистического распределения: выборочное среднее, оценки дисперсии, оценки моды и медианы, оценки начальных и центральных моментов. Статистическое описание и вы- Кол. часов О/З 12/4 8/2 № п/п Тема лекции Краткое содержание числение оценок параметров двумерного случайного вектора. Лекция 8. Основные свойства статистических характеристик параметров распределения: несмещенность, состоятельность, эффективность. Несмещенность и состоятельность выборочного среднего как оценки математического ожидания. Асимптотически несмещенные оценки. Способы построения оценок: метод наибольшего правдоподобия, метод моментов, метод квантили, метод наименьших квадратов, байесовский подход к получению оценок. Лекция 9. Корреляционный анализ. Проверка гипотезы о значимости выборочного коэффициента корреляции. Ранговая корреляция. Регрессионный анализ. Однофакторный дисперсионный анализ. Моделирование случайных величин методом МонтеКарло (статистических испытаний). Лекция 10. Непараметрические методы статистики . Критерий Вилкоксона, Колмогорова критерий и Крамера- Мизеса критерий. ИТОГО: 3.2 № п/п 1 Кол. часов О/З 20/6 Практические и лабораторные занятия Тема занятия Теория вероятностей Краткое содержание Непосредственные способы определения вероятностей событий: классический, статистический и геометрический. Косвенные способы определения вероятностей событий. Формула вероятности появления хотя бы одного события. Формулы полной вероятности и Байеса. Основные виды распределений случайных дискретных и непрерывных величин: биномиальное, Пуассона, равномерное, экспоненциальное и нормальное. Вероятности попадания случайных величин в заданные интервалы. Предельные теоремы и приближения биномиального распределения. Схемы повторных опытов. Частная теорема Бернулли. Решение практических задач на ПЭВМ и графическом калькуляторе «Casio» с использованием встроенных и пользовательских функций. Кол. часов О/З 20/2 № п/п Кол. часов О/З Тема занятия Краткое содержание 2 Основы математической статистики Построение и сглаживание эмпирических распределений по выборкам большого объёма. Построение эмпирических распределений по выборкам малого и умеренного объёмов. Сглаживание эмпирических распределений генеральными распределениями значительной общности. 10/6 3 Многомерный статистический анализ Оценивание числовых характеристик случайной величины по выборкам ограниченного объёма. Оценивание коэффициентов корреляции. Оценивание корреляционных отношений по малым выборкам. Проверка линейности уравнений регрессии. 6/2 Построение математической модели экономического явления методом регрессионного анализа. 4 3.3 № п/п 1 Методы непараметрической статистики 4/2 40/12 Интерактивные занятия Тема занятия Краткое содержание и вид интерактивного занятия Определение вероятности Непосредственные способы определения вероятностей событий: классический, статистический и геометрический. Метод кейс-стади (обсуждение конкретных проблемных ситуаций и информации в группе). 4/1 Формулы полной вероятности Косвенные способы определения вероятностей событий. Формула вероятности появления хотя бы одного события. Формулы полной вероятности и Байеса. Метод кейс-стади (обсуждение конкретных проблемных ситуаций и информации в группе). Основные виды распределений случайных дискретных и непрерывных величин: биномиальное, Пуассона, равномерное, экспоненциальное и нормальное. Вероятности попадания случайных величин в заданные интервалы. Метод кейс-стади (обсуждение конкретных проблемных ситуаций и информации в группе). 2/1 2 3 Непараметрические методы точечного и интервального оценивания числовых характеристик признаков. Непараметрические методы проверки статистических гипотез по малым выборкам. ИТОГО: Распределение случайной величины Кол. часов О/З 2/1 № п/п 4 5 Тема занятия Обработка статистических данных Корреляционный анализ Краткое содержание и вид интерактивного занятия Построение и сглаживание эмпирических распределений по выборкам большого объёма. Построение эмпирических распределений по выборкам малого и умеренного объёмов. Метод кейс-стади (обсуждение конкретных проблемных ситуаций и информации в группе). Оценивание числовых характеристик случайной величины по выборкам ограниченного объёма. Оценивание коэффициентов корреляции. Оценивание корреляционных отношений по малым выборкам. Проверка линейности уравнений регрессии. Метод кейс-стади (обсуждение конкретных проблемных ситуаций и информации в группе). ИТОГО: Кол. часов О/З 4/1 2/2 14/6 4 САМОСТОЯТЕЛЬНАЯ РАБОТА Форма контр. № п/п Содержание самостоятельной работы Кол. часов О/З 1 Изучение материала по теме «Теория вероятностей» 20/34 Тест модуля 1 2 Оформление отчётов по результатам выполнения лабораторных работ по теме «Теория вероятностей» Изучение материала по теме «Основы математической статистики» Оформление отчётов по результатам выполнения лабораторных работ по теме «Основы математической статистики» Оформление отчётов по результатам решения задач по темам «Теория вероятностей» и «Основы математической статистики» Изучение материала по теме «Многомерный статистический анализ» Изучение материала по теме «Методы непараметрической статистики» ИТОГО: 24/24 Материалы работ Тест модуля 2 3 4 5 6 7 30/34 16/20 Материалы работ 10/20 Материалы работ 10/15 Реферат 10/15 120/162 5 ТЕМЫ КУРСОВЫХ РАБОТ И УЧЕБНЫХ ПРОЕКТОВ. Не предусмотрены учебным планом. 6 ТРЕБОВАНИЯ К ИТОГОВОЙ АТТЕСТАЦИИ Форма итоговой аттестации: Экзамен Вопросы к экзамену: 1. Понятие события; классификация событий с примерами. 2. Алгебра событий: определения и графическая иллюстрация суммы и произведения событий. 3. Классические методы определения вероятностей событий. 4. Статистический метод определения вероятности события. 5. Геометрический метод определения вероятности события. 6. Зависимость событий, условные и безусловные вероятности. 7. Аксиомы теории вероятностей. 8. Теорема сложения вероятностей для совместных событий. 9. Теорема сложения вероятностей для несовместных событий, следствия из неё. 10. Теорема умножения вероятностей для зависимых событий. 11. Теорема умножения вероятностей для независимых событий. 12. Формула вероятности появления хотя бы одного события. 13. Формулы полной вероятности и Байеса, их значение для практики. 14. Понятие случайной величины; классификация случайных величин с примерами. 15. Ряд и многоугольник распределения дискретной случайной величины, их свойства. 16. Функция распределения случайной величины и её свойства. 17. Плотность распределения случайной величины и её свойства. 18. Определение вероятности попадания случайной величины в заданный интервал с использованием функции распределения и плотности распределения. 19. Математическое ожидание дискретной и непрерывной случайной величины. 20. Характеристики положения случайной величины (мода и медиана). 21. Дисперсия и среднее квадратическое отклонение случайной величины. 22. Начальные и центральные моменты случайных величин; свойства, которые они характеризуют. 23. Биномиальное распределение случайной величины, его характеристики. 24. Распределение Пуассона, его характеристики. 25. Равномерное распределение случайной величины, его характеристики. 26. Нормальное распределение случайной величины, свойства кривой Гаусса. 27. Понятие о центральной предельной теореме и её практических применениях. 28. Вероятность попадания нормально распределённой случайной величины в заданный интервал. Правило “трёх сигм” для нормального распределения. 29. Общее биномиальное распределение. Аппроксимация общего биномиального распределения двойным нормальным распределением. 30. Предмет и основные задачи математической статистики. Примеры генеральных совокупностей и выборок. 31. Существо закона больших чисел (теорем Бернулли и Чебышёва). 32. Построение вариационных рядов распределений по выборкам большого объёма. 33. Вычисление числовых характеристик случайной величины по вариационным рядам распределений. 34. Сглаживание эмпирических распределений генеральными распределениями значительной общности. 35. Понятие статистики. Точечное оценивание числовых характеристик случайной величины по выборке большого объёма. 36. Точечное оценивание числовых характеристик случайной величины по выборке ограниченного объёма. 37. Существо интервального оценивания числовых характеристик случайной величины. Пример для математического ожидания случайной величины. 38. Основные понятия и задачи статистической проверки гипотез. 39. Проверка гипотезы о равенстве математических ожиданий двух совокупностей случайной величины. 40. Проверка гипотезы о равенстве дисперсий двух совокупностей случайной величины. 41. Корреляционная связь. Коэффициент корреляции. 42. Проверка значимости коэффициента корреляции. Двусторонний и односторонний t-тесты. 43. Парная линейная регрессия. Корреляционное отношение. 44. Расчет параметров парной линейной регрессии. Метод наименьших квадратов. 45. Проверка гипотез о значимости коэффициентов корреляции. 46. Расчет параметров парной параболической регрессии. 47. Расчет параметров уравнения гиперболической регрессии. 48. Проверка статистической значимости параметров уравнений регрессии. 49. Линейная многофакторная регрессия. Расчет коэффициентов. Перечень тестовых заданий: Событие, которое всегда наступает в результате опыта называется… *достоверным равновозможным предпочтительным Независимым вероятным Событие, которое в результате опыта произойти не может, называется… *невозможным недостоверным случайным вероятным непредсказуемым Событие, которое в результате опыта может произойти, а может и не произойти называется… *случайным достоверным допустимым противоположным предсказуемым Вероятность события A равна P(A)=0,2, события B равна P(B)=0,35. Чему равна вероятность события C, если события A, B, C образуют полную группу событий? 0,45 Согласно статистике в некоторой местности вероятность сильного дождя в осенний день составляет 0,24, вероятность выпадения снега – 0,13, вероятность тумана – 0,34. Какова вероятность, что в этот день будут осадки? 0,37 Фирма имеет 4 контрагента в Батайске и 6 контрагентов а Аксае. На фирму прибыл контрагент для заключения договора. Какова вероятность, что он из Батайска? 0,4 Банк имеет 2 отделения, с вероятностью 0,6 независимо от других каждое отделение может заказать на завтра крупную сумму денег. Какова вероятность того, что будет хотя бы одна заявка на завтра? 0,84 В партии из 100 деталей обнаружено 6 бракованных. Найти относительную частоту появления бракованных деталей. 0,06 Два менеджера делают по одному заказу на поставку товара у разных фирм. Вероятность поставки партии товара в срок у первой фирмы составляет 0,9, у второй – 0,8. Какова вероятность того, что хотя бы одна партия товара будет поставлена в срок? 0,98 Два менеджера делают по одному заказу на поставку товара у разных фирм. Вероятность поставки партии товара в срок у первой фирмы составляет 0,9, у второй – 0,8. Какова вероятность того, что только одна партия будет поставлена в срок? 0,26 Перечень практических заданий для оценки степени владения компетенциями: № Задание 1. Задача 1 В лотерее выпущено 200 билетов, из которых i – выигрышных. Некто приобрел 4 билета. Найти вероятность того, что хотя бы один билет выиграет. Построить таблицу вероятностей для i от 1 до 20. 2.Задано распределение двумерной случайной величины: X Y 3 10 12 4 0.17 0.13 0.25 5 0.1 0.3 0.05 Найти распределение вероятностей составляющих X, Y. Найти математическое ожидание, дисперсию и моду составляющих 3. Найти М(Х), D(X), σ. Плотность распределения случайной величины Х имеет вид: 0, x 2 1 3 f ( x) ( x 6 x 2 x 8), 2 x 4 4 0, x 4. 4.ЗАДАНИЕ: Рассчитать для своего варианта Коэффициент корреляции rxy . Проверить значимость результата. X Y 88 143 92 158 97 144 89 164 99 172 116 204 77 150 98 165 83 162 7 УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ 7.1 Основная литература № п/п 1 2 3 5 6 7.2 № п/п 1 2 3 4 5 6 Перечень литературы Теория вероятностей. Учебник для экономических и гуманитарных специальностей. МЦНМО Тюрин Ю.Н., Макаров А.А., Симонова Г.И. 2009 ЭБС www.iprbookshop.ru Гмурман В. Е. Теория вероятностей и математическая статистика / В.Е. Гмурман - Москва : Высшее образование, 2009. 479 c. Гмурман В. Е. Теория вероятностей и математическая статистика : учебное пособие / В.Е. Гмурман - Москва : Высшее образование, 2009. 479 c. Кремер Н. Ш. Теория вероятностей и математическая статистика : учебник / Н.Ш. Кремер - Москва : ЮНИТИ, 2009. 543 c. Задачи по теории вероятностей. Учебное пособие. МЦНМО Ширяев А.Н.2006 ЭБС www.iprbookshop.ru Дополнительная литература Перечень литературы Тюрин Ю. Н. Анализ данных на компьютере : учебное пособие / Ю.Н. Тюрин, А.А. Макаров - Москва : ИНФРА-М, 2003. 544 c. Теория вероятностей и математическая статистика. Учебное пособие Научная книга Щербакова Ю.В. 2012 ЭБС www.iprbookshop.ru Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике : учебное пособие / В.Е. Гмурман - Москва : Высшая школа, 2001. 400 c. Теория вероятностей и математическая статистика. Учебное пособие Научная книга Щербакова Ю.В. 2012 ЭБС www.iprbookshop.ru Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике : учебное пособие / В.Е. Гмурман - Москва : Высшая школа, 2001. 400 c. Кремер Н. Ш. Теория вероятностей и математическая статистика : учебник / Н.Ш. Кремер - Москва : ЮНИТИ, 2004. 543 c. 8 ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ (УМК, КОМПЬЮТЕРНЫЕ ПРОГРАММЫ, ЭЛЕКТРОННЫЕ УЧЕБНИКИ, ИНТЕРНЕТРЕСУРСЫ) № п/п Перечень 2 Наумов О.Л. Элементы теории вероятностей. Учебно-методическое пособие. Ростов-на-Дону, ИУБиП, 2001. Excel 3 Графические калькуляторы Casio 1