Алгебра и начало анализа. Теорема Безу. 11
реклама
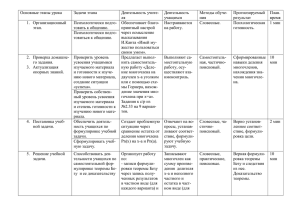
Алгебра и начало анализа. Теорема Безу. 11-й класс (физико – математический профиль) Цель: Освоить применение теоремы Безу Задачи урока: способствовать развитию готовности проведения деления многочлена на многочлен и использованию схемы Горнера; совершенствовать освоенный опыт работы в электронных таблицах OpenOffice.org Calc; организовать деятельность учащихся по восприятию, осмысливанию и первичному запоминанию новых представлений; разобрать и доказать теорему Безу при решении проблемной ситуации: можно ли разложить многочлен третьей степени на множители; рассмотреть использование теорему Безу для решения уравнений высших степеней; содействовать развитию логического мышления, внимания, речи и умения работать самостоятельно. Тип урока: урок ознакомления с новым материалом. Вид урока: урок по проблемной технологии Ход урока Технологическая карта урока Этап урока I. Организацион ный момент Время 5 минут 5 минут II. Возникновение проблемной ситуации Действия учителя Наша задача сегодня в совместной деятельности подтвердить слова Декарта Тема нашего урока «Теорема Безу» настолько значима, что даже используется в заданиях ЕГЭ и различных олимпиадах. Теорема Безу облегчает решение многих заданий, содержащих уравнения высших степеней. К сожалению, она изучается только на профильном уровне. На этом уроке мы научимся решать уравнения высших степеней, а алгоритм решения выведем сами. Решить уравнение: x3 2x2 - 6x + 4=0 . Возникает проблема: Мы понимаем, что было бы удобно представить левую часть уравнения в виде произведения, и так как Действия учащихся Читают изречение на экране «Для того, чтобы совершенствовать ум, надо больше рассуждать, чем заучивать». Декарт (1596 -1650). Французский математик, физик, филолог, философ. Для данного занятия класс разбивается на две группы по 10 человек, попеременно работающие в тетради и на компьютере. Решаем уравнение x3 - 2x2 - 6x + 4=0 10 мин. III. Актуализация опор ых знаний произведение равно нулю, то приравнять к нулю каждый множитель. Для этого надо разложить многочлен 3-ей степени на множители. Но как? Проблемный вопрос. Можно ли сгруппировать или вынести общий множитель за скобку в нашем случае? Вспомним, как разложить на множители многочлен х2 - 5х - 6? . Найдите корни трехчлена двумя способами. Какими? IV. Выдвижение 10 мин. проблемы Это значит, что трехчлен делится на каждый из дву членов: х – 6 и х + 1. Обра тите внимание на свобод ный член нашего трехчле на и найдите его делители (±1, ±2, ±3, ±6). Какие из делителей являются корня ми трехчлена? (-1 и 6) Какой вывод можно сделать? Так какой же одночлен по может подобрать корни мно гочлена? Выпишите его делители: ±1; ±2; ±4. Найдите значе ния многочлена для каждо го делителя. С помощью электронных таблиц и непо средственно: Вариант ответа: нет По формуле разложения на множи ели квадратного трехчлена: ах2 + bх + с = a(x – x1)(x-x2), где х1 и х2 корни трехчлена по формуле корней квадратного уравнения и по теореме Виета Решают на доске от каждой группы по одному ученику. Остальные учащиеся в тетрадях. Получили: х2 5х - 6 = (х - 6) (х + 1). Корни трехчлена являются делителями свободного члена Р(х) = x3 - 2x2 - 6x + 4=0? (Свобод ный член). 1 группа вычисляет в тетради Р(1)= -3 Р(-1)=7 Р(2)=-8 Р(4)=12 Р(-4)=-68 Р(-2)=0 II группа вычисляет за компьютера ми в OpenOffice.org Calc х Р(х) 1 -3 -1 7 2 -8 -2 0 4 12 -4 -68 (При вычислении в электронных таб лицах в ячейку В2 ученики вводят формулу: =А1^3-2*A1^2-6*A1+4. С Какой из делителей являет ся корнем многочлена? Как найти другие множите ли? А как еще можно? Что такое схема Горнера? . Схема Горнера x3-2x2-6x+4 2 сложить разделим на двучлен х + 1 -2 -6 4 1 -4 2 0 x3 - 2x2 - 6x + 4= (x2-4x+2)(x+ 2)= -2 помощью маркера автозаполнения получают значения многочлена во всем столбце). -2 Таким образом, один из множите лей в разложении будет х-(-2) = x+2 Разделить «в столбик» на двучлен х +2 по схеме Горнера Схема Горнера – это алгоритм деле ния многочленов, записанный для час тного случая, когда делитель равен двучлену x–a Выполняем деление: первая группа «в столбик», вторая – по схеме Горнера. остаток умножить x3 - 2x2 - 6x + 4= (x2-4x+2)(x+ 2) 1 -2 -6 4 -2 1 -4 2 0 Разделили без остатка. Вернемся к уравнению: x3 - 2x2 - 6x + 4= (x2-4x+2)(x+ 2)=0 x2-2x+2=0 - квадратное уравнение. Решите его: D1 = 4 – 2 = 2; Ответ: -2, . Значение равно нулю А мог получиться остаток при делении? Ответим на этот вопрос позднее. А сей час назовите значение мно гочлена при х = - 2. Прошу обратить ваше вни мание, что x = - 2 является корнем многочлена и оста ток от деления многочле на на х-(-2) равен 0. Рассмотрим х=1 - не явля ется корнем уравнения. Отметим, что x=1 не являя ется корнем многочлена и остаток от деления много члена на (х-1) равен значе нию многочлена при х=1. Вот и ответ на вопрос об ос Попробуем разделить многочлен на х-1. Вторая группа выполняет деление «в столбик». Первая – по схеме Горнера дополняет таблицу ещё одной строкой. 1 -2 -6 4 -2 1 -4 2 0 1 1 -1 -7 -3 3 2 Итак, x - 2x - 6x + 4 = (х – 1)∙( x2 - татке. Да, остаток получил х – 7) – 3. ся, при таком значении х, которое не является корнем многочлена. Давайте про должим схему Горнера для остальных делителей сво бодного члена. Теперь пусть первая группа вычисляет за компьютером, а вторая в тетрадях. V. Решение проблемы 5 мин. Вы заметили закономер ность об остатке. Какую? остаток получился, при таком значе нии х, которое не является корнем многочлена А давайте запишем эту зако Доказательство. Разделим Р(х) c номерность в общем виде. остатком на (x - а). Получим Р(х)= Пусть Р(х) - многочлен, а - (x - а)Q(х) + R; по определению некоторое число. Докажем остатка, многочлен r либо равен 0, утверждение: Остаток от либо имеет степень, меньшую сте пени (x - a), т.е. меньшую 1. Но сте деления Р(х) на (x - а) ра пень многочлена меньше 1 только в вен Р(а). Значения Схема случае, когда она равна 0, и поэто многочлена Горнера Р(х)=x -2x -6x+4 му в обоих случаях R на самом деле является числом – нулем или отли чным от нуля. Подставив теперь в равенство Р(х)= (x - а)Q(х) + R зна чение x = a, мы получим Р(a)= (a а)Q(х) + R, P(a) = R, так что дейст вительно R = P(a). Эту закономер ность отметил и математик Безу. Сообщение ученицы (Слайд 7) Этьенн Безу–французский математик, член Парижской Аккаде мии Наук (с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года. С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в коро левском артиллерийском корпусе. Основные работы Этьенна Безу отно сятся к высшей алгебре, они посвяще ны созданию теории решения алгеб раических уравнений. В теории ре шения систем линейных уравнений он содействовал возникновению те ории определителей, развивал тео рию исключения неизвестных из сис тем уравнений высших степеней, до казал теорему (впервые сформулиро ванную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках. Во Фран ции и за её границей вплоть до 1848 года был очень популярен его шести 3 2 1 -2 -6 4 1 -3 1 1 -1 -7 -3 -1 2 7 -8 -1 1 -3 -3 7 2 1 0 -6 -8 -2 4 0 12 -2 1 -4 2 0 4 1 2 2 12 -4 -68 -4 1 -6 18 -68 х Р(х) Гипотеза: Значение многочлена при х=а равно остатку от деления многочлена на х - а. VI. Усвоение изученного 4 мин. Решить уравне ние: х4 - x3 6x2 - x + 3 = 0. томный "Курс математики", написан ный им в 1764-69 годах. Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем урав нений, основанный на этом методе. Часть трудов Безу посвящена внеш ней баллистике. Именем ученого названа одна из основных теорем алгебры. Следствие Какой должен быть остаток, чтобы многочлен Р(х) делился нацело на двучлен (х – а)? (равен 0). Получаем следствие из теоремы Безу: Для того, чтобы многочлен Р(х) делился нацело на двучлен (х – а), необходимо и достаточно, чтобы выполнялось равенство Р(а) = 0. Целые корни многочлена Р(х) = х4 x3 - 6x2 - x + 3 должны быть делителями свободного члена, так что это могут быть числа -1, 1, 3, -3. Подберем корень по схеме Горнера: 1 -1 -6 -1 3 -1 1 -2 -4 3 0 4 3 2 х - x - 6x - x + 3= (х + 1)(х3 -2х2 – 4х +3) =0 1 -2 -4 3 -1 1 -3 -1 4 1 1 -1 -5 -2 -3 1 -5 11 -30 3 1 1 -1 0 3 Q(x) = х -2х2 – 4х +3=(x- 3)(x2 + x 1)=0; x2 + x -1 =0; D= 5, x = VII. Итог: 4 мин. Ответ: -1; 3; . Итак, что дает нам Теорема Безу? Теорема Безу дает воз можность, найдя один ко ень многочлена, искать да лее корни многочлена, сте пень которого на 1 меньше: если Р(а) = 0, то Р(х)= (x - а) Q(x), и остается решить уравне ние Q(x) = 0. Иногда этим приемом - он называ ется понижением степени – Высказывания учеников: VIII. Домашнее 2 мин задание: мож но найти все корни много члена. Вернуться к высказыванию Декарта. Удалось ли вам убедиться в справедливости слов Де карта? Как вы их поняли для себя? Решить уравнения двумя способами: а) х3 - 3х2 –х + 3 = 0; б) х4 + 4х2 – 5 = 0. Литература: Числа и многочлены: Методическая разработка для учащихся заочного отделения ММФ / Авторсоставитель А. В. Деревян кин. – М.: Издательство центра прикладных иссле дований при механико-ма тематическом факультете МГУ, 2008. «Заучивать механически бесполез но, необходимо осмысливать изуча емое», «Без размышления ум не раз вивается, потому что это будет шаб лонное мышление, которое никому неинтересно» А.Г. Мордкович, П.В. Семенов и др. и Алгебра и начала анализа. 11 класс. Учебник профильного уровня. – М.: Мнемозина, 2007; Алгебра: учеб. для учащихся 9 кл. с углубл. изучением математики / [Н. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев]; под ред. Н. Я. Виленкина. – М.: Просвещение, 2005.