4. Самостоятельная работа - Институт управления, бизнеса и
реклама
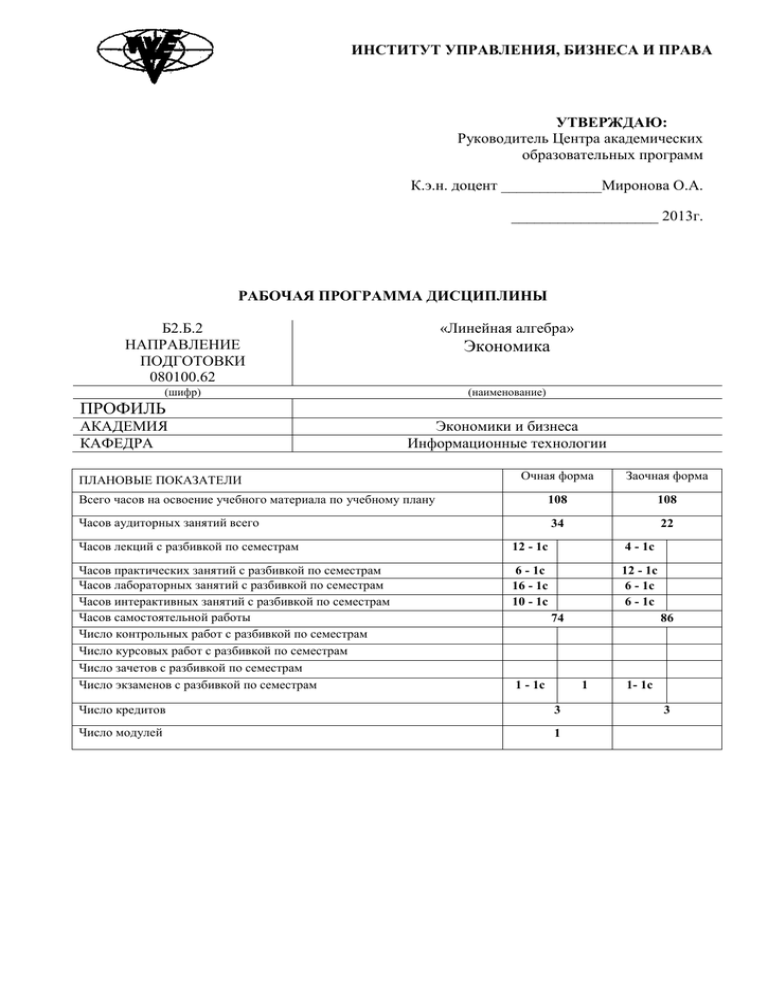
ИНСТИТУТ УПРАВЛЕНИЯ, БИЗНЕСА И ПРАВА УТВЕРЖДАЮ: Руководитель Центра академических образовательных программ К.э.н. доцент _____________Миронова О.А. ___________________ 2013г. РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ Б2.Б.2 НАПРАВЛЕНИЕ ПОДГОТОВКИ 080100.62 «Линейная алгебра» (шифр) (наименование) Экономика ПРОФИЛЬ АКАДЕМИЯ КАФЕДРА Экономики и бизнеса Информационные технологии Очная форма Заочная форма Всего часов на освоение учебного материала по учебному плану 108 108 Часов аудиторных занятий всего 34 22 ПЛАНОВЫЕ ПОКАЗАТЕЛИ Часов лекций с разбивкой по семестрам 12 - 1c 4 - 1c Часов практических занятий с разбивкой по семестрам Часов лабораторных занятий с разбивкой по семестрам Часов интерактивных занятий с разбивкой по семестрам Часов самостоятельной работы Число контрольных работ с разбивкой по семестрам Число курсовых работ с разбивкой по семестрам Число зачетов с разбивкой по семестрам Число экзаменов с разбивкой по семестрам 6 - 1c 16 - 1c 10 - 1c 12 - 1c 6 - 1c 6 - 1c 74 1 - 1c 86 1 Число кредитов 3 Число модулей 1 1- 1c 3 Автор рабочей программы Витченко О.В. (подпись) (Ф.И.О.) РАБОЧАЯ ПРОГРАММА СОСТАВЛЕНА НА ОСНОВАНИИ: 1. Федерального государственного образовательного стандарта высшего профессионального образования по направлению подготовки «Экономика» от 21.12.2009г. 2. Учебного плана направления подготовки «Экономика» от 01.07.2013 РАБОЧАЯ ПРОГРАММА ОБСУЖДАЛАСЬ И СОГЛАСОВАНА КАФЕДРОЙ: «Информационные технологии» Ткачук Е.О. (наименование) (подпись зав. каф) (Ф.И.О.) Протокол заседания кафедры № 1 от 31.08.2013 УМС Академии управления (наименование) Пивоваров И.В. (подпись председателя УМС) (Ф.И.О.) Протокол УМС № 1 от 31.08.2013 ______________ 2 1. ЦЕЛИ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ Целью преподавания дисциплины «Линейная алгебра» является изложение основных понятий и методов линейной алгебры, являющейся основой современных прикладных экономико-математических методов. Задачей изучения дисциплины «Линейная алгебра» является формирование у студентов теоретических знаний и практических навыков применения методов линейной алгебры при решении практических задач экономики. 2. ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ ДИСЦИПЛИНЫ В процессе изучения дисциплины студенты должны: Овладеть компетенциями: Перечень названий и шифров компетенций в соответствии с ФГОС ВПО Формируемые профессиональные компетенции (ПК): расчетно-экономическая деятельность способен собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов (ПК-1); способен на основе типовых методик и действующей нормативно-правовой базы рассчитать экономические и социально-экономические показатели, характеризующие деятельность хозяйствующих субъектов, (ПК-2); способен выполнять необходимые для составления экономических разделов планов расчеты, обосновывать их и представлять результаты работы в соответствии с принятыми в организации стандартами (ПК-3). Знать: основы линейной алгебры, необходимые для решения экономических задач. Уметь: применять математические методы линейной алгебры для решения экономических задач. 3 3. АУДИТОРНАЯ РАБОТА 3.1 Лекции № п/п Тема лекции 1 Алгебра матриц 2 Определители 3 Алгебра матриц (продолжение) 4 Системы линейных уравнений и основные методы их решения 5 Применение матричного исчисления к решению экономических задач Краткое содержание Матрицы. Основные определения. Действия над матрицами Определители и их свойства. Миноры и алгебраические дополнения. Вычисление определителей n-го порядка. Обратная матрица. Ранг матрицы. Линейная зависимость и независимость строк матрицы. Многочленные матрицы. Система линейных уравнений. Методы решения системы n линейных уравнений с n неизвестными. Теорема Кронекера-Карелли. Метод ЖорданаГаусса. Метод Крамера. Модели планирования производства, планирования материальных затрат, Леонтьева межотраслевого баланса. ИТОГО: Кол. часов О/З 2/2 2/- 2/- 4/- 2/2 12/4 3.2 Практические и лабораторные занятия № п/п 1 2 3 4 5 6 7 8 9 Тема занятия Действия над матрицами Вычисление определителей n-го порядка. Вычисление обратных матриц Ранг матрицы. Преобразование матриц Методы решения систем линейных уравнений Задачи с экономическим содержанием. Векторные пространства. Исследование и обсуждение модели планирования производства. Исследование и обсуждение моделей планирования материальных затрат Исследование и обсуждение модели Леонтьева межотраслевого баланса Решение задач. Практическое занятие. Решение задач. Лабораторное занятие. Кол. часов О/З 2/2 2/2 Решение задач. Практическое занятие. Решение задач. Практическое занятие. 2/2 2/2 Решение задач. Лабораторное занятие. 2/2 Решение задач. Лабораторное занятие. 2/2 Построение и исследование математической модели задачи. Лабораторное занятие. Построение и исследование математической модели задачи. Лабораторное занятие. Построение и исследование математической модели задачи. Лабораторное занятие. 2/2 Краткое содержание 4/2 4/2 ИТОГО: 22/18 4 3.3 Интерактивные занятия № п/п Тема занятия 1 Исследование и обсуждение модели планирования производства 2 Исследование и обсуждение моделей планирования материальных затрат 3 Исследование и обсуждение модели Леонтьева межотраслевого баланса Краткое содержание и вид интерактивного занятия Построение математической модели задачи, связанной с планированием производства, обеспечивающей соблюдения технологических соотношений между отдельными изделиями. Исследование модели при изменении её параметров. Работа обучаемых в подгруппах, использование информационных технологий. Лабораторное занятие. Построение математической модели задачи, связанной с планированием материальных затрат. Исследование модели при изменении её параметров. Работа обучаемых в подгруппах, использование информационных технологий. Лабораторное занятие. Построение математической модели задачи, связанной с обеспечением баланса между отраслями. Исследование модели при изменении её параметров. Работа обучаемых в подгруппах, использование информационных технологий. Лабораторное занятие. ИТОГО: Кол. часов О/З 2/2 4/2 4/2 10/6 5 4. САМОСТОЯТЕЛЬНАЯ РАБОТА № п/п Содержание самостоятельной работы Кол. часов О/З Форма контр. 1 Алгебра матриц. 10/12 Отчёт 2 Определители. 10/12 Отчёт 3 Алгебра матриц (продолжение). 10/12 Отчёт 4 Решение системы линейных уравнений 10/12 Отчёт 5 Применение матричного исчисления к решению некоторых экономических задач ИТОГО: 34/38 Отчёт 74/86 6 1. 2. 3. 4. 5. 6. 5. ТЕМЫ УЧЕБНЫХ ПРОЕКТОВ Применение матричного исчисления к решению экономических задач Массивы данных и матричные методы их обработки Обработка массивов данных средствами современных компьютерных технологий Математическая модель задачи, связанной с планированием производства, обеспечивающей соблюдения технологических соотношений между отдельными изделиями. Математическая модель задачи, связанной с планированием материальных затрат. Математическая модель задачи, связанной с обеспечением баланса между отраслями. 7 6. ТРЕБОВАНИЯ К ИТОГОВОЙ АТТЕСТАЦИИ Форма итоговой аттестации: экзамен Вопросы к экзамену. 1. Понятие матрицы. Частные виды матриц. 2. Операции над матрицами. 3. Определители квадратных матриц. 4. Свойства определителей. 5. Обратная матрица. 6. Ранг матрицы. 7. Системы mлинейных уравнений c n неизвестными: основные понятия и определения. 8. Система n линейных уравнений с n переменными. 9. Однородные системы линейных уравнений. 10. Основные методы решения системы линейных уравнений. 11. Модель Леонтьева многоотраслевой экономики. Перечень тестовых заданий. 1. Если матрица , то матрица 4A имеет вид 1) 2) 2. Если матрицы 1) 3. Для матрицы побочной диагонали. 3) 4) и 2) , то матрица 3A – 2B имеет вид 3) 4) указать сумму элементов, расположенных на 4. Для матриц выполнить указать те операции, которые можно B·A B·A BT · A A·B 5. Указать те преобразования строк (столбцов) матрицы, которые являются элементарными умножение строки (столбца) на ненулевое число 8 замена элементов строки (столбца) произвольными числами замена строки (столбца) суммой этой строки (столбца) и другой строки (столбца), предварительно умноженной на некоторое число поменять местами две строки (два столбца) замена строки (столбца) нулевой строкой (столбцом) транспонирование матрицы 6. При умножении матрицы A на матрицу B справа должно соблюдаться условие число строк матрицы A равно числу строк матрицы B число строк матрицы A равно числу столбцов матрицы B если матрицы не квадратные, то они должны быть одинакового размера верный ответ отсутствует 7. Для матриц произведения С = B A. 8. Квадратная матрица называется диагональной, если найти элемент c23 элементы, лежащие на побочной диагонали, равны нулю элементы, лежащие на главной диагонали, равны нулю элементы, не лежащие на главной диагонали, равны нулю элементы, лежащие ниже главной диагонали, равны нулю элементы, лежащие на главной диагонали, обязательно равны 9. Квадратная матрица называется верхнетреугольной, если элементы, лежащие на побочной диагонали, равны нулю элементы, лежащие на главной диагонали, равны нулю элементы, не лежащие на главной диагонали, равны нулю элементы, лежащие ниже главной диагонали, равны нулю элементы, лежащие на главной диагонали, обязательно равны 10.Установить соответствие между парой матриц A и B и их произведением A B: Матрицы A и B Произведение A · B 7 9 11.Установить соответствие между определителем и числом α, при котором этот определитель равен 0: Определитель Число α 12 -3/2 -1 -12 12. При замене некоторой строки невырожденной квадратной матрицы на сумму этой строки и какой-то другой, умноженной на число α, определитель. не изменится поменяет знак умножится на число α станет равным нулю 13. Если поменять местами две строки (два столбца) квадратной матрицы, то определитель: не изменится поменяет знак станет равным нулю увеличится в 2 раза 14. Известно, что определитель квадратной матрицы A равен Δ. Укажите, чему будет равен определитель матрицы, полученной из матрицы A умножением первой строки на число (–3). 15. Указать матрицы, которые имеют обратные 1 4 2 5 3 16. Указать верные утверждения, связанные с определением и существованием обратной матрицы: обратная матрица A-1 существует, если матрица A – квадратная и det A ≠ 0 обратная матрица A-1 существует, если матрица A – квадратная 10 обратная матрица A-1 существует, если матрица A – квадратная и вырожденная, т.е. det A ≠ 0 A·A-1 = A-1·A = E, где E – единичная матрица соответствующего размера 17. Элемент формуле: обратной матрицы A (в случае существования) вычисляется по 18. Алгебраическое дополнение A12 элемента a12 матрицы равно: . верный ответ отсутствует 19. Если матрицы равен: , то определитель матрицы A·B 0 –16 32 2 –32 20. Распределите матрицы в порядке увеличения их определителей: 1. 2. 3. 21. Разложение определителя –4a + b – 2c –a + 2b + 3c 4. 5. по второму столбцу имеет вид: верный ответ отсутствует 11 4a + b + 2c 4a – b + 2c 22. Указать, с каким знаком («плюс» или «минус») произведение a12a23a31 входит в определитель третьего порядка . 23. Если матрица системы n уравнений квадратная и ее определитель не равен нулю, то система не имеет решений имеет единственное решение имеет не более n решений имеет ровно n решений имеет бесконечно много решений 24. При решении системы по правилу Крамера используют формулы 25. Если , то 26. Найти значение b, при котором система совместна 27. Найти значение а, при котором система несовместна 28. При решении системы по правилу Крамера верно 12 29. Пусть дана система Тогда ее решение через обратную матрицу находится как 4 30. В системе базисными можно объявить переменные 1) 2) 3) 4) 5) 6) 31. Модель Леонтьева - это а) модель межотраслевого баланса; б) модель планирования производства; 13 в) уравнение равновесия рынка. 32. Модель Леонтьева с матрицей А называется продуктивной, если а) матрица А позволяет произвести любой неотрицательный вектор потребления; б) элементы матрицы А неотрицательны; в) коэффициенты прямых затрат меньше единицы; г) коэффициенты прямых затрат положительны; 33. В модели Леонтьева с матрицей А=(aij) числа aij называются а) конечными продуктами; б) коэффициентами прямых затрат; в) элементами вектора потребления; 34. Задан межотраслевой баланс открытой двухсекторной экономики. Сельское хозяйство промышленность Домашние хозяйства Сельское хозяйство 20 30 150 Промышленность 30 40 30 Вектор выпуска продукции равен вектору 200 120 50 150 а) ; □ б) ; □ в) ; □ г) . 100 290 70 30 39 Задан межотраслевой баланс открытой двухсекторной экономики. Сельское хозяйство промышленность Домашние хозяйства Сельское хозяйство 20 30 150 Промышленность 30 40 30 Вектор потребления продукции равен вектору 200 120 50 150 а) ; б) в) г) . ; ; 100 290 70 30 40. Модель Леонтьева с матрицей А и вектором потребления C называется продуктивной, если а) уравнение АX–X=C имеет неотрицательное решение для любого C ≥ 0; б) элементы матрицы А неотрицательны; в) коэффициенты прямых затрат меньше единицы; г) уравнение АX–X=C имеет решение. 41. При решении задачи на определение количества продукции выпускаемой по плану каждым из 4-х предприятий, входящих в объединение, получено следующее матричное уравнение: 1) 8%; 2) 12% 3) 26% 4) 27% 42. В таблице приведены данные по балансу между двумя отраслями за некоторый период. Найти коэффициент a11 модели Леонтьева (Вес: 1) 14 43. Для модели Леонтьева многоотраслевой экономики вида X=AX+Y в таблице приведены частичные данные по балансу между двумя отраслями за некоторый период. Найти количество конечного продукта первой отрасли (Вес: 1) 44. Для модели Леонтьева многоотраслевой экономики вида X=AX+Y в таблице приведены данные по балансу между двумя отраслями за некоторый период. Найти количество валового продукта второй отрасли, если конечный продукт первой отрасли будет увеличен в два раза Перечень практических заданий для оценки степени владения компетенциями: 1. Модель планирования производства Имеется определенное количество изделий (деталей, полуфабрикатов, узлов), которые необходимы для производства других изделий, в том числе конечной продукции. Между отдельными изделиями должны соблюдаться технологические соотношения. Например: Детали Узлы Изделия Рис. 1. 15 Стрелки и числа на них показывают, сколько единиц i-го изделия необходимо для изготовления единицы j-го изделия. В общем виде эта информация может быть представлена в виде матрицы затрат: A (aij ) n,n . Если, кроме того, требуется определенное количество деталей и узлов в качестве запасных частей, то для построения математической модели целесообразно также ввести X ( x1 , x2 ,..., xn )T - общий выпуск, Y ( y1 , y2 ,..., yn )T - конечный выпуск. Тогда x1 y1 a11 x1 a12 x2 ... a1n xn x2 y2 a21 x1 a22 x2 ... a2 n xn ....................................................... xn yn an1 x1 an 2 x2 ... ann xn X Y A X Если задан конечный выпуск, а требуется найти общий выпуск, то задача состоит в том, чтобы разрешить эту систему относительно Х: X A X Y E X A X Y ( E A) X Y X ( E A) 1 Y Решение задачи допускается с применением среды MS Excel. 2. Модель планирования материальных затрат 1. Расчет общих затрат материалов Для того чтобы заготовить нужное количество сырья и материалов, необходимо прежде всего рассчитать общие материальные затраты на предприятии. Обозначим через bkj – затраты материалов k-го вида на производство одного n изделия j-го вида (k 1, m; j 1, n) , а через bk bkj X j - общие затраты j 1 материалов k-го вида. Если объединить все bk в вектор b (b1 , b2 ,...,bm )T , а все bkj в матрицу B (bkj ) m, n , то имеет место равенство b B x , где B – матрица материальных затрат, b - вектор суммарных материальных затрат. Подставив Х из (8.1.1) получим формулу для вектора суммарных материальных затрат b B ( E A) 1 Y 16 2. Расчет суммарной стоимости затраченных материалов. Если заданы цены всех материалов Pk (k 1, m) , то суммарная стоимость всех затраченных материалов вычисляется по формуле: K P T b P T B ( E A) 1 Y где P T ( P1 , P2 ,..., Pm ) . 3. Расчет стоимости затрат по каждому виду материалов. Если требуется определить стоимость затрат по каждому виду материалов, то целесообразно использовать не вектор, а диагональную матрицу цен, т.е. P1 0 ... 0 0 P2 ... 0 . P ... ... ... ... 0 0 ... P m Вектор K стоимости затрат по каждому виду материалов получается следующим образом: K P b P B ( E A) 1 Y Решение задачи допускается с применением среды MS Excel. 17 7. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ 7.1 Основная литература № п/п 1 Перечень литературы Кремер Н. Ш. Высшая математика для экономистов: учебник для вузов / Н.Ш. Кремер – Москва : ЮНИТИ, 2010. 483 c. Кремер Н. Ш. Высшая математика для экономического бакалавриата. Учебник и практикум / Н.Ш. Кремер – Москва: Юрайт-издат, 2012.- 223 c. 7.2 Дополнительная литература 2 № п/п Перечень литературы 1 1.Виленкин И.В. Высшая математика для студентов экономических, технических, естественно-научных специальностей вузов: пособие / И.В. Виленкин, В.М. Гробер – Ростов-на-Дону: Феникс, 2008. 414 c. 2 Воронов М.В. Высшая математика для экономистов и менеджеров: учебное пособие / М.В. Воронов, Г.П. Мещеряков – Ростов-на-Дону: Феникс, 2004. 288 c. Красс М. С. Математика для экономистов: учебное пособие / М.С. Красс, Б.П. Чупрынов – Санкт-Петербург: Питер, 2009. 464 c. Соболь Б.В. Практикум по высшей математики: учебная книга / Б.В. Соболь, Н.Т. Мишняков, В.М. Поркшеян – Ростов-на-Дону: Феникс, 2007. 630 c. Макаров С.И. Математика для экономистов: учебное пособие / С.И. Макаров – Москва: КноРус, 2007. 264 c. Самаров К.Л. Финансовая математика: практический курс: учебное пособие / К.Л. Самаров – Москва : Альфа-м, 2005. 80 c. Малугин В.А. Математика для экономистов: Линейная алгебра. Курс лекций. – М.: Эксимо, 2006. – 224 с. (серия Высшее экономическое образование) 3 4 5 6 7 18 8. ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ (УМК, КОМПЬЮТЕРНЫЕ ПРОГРАММЫ. ЭЛЕКТРОННЫЕ УЧЕБНИКИ, ИНТЕРНЕТ-РЕСУРСЫ) № п/п Перечень Романников А.Н. Линейная алгебра // Московский государственный университет экономики, статистики и информатики. – М., 2010. – 180 с. (файл «УП_Линейная алгебра.doc») 2. WWW.EXPONENTA.RU 1. Малугин В.А. Математика для экономистов: Линейная алгебра. Курс лекций. М.: Эксмо, 2010. – 224 с. (Высшее экономическое образование). Файл «160- Математика для экономистов_Линейная алгебра_Малугин_2006» 4. Математические web-сервисы. http://www.mathelp.spb.ru/solver.htm 3. 5. Российское образование. Федеральный портал. (www.edu.ru) Математическое Бюро: Решение задач по высшей математике (www.matburo.ru) Нехудожественная библиотека (www.nehudlit.ru) 19 ЛИСТ ИЗМЕНЕНИЙ 2-й учебный год (____/_____) действия рабочей программы Автор рабочей программы ______________________________________»__»________20__ Зав кафедрой »__»________20___ 3-й учебный год (____/_____) действия рабочей программы Автор рабочей программы ______________________________________»__»________20__ Зав кафедрой »__»________20___ 4-й учебный год (______/______) действия рабочей программы Автор рабочей программы ______________________________________»__»________20__ Зав кафедрой »__»________20___ 5-й учебный год (______/______) действия рабочей программы Автор рабочей программы ______________________________________»__»________20__ Зав кафедрой »__»________20___ 20
