Алгебра 10
реклама
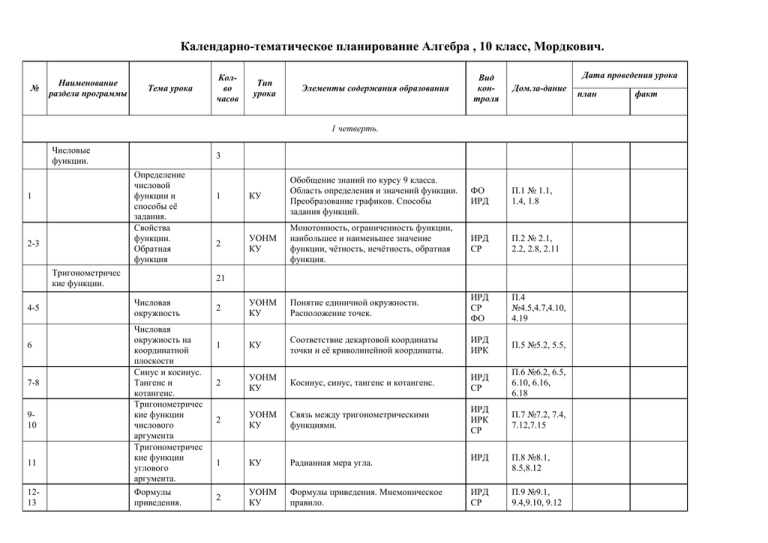
Календарно-тематическое планирование Алгебра , 10 класс, Мордкович. № Наименование раздела программы Тема урока Колво часов Тип урока Элементы содержания образования Вид контроля Дата проведения урока Дом.за-дание 1 четверть. Числовые функции. 3 Определение числовой функции и способы её задания. Свойства функции. Обратная функция 1 2-3 Тригонометричес кие функции. 4-5 6 7-8 910 11 1213 1 КУ Обобщение знаний по курсу 9 класса. Область определения и значений функции. Преобразование графиков. Способы задания функций. 2 УОНМ КУ Монотонность, ограниченность функции, наибольшее и наименьшее значение функции, чётность, нечётность, обратная функция. ИРД СР П.2 № 2.1, 2.2, 2.8, 2.11 2 УОНМ КУ Понятие единичной окружности. Расположение точек. ИРД СР ФО П.4 №4.5,4.7,4.10, 4.19 1 КУ Соответствие декартовой координаты точки и её криволинейной координаты. ИРД ИРК П.5 №5.2, 5.5, 2 УОНМ КУ Косинус, синус, тангенс и котангенс. ИРД СР П.6 №6.2, 6.5, 6.10, 6.16, 6.18 2 УОНМ КУ Связь между тригонометрическими функциями. ИРД ИРК СР П.7 №7.2, 7.4, 7.12,7.15 1 КУ Радианная мера угла. 2 УОНМ КУ Формулы приведения. Мнемоническое правило. ФО ИРД П.1 № 1.1, 1.4, 1.8 21 Числовая окружность Числовая окружность на координатной плоскости Синус и косинус. Тангенс и котангенс. Тригонометричес кие функции числового аргумента Тригонометричес кие функции углового аргумента. Формулы приведения. ИРД П.8 №8.1, 8.5,8.12 ИРД СР П.9 №9.1, 9.4,9.10, 9.12 план факт № 14 Наименование раздела программы Контрольная работа № 1 «Тригонометрические функции» Функции у=sin x, у=Cos x, их свойства и графики. 1517 18 Тема урока Резерв. Колво часов Тип урока 1 3 УОНМ КУ Элементы содержания образования Вид контроля Дата проведения урока Дом.за-дание Уметь применять полученные знания по теме в комплексе. КР Свойства функций. Построение графика функций. ИРД ИРК СР П.10,11 №10.1,10.4, 10.11,11.2,11. 4,11.8 1 2 четверть. 19 2021 2223 24 Периодичность функций Y=sin x y=cos x. Преобразование графиков тригонометрическ их функций. Функции Y=tg x y=ctg x, их свойства и графики. Контрольная работа № 2 «Тригонометрические функции, их свойства и графики» Тригонометричес кие уравнения. 2526 2728 29 1 КУ Период функции. Периодичность функций. ИРД П.12 №12.1, 12.3,12.5 2 УОНМ КУ Преобразование графиков. ИРД СР П.13 №13.2, 13.4,13.11,13. 16 2 УОНМ КУ Свойства графиков функций. Тангенсоида. ИРД СР П.14 №14.2, 14.4, 14.6, 14.10 Уметь применять полученные знания по теме в комплексе. КР 1 11 Арккосинус. Решение уравнения cos t=а. Арксинус. Решение уравнения sin t=а. Арктангенс и арккотангенс. Решение уравнений tg x =а, ctg x=а. 2 УОНМ КУ Понятие арккосинуса. ИРД СР 2 УОНМ КУ Понятие арксинуса. ИРД СР 1 КУ Понятие арктангенса и арккотангенса. ИРД П.15 №15.1, 15.4, 15.7,15.17 П.16 №16.2, 16.5, 16.7,16.10 П.17 №17.2, 17.5, 17.7 план факт № Наименование раздела программы Тригонометричес кие уравнения. 3031 32 Тема урока Резерв Колво часов 2 Тип урока УОНМ КУ Элементы содержания образования Простейшие тригонометрические уравнения. Методы решения уравнений. Вид контроля Дата проведения урока Дом.за-дание ИРК СР П.18 №18.2, 18.5,18.8, 18.10,18.16 Простейшие тригонометрические уравнения. Методы решения уравнений. ИРК СР п.18 №18.9, 18.18 Уметь применять полученные знания по теме в комплексе. КР 1 3 четверть. Тригонометричес кие уравнения. 3334 35 3637 38 3941 42 2 Контрольная работа № 3 «Решение тригонометрических уравнений» 1 Преобразование тригонометрическ их уравнений. 7 Синус и косинус суммы и разности аргументов. Тангенс суммы и разности аргументов. Формулы двойного аргумента. Преобразование сумм тригонометрическ их функций Контрольная работа № 4 «Преобразование тригонометрических выражений» УЗИМ КУ 2 УОНМ КУ Синус и косинус суммы и разности аргументов. ИРД СР 1 КУ Тангенс суммы и разности аргументов. ИРК Формулы двойного аргумента. Прочие преобразования тригонометрических выражений. ИРД ИРК СР 3 1 УОНМ КУ УЗИМ КР П.19 №19.2, 19.4, 19.6, 19.9, 19.21 П.20 №20.2,20.6, 20.14 П.21 №21.2, 21.4, 21.7,, 21.13,21.23,21 .35 план факт № Наименование раздела программы Тема урока Производная Колво часов Тип урока Элементы содержания образования Вид контроля Дата проведения урока Дом.за-дание 26 4344 Числовые последовательнос ти, их свойства, предел последовательнос ти. 2 УОНМ КУ 4546 Предел функции. 2 УОНМ КУ 4748 Определение производной. 2 УОНМ КУ 4950 Вычисление производной. 2 УОНМ КУ 51 Контрольная работа № 5 «Предел функции. Вычисление производной» 1 52 Резерв. 1 Числовые последовательности и способы их задания. Ограниченная последовательность. Возрастающая и убывающая последовательности. Предел последовательности. Свойства сходящихся последовательностей. Предел функции на бесконечности. Утверждения необходимые для вычисления предела на бесконечности. Предел функции в точке. Приращение аргумента, приращение функции. Понятие производной. Определение производной. Алгоритм нахождения производной. ИРД СР п. 24 №24.2 24.5, 24.9, 24.18 ИРД СР П.26 №26.2, 26.6, 26.7, 26.14 ИРК СР Формулы дифференцирования. Правила дифференцирования. ИРД СР Уметь применять полученные знания по теме в комплексе. КР П.27 №27.2, 27.4, 27.6, 27.10 П.28 № 28.2, 28 4, 28.6, 28.9 4 четверть. 5354 5557 5859 Уравнение касательной к графику функции. Применение производной для исследования функций на монотонность и экстремумы. Построение графиков функций. 2 3 2 УОНМ КУ Алгоритм составления уравнения касательной. ИРД СР П.29 №29.2, 29.4, 29.6, 29.13 УОНМ КУ УЗИМ Исследование функции на монотонность, нахождение точек экстремума функции. ИРД ИРК СР П.30 №30.2, 30.4, 30.7, 30.9, 30.18, 30.23 Построение графиков функций. ИРД СР П.31 № 31.1, 31.5, 31.7 УОНМ КУ план факт № Наименование раздела программы Тема урока 60 Контрольная работа № 6 «Применение производной для исследования функций» Применение производной для 61отыскания 62 наибольшего и наименьшего значений . Задачи на отыскание 63наибольших и 65 наименьших значений величин. Колво часов Тип урока 1 Элементы содержания образования Вид контроля Уметь применять полученные знания по теме в комплексе. КР Дата проведения урока Дом.за-дание 2 УОНМ КУ Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции на отрезке. ИРД ИРК СР П.32 №32.2, 32.4, 32.7, 32.15 3 УОНМ КУ УЗИМ Этапы решения задач на оптимизацию. ИРД ИРК СР № 32.21, 32.24, 32.28, 32.35 Уметь применять полученные знания по теме в комплексе. КР 66 Контрольная работа № 7 «Применение производной для решения задач» 1 6768 Резерв. 2 план факт Календарно-тематическое планирование Алгебра , 11 класс № Наименование раздела программы Тема урока Колво часов Тип урока Элементы содержания образования Вид контроля Дата проведения урока Дом.за-дание 1 четверть. Степени и корни. Степенные функции. 12 1- Понятие корня п-ой степени из действительного числа. 1 2-3 Функции у= n x , их свойста и графики. 2 УОНМ КУ Свойства функции, график, симметричность относительно прямой у=х. 4-5 Свойства корня пой степени. 2 УОНМ КУ Теоремы о корне из произведения и частного двух неотрицательных чисел, о возведении в степень, извлечения корня из корня. 6-7 Преобразование выражений, содержащих радикалы. 2 КУ УЗИМ Все свойства корня п-ой степени. УОНМ Контрольная работа № 1 «Функция 8 9-10 у= n x , преобразование выражений, содержащих радикалы». Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. 1112 Показательная и логарифмическая функции. 1314 Корень п-ой степени из неотрицательного числа, корень нечётной степени из отрицательного числа. ИРД ИРК ИРД ИРК СР ИРД ИРК СР ИРД ИРК СР п.33 № 33.3, 33.7,33.15 п. 34 № 34.5, 34.9, 34.17, 34.21 п.35 № 35.3, 35.9, 35.12, 35.17, 35.27 п.36 № 36.3, 36.7, 36.11, 36.14, 36.23, подготовка к КР Уметь применять полученные знания по теме в комплексе. 1 2 УОНМ КУ Понятие о дробном показателе степени, свойства дробно-рациональных степеней. ИРД ИРК СР 2 УОНМ КУ Определение степенной функции с рациональным показателем, графики степенной функции в зависимости от степени. ИРД ИРК СР УОНМ КУ Отличие показательной и степенной функций, определение степенной функции, асимптоты графика. ИРД ИРК СР п.37 № 37.4, 37.8, 37.13, 37.19, 37.32 п.38 № 38.5, 38.10, 38.14, 38.18, 38.23, 38.32, 38.36 23 Показательная функция, её свойства и график. 2 п.39 № 39.5, 39.11, 39.18, 39.23, 39.29 план факт № Наименование раздела программы Колво часов Тема урока Показательные уравнения и неравенства. 1516 3 17 Контрольная работа № 2 « Степенная и показательная функции» 1 18 Резерв. 1 Тип урока УОНМ КУ УЗИМ Элементы содержания образования Определение показательного уравнения и неравенства, три метода решения уравнений: функционально-графический, метод уравнивания показателей, введения новой переменной. Вид контроля ИРД ИРК СР Дата проведения урока Дом.за-дание п.40 № 40.4, 40.10, 40.15, 40.23, 40.28, 40.31, 40.34, 40.38, 40.44 Уметь применять полученные знания по теме в комплексе. 2 четверть. 19 2021 Понятие логарифма. Функция у =log Понятие логарифма, свойства логарифма. 1 a x, её свойства и график. 2 УОНМ КУ Свойства функции у =log a x, её график при а>1 , а < 1. ИРД ИРК ИРД ИРК СР 2223 Свойства логарифмов. 2 УОНМ КУ Свойства логарифма произведения, частного и другие свойства. ИРД ИРК СР 2426 Логарифмические уравнения. 3 УОНМ КУ УЗИМ Определение логарифмического уравнения, способы решений. ИРД ИРК СР 27 Контрольная работа № 3 «Логарифмическая функция, логарифмические уравнения» 2829 Логарифмические неравенства. 3031 Переход к новому основанию логарифма. п.41 № 41.4, 41.9, 41.14 п.42 № 42.4, 42.8, 42.12, 42.15, 42.18, 42.22, 42.25 п.43 № 43.5, 43.9, 43.13, 43.19, 43.23, 43.27 п.44 № 44.3, 44.8, 44.10, 44.15, 44.19, 44.21 Уметь применять полученные знания по теме в комплексе. 1 2 УОНМ КУ Понятие логарифмического неравенства при а больших или при а меньших 1, область определения логарифма. ИРД ИРК СР п. 45 № 45.5,45.8, 45.11, 45.13, 45.16, 45.18 2 УОНМ КУ Формула перехода к новому основанию. ИРД ИРК СР п.46 № 46.4, 46.9, 46.13 план факт № 32 Наименование раздела программы Тема урока Резерв. Колво часов Тип урока Элементы содержания образования Вид контроля Дата проведения урока Дом.за-дание 1 3 четверть. 3334 35 Дифференцировани е показательной и логарифмической функций. Контрольная работа № 4 « Логарифмические неравенства. Дифференцирование функций». Первообразная и интеграл. Первообразная. 3941 Определённый интеграл. 4344 x Число е. Функция у = е , её свойства, график, дифференцирование. Натуральные логарифмы, дифференцирование. ИРД ИРК СР п.47 № 47.4, 47.9, 47.13, 47.16, 47.21, 47.25 Уметь применять полученные знания по теме в комплексе. 1 7 3638 42 2 УОНМ КУ 3 УОНМ КУ УЗИМ Определение первообразной, правила первообразных, свойства первообрзных. ИРД ИРК СР 3 УОНМ КУ УЗИМ Задачи, приводящие к понятию определённого интеграла. Формула Ньютона-Лейбница. Вычисление площадей плоских фигур с помощью интеграла. ИРД ИРК СР Контрольная работа № 5 «Первообразная и интеграл». 1 Элементы математической статистики, комбинаторики и теории вероятностей. 7 Статистическая обработка данных, вероятностные задачи. 2 п.48 № 48.3, 48.7, 48.12, 48.17, 48.19, 48.22 п.49 № 49.3, 49.6, 49.10, 49.15, 49.20, 49.25, 49.31 Уметь применять полученные знания по теме в комплексе. УОНМ КУ Повторение материала 9 класса. Многоугольник распределения, гистограмма распределения, основные этапы статистической обработки данных, объём, мода, размах, среднее, варианта, частота, дисперсия, вероятность случайного события. ИРД ИРК СР п.50 № 50.3, 50.6, 50.9, 50.11, 51.3, 51.7, 51.12 план факт № Наименование раздела программы Тема урока Колво часов Тип урока ИРД ИРК СР ИРД ИРК Дата проведения урока Дом.за-дание п.52 № 52.3, 52.6, 52.11, 52.14, 52.17 4546 Сочетания и размещения. 2 47 Формула бинома Ньютона. 1 Формула бинома Ньютона. 2 УОНМ КУ Использование комбинаторики для подсчёта вероятностей, произведение событий, вероятность суммы двух событий, независимость событий, теорема Бернулли, геометрическая вероятность. ИРД ИРК СР п. 54 № 54.2, 54.5, 54.8, 54.12, 54.17, 54.24 УОНМ КУ Определение равносильности, теоремы о равносильности уравнений., область определения, ОДЗ, преобразование данного уравнения в уравнение- следствие, о проверке корней, о потере корней. ИРД ИРК СР п.55 № 55.4, 55.7, 55.8, 55.9, 55.11 Случайные события и их вероятности. 4849 Уравнения и неравенства. Системы уравнений и неравенств. 52 Сочетания и размещения, факториалы. п.53 № 53.2, 53.6 17 Равносильность уравнений 5051 УОНМ КУ Элементы содержания образования Вид контроля Резерв. 2 1 4 четверть. 5354 Общие методы решения уравнений. 2 УОНМ КУ Замена, разложение на множители, введение новой переменной, функциональнографический метод. 5557 Решение неравенств с одной переменной. 3 УОНМ КУ УЗИМ Равносильность неравенств, системы и совокупности неравенств, иррациональные неравенства, неравенства с модулями. 58 Уравнения и неравенства с двумя переменными. 1 УЗИМ Понятие уравнения и неравенства с двумя переменными. ИРД ИРК СР ИРД ИРК СР ИРД ИРК п.56 № 56.4, 56.6, 56.9, 56.13,56.20, 56.25, 56.30, 56.35 п.57 № 57.3, 57.7, 57.10, 57.17, 57.23, 57.27, 57.30 п.58 № 58.2, 58.5, 58.8, 58.11, 58.14, 58.20 план факт № Наименование раздела программы Тема урока Колво часов Вид контроля Тип урока Элементы содержания образования Решение системы, равносильные системы, этапы работы. ИРД ИРК СР Уравнение с параметром а, рассмотрение нескольких случаев. ИРД ИРК СР 5961 Системы уравнений. 3 УОНМ КУ УЗИМ 6264 Уравнения и неравенства с параметрами. 3 УОНМ КУ УЗИМ 65 Контрольная работа № 6 « Решение уравнений и неравенств. 1 6667 Итоговое повторение 2 68 Резерв. 1 Дата проведения урока Дом.за-дание п.59, № 59.3, 59.5, 59.9, 59.13, 59.18, 59.21, п. 60 № 60.2, 60.5, 60.9, 60.11,60.14 Уметь применять полученные знания по теме в комплексе. КУ УЗИМ ИРД ИРК СР Задания по тестам. план факт Требования к уровню подготовки учащихся 10 -11 классов. В результате изучения алгебры на базовом уровне ученик должен Знать/понимать значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе; значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии; универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер различных процессов окружающего мира; Уметь выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: практических расчетов по формулам, включая формулы, содержащие степени и тригонометрические функции; определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику и в простейших случаях по формуле поведение и свойства функций; находить по графику функции наибольшие и наименьшие значения; решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: описания с помощью функций различных зависимостей, представления их графически, интерпретация графиков; вычислять производные элементарных функций, используя справочные материалы; исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: решения прикладных задач, в том числе социально – экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения; составлять уравнения и неравенства по условию задачи; использовать для приближенного решения уравнений и неравенств графический метод; изображать на плоскости множества решений простейших уравнений и их систем; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: построения и исследования простейших математических моделей; решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул; вычислять в простейших случаях вероятности событий на основе подсчета числа исходов; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: анализа реальных числовых данных, представленных в виде диаграмм, графиков; анализа информации статистического характера; Пояснительная записка Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования. Данная рабочая программа ориентирована на учащихся 10-11 классов и реализуется на основе следующих документов: 1. Программа для общеобразовательных школ, гимназий, лицеев: Сборник “Программы для общеобразовательных школ, гимназий, лицеев: Математика. 5-11 кл.”/ Сост. Г.М.Кузнецова, Н.Г. Миндюк. – 3-е изд., стереотип.- М. Дрофа, 2002; 4-е изд. – 2004г. 2. Стандарт основного общего образования по математике. Стандарт среднего (полного) общего образования по математике // Математика в школе.– 2004г,№ 4 ,- с.9 Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. Рабочая программа выполняет две основные функции: Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета. Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся. Место предмета в федеральном базисном учебном плане Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени среднего (полного) общего образования отводится 4 ч в неделю 10 и 11 классах. Из них на алгебру и начала анализа по 2 часа в неделю или 68 часов в 10 классе и 68 часов в 11 классе.. Примерная программа рассчитана на 270 учебных часов (на алгебру и геометрию). В настоящей рабочей программе изменено соотношение часов на изучение тем, исключены темы элементов статистики, так как данные темы рассматриваются в 7-9 классах. (подробнее расписано в Содержании тем учебного курса). Общая характеристика учебного предмета При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи: систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач; расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей; развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления. СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА 10 КЛАССА. Глава 1. Числовые функции. (3) Повторение материала 9 класса о функциях. Область определения, область значений, функция, аргумент, понятие графика функции, преобразование графиков функций.Свойства функций. Кроме изученных в 9 классе вводится понятие монотонности, ограниченности. Понятие наибольшего и наименьшего значений. Непрерывность функций, чётность и нечётность. Обратная функция и её график. Глава. 2. Тригонометрические функции. (21). Знакомство с моделями «числовая окружность» и «числовая окружность на координатной плоскости». Синус, косинус как координаты точки числовой окружности, тангенс и котангенс. Тригонометрические функции числового аргумента и связи между ними. Тригонометрические функции углового аргумента, радианная мера угла. Функции y=sin x, y═cos x, их свойства и графики. Формулы приведения. Периодичность функций y=sin x, y═cos x. Сжатие и растяжение графика функций, график гармонического колебания. Функции y=tg x, y═ctg x, их свойства и графики. Параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y ═ x. Глава. 3. Тригонометрические уравнения. (11). Первое представление о решении тригонометрических уравнений и неравенств. Арккосинус и решение уравнения cos x ═ а, арксинус и решение уравнения sin x ═ а, арктангенс и решение уравнения tg x ═ а, арккотангенс и решение уравнения сtg x ═ а. Решение тригонометрических уравнений методом введения новой переменной; однородные тригонометрические уравнения. Глава. 4. Преобразование тригонометрических выражений. (7). Синус и косинус суммы и разности аргументов. Тангенс суммы разности аргументов. Формулы двойного аргумента, формулы понижения степени. Формулы половинного угла. Преобразования сумм тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование выражения А sin x + В cos x к виду С sin (x + t). Преобразования простейших тригонометрических выражений. Глава. 5. Производная . (26). Числовые последовательности (определение, параметры, свойства). Понятие предела последовательности (на наглядно-интуитивном уровне). Существование предела монотонной ограниченной последовательности (простейшие случаи вычисления пределов последовательности: длина окружности и площадь круга как пределы последовательностей; вычисление суммы бесконечной геометрической прогрессии). Предел функции на бесконечности и в точке. Понятие о непрерывности функции. Приращение аргумента, приращение функции. Определение производной: задачи, приводящие к понятию производной, определение производной, ее геометрический и физический смысл, алгоритм отыскания производной. Вычисление производных: формулы дифференцирования для функций у = С, у = kx+m, y = x, y = 1/x, y =√x, y = sin x, y = cos x), правила дифференцирования (суммы, произведения, частного), дифференцирование функций y = x ³, y = tg x, y = ctg x, y = xª , дифференцирование функции y = f (kx + m). Уравнение касательной к графику функции. Производные обратной функции и композиции данной функции с линейной. Примечание производной для исследования функций: исследование функций на монотонность, отыскание точек экстремума, построение графиков функций. Отыскание наибольших и наименьших значений непрерывной функции на промежутке, задачи на отыскание наибольших и наименьших значений величин. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА 11 КЛАССА. Глава 6. Степени и корни. Степенные функции.(12) Понятие корня п-й степени из действительного числа. Функции у= n x , их свойства и графики. Свойства корня н-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Глава 7. Показательная и логарифмическая функции.(23) Показательная функция, её свойства и график. Показательные уравнения. Показательные неравенства. Понятие логарифма. Функция у=log x , её свойства и график. Свойства логарифма. Логарифмические уравнения. Логарифмические неравенства. Переход к новому основанию логарифма. Дифференцирование показательной и логарифмической функций. Глава 8. Первообразная и интеграл.(7) Первообразная. Правила отыскания первообразных. Неопределённый интеграл. Таблица основных неопределённых интегралов. Задачи, приводящие к понятию определённого интеграла. Понятие определённого интеграла. Формула Ньютона-Лейбница. Вычисление площадей плоских фигур с помощью определённого интеграла. Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей.(7) Статистическая обработка данных. Простейшие вероятностные задачи. Сочетания и размещения. Формула бинома Ньютона. Случайные события и их вероятности. Глава 10. Уравнения и неравенства. Системы уравнений и неравенств.(17) Равносильность уравнений. Общие методы решения уравнений: замена уравнения, разложение на множители, введение новой переменной, функционально-графический метод. Решение неравенств с одной переменной. Равносильность неравенств, системы и совокупности неравенств, иррациональные неравенства, неравенства с модулями. Системы уравнений. Уравнения и неравенства с параметрами. Итоговое повторение.(3) Учебно-методическое и информационное обеспечение курса Основная литература: Учебник: А. Г. Мордкович Алгебра и начала математического анализа 10–11 классы в двух частях ( базовый уровень) - М.: Мнемозина 2009 г.; Самостоятельные работы: Л.А. Александрова; под редакцией А.Г. Мордковича – М. : Мнемозина, 2008 Дополнительная литература: 1. Настольная книга учителя математики М.: ООО «Издательство АСТ»: ООО «Издательство Астрель» 2004 г.; 2. Тематическое приложение к вестнику образования № 4 2005 г.; 3. Программа для общеобразовательных школ, гимназий, лицеев. Математика 5–11 кл. М.: Дрофа 2001 г.; 4. А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчиская Алгебра и начала анализа 10–11 классы. Задачник – М: Мнемозина 2003, 2004 г.; 5. А. Г. Мордкович Алгебра и начала анализа 10–11 классы. Пособие для учителей М.: Мнемозина 2004 г.; 6. А. Г. Мордкович, Е. Е. Тульчиская Алгебра и начала анализа 10–11 классы. Контрольные работы - М.: Мнемозина 2005 г.; 7. А. Г. Мордкович, П.В.Семенов Алгебра и начала анализа 10-11класс. Учебник для профильного уровня - М.: Мнемозина 2005 г.; 8. Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. Учреждений/ С.М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. - М.: Просвещение, 2003. Приложения к рабочей программе алгебра 10 класс: Самостоятельные работы С1. Определение числовой функции и способы её задания. С2. Свойства функций. С3. Обратные функции. С4,5. Числовая окружность. С6. Числовая окружность на координатной плоскости. С7,8. Синус, косинус, тангенс и котангенс. С9. Тригонометрические функции числового аргумента. С10. тригонометрические функции углового аргумента. С11. Формулы приведения. С12. Функция синус, её свойства и график. С13. Функция косинус, её свойства и график. С14. Периодичность функций. С15,16 Преобразования тригонометрических функций. С17. Функции тангенс и котангенс, их свойства и графики. С18. Арккосинус и решение уравнения cos t=а. С19. Арксинус. Решение уравнения sin t=а. С20. Арктангенс и арккотангенс. Решение уравнений tg x =а, ctg x=а. С21-23 Тригонометрические уравнения. С25,26 Синус и косинус суммы и разности аргументов. С27. Тангенс суммы и разности аргументов. С28,29. Формулы двойного аргумента. С30,31. Преобразование тригонометрических выражений. С33. Предел последовательности. С35. Предел функции. С36. Определение производной С37-40. Вычисление производной. С41,42. Уравнение касательной к графику функции. С43,44. Применение производной для исследования функций на монотонность и экстремумы. С45. Построение графиков функций. С46. Применение производной для отыскания наибольшего и наименьшего значений. С47 Задачи на отыскание наибольших и наименьших значений величин. Контрольные работы Контрольная работа № 1 «Тригонометрические функции» Контрольная работа № 2 «Тригонометрические функции, их свойства и графики» Контрольная работа № 3 «Решение тригонометрических уравнений» Контрольная работа № 4 «Преобразование тригонометрических выражений» Контрольная работа № 5 «Предел функции. Вычисление производной» Контрольная работа № 6 «Применение производной для исследования функций» Контрольная работа № 7 «Применение производной для решения задач» Приложения к рабочей программе алгебра 11 класс: Самостоятельные работы С1. Понятие корня п-ой степени из действительного числа. С2. Функция у= n x ,, их свойства и графики. С3,4. Свойства корня н-ой степени. С5, 6. Преобразование выражений, содержащих радикалы. С7,8 Обобщение понятия о показателе степени. С9. Степенные функции, их свойства и графики. С12, 13. Показательная функция, её свойства и график. С14, 15. Показательные уравнения С16 Показательные неравенства С17. Понятие логарифма С18, 19. Функция у=log x , её свойства и график. С20. Свойства логарифма. С21-22 Логарифмические уравнения. С23 Логарифмические неравенства. С24. Переход к новому основанию логарифма. С25,26. Дифференцирование показательной и логарифмической функций. С27. Первообразная. С28. Определённый интеграл. С29. Статистическая обработка данных. С30. Простейшие вероятностные задачи. С31. Сочетания и размещения. С32. Формула бинома Ньютона. С33. Случайные события и их вероятности. С34 Равносильность уравнений. С35. Общие методы решения уравнений С36. Решение неравенств с одной переменной. С37. Уравнения и неравенства с двумя переменными. С 38, 39 Системы уравнений. С 40, 41 Уравнения и неравенства с параметрами. Контрольные работы Контрольная работа № 1 «Функция у= n x , преобразование выражений, содержащих радикалы». Контрольная работа № 2 «Степенная и показательная функции» Контрольная работа № 3 «Логарифмическая функция, логарифмические уравнения» Контрольная работа № 4 «Логарифмические неравенства. Дифференцирование функций». Контрольная работа № 5 «Первообразная и интеграл». Контрольная работа № 6 « Решение уравнений и неравенств. МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «КОЗЛОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 3» АЛГЕБРА и начала математического анализа СТУПЕНЬ ОБУЧЕНИЯ: 2 КЛАСС: 10 - 11 . СРОК РЕАЛИЗАЦИИ ПРОГРАММЫ: 2 года. ПРИМЕРНАЯ ПРОГРАММА: Программа для общеобразовательных школ, гимназий, лицеев. Сборник «Математика. 5-11 кл.”/ Сост. Г.М.Кузнецова, Н.Г. Миндюк. – 3-е изд., стереотип.- М. Дрофа, 2002; 4-е изд. – 2004г./ рекомендовано Департаментом образовательных программ и стандартов общего образования МО РФ Ф.И.О. УЧИТЕЛЯ : ГЛУХИХ ЛАРИСА ВИКТОРОВНА. Рассмотрено на заседании ШМО протокол № _1 от «_29_»_08.__2011 г. Утверждено Директор МБОУ Н.Б.Матвеев Приказ №___от «__»_____2011 г.