Гончарова Ю., Особенности моделирования

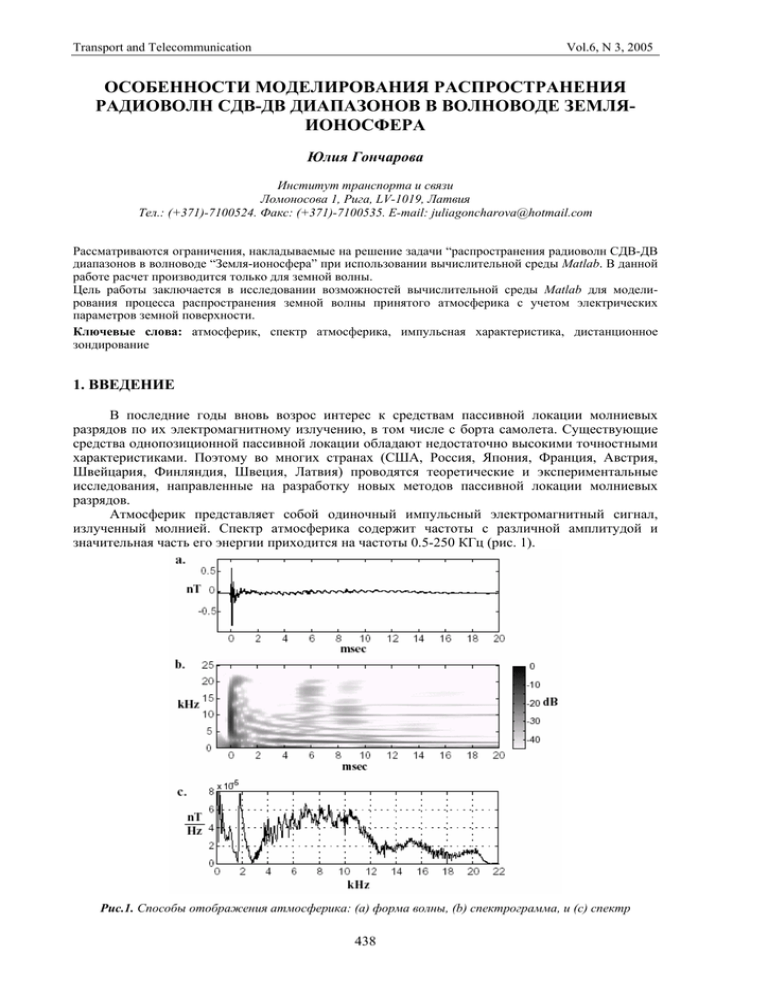
Transport and Telecommunication
Vol.6, N 3, 2005
ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ РАСПРОСТРАНЕНИЯ
РАДИОВОЛН СДВ-ДВ ДИАПАЗОНОВ В ВОЛНОВОДЕ ЗЕМЛЯИОНОСФЕРА
Юлия Гончарова
Инсmиmуm mранспорmа и связи
Ломоносова 1, Рига, LV-1019, Лаmвия
Тeл.: (+371)-7100524. Факс: (+371)-7100535. E-mail: [email protected]
Рассматриваются ограничения, накладываемые на решение задачи “распространения радиоволн СДВ-ДВ
диапазонов в волноводе “Земля-ионосфера” при использовании вычислительной среды Matlab. В данной
работе расчет производится только для земной волны.
Цель работы заключается в исследовании возможностей вычислительной среды Matlab для моделирования процесса распространения земной волны принятого атмосферика с учетом электрических
параметров земной поверхности.
Ключевые слова: атмосферик, спектр атмосферика, импульсная характеристика, дистанционное
зондирование
1. ВВЕДЕНИЕ
В последние годы вновь возрос интерес к средствам пассивной локации молниевых
разрядов по их электромагнитному излучению, в том числе с борта самолета. Существующие
средства однопозиционной пассивной локации обладают недостаточно высокими точностными
характеристиками. Поэтому во многих странах (США, Россия, Япония, Франция, Австрия,
Швейцария, Финляндия, Швеция, Латвия) проводятся теоретические и экспериментальные
исследования, направленные на разработку новых методов пассивной локации молниевых
разрядов.
Атмосферик представляет собой одиночный импульсный электромагнитный сигнал,
излученный молнией. Спектр атмосферика содержит частоты с различной амплитудой и
значительная часть его энергии приходится на частоты 0.5-250 КГц (рис. 1).
Рис.1. Способы отображения атмосферика: (а) форма волны, (b) спектрограмма, и (c) спектр
438
Proceedings of International Conference RelStat’04
Part 3
Атмосферик распространяется на большое расстояние путем многократного отражения
от Земли и нижних слоев ионосферы, т. е. в волноводе “Земля-ионосфера” [1], [2]. По форме
атмосферика, зафиксированного на определенном расстоянии от источника, можно судить о
характеристике трассы на этом расстоянии.
Форма импульсной характеристики определяется земной и ионосферными волнами.
Таким образом, расчет импульсной характеристики распадается на две задачи – моделирование
распространения земной волны и моделирование распространения ионосферных волн.
2. РАСПРОСТРАНЕНИЕ ЗЕМНОЙ ВОЛНЫ. ПОСТАНОВКА ЗАДАЧИ
И ОБЩЕЕ РЕШЕНИЕ
Постановка задачи о дифракции радиоволн вокруг гладкой сферической земной
поверхности при однородной атмосфере сводится к следующему. Земля считается идеально
гладкой электрически однородной сферой с радиусом а=6370 км, с относительной
диэлектрической проницаемостью ε2 и проводимостью σ2. Предполагается, что земная
атмосфера однородна и имеет относительную диэлектрическую проницаемость ε1=1 и
проводимость σ1=0. Относительная магнитная проницаемость земной поверхности и
атмосферы принимается равной единице: μ=1. При таком предположении процесс
распространения радиоволн определяется только дифракцией (огибанием) радиоволнами
земной поверхности [3].
3. МНОЖИТЕЛЬ ОСЛАБЛЕНИЯ
Для учета влияния поверхности Земли и неоднородности атмосферы на распространение
радиоволн вводят понятие множителя ослабления поля свободного пространства V (далее в
тексте – множитель ослабления).
Величина V есть отношение напряженности поля E на расстоянии r от передающей
антенны при распространении в реальных условиях к напряженности поля E0 на том же
расстоянии r при распространении в свободном пространстве, т. е.
V =
E
= V ⋅ e i⋅arg V ,
E0
(1)
где V – модуль множителя ослабления,
argV – его фаза.
Таким образом, V учитывает дополнительное ослабление амплитуды волны по сравнению с ее ослаблением в свободном пространстве, а argV – дополнительное изменение в фазе
волны.
Определение расчетной формулы для множителя ослабления производится по методу
В. А. Фока, т. е. путем решения соответствующей граничной задачи для полупроводящей
сферы. Формула для определения множителя ослабления при дифракции радиоволн вокруг
Земли с однородной атмосферой имеет вид [4]:
V ( x, y1 , y, q ) = e
где x
y
y1
w1(ts)
i⋅
π
4
e i⋅t s ⋅ x w1 (t s − y1 ) w1 (t s − y )
⋅
⋅
,
2
w1 (t s )
w1 (t s )
s =1 t s − q
∞
⋅2⋅ π ⋅ x ⋅∑
– расстояние в безразмерных единицах;
– высота приемной антенны в безразмерных единицах;
– высота передающей антенны в безразмерных единицах;
– функции Эйри;
439
(2)
Transport and Telecommunication
R
x= ' ;
R
R =
'
3
Vol.6, N 3, 2005
a2 ⋅ λ
π
1 3 a ⋅ λ2
h = ⋅
2
π2
h
y= ';
h
'
R – расстояние [м];
R′ – значение для расчета безразмерной величины x;
h′ – значение для расчета безразмерной величины y;
h – высота передающей антенны [м];
a – радиус Земли [м].
Следует отметить, что наиболее сложной задачей здесь является расчет суммы, которая
входит в выражение для множителя ослабления (2). Сложность заключается в ограниченной
точности вычисления функций Эйри, которые в среде Matlab рассчитываются через функции
Бесселя первого и второго рода порядка 1/3. Таким образом, точность расчета множителя
ослабления V определяется в основном точностью расчета функций Эйри, а также определением необходимого количества элементов суммы.
4. ПОСТОЯННАЯ ts
Постоянная t принимает дискретные собственные значения ts, являющиеся корнями
характеристического уравнения
w1' (t s ) − q ⋅ w1 (t s ) = 0 ,
(3)
где s – означает номер корня, w1' (t s ) есть производная от функции Эйри, а значение q будет
определено ниже.
Для определения корней ts было решено уравнение (3). Решение сводится к преобразованию данного уравнения в два других, одно из которых описывает действительную часть,
второе – мнимую. Эти уравнения решаются с помощью программы Matlab средствами
Optimization Toolbox. Начальные значения корней t0s получены из решения уравнения (3) при
q →0:
( )
w1' t s0 = 0 .
(4)
Все корни уравнения (4) имеют фазу π/3 и по модулю образуют возрастающую
последовательность при увеличении s. Первые три корня равны: t = 1.02 ⋅ e
0
1
t30 = 4.82 ⋅ e
i⋅
i⋅
π
3
, t = 3.25 ⋅ e
0
2
i⋅
π
3
,
π
3
, а последующие с хорошей точностью могут быть рассчитаны по формуле
⎡3 ⎛
3⎞ ⎤
t = ⎢ ⋅ ⎜ s − ⎟ ⋅π ⎥
4⎠ ⎦
⎣2 ⎝
0
s
2
3
i⋅
π
⋅e 3 .
(5)
5. ПАРАМЕТР q
Через параметр q учитываются электрические параметры земной поверхности. Значение
q может меняться в широких пределах. При вертикальной поляризации
440
Proceedings of International Conference RelStat’04
q = i⋅3
Part 3
1
π ⋅a
⋅
,
λ
ε 2 + i ⋅ 60 ⋅ σ 2 ⋅ λ
(6)
где ε2 – относительная диэлектрическая проницаемость [м];
σ2 – проводимость почвы [сим/м];
λ – длина волны [м].
Как видно из формулы, при очень длинных волнах и больших ε2 и σ2 величина q мала, а
при λ→0 q →∞.
При небольших q значения корней t0s совпадают с ts, но при увеличении q (с повышением
частоты) между этими корнями имеется существенное различие (рис. 2, a,b).
a.
b.
Рис.2. (а) действительная и (b) мнимая части корней t0s и ts
6. МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ ЗЕМНОЙ ВОЛНЫ
Величина множителя ослабления была рассчитана при разных значениях ε2 и σ2 для
типичных видов земной поверхности, а также при разных высотах приемных антенн.
Результаты представлены на рис.3, a. Для слабо проводящей среды (сухая почва, ε2=4,
σ2=0.001) множитель ослабления резко убывает с частотой. Для хорошо проводящей
поверхности (морская вода, ε2=80, σ2=5) множитель ослабления также убывает, но не столь
значительно.
Для высоты приемной антенны h=10 км (рис.3,b) величина множителя ослабления
перестает сильно зависеть от электрических параметров земной поверхности и практически
одинаково убывает с увеличением частоты.
441
Transport and Telecommunication
Vol.6, N 3, 2005
a.
b.
Рис.3. Множитель ослабления (а) при нулевых высотах антенн,
(b) для высоты приемной антенны h=10 км
7. ОЦЕНКА КОЛИЧЕСТВА ЭЛЕМЕНТОВ В СУММЕ ПРИ ЗАДАННОЙ
ТОЧНОСТИ
Построена зависимость количества элементов суммы при заданной точности определения
множителя ослабления (рис. 4,a). Из графика видно, что при нулевых высотах антенн на более
высоких частотах величина множителя ослабления определяется в основном только первыми
элементами суммы, в то время как для низких частот необходимо учитывать до двадцати
первых элементов суммы.
442
Proceedings of International Conference RelStat’04
Part 3
Для высоты приемной антенны h=10 км зависимость количества элементов суммы имеет
полностью противоположный вид, т. е. возрастает с частотой (рис. 4,b).
a.
b.
Рис.4. Количество элементов в сумме при заданной точности=0.01 (а) при
нулевых высотах антенн, (b) для высоты приемной антенны h=10 км
443
Transport and Telecommunication
Vol.6, N 3, 2005
8. ВЫВОДЫ
1. Учет электрических параметров земной поверхности, заложенных в параметре q,
существенно влияет на величину множителя ослабления V.
2. Поведение множителя ослабления V для разных высот антенн, при всех прочих равных
условиях, выглядит по-разному. При нулевой высоте приемной антенны количество элементов
в сумме убывает с увеличением частоты, в то время как при ненулевой высоте приемной
антенны количество элементов в сумме возрастает.
3. Вычисление множителя ослабления V становится затруднительным для частот выше 1
МГц. Это объясняется недостаточной точностью вычисления функций Эйри при больших
значениях параметра q. Необходимо разработать более совершенный метод решения
характеристического уравнения (6), позволяющий определять корни этого уравнения при
больших значениях параметра q.
[1] Cummer S. A. Lightning and ionospheric remote sensing using VLF/ELF radio atmospherics.
Dissertation,1997. – http://www-star.stanford.edu/~vlf/publications/theses/cummerthesis.pdf
[2] Cummer S. A. Ionospheric D region remote sensing using VLF radio atmospherics. Radio Science, 33,
1781–1792, November–December 1998. –
http://www.ee.duke.edu/~cummer/reprints/009_cummer98_radsci_dregion.pdf
[3] Черенков Е.Л., Чернышев О.В. Распространение радиоволн. Москва: Радио и связь, 1984. 272 с.
[4] Калинин А. И., Черенков Е.Л. Распространение радиоволн и работа радиолиний. Москва: Связь,
1971. 439 с.
444