Электростатика со льдом
реклама

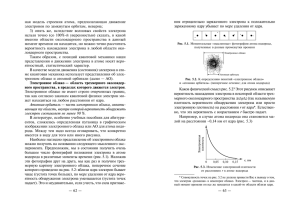
Ýëåêòðîñòàòèêà ñî ëüäîì À.ÑÒÀÑÅÍÊÎ « ÅÑËÈ ÁÛ Â ÂÀØÅÌ ÒÅËÅ ÈËÈ Â ÒÅËÅ ÂÀØÅÃÎ ÑÎÑÅÄÀ (ñòîÿùåãî îò âàñ íà ðàññòîÿíèè âûòÿíóòîé ðóêè) ýëåêòðîíîâ îêàçàëîñü áû âñåãî íà 1% áîëüøå, ÷åì ïðîòîíîâ, òî ñèëû îòòàëêèâàíèÿ õâàòèëî áû, ÷òîáû ïîäíÿòü «âåñ», ðàâíûé âåñó íàøåé Çåìëè!» («Ôåéíìàíîâñêèå ëåêöèè ïî ôèçèêå»). À âîçìîæíî ëè òàêîå? È òóò Îòëè÷íèê âñïîìíèë íåäàâíèå «ëåäÿíûå äîæäè», èçëîìàâøèå òûñÿ÷è äåðåâüåâ â Ðîññèè è ïîðâàâøèå êèëîìåòðû ýëåêòðîïðîâîäîâ. Îí çíàë òàêæå î òîì, ÷òî â îäíîé òîëüêî Àìåðèêå â ðåçóëüòàòå îáëåäåíåíèÿ íåáîëüøèõ ñàìîëåòîâ åæåãîäíî ïîãèáàþò äåñÿòêè ÷åëîâåê, à ìàòåðèàëüíûé óùåðá ñîñòàâëÿåò ïî÷òè ìèëëèàðä äîëëàðîâ. È åìó ïðèøëà â ãîëîâó ñâåòëàÿ ìûñëü: åñëè õîëîäíûå îáëà÷íûå êàïëè, óäàðÿþùèåñÿ î ïîâåðõíîñòü ñàìîëåòà, ýëåêòðè÷åñêè çàðÿæåíû, òî, îáðàçóÿ ëåäÿíóþ êîðêó (÷òî î÷åíü ïëîõî), îíè ìîãëè áû îäíîâðåìåííî è ðàçðóøàòü åå (÷òî áûëî áû õîðîøî). È Îòëè÷íèê íà÷àë ðàññóæäàòü. Ïðåäñòàâèì ñåáå òîíêóþ äèýëåêòðè÷åñêóþ ïëåíêó ïëîùàäüþ S, íà êîòîðîé ðàâíîìåðíî «ðàçìàçàí» ýëåêòðè÷åñêèé çàðÿä q, òàê ÷òî ïîâåðõíîñòíàÿ ïëîòíîñòü çàðÿäà ðàâíà σ = q S . Áóäåì ñ÷èòàòü, íàïðèìåð, ÷òî ýòîò çàðÿä îòðèöàòåëüíûé: êòî-òî «íàïûëèë» ýëåêòðîíû íà ïîâåðõíîñòü ïëåíêè. Òîãäà íàïðÿæåííîñòü ýëåêòðè÷åñêîãî ïîëÿ áóäåò íàïðàâëåíà òàê, êàê èçîáðàæåíî íà ðèñóíêå 1,à, à çíà÷åíèå ïîëÿ E = ±σ (2ε0 ) ïðåäñòàâëåíî íà ãðàôèêå íà ðèñóíêå 1,á. Âèäíî, ÷òî âñå âåêòîðû E íàïðàâëåíû íîðìàëüíî ê ïëåíêå, à âåëè÷èíà Å ïðè ïåðåñå÷åíèè ïëåíêè â íàïðàâëåíèè îñè õ ïðåòåðïåâàåò ñêà÷îê, íàïðàâëåííûé âíèç è ðàâíûé −σ ε0 . Êàê òóò íå âñïîìíèòü ïëîñêèé êîíäåíñàòîð! Äåéñòâèòåëüíî, åñëè ìû ïîäíåñåì ê íàøåé îòðèöàòåëüíî çàðÿæåííîé ïëåíêå òàêóþ æå, íî ïîëîæèòåëüíî çàðÿæåííóþ ïëåíêó ñ òàêîé æå ïî ìîäóëþ ïîâåðõíîñòíîé ïëîòíîñòüþ çàðÿäà (ðèñ.1,â,ã), òî ïîëå ìåæäó ýòèìè ïëîñêîñòÿìè (h/2 < x < < h/2) óäâîèòñÿ: E = σ ε0 , à ñíàðóæè èñ÷åçíåò. Äàëåå, íà äàâëåíèå: F σ2 ε E2 = = 0 . (1) S 2ε0 2 Ñ äðóãîé ñòîðîíû, ýòó âåëè÷èíó ìîæíî ðàññìàòðèâàòü è êàê îáúåìíóþ ïëîòíîñòü ýíåðãèè ýëåêòðè÷åñêîãî ïîëÿ äîñòàòî÷íî óáåäèòüñÿ â òîì, ÷òî ýòè ôèçè÷åñêèå ïîíÿòèÿ èìåþò îäíó è òó æå ðàçìåðíîñòü: [F ] [S ] = H ì2 = Äæ ì 3 . Óìåñòíî âñïîìíèòü, ÷òî ïîíÿòèå ïîëÿ è åãî ôèçè÷åñêèõ àòðèáóòîâ ââåë Ìàéêë Ôàðàäåé â ïåðâîé ïîëîâèíå äåâÿòíàäöàòîãî âåêà. Èäåÿ ïîëÿ ñ÷èòàåòñÿ ñàìûì âàæíûì îòêðûòèåì ñî âðåìåí Íüþòîíà. «Íàäî èìåòü ìîãó÷èé äàð íàó÷íîãî ïðåäâèäåíèÿ, ïèñàë À. Ýéíøòåéí, ÷òîáû ðàñïîçíàòü, ÷òî â îïèñàíèè ýëåêòðè÷åñêèõ ÿâëåíèé íå çàðÿäû è íå ÷àñòèöû îïèñûâàþò ñóòü ÿâëåíèé, à ñêîðåå ïðîñòðàíñòâî ìåæäó çàðÿäàìè è ÷àñòèöàìè». Íî âåðíåìñÿ ê íàøåé ðàâíîìåðíî çàðÿæåííîé ïëåíêå. Ïðåäñòàâèì òåïåðü (ðèñ.2), ÷òî ïëåíêà âîâñå íå áåñêîíå÷íî òîíêàÿ (äà òàêóþ è íåãäå äîñòàòü), à èìååò òîëùèíó h, à òîò æå ñàìûé çàðÿä q «ðàçìàçàí» ðàâíîìåðíî óæå ïî åå îáúåìó Sh òàê, ÷òî îáúåìíàÿ ïëîòíîñòü çàðÿäà ñòàëà ðàâíîé δ = q ( Sh ) = σ h . Ïîíÿòíî, ÷òî âíå ýòîé «òîíêîé ïëåíêè», êîòîðóþ ìîæíî òåïåðü íàçâàòü ñëîåì òîëùèíîé h, íàïðàâëåíèå è âåëè÷èíà ýëåêòðè÷åñêîãî ïîëÿ íå èçìåíÿåòñÿ (ñì. òàêæå Ðèñ. 2 ðèñ.1,á). À âíóòðè? Ðàçóìíî ïðåäïîëîæèòü, ÷òî ïîëå âíóòðè ñëîÿ áóäåò èçìåíÿòüñÿ íåïðåðûâíî ìåæäó åãî çíà÷åíèÿìè íà ïîâåðõíîñòè ñëîÿ, ïðè÷åì ëèíåéíî íó õîòÿ áû ïîòîìó, ÷òî â ñðåäíåé ïëîñêîñòè (õ = 0) çíà÷åíèå íàïðÿæåííîñòè äîëæíî îáðàòèòüñÿ â íîëü (ïî ñîîáðàæåíèÿì ñèììåòðèè). Ïîäíåñåì òåïåðü (ðèñ.3,à) ê ýòîìó ñëîþ ñïðàâà ìåòàëëè÷åñêèé öèëèíäð ñ ïëîñêèì òîðöîì, è ïóñòü ðàäèóñ ýòîãî p= Ðèñ. 3 Ðèñ. 1 êàæäóþ èç ýòèõ äâóõ ïëîñêîñòåé, íåñóùèõ çàðÿäû ±σS è íàõîäÿùèõñÿ â ïîëå äðóãîé ïëîñêîñòè ñ íàïðÿæåííîñòüþ ±σ (2ε0 ) , äåéñòâóåò ñèëà ïðèòÿæåíèÿ âåëè÷èíîé F = σS ⋅ σ (2ε0 ) , êîòîðóþ ìîæíî òðàêòîâàòü è êàê âíåøíåå öèëèíäðà ìíîãî áîëüøå òîëùèíû ñëîÿ, òàê ÷òî ïîâåðõíîñòü ýòîãî öèëèíäðà «áåñêîíå÷íî äàëåêà» îò ðàññìàòðèâàåìîé êàðòèíû ñ õàðàêòåðíûì ðàçìåðîì h, ïîìåùàþùåéñÿ íà íàøèõ ðèñóíêàõ. Äà, íî âåäü âíóòðè ìåòàëëà ýëåêòðè÷åñêîå ïîëå ðàâíî íóëþ (èíà÷å â ìåòàëëå ïîáåæàë áû ýëåêòðè÷åñêèé òîê). À ýòî îçíà÷àåò, ÷òî íà ïîâåðõíîñòè òîðöà äîëæåí âîçíèêíóòü ðàñïðåäåëåííûé ïîëîæèòåëüíûé çàðÿä ñ ïëîò- ØÊÎËÀ íîñòüþ, â òî÷íîñòè ðàâíîé σ (ïî ìîäóëþ). Ýëåêòðè÷åñêîå ïîëå îò ýòîãî ðàñïðåäåëåííîãî çàðÿäà àíàëîãè÷íî ïåðâîíà÷àëüíîìó (ñì. ðèñ.2), òîëüêî ïðîòèâîïîëîæíî ïî çíàêó (îíî îòäåëüíî èçîáðàæåíî íà ðèñ.1,â,ã), òàê ÷òî âíå ñëîÿ ñóììàðíàÿ íàïðÿæåííîñòü ïîëÿ ñòàíåò ðàâíîé íóëþ (ðèñ.3,á). Íî ïðè ÷åì òóò ëåä, îáåùàííûé âûøå? À ïðè òîì, ÷òî ïîðà ó÷åñòü, ÷òî íàøè ïåðâîíà÷àëüíûå çàðÿäû ñ îáúåìíîé ïëîòíîñòüþ δ = σ h äîëæíû áûòü âìîðîæåíû â äèýëåêòðèê, ò.å. â ñðåäó, íå îáëàäàþùóþ ñâîéñòâîì ýëåêòðîïðîâîäíîñòè, à âåäü ìû äî ñèõ ïîð ñ÷èòàëè, ÷òî îíè «ðàçâåøåíû» êåì-òî â âàêóóìå. Íî åñëè ñëîé îáëàäàåò äèýëåêòðè÷åñêîé ïðîíèöàåìîñòüþ ε , òî íàïðÿæåííîñòü ýëåêòðè÷åñêîãî ïîëÿ Ei â íåì äîëæíà áûòü óìåíüøåíà â ε ðàç (ñì. ðèñ.3,á, ïóíêòèð): Ei = E ε (òóò èíäåêñ i ïðîèñõîäèò, åñëè õîòèòå, îò inner âíóòðåííåå èëè, åñëè õîòèòå, îò ice ëåä). Âèäíî, ÷òî íàèáîëüøåå çíà÷åíèå ýòîãî ïîëÿ ðàâíî σ δh Emax = = . (2) ε 0ε ε 0ε Êàêóþ ïîëüçó ìîæíî èçâëå÷ü èç íàøèõ ðàññóæäåíèé? À âîò êàêóþ: ìîæíî îöåíèòü âíóòðåííèå ñèëû, äåéñòâóþùèå â ñëîå ëüäà. Äåéñòâèòåëüíî, åñëè ïîëþ â âàêóóìå ìåæäó äâóìÿ çàðÿæåííûìè ïëîñêîñòÿìè ìû ïðèïèñàëè ñâîéñòâî îêàçûâàòü äàâëåíèå, òî ïî÷åìó áû è â ñëó÷àå ñ çàðÿæåííûì äèýëåêòðèêîì íå ïðèïèñàòü ïîëþ òî æå ñâîéñòâî? Òîëüêî òåïåðü â ôîðìóëó (1), êàçàëîñü áû, ðàçóìíî äîáàâèòü ìíîæèòåëü (ε − 1) âåäü ïðè ε → 1 èñ÷åçàåò ñàì äèýëåêòðèê. Îäíàêî òóò äåëî ñëîæíåå. Õîòÿ ïðè ε → 1 äèýëåêòðèê è ïðåâðàùàåòñÿ â âàêóóì, íàïðÿæåíèå íå ìîæåò èñ÷åçíóòü: âåäü êòî-òî äîëæåí óäåðæèâàòü âìåñòå çàðÿäû îäíîãî çíàêà. Áîëåå òî÷íàÿ òåîðèÿ ãîâîðèò î òîì, ÷òî íóæíî ââåñòè ìíîæèòåëü 2ε − 1 (âïðî÷åì, ýòî íå ïîâëèÿåò íà ïîðÿäîê âåëè÷èíû èñêîìîé îöåíêè). Ñòðîãî ãîâîðÿ, ñèëû âíóòðè çàðÿæåííîãî äèýëåêòðèêà ðàçëè÷íû â ðàçíûõ íàïðàâëåíèÿõ.  øèðîêî èçâåñòíîì ó÷åáíèêå È.Å.Òàììà «Îñíîâû òåîðèè ýëåêòðè÷åñòâà», âûäåðæàâøåì ïîðÿäêà äåñÿòêà èçäàíèé è ñûãðàâøåì áîëüøóþ ðîëü â ïîäãîòîâêå îòå÷åñòâåííûõ ôèçèêîâ â ïîñëåäíèå ïÿòüäåñÿò ëåò, îá ýòîì ñêàçàíî âåñüìà îáðàçíî: «ìîæíî ïðåäñòàâèòü ñåáå, ÷òî âäîëü ñèëîâûõ ëèíèé ïîëÿ íàòÿíóòû óïðóãèå íèòè, ïîäâåðæåííûå íàòÿæåíèþ è îêàçûâàþùèå äðóã íà äðóãà áîêîâîå äàâëåíèå». Èòàê, äëÿ íàøèõ îöåíîê ïðèìåì, ÷òî íàèáîëüøåå ìåõàíè÷åñêîå íàïðÿæåíèå âíóòðè ðàâíîìåðíî çàðÿæåííîãî äèýëåê2 ε0 (2ε − 1) 2 , èëè, èñïîëüçóÿ ôîðìóëó (2), òðèêà ðàâíî Emax pmax = δ2 (2ε - 1) h2 . 2ε0ε2 (3) Ïóñòü òåïåðü ðèñóíîê 3,à èçîáðàæàåò ñëîé ëüäà, íàëèïøèé íà ïîâåðõíîñòü êàêîãî-ëèáî ýëåìåíòà êîíñòðóêöèè ñàìîëåòà (íàïðèìåð, ïåðåäíþþ êðîìêó êðûëà), è ïóñòü â ïåðåîõëàæäåííîì îáëàêå, â êîòîðîì äâèæåòñÿ ñàìîëåò, ðàñïðåäåëåíû ìåòàñòàáèëüíûå (ãîòîâûå çàìåðçíóòü) êàïëè ñ êîíöåíòðàöèåé n è ðàäèóñîì à. Òîãäà ìàññîâàÿ ïëîòíîñòü êàïåëü â îáëàêå ðàâíà 4 ρ∞ = n ⋅ πa 3ρ0 , 3 ãäå ρ0 ïëîòíîñòü âîäû. Äàëåå, äîïóñòèì (äëÿ ÷èñëåííîé îöåíêè ñâåðõó), ÷òî êàæäàÿ êàïëÿ íåñåò ìàêñèìàëüíî âîçìîæíûé çàðÿä, îïðåäåëåííûé ïðåäåëüíûì çíà÷åíèåì íàïðÿæåííîñòè ýëåêòðè÷åñêîãî ïîëÿ E∗ íà åå ïîâåðõíîñòè, âûøå êîòîðîãî â âîçäóõå íà÷íåòñÿ ñòåêàíèå çàðÿäà ñ ïîâåðõíîñòè êàïëè. Òîãäà, ñîãëàñíî çàêîíó Êóëîíà, ýòîò çàðÿä ðàâåí Q = E∗ ⋅ 4πa2ε0 .  «ÊÂÀÍÒÅ« Ïðè îáðàçîâàíèè íàëåäè ïðîèçîéäåò óïëîòíåíèå â ρi ρ∞ ðàç, ãäå ρi ìàññîâàÿ ïëîòíîñòü ëüäà. Ïîýòîìó îáúåìíàÿ ïëîòíîñòü çàðÿäà ñòàíåò ðàâíîé ρi ρ∞ ρ 3ρ ε E = E∗ ⋅ 4πa2ε0 i = i 0 ∗ . 4 ρ∞ ρ∞ ρ0 a πa 3ρ0 3 (Ëþáîïûòíî îòìåòèòü, ÷òî ðåçóëüòàò îêàçàëñÿ íå çàâèñÿùèì îò «âîäíîñòè» îáëàêà ρ∞ , ÷òî, âïðî÷åì, âïîëíå ïîíÿòíî. Îáúåìíàÿ ïëîòíîñòü çàðÿäà â íàëåäè òàêàÿ æå, êàê â êàæäîé êàïëå, ñ ïîïðàâêîé íà îòëè÷èå ïëîòíîñòè ëüäà îò ïëîòíîñòè âîäû.) Ïîäñòàâëÿÿ âñå ýòî â âûðàæåíèå (3), ïîëó÷èì δ = nQ 3ρ ε E pmax = i 0 ∗ ρ0 a 2 (2ε − 1) h2 2ε0ε2 = 9 ρi E∗ 2 ρ0 a 2 (2ε − 1) ε0h2 ε2 . Îñòàëîñü òîëüêî ñäåëàòü ÷èñëåííóþ îöåíêó. Ïðèìåì ρi = 900 êã ì 3 , ρ0 = 1000 êã ì3 , E∗ = 3 ⋅ 106  ì , à = 9 = 10 ìêì = 10−5 ì , ε = 100 , 1 (4πε0 ) = 9 ⋅ 10 Ô ì , h = = 1 ñì = 10−2 ì , òîãäà pmax = 9 9 ⋅ 1012 2 ⋅ 10−4 9 7 ⋅ Ïà = 10 Ïà . −10 2 10 4π 4π ⋅ 9 ⋅ 109 ⋅ 102 Ýòî çíà÷åíèå âïîëíå ñðàâíèìî ñ èçìåðåííûìè â ëàáîðàòîðíûõ óñëîâèÿõ ïðåäåëàìè ïðî÷íîñòè ëüäà. Âîò òîëüêî ëåòàòü â òàêèõ îáëàêàõ íå ðåêîìåíäóåòñÿ. Êîíå÷íî, ðàññìîòðåííàÿ ãåîìåòðèÿ ìàëî ïîõîæà íà ïåðåäíþþ êðîìêó êðûëà.  ñëåäóþùåì ïðèáëèæåíèè ìîæíî áûëî áû ðàññìîòðåòü öèëèíäð, ó÷åñòü, ÷òî ëèíèè òîêà âîçäóõà è òðàåêòîðèè êàïåëü èçãèáàþòñÿ ïåðåä íèì (ýòî ñâÿçàíî ñ èçâåñòíîé òåîðåìîé Í.Å.Æóêîâñêîãî), è ðåøèòü ÷èñëåííî áîëåå ñëîæíóþ çàäà÷ó. Íî òóò äðóãàÿ ìûñëü ïðèøëà â ãîëîâó Îòëè÷íèêà: ïîñêîëüêó ëåä è âîäà (äàæå äèñòèëëèðîâàííàÿ) îáëàäàþò ýëåêòðîïðîâîäíîñòüþ, çàðÿä ìîæåò ñòåêàòü èç íàëåäè â ïðîâîäíèê! Âåðíåìñÿ ê êîíäåíñàòîðó, çàïîëíåííîìó âåùåñòâîì ñ äèýëåêòðè÷åñêîé ïðîíèöàåìîñòüþ ε è óäåëüíîé ïðîâîäèìîñòüþ (âåëè÷èíîé, îáðàòíîé óäåëüíîìó ñîïðîòèâëåíèþ) λ . ßñíî, ÷òî, ÷åì áîëüøå ε , òåì áîëüøèé çàðÿä ìîæíî íàêîïèòü íà ïëàñòèíàõ (âåäü åìêîñòü êîíäåíñàòîðà ïðîïîðöèîíàëüíà εε0 ), à ÷åì áîëüøå λ , òåì ñêîðåå êîíäåíñàòîð ðàçðÿäèòñÿ. Îòñþäà î÷åâèäíî, ÷òî õàðàêòåðíîå âðåìÿ ðàçðÿäêè ðàâíî τ = εε0 λ (ïðîâåðüòå ðàçìåðíîñòü!). Ïðèíèìàÿ ε = 100, λ = 10−6 1 (Îì ⋅ ì ) , ïîëó÷èì τ = 10 −3 ñ . Çíà÷èò, çàðÿä ïî÷òè ìãíîâåííî áóäåò óõîäèòü èç íàëåäè. Äà, íî ïðè ýòîì äîëæíî âûäåëÿòüñÿ äæîóëåâî òåïëî... Ý, áðàò, ïîäóìàë Îòëè÷íèê, ÷òîáû âî âñåì ýòîì ðàçîáðàòüñÿ, íóæíî ïîñòóïèòü íà ôàêóëüòåò àýðîìåõàíèêè è ëåòàòåëüíîé òåõíèêè Ìîñêîâñêîãî ôèçèêî-òåõíè÷åñêîãî èíñòèòóòà è ñ óñïåõîì åãî çàêîí÷èòü. ×åãî âàì è æåëàåì!