Равновесие твердого тела
реклама
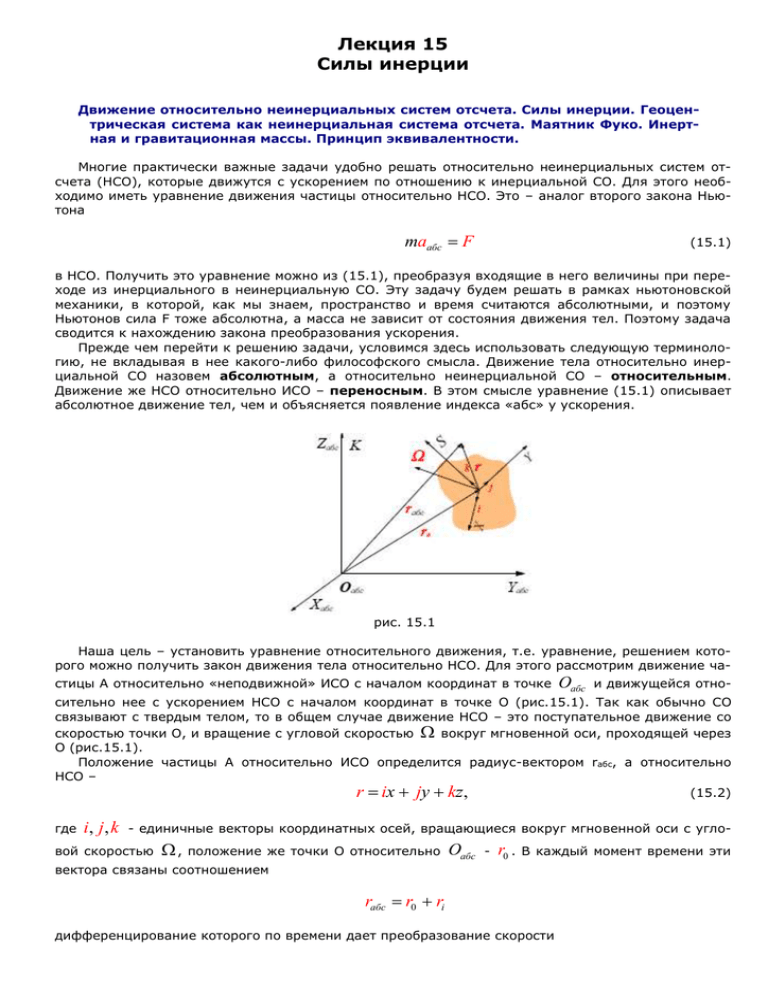
Лекция 15 Силы инерции Движение относительно неинерциальных систем отсчета. Силы инерции. Геоцентрическая система как неинерциальная система отсчета. Маятник Фуко. Инертная и гравитационная массы. Принцип эквивалентности. Многие практически важные задачи удобно решать относительно неинерциальных систем отсчета (НСО), которые движутся с ускорением по отношению к инерциальной СО. Для этого необходимо иметь уравнение движения частицы относительно НСО. Это – аналог второго закона Ньютона maабс F (15.1) в НСО. Получить это уравнение можно из (15.1), преобразуя входящие в него величины при переходе из инерциального в неинерциальную СО. Эту задачу будем решать в рамках ньютоновской механики, в которой, как мы знаем, пространство и время считаются абсолютными, и поэтому Ньютонов сила F тоже абсолютна, а масса не зависит от состояния движения тел. Поэтому задача сводится к нахождению закона преобразования ускорения. Прежде чем перейти к решению задачи, условимся здесь использовать следующую терминологию, не вкладывая в нее какого-либо философского смысла. Движение тела относительно инерциальной СО назовем абсолютным, а относительно неинерциальной СО – относительным. Движение же НСО относительно ИСО – переносным. В этом смысле уравнение (15.1) описывает абсолютное движение тел, чем и объясняется появление индекса «абс» у ускорения. рис. 15.1 Наша цель – установить уравнение относительного движения, т.е. уравнение, решением которого можно получить закон движения тела относительно НСО. Для этого рассмотрим движение частицы А относительно «неподвижной» ИСО с началом координат в точке Oабс и движущейся отно- сительно нее с ускорением НСО с началом координат в точке О (рис.15.1). Так как обычно СО связывают с твердым телом, то в общем случае движение НСО – это поступательное движение со скоростью точки О, и вращение с угловой скоростью вокруг мгновенной оси, проходящей через О (рис.15.1). Положение частицы А относительно ИСО определится радиус-вектором rабс, a относительно НСО – r ix jy kz, (15.2) где i, j , k - единичные векторы координатных осей, вращающиеся вокруг мгновенной оси с угло- вой скоростью , положение же точки О относительно Oабс - r0 . В каждый момент времени эти вектора связаны соотношением rабс r0 ri дифференцирование которого по времени дает преобразование скорости Вычислим vабс v0 r (15.3) r i x j y k z i x j y k z vотн [r ] , (15.4) r: где учитывали, что единичные векторы i, j , k вращаются с угловой скоростью , т.е. i [i], j [j ], k [k ]. (15.5) В формуле (15.4) член vотн i x j y k z есть скорость частицы в той СО, относительно которой орты (15.6) i, j , k покоятся, т.е. НСО. Поэтому (15.6) есть относительная скорость частицы. Подставляя (15.4) и (15.6) в (15.3), получим преобразование скорости в окончательном виде: vабс vотн vo [r ] vотн vпер . Здесь vпер vo [r ] (15.7) есть скорость НСО в точке А, т.е. является переносной скоростью. Следовательно, абсолютная скорость равна векторной сумме переносной и относительной скоростей частицы. Для получения закона преобразования ускорения, продифференцируем (15.7) по времени: v абс аабс vотн v пер . (15.8) Вычислим производные в правой части в отдельности: v пер vo [ r ] [ r ] ao [ r ] [vотн ] [[r ]] . Здесь пользовались формулой (.4). С учетом (.5) и (.6) получим vотн i x j y k z i x j y k z aотн [vотн ] , где аотн i x j y k z (15.9) - относительное ускорение частицы, в котором орты i,j,k считаются неизменными. Подставляя полученные представления в (17.8), окончательно получим следующий закон преобразования ускорения: aабс ao [ r ] 2 r aотн 2[vотн ] aпер аотн аkор , где двойное векторное произведение раскрыто по правилу «бац-цаб», мгновенной оси вращения составляющая радиус-вектора, ао v0 - r - (15.10) перпендикулярная к ускорение поступательного движения НСО, ε – ее угловое ускорение, апер ao [ r ] 2 r - переносное ускорение, которая бы имела покоящаяся относительно НСО частица. Последний член – (15.11) аkор 2[vотн ] , (15.12) называется кориолисовым ускорением в честь французского ученого Кориолиса (1792-1843). Преобразование (15.10) выражает теорему Кориолиса: абсолютное ускорение равно векторной сумме относительного, переносного и кориолисова ускорений. Подставим теперь выражение (15.10) в уравнение (15.1) и перенесем члены, содержащие апер и акор , в правую часть: mаотн F mапер mакор . (15.13) Это и есть искомое уравнение движения частицы относительно произвольной НСО. Для физического истолкования полученного результата, обобщим понятие силы, считая, что сила - причина ускорения частицы относительно любой системы отсчета (а не только инерциальной, как считали до сих пор). При такой трактовке, всю правую часть уравнения (15.13) следует считать силой, действующей на частицу в НСО. Она состоит из двух совершенно разных составляющих. Первая – Ньютонов сила F, которая действует на частицу и в ИСО и является результатом взаимодействия тел. Мы показали, что в рамках абсолютности пространства и времени, будучи зависящей от относительного положения и относительной скорости взаимодействующих тел, эта сила инвариантна при переходе в другие системы отсчета. Совершенно иной представляется вторая составляющая: mапер mакор , которая возникает не из-за взаимодей- ствия тел, а из-за ускоренного движения системы отсчета и называется силой инерции. Она представляет сумму переносных сил инерции: Fпер вой силы инерции: mапер , и так называемой, кориолисо- Fкор mакор . Силы инерции не подчиняются третьему закону Ньютона. Если на тело действует сила инерции, то не следует искать другое тело, на которое приложена противодействующая сила. В этом смысле движение под действием сил инерции аналогично движению во внешних силовых полях. Сила инерции является всегда внешней силой по отношению к любой движущейся системе материальных тел. Другая особенность силы инерции заключается в том, что она меняется при переходе в другие НСО и, в частности, исчезают в ИСО, т.е. силы инерции не инвариантны относительно переходам в другие СО. Далее, заметим, что все силы инерции пропорциональны инертной массе тела. В раскрытом виде уравнение движения в произвольной НСО, с учетом (15.11) и (15.12), имеет следующий вид: m dv F mao m[r ] m2 r 2m[v] , dt (15.14) где опущен индекс «отн», так как речь идет об относительном движении. Из уравнения (15.14) видно, что силы инерции слагаются из четырех составляющих, первые три которых представляют переносные силы инерции, в состав которой входят: - поступательная сила инерции: Fп ma0 , (15.15) которая действует на все тела в поступательно движущихся НСО и направлена противоположно к ее ускорению a0 . Например, когда транспорт набирает скорость, пассажиры испытывают дей- ствие силы, направленной против движения транспорта. Рис. 15.2 При торможении транспорта, эта сила направлена в сторону его движения. Это и есть поступательная сила инерции. Если в ускоренно движущем вагоне поезда висит маятник (рис.15.2), то эта сила отклоняет его в сторону, противоположную ускорению, и при относительном равновесии маятник отклонен от вертикали на угол arctg (a0 / g ) . - центробежная сила инерции (или просто центробежная сила): Fцб m2 r (15.16) действует на тела во вращающихся НСО, которая стремится удалять тела от оси вращения. Она тем больше, чем дальше отстоит тело от оси вращения. Это наглядно демонстрируется на следующем примере. Если на центробежной машине подвесить несколько шариков и привести машину во вращение, то центробежные силы отклоняют шарики от оси вращения тем больше, чем дальше отстоит шарик от оси. Действию центробежной силы подвергаются, например, пассажиры в движущемся транспорте на поворотах, летчики при выполнении фигур высшего пилотажа. Эти силы используются в центробежных сушилках, в сепараторах; - сила инерции, вызванная неравномерностью вращения НСО, назовем ее тангенциальной силой инерции: F m[r ] Четвертая – кориолисова сила инерции (или просто кориолисова сила) Fkop m[v] (15.17) которая действует перпендикулярно к относительной скорости тела, движущегося во вращающейся СО, и поэтому искривляет его траекторию. Очевидно, эта сила является гироскопической и не совершает работу. Если тело покоится во вращающейся НСО, то на него Кориолисов сила не действует. Оно лишь подвергается действия центробежной силы. Как тело начнет двигаться (в отличном от направлении), оно будет подвергаться еще и действия кориолисовой силы. Вот почему удержаться в транспорте на поворотах легче в неподвижном положении, чем при движении. Рис. 15.3 Действие силы Кориолиса можно демонстрировать на вращающемся вокруг вертикальной оси диске, покрытой белой бумагой. Если погрузить шар в чернило, а затем, положив на центр диска сообщить скорость v в горизонтальном направлении, заметим, что хотя относительно лаборатории шар перемещается к краю диска прямолинейно, на бумагу он оставляет кривой след (рис.15.3). Действительно, в СО, связанной с лабораторией, на шар действуют силы тяжести и ре- акции опоры, которые компенсируют друг друга, поэтому здесь движение прямолинейное. В СО, связанной с диском, на движущий шар действует также кориолисова сила 2mvΩ, направленная перпендикулярно скорости шара, в плоскости диска, которая и искривляет траекторию шара относительно диска. Система отсчета, связанная с Землей, как НСО. Как известно, связанная с Солнцем СО (Гелиоцентрическая СО) является инерциальной. Земля обращается вокруг Солнца с ускорением поступательного движения ное вращение с угловой скоростью 2 / 24 3600 рад / с а и совершает суточ- вокруг своей оси. Так что связанная с Землей СО (Геоцентрическая СО), является неинерциальной. Поместим начало координат в центре Земли, а координатные оси жестко свяжем с Землей (рис.15.4). Рис. 15.4 Так что в уравнении (15.14) ао а , a из-за практически равномерного вращения Земли третий член в (15.14) равен нулю. Ньютонов силу F представим в виде суммы трех сил: F F F , где первая – гравитаци- онное притяжение Земли, второе - равнодействующая сил гравитационного притяжения Солнца, Луны, планет и прочих небесных тел, третья – геометрическая сумма всех остальных сил не гравитационного происхождения (сила сопротивления воздуха, трения, натяжения нити, реакции опоры, электрических и магнитных полей и прочие). Тогда уравнение (15.14) можно представить в виде: ma ( F ma ) F ( F m2 r ) 2m[v]. (15.18) Воспользуемся обобщенным законом Галилея о том, что в малой области гравитационного поля, независимо от их массы, все тела падают с одинаковым ускорением. Это очевидным образом следует из того факта, что гравитационные силы, как и силы инерции, строго пропорциональны массе тела. Так как размеры Земли очень малы по сравнению с расстояниями Солнца, Луны и прочих небесных тел, то создаваемое ими гравитационное поле в малой окрестности Земли можно считать однородным. Поэтому в принятом приближении это поле частице А сообщает такое же ускорение, что и центру Земли, т.е. а . Значит F ma , и первая скобка в правой части урав- нения (15.18) обращается в нуль. Итак, гравитационное действие всех небесных тел, кроме Земли, полностью компенсируется поступательной силой инерции, возникающей из-за ускорения, сообщаемой этими телами Земле. Именно этот факт (а не малость!) является причиной того, что при рассмотрении движений тел околоземной поверхности мы пренебрегаем действием Солнца, Луны и прочих небесных тел. Рассмотрим теперь вторую скобку в (15.18). Учитывая, что гравитационное притяжение Земли тоже пропорционально массе частицы А и выражается формулой F mg , где g - ускорение свободного падения при отсутствии вращения Земли, введем обозначение F m2 r mg , где g g 2 r . (15.19) В окончательном виде уравнение относительного движения в Геоцентрической системе отсчета будет m dv F mg 2m[v]. dt (15.20) Рассмотрим сначала равновесие тела, лежащего на подставке, или подвешенного за подвес. Так как при этом v =0, a =0, то из (15.20) находим F mg . В первом случае F – реакция опоры N , а во втором – натяжение нити T (рис.15.5). рис. 15.5 рис. 15.6 Введем определение: весом тела назовем приложенной к нему силе найдем P F . Так что для P P mg . Учитывая (15.19), видим, что вес тела состоит из двух слагаемых – гравитационного притяжения Земли и центробежной силы инерции: P mg m2 r . (15.21) Если тело подвешено на нити, то направление нити определяет направление силы Р, следовательно и ускорения g. Оно называется направлением подвеса. Заметим, что из-за центробежной силы это направление отличается от направления симметричной. Действительно, при этом g g , даже если бы Земля была сферически был бы направлен к центру Земли, а направление от- веса на географической широте θ, определяемое вектором g - отклоненной от направления к центру Земли на малый угол (рис.15.6) sin 2 r / g sin 2 R / g cos sin . (15.22) Этот угол обращается в нуль на полюсах и экваторе. Реальная Земля (опять по причине вращения) слегка сплюснута вдоль оси вращения, но и в этом случае формула (15.22) , хотя и приближенно, но является достаточно точной. Проектируя векторы g и 2 r на направление вектора g , получим g g cos 2 r cos g 2 R cos 2 , где R - радиус Земли. Точные измерения величины g (15.23) 983,2 см / с 2 и g : на полюсе на полюсе дают значение 978,0 см / с 2 . Тогда по формуле (15.23) можно вычислить и 0 g g 983,2 см / с2 , а на экваторе / 2 g g 2 R 981,2 см / с2 . Очевидно, разность значений g на полюсе и экваторе обусловлена сплюснутостью Земли. Экватор на экваторе – дальше отстоит от центра Земли, чем полюсы, поэтому тела на экваторе притягиваются к центру слабее, чем на полюсе. Рис. 15.7 а Рис. 15.7 б Если тело движется относительно Земли, то в игру вступает и кориолисова сила инерции, которая приводит к следующим эффектам (рис.15.7а). При движении по меридиану к полюсам она смещает тела вправо по ходу их движения, т.е. на восток - в северном полушарии, и на запад – в южном. Этим объясняется изношенность правых берегов рек (Объ, Енисей, Лена), впадающих в Северный ледовитый океан. Заметьте, при пересечении экватора по меридиану, сила Кориолиса меняет свой знак. Например, пассаты – ветры, дующие по меридиану от тропиков к экватору от обоих полушарий, под действием кориолисовой силы отклоняются к западу. При движении по параллелям на восток (на запад) кориолисова сила действует на тело в сторону экватора (соответствующего полюса) и вертикально вверх (вниз). Причем эти составляющие силы Кориолиса зависят от географической широты: чем ближе параллель к экватору, тем больше вертикальная сила. В частности, при движении по экватору сила Кориолиса направлена вертикально: вверх – при движении на восток, и вниз – при движении на запад. При движении тела в вертикальном направлении сила Кориолиса направлена по параллели (на восток, или на запад). В частности, свободно падающее тело без начальной скорости отклоняется от направления отвеса в основном к востоку (рис.15.7 б), и намного меньше к экватору. Это объясняется тем, что на падающее (без начальной скорости) тело сила Кориолиса направлена на восток, которая в этом направлении сообщает телу небольшую составляющую скорости. Кориолисов сила, действуя на эту составляющую скорости, смещает тело к экватору. Причем, если смещение на восток имеет порядок величины Ω, то смещение на экватор – порядка 2 , которое из-за малости, обычно недоступно наблюдению. Например, при падении тела с высоo ты 200м, для широты Еревана ( 42 ) получаем смещение на восток 2,4 см, в то время как смещение к экватору составляет лишь 0.7 мм. Рис. 15.8 С силой Кориолиса связано поведение маятника Фуко, явившееся первым доказательством вращения Земли вокруг своей оси. В отсутствие силы Кориолиса плоскость колебаний маятника оставалась бы неизменной, так как сила тяжести и натяжения нити лежат в этой плоскости. Дей- ствие этой силы, направленной перпендикулярно плоскости колебаний (рис.15.8), вращает эту плоскость вокруг вертикального направления с угловой скоростью sin , где – угловая скорость вращения Земли, – широта места подвеса маятника. В частности, на полюсе плоскость колебаний совершает полный оборот за сутки, а на экваторе этот эффект отсутствует. Инертная и гравитационная массы. Принцип эквивалентности. Понятие массы мы ввели с целью количественной характеристики свойства инертности тел. Это инертная масса, которая входит в выражение второго закона Ньютона: mин a F . Однако тела обладают также свойством притягивать другие тела силой гравитации, т.е. обладают, можно сказать, гравитационным «зарядом», который называется гравитационной массой. Эта масса входит в выражение закона всемирного тяготения: F m1гр m2гр . r2 Оказывается, что во сколько раз увеличивают инертные свойства тела, во столько же раз растет свойство его гравитационного притяжения, т.е. инертная и гравитационная масса тела пропорциональны друг друга. Это есть обобщение опытов и является физическим законом эквивалентности инертной и гравитационной масс. Поэтому, если коэффициент пропорциональности в формуле закона всемирного тяготения выбирать таким образом ин G , чтобы mгр из- гр мерялась в единицах инертной массы, т.е. если m и m данного тела измерять в одних и тех же единицах, то их численные значения также совпадут. Например, опыты Галилея, установившие независимость ускорения свободного падения от массы тела, являются первым доказательством принципа эквивалентности. Действительно, тело у поверхности Земли притягивается силой тяжести: M mгр F G mгр g , 2 R которая, согласно второго закона Ньютона сообщает телу ускорение F mгр a ин ин g. m m Так как для всех тел a g, то отсюда следует равенство инертной и гравитационной масс. В настоящее время равенство этих масс экспериментально установлено с точностью 1012 . рис. 15.9 Из равенства инертной и гравитационной масс следует эквивалентность сил инерции и гравитации. Действительно, рассмотрим по примеру Эйнштейна, два лифта – один, покоящийся у поверхности Земли, а другой - вдали от гравитирующих тел, которому тянут за трос с ускорением тела a g в (рис.15.9). Тела в лифте подвергаются действию земного притяжения ускоренно Fгр m a m g . гр гр движущемся лифте – действию поступательной Fин mин g , а силы инерции Так как инертная и гравитационная массы не отличаются друг от друга, то неотличимы и силы инерции и гравитации Fин и Fгр . Поэтому все физические процессы в обоих лифтах будут протекать одинаковым образом. Следует учесть, что эквивалентность сил инерции и гравитации имеет место лишь в небольших объемах пространства, где гравитационное поле можно считать однородной. Контрольные вопросы: Укажите несколько неинерциальных систем отсчета. Как преобразуется скорость при переходе от ИСО к НСО? Как преобразуется ускорение при переходе от ИСО к НСО? Как обобщается понятие силы в НСО? Какие силы действуют на частицу в НСО? Каковы особенности сил инерции? Опишите действия поступательной, центробежной, кориолисовой сил инерции. Каково уравнение движение в Геоцентрической СО? Какие вы знаете эффекты сил инерции на движения частиц в приземной области? Каково поведение маятника Фуко? Что характеризуют инертное и гравитационные массы? В чем заключается принцип эквивалентности?