Проектирование информационной образовательной

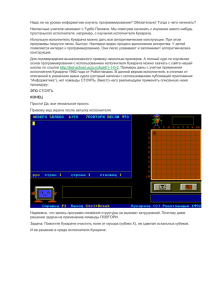
Проектирование информационной образовательной среды
«Треугольник»
Соседко Елена Викторовна,
учитель информатики муниципального бюджетного общеобразовательного
учреждения «Средняя общеобразовательная школа №8»
Существует целый ряд авторских трактовок, определяющих специфику
обучающей среды, основанной на компьютерных технологиях, но цель у них
одна - интеграция информационных и телекоммуникационных технологий в
образовательный процесс.
В Интернете за десятки лет накопилось много методических
материалов на русском языке для многих дисциплин. Но творческого учителя
в любом материале что-нибудь да не устраивает, хочется изменить или не
нравится, что порой невозможно по программно-техническим причинам.
Если есть время и определенные знания, то можно создавать
собственное программное обеспечение, например, в среде программирования
Lazarus. Этот программный продукт является свободно распространяемым,
и существуют его дистрибутивы как для Linux, так и для Windows.
Например, учителю математики можно разработать интерактивную
динамическую информационную образовательную среду по теме
«Треугольник».
Во-первых, нужно собрать информацию, связанную с понятием
«треугольник»: условия существования, вершины, стороны, классификация
по углам, классификация по сторонам, измерения углов, длины сторон,
периметр, площадь, высота, вписанная окружность и т.д.
Во-вторых, структурировать эту информацию.
Вершины: координаты: Стороны: длина. Условия существования: три
вершины не лежат на одной прямой, сумма длин любых двух сторон больше
третьей стороны. Классификация по углам: прямоугольный, остроугольный,
тупоугольный. Классификация по сторонам: неравносторонний,
равнобедренный, равносторонний. Углы: градусы, радианы. Периметр:
формула, значение. Площадь: формула, значение. Медиана: уравнение,
длина. Высота: уравнение, длина. Биссектриса: уравнение, длина.
Вписанная окружность: координаты центра, радиус. Описанная окружность:
координаты центра, радиус.
В-третьих, описать необходимые первичные переменные (табл.1).
Таблица 1
Описание первичных переменных
Абсцисса вершины А
Ax
Ордината вершины А
Ау
Абсцисса вершины В
Bx
Ордината вершины В
Bу
Абсцисса вершины С
Cx
Ордината вершины С
Сy
периметр
Pt
полупериметр
pp
площадь
St
Длина стороны АВ
dAB
Длина стороны АС
dAC
Длина стороны ВС
dBC
Угол ВАС
uA
Угол АСB
uC
Угол АBС
uB
В-четвёртых, провести следующие действия.
1. Открыть среду программирования Lazarus (Delphi).
2. Создать новое приложение (Файл «Создать Проект Приложение»).
3. Придать форме Form1 квадратную форму размером не менее четверти
экрана (рис.1).
4. Добавить на форму кнопку Button1 и изменить надпись на «Построить и
вычислить» (свойство Caption в инспекторе объектов)
5. Добавить на форму графическое поле Image для построений, для
координат вершин шесть объектов Label и Edit, необходимое количество
CheckBox для отбора вычислений, нужное количество StaticText для вывода
результатов.
Рис. 1
6. На кнопке Button1 создать обработчик событий (двойной щелчок на
кнопке) и вписать текст программы (рис.2).
procedure TForm1.Button1Click(Sender: TObject);
var mx,my:integer;
begin
masht:=20;
Ax:=strtofloat(Form1.Edit1.Text); Ay:=strtofloat(Form1.Edit2.Text);
Bx:=strtofloat(Form1.Edit3.Text); By:=strtofloat(Form1.Edit4.Text);
Cx:=strtofloat(Form1.Edit5.Text); Cy:=strtofloat(Form1.Edit6.Text);
dAB:=sqrt(sqr(Bx-Ax)+sqr(By-Ay));
dAC:=sqrt(sqr(Cx-Ax)+sqr(Cy-Ay));
dBC:=sqrt(sqr(Cx-Bx)+sqr(Cy-By));
pt:=dAB+dBC+dAC;
pp:=pt/2;
St:=sqrt(pp*(pp-dAB)*(pp-dAC)*(pp-dBC));
mx:=Image1.Width;my:=Image1.Height; Image1.Canvas.Brush.color:=clwhite;
Image1.Canvas.FillRect(0,0,mx,my);
Image1.Canvas.Brush.color:=clblack;
Image1.Canvas.pen.color:=clgray;
Image1.Canvas.pen.width:=1;
Image1.Canvas.Line(0,my div 2,mx,my div 2);
Image1.Canvas.Line(mx div 2,my,mx div 2,0);
Image1.Canvas.pen.color:=clblack;
Image1.Canvas.pen.width:=2;
Image1.Canvas.Polyline([Point(mx div 2 +round(masht*Ax),my div 2-round(masht*Ay)),
Point(mx div 2+round(masht*Bx),my div 2-round(masht*By)),
Point(mx div 2+round(masht*Cx),my div 2-round(masht*Cy)),
Point(mx div 2 +round(masht*Ax),my div 2-round(masht*Ay))]);
if Form1.Checkbox2.Checked
then Form1.StaticText1.Caption:='S='+floattostr(St)
else Form1.StaticText1.Caption:='' ;
if Form1.Checkbox1.Checked
then
Form1.StaticText2.Caption:='p='+floattostr(Pt) else
Form1.StaticText2.Caption:='';
if Form1.Checkbox3.Checked
then
Form1.StaticText4.Caption:='AB='+floattostr(dAB) else
Form1.StaticText4.Caption:='';
if (dAB<>dAC)and(dBC<>dAB)and(dBC<>dAC)
then
Form1.StaticText3.Caption:='треугольник неравносторонний';
if (dAB=dAC)and(dBC=dAB)and(dBC=dAC)
then
Form1.StaticText3.Caption:='треугольник равносторонний' else
if (dAB=dAC)or(dBC=dAB)or(dBC=dAC)
then
Form1.StaticText3.Caption:='треугольник равнобедренный';
uA:=arccos((dBC*dBC-dAC*dAC-dAB*dAB)/(-2*dAC*dAB));
if Form1.Checkbox6.Checked
then
Form1.StaticText7.Caption:='A='+floattostr(uA) else
Form1.StaticText7.Caption:='';
end;
Рис.2
7. Дополнить глобальный раздел var переменными masht:integer;
Ax,Ay,Bx,By,Cx,Cy,St,pt,pp,dAB,dAC, dBC,uA:real; и дополнить список
модулей словом Math.
8. Запустить проект на выполнение (напр. нажать F9).
9. В открывшемся окне откомпилированного приложения активировать
кнопку «Построить и вычислить».
10. Закрыть окно запуска. Сохранить проект в отдельной папке.
(Чтобы вращение не было конечным, а завершилось по определенному
действию пользователя, надо внести некоторые изменения в проект.)
11.Вставить комментарии, поясняющие роль каждого фрагмента
программы (рис.3).
Рис.3
Программа может быть дополнена любыми функциями, необходимыми
учителю математики в зависимости от тематики: простой треугольник, метод
координат и т.п.
Литература
1.
Семенцова, О. В. Создание информационно-образовательной среды
школы. [Электронный ресурс]
http://festival.1september.ru/articles/513446 (Дата обращения: 12.12.2013).
2.
Понятие информационно-образовательной среды ОУ - материалы к
дистанционному курсу - часть 1. [Электронный ресурс]
http://www.openclass.ru/node/21749 (Дата обращения: 12.12.2013).
3.
Как нарисовать треугольник. [Электронный ресурс]
http://www.cyberforum.ru/lazarus/thread846579.html (Дата обращения:
12.12.2013).
4.
Скорнякова, Т. Е. Решение треугольника. [Электронный ресурс]
http://tskorni.jimdo.com/lazarus%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1
%8C%D0%BD%D0%B8%D0%BA%D0%B0/ (Дата обращения:
12.12.2013).