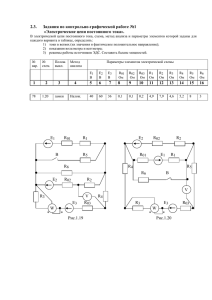
M и M и k Q , M .

ХИМИЯ
336
УДК 517.977.5
РЕШЕНИЕ ПРЯМОЙ И ОБРАТНОЙ КИНЕТИЧЕСКИХ ЗАДАЧ ДЛЯ ПРОЦЕССА
ЭМУЛЬСИОННОЙ СОПОЛИМЕРИЗАЦИИ БУТАДИЕНА СО СТИРОЛОМ
© Э. Н. Мифтахов1*, И. Ш. Насыров2, С. А. Мустафина1, С. И. Спивак3
1
Стерлитамакская государственная педагогическая академия им. З. Биишевой
Россия, Республика Башкортостан, 453103 г. Стерлитамак, пр. Ленина, 49.
Тел./факс: +7 (3473) 43 10 39.
2
ОАО «Синтез-Каучук»
Россия, Республика Башкортостан, 453110 г. Стерлитамак, ул. Техническая, 14.
Тел./факс: +7 (3473) 20 40 09.
3
Башкирский государственный университет
Россия, Республика Башкортостан, 450074 г. Уфа, ул. Заки Валиди, 32.
Тел./факс: +7 (347) 229 96 35.
E-mail: [email protected]
Построена математическая модель процесса эмульсионной сополимеризации бутадиена со
стиролом. Решена прямая кинетическая задача для расчета характеристик молекулярномассового распределения. При моделировании использован метод моментов в сочетании с методом
производящих функций. Решена обратная задача путем аппроксимации конверсионной зависимости и найдены кинетические константы скоростей реакций рекомбинации и диспропорционирования. Проведен сравнительный анализ экспериментальных и расчетных значений характеристической вязкости, среднечисленных и среднемассовых молекулярных масс от времени. Результаты
расчетов показывают удовлетворительное согласование с экспериментальными данными.
Ключевые слова: сополимеризация, бутадиен, стирол, кинетика, обратная задача, молекулярномассовое распределение.
Производство полимерных материалов занимает одно из ведущих мест в современной химической промышленности. Многие полимерные продукты получают методом радикальной сополимеризации, когда исходными соединениями являются
несколько (2 и более) мономеров. В частности, этот
механизм лежит в основе технологии производства
эмульсионного бутадиен-стирольного каучука.
Процесс сополимеризации бутадиена со стиролом в производстве синтетического каучука проводится непрерывным способом в батарее последовательно соединенных между собой полимеризаторов
при температуре 5 ºС [1]. Для регулирования молекулярной массы применяется трет-додецилмеркаптан.
Процесс сополимеризации останавливают при конверсии мономеров 70%.
Кинетический метод моделирования полимеризационных процессов заключается в составлении и
численном решении кинетических уравнений для
концентрации всех типов частиц, участвующих в
процессе. При построении модели сополимеризации
бутадиена со стиролом в эмульсии будем считать, что
реакционная способность активного центра на конце
растущей цепи определяется лишь природой концевого звена [2]. Рассмотрим по четыре элементарных
реакции роста и обрыва цепи с участием двух мономеров M 1 и M 2 и двух типов растущих цепей, отличающихся природой концевого звена. Тогда кинетическую схему сополимеризации бутадиена со стиролом можно описать в виде следующих стадий:
1. Инициирование. На стадии инициирования образуются свободные радикалы. Их образование происходит в два этапа. На первом этапе распадаются молекулы инициатора (I), содержащиеся в исходной смеси:
k
I →
R,
d
где
kd
– константа скорости распада инициатора,
R – инициирующий (первичный) радикал. Заме-
* автор, ответственный за переписку
тим, что в литературе часто встречается запись, где
в результате распада инициатора происходит образование не одного, а двух свободных радикалов
(2R). Однако здесь мы несколько упрощаем вид
стадии, а саму константу скорости распада инициатора рассчитываем из результатов его исчерпывания в ходе процесса.
На втором этапе инициирования в результате
взаимодействия первичного радикала и мономеров
M 1 и M 2 образуются мономерные радикалы, отличающиеся природой концевого звена:
k
R + M 1 →
P11, 0 ,
i1
k
R + M 2 →
P02,1 ,
i2
где ki – константа скорости реакции инициирования.
2. Рост цепи:
Pn1,m + M 1 → Pn1+1,m ,
k p 11
Pn1,m + M 2 → Pn2,m +1 ,
k p 12
Pn2,m + M 1 k→ Pn1+1,m ,
p 21
Pn2,m + M 2 → Pn2,m +1 ,
k p 22
где kp – константа скорости реакции роста цепи,
Pn ,m – активная («растущая») цепь сополимера дли-
ной n + m , содержащая n звеньев мономера M 1 и
m звеньев мономера M 2 .
3. Передача цепи в результате взаимодействия с регулятором S :
Pn1,m + S →
 Qn ,m + R,
k reg 1
Pn2,m + S →
 Qn ,m + R,
k reg 2
где k reg – константа скорости реакции передачи
цепи, Qn ,m – неактивная («мертвая») цепь сополи-
мера длиной n + m , содержащая n звеньев мономера M 1 и m звеньев мономера M 2 .
Вестник Башкирского университета. 2011. Т. 16. №2
ISSN 1998-4812
и неактивных цепей:
4. Обрыв цепи в результате рекомбинации:
1
n ,m
P
+∞ +∞
+ P → Qn + r ,m+ q ,
1
r ,q
ψ kQ = ∑ ∑ (nwa + mwb ) k Qn ,m ,
k r 11
n =0 m =0
k
Pn1,m + Pr2,q →
Qn +r ,m + q ,
r 12
где k = 0,1,K, ∞ .
Перепишем систему (1) в виде:
(k M + k M + k S + (k + k )C + (k + k )C )P
k
Pn1,m + Pr1,q →
Qn + r ,m+ q ,
r 21
1
n ,m
P
1
+ P → Qn + r ,m + q ,
1
r ,q
P
+ P → Qn ,m + Qr ,q ,
2
n,m
+ P → Qn ,m + Qr ,q ,
P
+ k p 21 M P
1
2
n −1, m
2
k p 22 M 2 Pn2,m + k p 21M 1 Pn2,m − k p12 M 2 Pn1,m−1 − k p 22 M 2 Pn2,m−1 + k reg 2 SPn2,m +
+ k r 22C M P
2
2
n ,m
+ k r 21C M P
1
2
n ,m
+ k d 22C M P
2
2
n ,m
+ k d 21C M P
2
n ,m
1
1
CM =
2
∞
∑P
n ,m =0
∞
1
n ,m
2
n ,m
n ,m =0
F ( s, u ) = ∑∑ s n +m u nw + mw Pn2,m .
a
ψ
+∞ +∞
Домножив левую и правую части (3) на
s n + m u nw + mw
a
b
и просуммировав получившиеся
выражения по n, m , получим линейную систему
уравнений относительно G ( s, u ) и F ( s, u ) :
(k
(k
(k
(k
p11
M 1 + k p12 M 2 + k reg1 S + (k r11 + k d 11 )C M + (k r12 + k d 12 )C M )G =
= ∑∑ (nwa + mwb ) P ,
n =0 m = 0
+∞ +∞
ψ kM = ∑∑ (nwa + mwb ) k Pn2,m ,
2
n =0 m =0
2
a
p 22
M 2 + k p 21 M 1 + k reg 2 S + (k r 21 + k d 21 )C M + (k r 22 + k d 22 )C M )F =
1
M 1G + k p 22 M 2 F + Q1, 0 )su w ,
(5 )
2
b
p12
Выражая G ( s, u ) и F ( s, u ) из системы (5), получим формулы для расчета моментов молекулярно-массового распределения (ММР) активных цепей сополимера [4]:
ψ kM =
= 0,
1
n ,m
1
M 1G + k p12 M 2 F + P1, 0 )su w ,
p11
d k G ( s, u )
s = u = 1,
du k
(6 )
k
d F ( s, u )
s = u = 1,
du k
где ψ kM ,ψ kM – моменты k -го порядка активных
цепей сополимера, отличающихся природой концевого звена; wa , wb – молекулярная масса мономе1
2
ров M 1 и M 2 соответственно.
Для расчета средних молекулярных масс сополимера необходимо знание моментов до 2-го
порядка включительно, тогда система дифференциальных уравнений относительно моментов ММР
сополимера примет вид:
dI
= −k i I ,
dt
dM 1
= −k p11 M 1C M − k p 21 M 1C M ,
dt
dM 2
(7)
= −k p12 M 2 C M − k p 22 M 2C M ,
dt
dS
= − k reg1 SC M − k reg 2 SC M ,
dt
dψ αQ
= Aα k r , k d , k reg ,ψ βM ,ψ βM , [S ], [I ], [M 1 ], [M 2 ], C , C .
dt Моменты же активных цепей M M 1 ,M
M2
1
2
1
2
1
k
b
n =0 m =0
2
.
(4 )
+∞ +∞
ψ kM =
,
b
n=0 m =0
(1 )
Принципиальное отличие полимеризационных
процессов от всех других химических процессов
состоит в том, что вместо продукта с фиксированной молекулярной массой получают некоторое молекулярно-массовое распределение полимера (ММР).
Статическая теория полимеризации исходит из
возможности анализа ММР по особого рода средним молекулярным массам M w , M n , называемых
среднемассовой и среднечисленной. Для анализа
вводятся понятия моментов активных цепей:
M1
k
(3 )
2
a
(2)
∑P
=
+∞ +∞
где C 1 и C 2 – концентрации активных цепей,
M
M
отличающиеся природой концевого звена:
CM =
1
n ,m
M2
,
1
1
d 12
1
k p11M 1 Pn1,m + k p12 M 2 Pn1,m − k p11 M 1 Pn1−1,m − k p 21 M 1 Pn2−1,m + k reg1 SPn1,m +
2
r 12
G ( s, u ) = ∑∑ s n + m u nw + mw Pn1,m ,
где k r , k d – константы скоростей реакций рекомбинации и диспропорционирования.
Составляя матрицу стехиометрических коэффициентов и умножая ее на вектор-столбец скоростей реакции, получим бесконечную (порядка 106 )
систему нелинейных дифференциальных уравнений, описывающую процесс сополимеризации бутадиена со стиролом.
Упростим систему за счет использования
принципа квазистационарности [3], заключающегося в постоянстве концентраций активных цепей.
Тогда скорость образования радикалов (активных
цепей) на стадии инициирования равна скорости их
гибели на стадии обрыва:
dPn1,m
dP 2
= 0, n ,m = 0.
dt
dt
Относительно Pn1,m и Pn2,m получим:
1
M1
M 2 + k p 21 M 1 + k reg 2 S + (k r 21 + k d 21 )C M + (k r 22 + k d 22 )C M )Pn2,m =
p 22
k d 22
+ k r11C M Pn1,m + k r 12C M Pn1,m + k d 11C M Pn1,m + k d 12C M Pn1,m = 0,
d 11
Получившуюся систему уравнений (3) решим
с использованием производящих функций вида:
k d 21
2
r ,q
r 11
n, m > 1.
d 12
P
reg 1
k p12 M 2 Pn1,m−1 + k p 22 M 2 Pn2, m−1 ,
Pn1,m + Pr2,q k→ Qn ,m + Qr ,q ,
1
r ,q
1
n −1, m
k p11 M P
(k
k d 11
2
n,m
p12
1
+ P → Qn ,m + Qr ,q ,
1
r ,q
2
p11
k r 22
и диспропорционирования:
1
n ,m
337
(
2
1
2
1
ψα
( α = 0,1,2 ) рассчитываются по формулам (6).
2
)
ψα
ХИМИЯ
338
Начальные условия для системы (7) имеет вид:
I (0) = I 0 , M 1 (0) = M 01 , M 2 (0) = M 02 , S (0) = S 0 , (8)
ψ sQ (0) = ψ sM (0) = ψ sM (0) = 0, β = 0,1,2.
1
2
Найденные значения молекулярно-массового
распределения сополимера подставим в формулы
для нахождения среднечисленной ( M nQ ) и средне-
характеристической вязкости, вычисленной по
формуле (10), удовлетворительно описывают данные результатов эксперимента, проведенного в
центральной заводской лаборатории ОАО «СинтезКаучук» (г. Стерлитамак), что подтверждает адекватность используемой нами модели.
массовой ( M wQ ) молекулярных масс:
ψ 1Q
,
ψ 0Q
ψQ
M wQ = 2Q .
ψ1
M nQ =
(9 )
Не менее важным показателем качества продукта сополимеризации является значение характеристической вязкости [η ], для расчета которой будем использовать зависимость, описанную в работе [5]:
(10)
[η ] = 5.4 × 10 −4 M ηQ 0.66 .
Кинетические параметры сополимеризации
бутадиена со стиролом в эмульсии (при 5 °C) были
взяты из работы [6], однако не все найденные значения соответствуют условиям и механизму процесса эмульсионной сополимеризации. Потому для
уточнения некоторых кинетических параметров
(констант скоростей реакций рекомбинации и диспропорционирования) проводится решение обратной задачи путем аппроксимации конверсионной
зависимости.
Стратегия поиска кинетических параметров
сополимеризации заключается в поиске минимума
функции соответствия (11) экспериментально определяемых параметров и вычисленных на основе
математической модели, описывающей процесс
сополимеризации (7)–(8):
p
2 r
H ( z ) = ∑ (K iэксп. − K iрасч. ) , z = (k d , k r ),
(11)
i =1
. – значения конверсии, определенные в
где K эксп
j
ходе эксперимента, K jрасч. – расчетные значения
конверсии, определяемые по формуле:
F M + F jM
K jрасч. = 1 − j 1
,
M +M2
M
M
где F j и Fj – значения концентрация мономеров
1
2
2
1
Рис. Зависимость экспериментальных (точки) и расчетных (сплошная линия) значений характеристической
вязкости (а), среднечисленных (б) и среднемассовых (в)
молекулярных масс от времени.
M1 и M 2:
F jM = M 1 ⋅ exp((− k p11 ⋅ C M − k pr 22 ⋅ C M / r2 ) ⋅ t j ),
ЛИТЕРАТУРА
1
1
F
M2
j
2
= M ⋅ exp((− k p11 ⋅ C M / r1 − k p 22 ⋅ C M ) ⋅ t j ).
1.
2
1
2
Для уточнения кинетических параметров путем минимизации функционала (11) использовался
метод Хука–Дживса.
Применяя неявный метод Адамса–Мултона 4го порядка для численного решения жесткой системы дифференциальных уравнений (7)–(8) и подставляя значения моментов в (9)–(10), определим
Q
зависимости M wQ , M n и [η ] от времени сополимеризации (рис.). Из приведенных зависимостей видно, что значения усредненных молекулярных масс,
вычисленных по формулам (9), а также значение
2.
3.
4.
5.
6.
Кирпичников П. А., Береснев В. В., Попова Л. М. Альбом
технологических схем основных производств промышленности синтетического каучука. Л.: Химия, 1986. 224 с.
Семчиков Ю. Д. Высокомолекулярные соединения. М.:
Академия, 2003. 368 с.
Подвальный С. Л. Моделирование промышленных процессов полимеризации. М.: Химия, 1979. 256 с.
Ray W. H., Douglas T. I., Godsalve E. W. Molecular weight
distribution in copolymer systems. II. Free radical copolymerization // Macromolecules. 1971. V. 4. P. 166–174.
Booth C., Beason L. R., Bailey J. T. Incremental Modification
of styrene-butadiene rubber with tert-dodecyl mercaptan //
J. Appl. Polymer Sci. 1961. V. 13. P. 116–123.
Brandrup J., Immergut E. H., Grulke E. A. Polymer Handbook.
Wiley, 1998. 2317 p.
Поступила в редакцию 19.01.2011 г.
После доработки – 10.05.2011 г.