3 Лекция 10. ИЗОБРАЖЕНИЕ ПЛОСКИХ ДЕФЕКТОВ

Лекция 10.
ИЗОБРАЖЕНИЕ ПЛОСКИХ ДЕФЕКТОВ
Трансляционный контраст. Матрица рассеяния. Дефекты упаковки в гцк материалах. πи δ- контуры. Границы фаз. Поля упругих напряжений. Контраст от одиночной
дислокации. Дислокационные петли и диполи. Изображение в моде слабый-пучок
темное-поле (WBDF).
ИЗОБРАЖЕНИЕ ПЛОСКИХ ДЕФЕКТОВ.
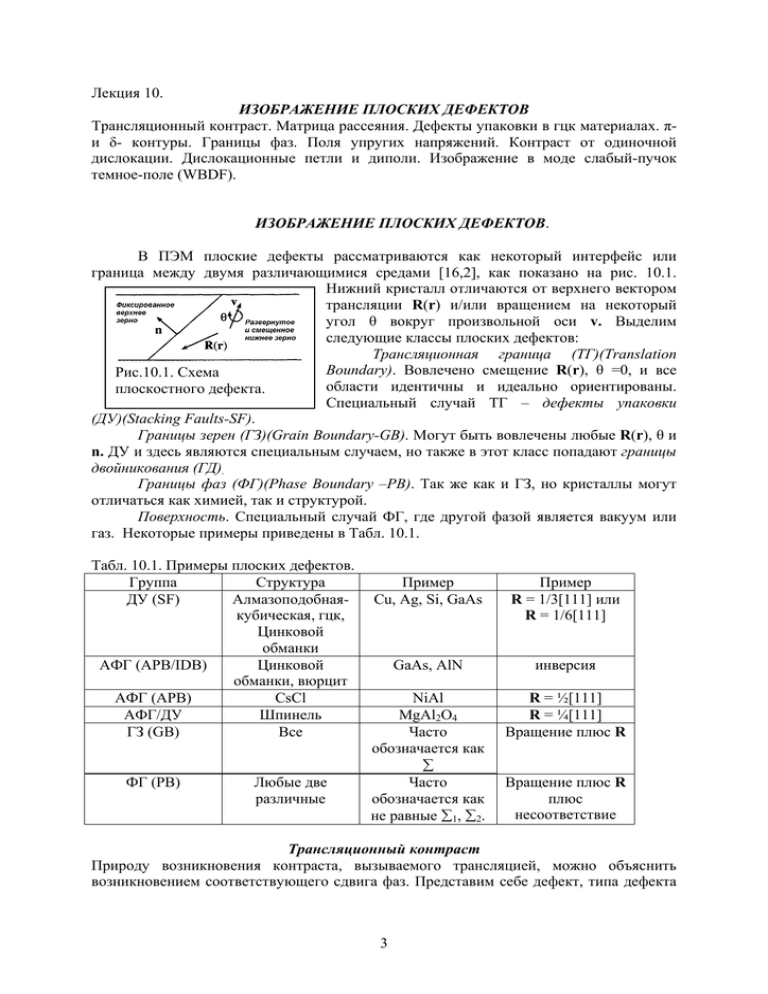
В ПЭМ плоские дефекты рассматриваются как некоторый интерфейс или
граница между двумя различающимися средами [16,2], как показано на рис. 10.1.
Нижний кристалл отличаются от верхнего вектором
трансляции R(r) и/или вращением на некоторый
угол θ вокруг произвольной оси v. Выделим
следующие классы плоских дефектов:
Трансляционная граница (ТГ)(Translation
Boundary). Вовлечено смещение R(r), θ =0, и все
Рис.10.1. Схема
области идентичны и идеально ориентированы.
плоскостного дефекта.
Специальный случай ТГ – дефекты упаковки
(ДУ)(Stacking Faults-SF).
Границы зерен (ГЗ)(Grain Boundary-GB). Могут быть вовлечены любые R(r), θ и
n. ДУ и здесь являются специальным случаем, но также в этот класс попадают границы
двойникования (ГД).
Границы фаз (ФГ)(Phase Boundary –PB). Так же как и ГЗ, но кристаллы могут
отличаться как химией, так и структурой.
Поверхность. Специальный случай ФГ, где другой фазой является вакуум или
газ. Некоторые примеры приведены в Табл. 10.1.
Табл. 10.1. Примеры плоских дефектов.
Группа
Структура
ДУ (SF)
Алмазоподобнаякубическая, гцк,
Цинковой
обманки
АФГ (APB/IDB)
Цинковой
обманки, вюрцит
АФГ (APB)
CsCl
АФГ/ДУ
Шпинель
ГЗ (GB)
Все
ФГ (PB)
Любые две
различные
Пример
Cu, Ag, Si, GaAs
Пример
R = 1/3[111] или
R = 1/6[111]
GaAs, AlN
инверсия
NiAl
MgAl2O4
Часто
обозначается как
∑
Часто
обозначается как
не равные ∑1, ∑2.
R = ½[111]
R = ¼[111]
Вращение плюс R
Вращение плюс R
плюс
несоответствие
Трансляционный контраст
Природу возникновения контраста, вызываемого трансляцией, можно объяснить
возникновением соответствующего сдвига фаз. Представим себе дефект, типа дефекта
3
упаковки, где ячейки нижнего кристалла, отделенного от верхнего плоскостью,
смещены на некоторую величину R, так что координаты ячеек равны
r'n = rn + R.
(10.1)
Фаза в экспоненциальном члене exp(-2πiKr) в (7.7) будет определятся Kr’n
Kr’n = (g + s)·(rn + R) = g·rn + g· R + s· rn + s·R
(10.2)
С учетом свойств произведения векторов прямой и обратной решеток (6.9), и в
предположении малости векторов s и R, имеем модифицированные уравнения ХовиУэлана (7.11):
d φg/dz = (πi/ξ0)φg + (πi/ξg)φ0 exp[-2πi(sz+gR)]
(10.3а)
d φ0/dz = (πi/ξ0)φ0 + (πi/ξg)φg exp[2πi(sz+gR)].
(10.3б)
Делая замену переменных (7.13)
φ0s = φ0exp(-πiz/ξ0)
(10.4а)
(10.4б)
φgs = φgexp(2πisz -πiz/ξ0),
Получаем
dφ0s/dz = (πi/ξg)φgs exp(-2πigR)
(10.5а)
dφgs/dz = (2πis/ξ0)φgsexp(-2πigR) + (πi/ξg)φ0s.
(10.5б)
Таким образом, присутствие дефекта приводит к появлению дополнительного члена
exp(-2πigR) в дифрагированной волне и дефект может быть виден, если
дополнительный сдвиг фаз не равен нулю:
α = 2πigR ≠ 0
(10.6)
Матрица рассеяния
Решения уравнений Хови-Уэлана удобно
представить в виде матрицы рассеяния. Воспользуемся
подходом, развитым Хиршем и др. [16] Представим
себе плоский дефект, для простоты, параллельный
поверхности и расположенный на глубине t1 от верхней
поверхности, как изображено на рис. 10.2. В Л7 мы
показали, что решения уравнения Хови-Уэлана можно
Рис.10.2. Схема
представить в виде (7.15, 7.17б)
расположения дефекта
(10.7а)
φ0 = С0exp(2πiγz)
упаковки.
φg = С gexp(2πiγz).
(10.7б)
Поскольку имеются два решения уравнения (7.16) для
γ, то в 2-х-пучковом приближении обе, 0- и g- амплитуды, должны быть комбинациями
типа
(10.8а)
φ0 = С01ψ1exp(2πiγ1z)+С02ψ2exp(2πiγ2z)
φg = Сg1ψ1exp(2πiγ1z)+Сg2ψ2exp(2πiγ2z),
(10.8б)
где ψ1 и ψ2 отражают относительный вес γ1 и γ2 членов. Это можно переписать в
матричном виде
С01 С02
ψ1
φ0 (z)
exp(2πiγ1z) 0
=
·
·
(10.9)
Сg1 Сg2
ψ2
φg (z)
0
exp(2πiγ2z)
На границе матрица с exp равна единичной, и, соответственно,
φ0 (0)
φg (0)
=
С
·
ψ1
ψ2
(10.10)
где С –матрица из С0 и Cg, как видно из сопоставления (10.9) и (10.10).
Или
4
ψ1
ψ2
=
С-1
·
φ0 (0)
φg (0)
(10.11)
где С-1 – матрица, обратная С-матрице в (10.10), т.е. С-1С = I – единичной матрице.
Поэтому, (10.9) можно переписать в виде
φ0 (z)
exp(2πiγ1z) 0
φ0 (0)
=
С ·
· С-1·
(10.12)
φg (z)
0
exp(2πiγ2z)
φg (0)
Или
φ0 (z)
φ (0)
= P(z) 0
(10.13)
φg (z)
φg (0)
где P(z) – матрица рассеяния или матрица-пропагатор:
или
exp(2πiγ1z) 0
P(z)
=
С ·
· С-1,
(10.14)
0
exp(2πiγ2z)
(10.15)
P(z) = C ГС-1,
где Г – фазовая матрица, содержащая зависимость от глубины z.
Решение задачи определения результирующей амплитуды для задачи с
дефектами сводится к послойному определению эволюции амплитуд. В частности для
дефекта, схематично изображенного на рис. 10.2, образец состоит из двух слоев. Волны
φ0 (t1) и φg (t2), выходящие из верхнего слоя, являются входными волнами для нижнего
слоя. При этом, эффект трансляции R приводит к появлению дополнительного
фазового множителя exp(-iα) перед Сg, где α = 2πgR (10.5,6). Т.о., обозначив С –
матрицу в (10.10) в первом слое С1, матрицу С2 во втором слое получаем в виде
С01
С02
(10.16)
Сg1 exp(-iα) Сg2 exp(-iα)
Тогда на выходе имеем результирующие амплитуды
φ0 (t)
φ (0)
= P( t2) · P(t1) 0
(10.17)
φg (t)
φg (0)
Это уравнение используется в компьютерных расчетах контраста по слоевой модели.
При соответствующем выборе координат С-матрица становится унитарной, и,
опуская фазовый фактор, амплитуды могут быть выражены в следующем виде [16]:
φ0 (t) = [cos(π∆kt) – icos(β)sin(π∆kt)] + ½[(exp(iα)-1]sin2βcos(π∆kt)
(10.18а)
– ½ [exp(iα)-1]sin2βcos(2π∆kt’)
φg (t) = isinβsin(π∆kt) + ½ sinβ[1- exp(-iα)] [cosβcos(π∆kt)-i sin(π∆kt)]
- ½ sinβ[1- exp(-iα)] [cosβcos(2π∆kt’)-i sin(2π∆kt’)]
(10.18б)
В правой части (10.18) 1-й член соответствует R=0, 2-й член не зависит от положения
дефекта и 3-й член осциллирует с периодичностью 1/∆k, т.е. амплитуды показывают ту
же самую зависимость от толщины и ξeff, что и без дефекта.
С2
=
Рис.10.3 Геометрия ДУ.
Дефекты упаковки в гцк материалах
Гцк решетки наиболее распространены в чистых
материалах, особенно среди металлов, а также среди
многих компаундов. Трансляции в гцк материалах
хорошо известны, они прямо соотносятся с
параметром решетки: R= 1/6 <-1-12> или 1/3<111>,
которые отличаются на вектор ½ <110> (т.н.
частичные или парциальные дислокации Шокли).
5
Наиболее часто встречающаяся и удобная для исследования геометрия образца
изображена на рис. 10.3. Если ось [111] совпадает с нормалью к поверхности, то
дефекты будут располагаться на плоскости либо параллельной поверхности, либо
расположенной на другой плоскости скольжения, например (11-1). В последнем случае
R=± 1/3[11-1] и фазовый фактор α = 2πgR = 0, если g = (2-20). Т.е. в DF от g = (2-20)
дефект не будет давать контраст. Необходимо использовать для наблюдения дефекта
другое g, например, g = (02-2), тогда gR= 4/3 или -4/3 и α = ±1200. Кроме того, полезно
иметь в виду, что если ДУ лежат параллельно поверхности образца с ориентацией
(111), то для того, чтобы увидеть хоть какой-то контраст, нужно наклонить образец,
иначе gR = 0 для любого g, лежащего в плоскости дефекта. На рис. 10.4 показаны две
типичные пары BF/DF одного и того же ДУ. В BF контраст внешних линий тот же
самый, либо белый, либо темный, а в DF контраст внешних линий – дополнителен
верхний темный, нижний белый или наоборот. Два закономерных вопроса возникают,
что определяет знак контраста и почему два изображения в режиме BF не являются
дополнительными?
Рис. 10.4. Темнопольное и светлопольное изображения дефекта упаковки.
Анализ показывает, что полярность контраста определяется фазовым членом в
(10.5), содержащим gR: в в изображении на экране, контур, соответствующий
поверхности будет светлым в BF, если gR > 0 и темным, если gR < 0. Расчет
интенсивности для дифрагированного пучка проведем в колонковом приближении.
Если дефект обрезает колонку на глубине t1, то используя ур-я (10.16, 10.17) имеем
φg = (iπ/ξg) {∫0t1 exp(-2πisz)dz + exp(-iα)∫t1t exp(-2πisz)dz}
(10.19)
что дает
φg = [iπ/(sξg)]exp(-2πist1){sin(πst1) + exp(-iα) sin[πs(t-t1)]}
(10.20)
Для интенсивности получаем
Ig = [1/(sξg)2][sin²(πst1+α/2)+sin²(α/2)
-sin(α/2)sin(πst+α/2)cos(2πst’)]
(10.21)
где t’ = t1-t/2, как на рис. 10.2. Так что контраст зависит как от толщины, так и от
глубины. Величина α для данного типа дефектов фиксирована и если t тоже можно
считать постоянной в исследуемой области локализации дефекта, тогда (10.21) дает
Ig ∝ (1/s²)[A – Bcos(2πst’)].
(10.22)
Т.о., так же как и для идеального кристалла, мы имеем осцилляции интенсивности по
глубине залегания дефекта с периодом 1/s, а сама интенсивность зависит от параметра
отклонения как s-2.
В случае накладывающихся ДУ, скажем 1-й дефект на глубине t1, а 2-й на
глубине t2, уравнение (10.19), соответственно усложняется:
6
φg = (iπ/ξg) {∫0t1 exp(-2πisz)dz + exp(-iα1)∫t1t1+t2 exp(-2πisz)dz
+ exp[-i(α1+α2)∫t1+t2t exp(-2πisz)dz }.
(10.19)
При этом контраст BF/DF не будет дополнительным.
В случае 3-х ДУ контраст исчезает
поскольку эффективное смещение R будет равно
нулю,
поскольку
3×(1/3)[11-1]
будет
восстанавливать идеальную решетку. Пример
такого исчезающего контраста показан на рис.10.5
[30].
Рис.10.5. Исчезающий контраст
при наложении 3-х ДУ в
нержавеющей стали.
Рис.10.6. Схема возникновения
трансляционного π-дефекта
Рис. 10.7. ДУ в шпинеле. а) –BF, б) –
схема образования ДУ/АФГ.
π- и δ- контуры
В изображениях упорядоченных интерметаллидов типа Ni3Al могут возникать т.н. πконтуры. Природа дефекта, вызывающего соответствующий контраст поясняется на
рис. 10.6. Интерметаллид имеет структуру типа L12, подобную гцк-решетку, в которой
атомы Al находятся в углах ячейки, образуя между собой простую кубическую
решетку. Дефект возникает за счет когерентной трансляции кристалла на R= ½ [110].
Изображение дефекта получается в DF с (100) рефлексом, который запрещен в
неупорядоченной решетке, а в упорядоченной является рефлексом сверхрешетки.
7
Трансляционные границы распространены в окислах. Как правило в них ячейка
большая, что повышает вероятность возникновения такого рода интерфейсов. На рис.
10.7 изображен дефект в шпинеле (MgAl2О4) [31,32]. Контраст изображения, как видно
из рис. 10.7а зависит от того какой рефлекс используется для DF. На рис. 10.7б
изображена схема образования дефекта. соответствующая трансляции на R=1/4[101].
Крупные кружки изображают анионы кислорода на различных уровнях (1,3), мелкие
кружки и треугольники – катионы на различных уровнях (1-4). Дефект имеет все
признаки ДУ в гцк материалах,
одновременно он относится и к АФГ,
поскольку трансляционный вектор
R=1/4[101]
–
идеальный
вектор
кислородной
подрешетки.
Если
Рис. 10.8.Контраст АФГ в TiO2.
использовать
рефлекс
220
для
изображения дефекта, то 2πgR = π (πдефект) и дефект хорошо виден, в то
время как для DF с 440 2πgR = 2π и
дефект виден лишь за счет остаточного
несоответствия, ввиду того что R не
точно равно 1/4[101].
Аналогичным образом, виден Рис. 10.9. АФГ (ИДГ) дефект в GaAs.
контраст на рис. 10.8, обусловленный
накладывающимися АФГ в TiO2[32]. Вектор трансляции R=1/2[01-1].
На рис. 10.9а приведено изображение АФГ в GaAs. Этот плоский дефект
известен еще под названием инверсионная доменная граница (ИДГ) (Inversion Domain
Boundary - IDB). Наблюдаемые контуры являются также трансляционными, но R не
соотносится простым способом к структуре решетки [33]. Из схемы на рис. 10.9б
видно, что трансляция обусловлена некоторой релаксацией связей Ga-Ga и As-As на
интерфейсе {110}. Значение R ≈0.019±0.003 нм. Ввиду малости R эти контуры
называют δ-контурами. Величину R определяют с использованием компьютерного
моделирования дефектов.
8
На практике встречаются
классифицированы в Табл.10.2.
Границы фаз
несколько видов
Табл. 10.2. Некоторые виды границ.
Граница
Пример
материала
Границы ферромагнитных доменов NiO
Границы
BaTiO3
ферроэлектрик/пьезоэлектрик
Композиционные границы раздела
GaAs/AlGaAs
Структурные границы раздела
α-SiC/β-SiC
гпу-Со/гцк-Со
Nb/Al2O3
Al/Cu
α-Fe/Fe3C
Композиционно-структурные
интерфейсы
фазовых
границ,
которые
Примечания
Небольшие
тетрагональные
искажения
ξg различно по обе
стороны от интерфейса
На рис. 10.10 изображен пример ФГ для NiO. Этот материал испытывает структурный
переход
из
кубической
в
ромбоэдрическую ферромагнитную фазу
в точке Кюри. Кубическую структуру
можно определить как частный случай
ромбоэдрической с углом α=60º в
ромбоэдре. Тогда ниже ТС этот угол
изменится только на 4.2' от α=60º. Т.о.,
большинство
g-векторов
лишь
незначительно повернутся и изменят
вектор отклонения s. Однако, как видно
из рис. 10.10, это незначительное
вращение уверенно детектируется по
Рис.10.10. ФГ в NiO вблизи точки Кюри.
измененному контрасту и слабым
контурам на границе фаз.
Поля упругих напряжений
В предыдущей лекции мы видели, что изгибы кристаллографических плоскостей
изменяют условия дифракции и создают контраст в изображении. Изгибы также
возникают вследствие упругих напряжений вблизи дефектов. Смещение атома в точке
r на расстояние R(r) есть следствие деформации ε, вызванной напряжением σ.
Иллюстрацией к возникновению контраста упругих напряжений является схема
на рис. 10.11. За счет изгибов плоскостей условии Брэгга могут выполняться даже в
случае, когда плоскость вдали от дислокации не дифрагирует, рис. 10.11а. Заметим, что
контуры контраста смещены относительно проекции дислокации, как схематично
показано на рис. 10.11б. Изгибы плоскостей вокруг винтовой дислокации показаны на
рис. 10.12.
9
Воспользуемся опять уравнением Хови-Уэлана для оценки контраста от
напряжений. Согласно (10.3) для дефектного кристалла мы имели
dφg/dz = (πi/ξ0)φg + (πi/ξg)φ0 exp[-2πi(sz+gR)]
(10.20а)
(10.20б)
dφ0/dz = (πi/ξ0)φ0 + (πi/ξg)φg exp[2πi(sz+gR)].
Рис.10.11. Схема формирования
контраста упругих напряжений
Однако на этот раз мы сделаем другую
подстановку, а именно:
φ0s = φ0exp(-πiz/ξ0)
(10.21а)
φgs = φgexp(2πisz -πiz/ξ0 + 2πi gR).
Рис. 10.12. Изгибы плоскостей
(10.21б)
вблизи винтовой дислокации.
Тогда ур-я Хови-Уэлана приобретают вид
(10.22а)
dφ0s/dz = (πi/ξg)φgs(z)
dφgs/dz = (πi/ξg)φ0(z) + [2πi(s + g·dR/dz)]φgs(z).
(10.22б)
Опуская подиндекс s, последнее уравнение можно переписать как
(10.23)
dφg/dz = (πi/ξg)φ0(z) + 2πi sRφg.
Это уравнение выглядит так же как и (7.13а) за исключением того, что вместо s в
уравнении стоит sR, определяемая соотношением
sR = s + g·dR/dz
(10.24)
Т.о., все основные результаты, полученные в предыдущей лекции, скажем зависимость
от толщины, сохраняют силу, если заменить s на sR. Важно то, что примененный метод
решения позволяет анализировать случаи непрерывно изменяющегося R. Т.е., контраст,
обусловленный g·R, используется для дефектов с постоянным R, а для непрерывно
меняющегося R используется sR, что определяется g·dR/dz.
Контраст от одиночной дислокации
Анализ делаем в колонковом приближении, рис. 10.13 [16]. Поле смещений вокруг
одиночной дислокации описывается выражением [34]:
R = (1/2π){bφ+(1/4)[1/(1-ν)]·[be+b×u(2(1-2ν)ln r + cos 2φ)]}
(10.25)
Для удобства, R дано здесь в полярных координатах (r и φ), как показано на рис. 10.13),
b – вектор Бюргерса, be – компонента вектора Бюргерса, ориентированная по краю
дислокации, u – единичный вектор вдоль дислокационной линии, ν – отношение
Пуассона.
10
Мы рассмотрим два случая: винтовой и краевой дислокаций. Для винтовой дислокации
be =0, b параллелен u, так что b×u = 0. В
этом случае (10.25) приобретает вид:
R = b φ/(2π) =
= b /(2π) arc tg [(z-zd)/x]
(10.26)
Здесь, z и zd поясняются на рис. 10.13 [16].
Из этого уравнения видно, что g·R
пропорционально g·b. Поэтому при анализе
изображений дислокаций говорят о g·bконтрасте.
Рис.10.13. Эффект удаленной
дислокации в колонковом
приближении
Для краевой дислокации be = b и
g·R содержит два члена g·b и g·b×u. Рис.10.14. Изгиб плоскостей скольжения.
Происхождение
последнего
члена
обусловлено
изгибом
плоскостей
скольжения [34], как изображено на рис. 10.14. Этот изгиб усложняет анализ для
некоторых случаев.
В зависимости от знака g·R или g·b изображение дислокации будет
располагаться либо по одну, либо по другую сторону от проекции дислокационного
кора. При g·b = 0 контраст отсутствует, поскольку в этом случае дифрагирующие
плоскости параллельны R. Контраст может присутствовать в этом случае только лишь
за счет члена g·b×u.
Практическим руководством по наблюдению дислокаций в ПЭМ может быть
справочник [35], где также приведена достаточно обширная коллекция иллюстраций
для характерных типов дислокаций и дефектов. Здесь мы ограничимся лишь
некоторыми характерными иллюстрациями. Изображение дислокаций иллюстрируется
на рис. 10.15 и 10.16 [2]. На рис. 10.15 а,б,в дано светлопольное изображение с сильным
возбуждением рефлексов {11-1}(а) и {220}(б,в). Дислокации располагаются близко к
(111) поверхности сплава на основе Cu, имеющего низкую энергию для ДУ. В этом
случае парциальные дислокации могут разделяться и образовывать лентообразные
дефекты. Одиночная линия под стрелкой на (в) – дислокация с вектором Бюргерса
параллельным g, так что g·b =2. Три параллельных контура на (в) – три парциальных
дислокаций Шокли, имеющих одинаковые b, и образованных диссоциацией вектора
Бюргерса ½ <112>. Они отсутствуют на (б), поскольку в этом случае g·b =0.
Изображение с {11-1}(а) образовано наклоном образца ~20º от полюса 111 к полюсу
112 и показывает контраст от ДУ. Они не дали бы контраста с рефлексом 111,
поскольку g·R в этом случае либо 0, либо целое.
11
Рис.10.15. а-в: BF с {11-1}(а) и {220}(б,в).
Дислокации располагаются близко к (111)
поверхности сплава на основе Cu, имеющего
низкую энергию для ДУ.
г,д: Дислокации в Ni3Al в фольге с (001)
ориентацией
с
двумя
ортогональными
рефлексами {220}.
Рис. 10.16. а: Сложная дислокация,
пересекающая границу доменов.
б,в: Дислокации на интерфейсе (001)
между двумя III-V компаундами с
небольшим несоответствием решеток.
Дислокационные петли и диполи
Вакансии и междоузельные атомы, образующиеся при облучении материалов, при
коалесценции образуют дислокационные петли (ДП). Существует несколько типов
дислокационных петель [34]. Если вектор Бюргерса лежит в плоскости петли, то ее
называют скользящей; если же он не лежит в ней (в частности, перпендикулярен), то
такую петлю именуют призматической. Формирование контраста обсуждается и
иллюстрируется в [35]. Представление о формировании контраста ДП дает схема на
рис. 10.17. Отметим следующие особенности.
-ДП имеют либо положительные, либо отрицательные b.
-Могут присутствовать также ДП, которые не дают g·b –контраста.
-ДП могут включать одиночные и кратные ДУ, и т.о. давать контраст как на рис.
10.18 [36].
-Особый случай – дислокационные диполи, демонстрирующие пример
взаимодействия дислокаций, рис. 10.19 [37]. ПЭМ – наилучший способ демонстрации
диполей, поскольку они не дают дальнодействующих напряжений и имеют
результирующий вектор Бюргерса, равный нулю.
12
Рис. 10.18. ДП в облученном
демонстрируют контраст ДУ.
Ni
Рис.
10.17.
Схема
формирования
контраста ДП. (а,б) междоузельные, (в,г)
вакансионные ДП. Внутренний контраст Рис. 10.19. Призматические ДП в Zn,
– вращение по часовой стрелке, внешний параллельные поверхности (0001).
контраст – вращение против часовой
стрелки.
Изображение в моде слабый-пучок темное-поле (WBDF)
Термин «микроскопия в слабых пучках» подразумевает формирование
изображения как в DF, так и в BF. Темнопольная микроскопия получила более широкое
распространение частично из-за того, что этот метод более понятен теоретически.
WBDF с успехом используется для изображения дислокаций в виде узких линий с
шириной ~ 1.5 нм. Позиция этих линий по отношению к дислокационному кору
достаточно хорошо определена. Она не очень чувствительна к толщине фольги и к
глубине расположения дислокации. В
частности, WBDF очень полезен при
исследовании диссоциированных дислокаций, где пары парциальных дислокаций могут
быть на расстоянии только ~4 нм и это разделение все же сильно влияет на свойства
материалов.
Метод состоит в выборе определенного g и перемещении его на оптическую ось,
Рис.10.20.
а) Сфера Эвальда пересекает ряд
регулярных рефлексов на расстоянии ng, где n не
обязательно целое. б) Схема положений Кикучилиний при возбуждении 4g.
как при формировании обычного CDF (Л9), рис. 10.20. Затем образец наклоняется и
13
устанавливается достаточно большое sg и наблюдают DF с использованием этого g.
Если дефект присутствует, то дифрагирующие плоскости могут изгибаться так, что
условие Брэгга по-прежнему выполняется и эти участки плоскостей будут давать
светлый контраст.
Проблема состоит в том, что по мере увеличения sg средняя интенсивность
падает как 1/s², пятно в ДК становится слабым. При этом, взаимодействие прямого и
дифрагированного пучков мало – выполняются условия, близкие к кинематическим.
На рис. 10.21 схематично поясняется метод возбуждения выбранного рефлекса.
Простое геометрическое рассмотрение приводит к соотношению
n = 2m –N,
(10.27)
где ng расстояние в обратном пространстве от начала координат до точки пересечения с
первой зоной Лауэ, mg – локализация Кикучи линии и N –ближайший рефлекс к
Кикучи-линии. Величина s может быть определена из соотношения
s = (1/2)(n-1)|g|²λ.
(10.28)
На рис. 10.21 и 10.22 приведены примеры использования WBDF [2].
Рис.10.21. WBDF контуры толщины в
отожженном
MgO
(А),
(В,С)
увеличенное
изображение
в
выделенных участках
Рис.10.22.
Сопоставление
дислокационных контуров в сплаве на
основе Cu. (А) – WBDF, (В) – сильный
пучок с sg>0.
Дифракция в кристаллах с дефектами двойникования
Двойникование может происходить, например, при пластической деформации,
рекристаллизации и фазовых превращениях. Двойники могут возникать в результате
деформации сдвига, при которой все атомные положения по одну сторону
границы(плоскости) двойникования связаны зеркальным отражением с атомными
положениями по ее другую сторону. Иначе говоря, двойникование можно описать как
поворот на 1800 вокруг оси двойникования. Плоскостями двойникования для гцк и оцк
кристаллов являются {111} и {112}, соответственно.
14