CОВРЕМЕННЫЕ ПРОЦЕССЫ ЭМУЛЬГИРОВАНИЯ И КОАЛЕСЦЕНЦИИ В ГИДРОМЕХАНИЧЕСКИХ ДИСПЕРГАТОРАХ. Булавин Д.О., Козлов В.В.
реклама

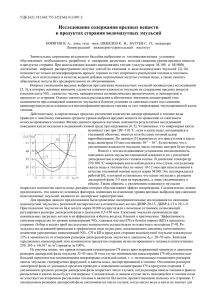
CОВРЕМЕННЫЕ ПРОЦЕССЫ ЭМУЛЬГИРОВАНИЯ И КОАЛЕСЦЕНЦИИ В ГИДРОМЕХАНИЧЕСКИХ ДИСПЕРГАТОРАХ. Булавин Д.О., Козлов В.В. Московский государственный университет технологий и управления им.К.Г.Разумовского Аннотация: Эмульгирование – процесс получения микрогетерогенных дисперсных систем, состоящих из трех жидких фаз: дисперсной фазы, образующей изолированные друг от друга капли диаметром (0,1 – 10) мкм; сплошной дисперсионной среды; межфазного поверхностного слоя, разделяющего капли дисперсной фазы инепрерывную дисперсионную среду, образующие в целом дисперсную систему. Ключевыеслова: эмульгирование, коалесценция, гидромеханические диспергаторы Abstract: Emulsification - the process of obtaining microheterogeneous disperse systems consisting of three liquid phases: a dispersed phase forming mutually isolated droplets of diameter (0.1 - 10) microns, a solid dispersion medium; interfacial layer separating the droplets of the dispersed phase and a continuous dispersion medium forming the disperse system as a whole. Keywords: emulsification,coalescence, hydraulic-mechanical dispersing medium Введение и постановка задачи Термодинамически эмульсии при поверхностных натяжениях на границе раздела жидких фаз больше 10-2 Н/м2являются неустойчивыми и их хранение сопровождается процессом коалесценции. При меньших поверхностных натяжениях осуществляется самопроизвольное эмульгирование под действием теплового движения молекул и капель (броуновское движение), приводящее к термодинамически устойчивых коллоидных систем. возникновению Для повышения стабильности эмульсий применяют эмульгаторы – дифильные поверхностно-активные вещества, снижающие межфазное поверхностное натяжение и образующие на границе раздела капли и дисперсионной сложной среды третью фазу – прочный стабилизирующий слой – так называемый структурно-механический барьер, препятствующий коалесценции [1, 2]. В образовании стабилизирующих слоев в эмульсии принимают участие частицы высокодисперсных суспензий, возникающих в результате химической и кавитационной эрозии и коррозии внутренних поверхностей пар трения гидравлического тракта, например, гидромеханизированных механических комплексов. Коалесценция – слияние капель или пузырей в эмульсиях, пенах и туманах. Она протекает самопроизвольно с уменьшением свободной поверхностной энергии вследствие уменьшения общей поверхности коалисцирующих капель или пузырей. Коалесценция – характерная для легкоподвижных поверхностей раздела жидкость-газ (пена) или жидкость 1 (дисперсионная среда) – жидкость 2 (дисперсная фаза) и межфазный поверхностный слой. Наиболее глубокая стадия коагуляции капель – полное расслоение и разрушение эмульсии на две жидкости. Для общности иногда процесс эмульгирования называют диспергированием, в частности, измельчение одной жидкости на капли распределенные в другой непрерывной дисперсионной среде, образуя жидкую дисперсную систему. Капли эмульсии можно характеризовать удельной поверхностной энергией на единицу массы капли: Eп = ∙ = где Eп – поверхностная энергия капли, , (1) m– масса капли, d–диаметр капли, F– площадь поверхности капли, – плотность жидкости капли, σ = σ −σ (2) - абсолютное значение коэффициента межфазного поверхностного натяжения на границе раздела дисперсной фазы и дисперсионной среды, - поверхностное натяжение дисперсионной среды относительно воздуха атмосферы, - поверхностное натяжение дисперсной фазы относительно того же газа. Из (1) следует, что cуменьшением капли эмульсии ее удельная поверхностная энергия возрастает обратно пропорционально диаметру капли. Вычислим удельную поверхностную энергию эмульсии равную удельной поверхности всех капель, которые находятся в единице объема эмульсии: Eуд.э = σΝ, (3) где Ν – концентрация капель эмульсии. Из условия постоянства объемной концентрацииСэ эмульсии в процессе эмульгированияследует, что: Сэ = d Ν, (4) , (5) и следует, что: Ν= Сэ где d, Ν – характерный диаметр капель и их концентрация в любой момент времени процесса диспергирования. Отношение (3) с учетом (5) примет вид: Eуд.э = Сэ σD, (6) Удельная поверхностная энергия капли (1) и эмульсии прямо пропорциональна дисперсности эмульсии D = d . Для последующего нам понадобится соотношение, которое вытекает из баланса объема дисперсной фазы: Сэ = d Ν= d Ν , (7) или: d Ν = d Ν , где d , Ν (8) – характерный диаметр капель в эмульсии и их концентрация в начальный момент времени процесса эмульгирования. Из вышеизложенного следует, что с увеличением дисперсности эмульсии удельная поверхностная энергия капли (1) и эмульсии (6) возрастает. Влияние диаметра капли на ее распад Роль энергии увеличивается, с межфазного увеличением поверхностного дисперсности натяжения эмульсии, т.е. с уменьшением диаметра капли для ее разрушения необходимо затратить больше удельной энергии (на единицу массы или объема). Исходя из этого факта, рассмотрим вероятность распада капли, с учетом того, что она зависит от ее диаметра. Предполагая, что в процессе эмульгирования вероятность дробления капли равна λ, то за время dtвозникнетdΝновых капель, причем: dΝ = λΝdt. (9) Примем, что в аппаратах-эмульгаторах с основным фактором воздействия – тангенциальных напряжений F [3]: λ =λ где = (10) – частота вращения капли в неоднородном поле тангенциальных напряжений с линейным ускорениемa на ее экваторе, λ - характерный параметр аппарата-эмульгатора и режима его работы. С учетом одновременного процесса коалесценции капель эмульсии [4]: dΝ = − где √ΝΝ dt, (11) –коэффициент коалесценции, зависящий от аппарата-эмульгатора, физико-химических свойств компонентов эмульсии. В частности, при → 0dΝ → ∞, то есть коалесценция не наблюдается, так как наблюдается самопроизвольное эмульгирование. Физическая модель и экспериментальное исследование Объединяя выражения (9) - (11), получим физическую модель в виде дифференциального уравнения, которое описывает совмещенные процессы эмульгирования и коалесценции в аппарате эмульгаторе с тангенциальными напряжениями: / / σ= dt, (12) которое имеет решение в виде конечного ряда суммы [4]. Постоянная интегрирования определяется из начального условия: t = 0, Ν = Ν (13) Экспериментальное исследование процесса эмульгирования в роторных аппаратах типа ГМД показало, что λ - характерная постоянная аппарата-эмульгатора зависит от режима работы аппарата [5] (рис.1), где изображена зависимость эффективности аппарата- эмульгатора типа ГМД (λ (dD/dt)|t = 0) от градиента скорости в зазоре между ротором и статором.Заметим, что на рис. tga = (dD/dt)|t = 0.Из рис.1 следует, что при каких-то градиентах скоростиωR/δ = 1,2∙ tga ∙10 105C -3 резко возрастает от 103 (м ∙ с2)-1 20 до 2,4∙104 (м∙с2)-1, 16 т.е. примерно в 12 24 раза. 8 4 0 Рис.1. 4 12 Зависимость 28 36ωR/δ∙10-4, c-1 20 эффективности роторного аппарата-эмульгатора от градиента скорости в зазоре между ротором и статором [5]. Выводы Резкое увеличение характерного параметрааппарата–эмульгатора, вероятно, связано с переходом от докавитационного режима работы аппарата к кавитационному режиму работы. При этом вероятность распада капель эмульсии увеличивается также на три порядка. Отсюда видно, что кавитация в ГМД является мощным интенсифицирующим фактором воздействия на совмещенный процесс эмульгирования при наличии процесса коалесценции. С целью оптимизации процесса эмульгирования необходимо рассчитывать аппараты-эмульгаторы на максимальное возбуждение импульсной кавитации, когда вероятность распада капель будет максимальной. Литература 1. Гопал Е.С.Р. Принципы получения эмульсий. В кн. Эмульсии. Пер. с англ. Под ред. Докт. Техн. Наук А.А.Абрамзона. Издательство «Химия», л.: 1972. С. 9 – 74. 2. Воюцкий С.С. Курс коллоидной химии. М.: 1964. С. 395 – 410. 3. Юдаев В.Ф., Колач С.Т., Алексеев В.А. Кинетика эмульгирования жидкости в аппаратах-эмульгаторах со сдвиговыми потоками. Строительные материалы, оборудование, технологии XXI века. N1. 2010. С. 32 – 33. 4. Колач С.Т. Эмульгирование с учетом коагуляции в аппаратах с тангенциальными напряжениями. Автореф. дис. … канд. техн. наук. М.: 2011. 5. Колач С.Т. Эмульгирование с учетом коагуляции в аппаратах с тангенциальными напряжениями. Дис. … канд. техн. наук. М.: 2011.