Определение плотности твердых тел правильной формы

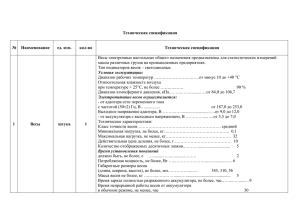
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Уральский государственный технический университет – УПИ»
Нижнетагильский технологический институт (филиал) УГТУ–УПИ
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДЫХ ТЕЛ
ПРАВИЛЬНОЙ ФОРМЫ
Методические указания к лабораторной работе
Нижний Тагил
2008
УДК 531.754(076)
Составитель: А. А. Ходырев
Научный редактор: Т.М. Гаврилова
Утверждено на заседании кафедры общей физики НТИ (ф) УГТУ – УПИ
(протокол № 4 от 15.05.2007 г.)
Определение плотности твердых тел правильной формы [Электронный
ресурс] : метод. указания к лаб. работе № 1 для студентов всех специальностей
НТИ (ф) УГТУ – УПИ / сост. А. А. Ходырев. – Нижний Тагил : НТИ (ф) УГТУ –
УПИ, 2008. – 19 с.
В работе описан метод определения плотности твердых тел правильной
формы путем определения линейных размеров тела и взвешивания. Описан порядок выполнения работы и оформления отчета.
Библиогр.: 8 назв. Рис. 6. Прил. 1.
Подготовлено кафедрой «Общая физика»
2
ВВЕДЕНИЕ
В данной работе определяется плотность твердых тел. Плотностью однородного тела называется физическая величина, численно равная массе единицы
его объема:
m
ρ=
(1)
V
где m - масса тела,
V - объем тела.
Как видно из формулы (1), для нахождения плотности тела необходимо
знать его массу и объем. Масса определяется взвешиванием на весах. Так как тела,
исследуемые в работе, имеют правильную геометрическую форму, то для определения объема достаточно измерить их линейные размеры и произвести соответствующие вычисления.
ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ РАЗМЕРОВ
Для определения линейных размеров существуют различные приборы. Ниже
рассмотрено устройство используемых в лабораторной работе приборов: штангенциркуля и микрометра - и порядок выполнения ими измерений.
Масштабная линейка и нониус
При измерении длины масштабной линейкой можно вполне точно определить содержащееся в измеряемой длине целое число миллиметров, но доли миллиметра точно определить нельзя.
Для отсчета десятых и сотых долей миллиметров масштабную линейку
снабжают дополнительным устройством, называемым нониусом. Применение нониуса основано на способности человеческого глаза точнее оценивать совпадение
штрихов, нежели расстояние между несовпадающими штрихами. Нониус представляет собой маленькую линейку, свободно передвигающуюся вдоль масштабной линейки.
Нониус разделен на некоторое число делений n с таким расчетом, чтобы его
длине на масштабной линейке соответствовало число делений линейки либо на
единицу меньше (n-1) для одного типа (рис. 1,a), либо на 9 единиц больше (2n-1)
для другого типа нониусов (рис. 1,б).
3
Рис.1. Схема устройства нониусов двух типов:
1-масштабная линейка, 2- нониус
Таким образом, линейный размер одного деления нониуса оказывается несколько меньше одного (см. рис.1,а), либо двух (см. рис.1,б) делений масштабной
линейки.
Разность между линейным размером одного (рис.1,а) или двух (рис.1,б) делений масштабной линейки линейным размером одного деления нониуса называется точностью нониуса или его постоянной.
Если а - линейный размер одного наименьшего деления масштабной линейки, b - линейный размер одного деления нониуса и n - число делений нониуса, то
для нониуса первого типа (см. рис.1,а) имеем nb=(n-1)a, откуда его точность
a
(2)
a −b =
n
для нониуса второго типа (см. рис.1,б) nb=(2n-1)a, откуда точность нониуса
a
(3)
( 2a − b) =
n
Следовательно, точность нониуса численно равна отношению величины
наименьшего деления масштабной линейки к числу делений нониуса.
На рис. 1,а и 1,б изображены нониусы, точность которых равна 1/10 деления
масштаба. Бывают нониусы с точностью 1/5, 1/25, 1/50 и1/100 деления масштаба.
Измерение длины какого-либо тела (образца) масштабной линейкой с нониусом производится следующим образом. Масштаб прикладывается своим нулевым делением к одному краю образца (рис. 2.), а к другому подводится нулевое
деление нониуса. Отсчитывают целое число делений масштабной линейки, находящееся слева от нуля нониуса (на рис. 2 – три деления). Затем смотрят, какое деление нониуса сливается в одну линию с делением масштабной линейки. Номер
совпавшего деления нониуса (на рис.2 – 6-е деление) умножают на точность нониуса (1/10) и получают дробную часть длины образца (6/10). Окончательный ре4
зультат измерения равен сумме найденных величин 3,6 деления. Таким образом,
прежде чем пользоваться нониусом, нужно знать его точность.
Рис.2. Измерение длины образца масштабной линейкой с нониусом:
1-образец, 2- масштабная линейка, 3- нониус.
Штангенциркуль
Для измерения линейных размеров тел чаще пользуются не простой масштабной линейкой, а особым прибором - штангенциркулем. Штангенциркуль
(рис.3) представляет собой масштабную линейку (с делениями через 1 или 0,5 мм),
на конце которой имеется клювовидный выступ A.
На линейку надета скользящая обойма с прорезью, снабженная выступом В.
На скосе прорези обоймы нанесены деления нониуса. Когда выступы масштабной
линейки и обоймы сдвинуты вплотную друг к другу, нулевые деления масштаба и
нониуса совпадают. Кроме того, штангенциркуль обычно снабжен дополнительными выступами A' и B', позволяющими определять внутренние размеры предмета
(например, внутренний диаметр трубок). У некоторых штангенциркулей на масштабную линейку надет еще хомутик с микровинтом 6 и винтом 3. Для измерения
размеров предмета его помещают между выступами A и B, закрепляют хомутик
винтом 3 и с помощью микровинта 6 зажимают предмет (без больших усилий) так,
чтобы он не выпадал из выступов. Затем винтом 2 зажимают обойму и отсчитывают длину по масштабной линейке и нониусу, как указано выше (см. рис.2). Предел основной погрешности штангенциркулей равен точности их нониусов (ГОСТ
166-73). Так, если точность нониуса равна 0,1 мм, то погрешность измерения равна ±0,1 мм.
5
Рис.3. Общий вид штангенциркуля:
1-обойма, 2 и 3- винты обоймы и хомутика, 4-масштабная линейка, 5-хомутик, 6микровинт, 7-нониус.
Микрометр
Для измерения малых наружных размеров с точностью до 0,01 мм применяется микрометр. Основной частью его является микрометрический винт (рис.4),
который применяется также в целом ряде приборов: сферометрах, компараторах,
инструментальных микроскопах и др.
Микрометрический винт состоит из винтовой пары (гайка-болт) с малым
шагом винта.
Рис.4. Принципиальная схема измерения малых линейных размеров (а) и примеры
отсчета с помощью микрометрического инструмента (б и в):
(L1 = (5,00 + 0,27) мм = 5,27 мм; L2 = (5,50 + 0,25) мм = 5,75 мм)
6
Устройство микрометрического винта основано на том, что линейное перемещение винта прямо пропорционально величине шага и углу поворота:
l=h
ϕ
2π
(4)
где l - линейное перемещение винта,
ϕ - угол поворота винта в радианах,
h - шаг винта - смещение барабана вдоль линейной шкалы за один оборот.
Из рисунка 4,а видно, что при движении точки A по винтовой линии с небольшим углом подъема α ее малые линейные перемещения l в осевом направлении значительно легче и точнее измерять, отсчитывая их угловое перемещение. С
этой целью на окружности отсчетного барабана нанесено деление (рис.4,б), позволяющие отсчитывать малые линейные перемещения винта. Для измерения числа
целых оборотов служит линейная шкала.
Пусть h - шаг винта, n - число делений, на которое разделен барабан. Тогда
цена деления микрометрического инструмента, соответствующая его повороту на
одно деление барабана, равная отношению шага винта к числу делений круговой
шкалы, называется точностью:
h
(5)
l=
n
Например, если шаг винта h=0,5 мм, а число делений на барабане n = 50, то
точность круговой шкалы
l=
0,5
= 0,01 мм/дел.
50
Размер L предмета, измеряемый микрометрическим инструментом, определяется расстоянием от края скоса барабана до нулевого деления линейной шкалы
инструмента. Следовательно, длина предмета с точностью до 0,5 деления отсчитывается по линейной шкале, а десятые и сотые доли миллиметра - по круговой
шкале барабана. Примеры отсчета указаны на рис.4,б и в.
Микрометр состоит (рис.5) из скобы 1, на которой крепятся основные детали, неподвижной пятки 2, вращающегося шпинделя 3 с микровинтом, стопорного
винта 4 для закрепления шпинделя, гильзы 5 с линейкой (основной) шкалой 6, барабана 8 с круговой шкалой 7, колпачка 9 для крепления барабана на шпинделе и
трещотки 10, служащей для равномерного нажатия шпинделя на измеряемый образец.
Линейная шкала 6 на гильзе 5, деления которой нанесены через 1 мм, представляет из себя две шкалы, сдвинутые относительно друг друга на 0,5 мм и разделенные прямой линией. В результате этого нижняя шкала делится верхней пополам. Скошенный край барабана 8 разделен на 50 делений и при вращении дви-
7
жется поступательно вдоль линейной шкалы микрометра, смещаясь при этом на
0,5 мм за 1 оборот.
Рис.5. Общий вид микрометра:
1-скобка, 2-пятка, 3-шпиндель, 4-стопорный винт, 5-гильза, 6-линейная
шкала, 7-шкала барабана, 8-барабан, 9-колпачок, 10-трещотка.
Перед работой с микрометром необходимо проверить правильность установки нуля. Для этого необходимо, вращая барабан при помощи трещотки, привести в соприкосновение шпиндель с пяткой. При правильной установке нуля,
скошенный край барабана должен проходить через нуль линейной шкалы, а нуль
круговой шкалы барабана - совпадать с горизонтальной линией основной шкалы.
(Установка нуля производится дежурным лаборантом).
Измерения с помощью микрометра производятся в следующем порядке.
Предмет помещают между пяткой 2 и шпинделем 3 и, вращая барабан при помощи трещотки 10, доводят шпиндель до упора о поверхность предмета, сигналом
чего служат щелчки трещотки. По линейной шкале против скошенного края барабана отсчитывают целое число делений с точностью до 0,5 мм. Десятые и сотые
доли миллиметра отсчитывают по делению круговой шкалы, оказавшемуся против
горизонтальной линии основной шкалы, как это было указано выше (см. рис 4, б и
в).
Так как с помощью микрометра можно измерить с точностью до 0,01 мм, то
в качестве систематической погрешности при однократном измерении (а также
при многократных измерениях, дающих одно и то же значение) принимают половину этой величины, т. е. ±0,005 мм (ГОСТ 6507-60).
8
ВЗВЕШИВАНИЕ ТЕЛА
Масса тела в данной работе определяется взвешиванием на технических весах.
Рис.6. Технические весы:
1-основание, 2- колонка, 3- коромысло,
4,6-призмы, 5-стальная подушка, 7сережки, 8-чашки, 9-стрелка,10шкала, 11-арретир
Технические весы
состоят из пластмассового
основания
1
(рис.6), на котором крепится колонка весов 2.
Сверху на колонке располагается
основная
часть весов - равноплечее
коромысло
3,
имеющее в середине
призму 4, опирающуюся на стальную подушку 5.
На концах коромысла на одинаковых расстояниях от середины призмы 4 находятся еще две призмы 6, на которых с помощью сережек 7 подвешены две чашки 8.
К центру коромысел прикреплена длинная стрелка 9, фиксирующая отклонение коромысла от положения равновесия по шкале 10.
Для освобождения движущихся частей весов существует арретир, рукоятка
которого 11 расположена в нижней части основания весов.
При работе с весами необходимо соблюдать следующие правила:
1. Взвешивать на весах только такие тела, вес которых не превышает предельную
нагрузку весов (указывается на коромысле весов).
2. Класть на чашки весов или снимать с них взвешиваемые тела и разновески
можно только тогда, когда весы арретированы.
3. Взвешиваемый груз следует класть на левую чашку весов, а разновески на правую, при этом центр тяжести грузов и разновесок должен находиться посередине чашек.
4. Разновески следует брать только пинцетом. Разновески могут занимать только
два положения: в футляре и на правой чашке весов.
9
5. Освобождать и арретировать весы следует плавно и без толчков.
6. Не следует освобождать коромысло весов сразу полностью, пока весы еще не
вполне уравновешены; его следует освобождать лишь настолько, чтобы можно
было определить, какая из чашек легче. После каждой «пробы» весы снова арретируют и добавляют или снимают разновески.
7. При полностью освобожденном коромысле амплитуда колебаний стрелки
должна быть не менее 3-4 делений.
8. После взвешивания весы сразу арретируются, а груз и разновески снимаются с
чашек.
Существуют различные методы взвешивания. В данной работе применяется
метод простого взвешивания - на одной чашке. Рекомендуется следующая последовательность операций.
Определение нулевой точки ненагруженных весов. Нулевая точка (нуль,
точка равновесия) весов - это отделение шкалы, против которого останавливается
стрелка весов после прекращения колебаний.
Вследствие затухания колебаний последовательные отклонения стрелки от
нулевой точки уменьшаются. Поэтому взяв полусумму делений n1 и n2, против которых стрелка останавливается в двух последовательных крайних положениях, мы
не получим истинного положения нулевой точки. Необходимо взять нечетное
число максимальных отклонений стрелки. В нашей работе рекомендуется взять
два отклонения (n1 и n3) влево и одно отклонение (n2) - вправо.
Если нулевое деление шкалы находится посередине шкалы, то отклонение
стрелки влево считается отрицательными, а вправо - положительными. Тогда нулевая точка весов:
n1 + n3
+ n2
n0 = 2
2
Пример 1. Пусть n1= -5 дел., n2=2 дел., n3= - 4,5 дел. Тогда
− 5 − 4,5
+2
2
n0 =
= −1,375 = −1 (дел.)
2
т. е. нулевая точка весов находится слева от нуля шкалы. Здесь учитывается,
что ошибка при взвешивании принимается равной цене деления весов. Поэтому
результат округляется до целого значения.
Пример 2. Пусть n1= -3 дел., n2= 5 дел., n3= -2,5 дел.
Тогда
10
− 3 − 2,5
+5
2
no =
= 1,125 = 1 (дел.)
2
т. е. нулевая точка весов находится справа от нуля шкалы.
Определение нулевой точки нагруженных весов. Взвешиваемое тело положить на левую чашку весов, уравновесить его разновесками и способом, описанным выше, определить нулевую точку n0’ нагруженных весов. Записать массу
разновесок, лежащих на чашке весов.
Определение цены деления нагруженных весов. Цена деления весов - это
нагрузка, вызывающая отклонение стрелки на одно деление шкалы. Эта величина
зависит от нагрузки, поэтому ее определяют при нагруженных весах. К разновескам, уравновешивающим взвешиваемое тело, добавить перегрузок в m0 = 20÷50 мг
и вновь по качаниям стрелки определить нулевую точку n0".
Величина |n0"-n0'| дает число делений, на которое стрелка отклоняется от
первоначального положения равновесия n0' под действием дополнительной нагрузки m0. Разделив эту нагрузку m0 на |n0"- n0'|, получим цену деления a.
Определение массы взвешиваемого тела. Умножив цену деления на разность n0'-n0, где n0'-нулевая точка нагруженных весов (без перегрузки), n0 - нулевая
точка ненагруженных весов, получим добавку, которую, в зависимости от знака
n0'-n0 нужно прибавить (n0'-n0>0) или отнять (n0'-n0<0) от массы разновесок, лежащих на чашке весов, чтобы получить истинное значение массы взвешиваемого тела.
Пример 1. Пусть n0 =1 дел., n0' =5 дел., a = 4 мг/дел.
a (n0'-n0) = 4 (5-1) = 16 (мг).
Чтобы найти массу тела, к массе разновесок, лежащих на чашке весов, нужно прибавить 16 мг.
Пример 2. Пусть n0=1 дел., n0'=-6 дел., a=4 мг/дел.
a (n0'-n0)=4(-6-1)= -28 (мг).
Чтобы найти массу тела, от массы разновесок на чашке весов нужно отнять
28 мг.
Погрешность отсчитывания при взвешивании принимается равной цене деления весов.
11
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
В нашей работе объектами измерения служат цилиндрические тела, изготовленные из различных материалов. Если объем цилиндра
πd 2 h
(6)
V=
4
то формула (1) примет вид
4m
(7)
πd 2 h
где m - масса цилиндра,
d - диаметр образца,
h - высота образца.
Из формулы (7) видно, что для определения плотности цилиндра необходимо знать его высоту, диаметр и массу. Высоту измеряют штангенциркулем, а диаметр - микрометром. Так как высота и диаметр могут в разных местах оказаться
неодинаковыми, то их измерения следует производить не менее пяти раз каждое.
Для этого нужно при измерении высоты цилиндр поворачивать вокруг оси, а диаметр измерять в разных местах по высоте цилиндра. Результаты измерений записывают в таблицы отчета (см. Приложение). Среднее из полученных значений высоты и диаметра принимают за величину, наиболее близкую к истинной.
Наконец, взвешиванием на технических весах определяют массу цилиндра и
цену деления шкалы весов.
При проведении расчетов помните, что погрешность ∆ρ окончательного результата записывается с точностью до одной значащей цифры, а промежуточные
погрешности S, θ, ε, γ – с точностью до двух значащих цифр (значащие цифры
приближенного числа – все его цифры, кроме нулей, стоящих в начале числа).
Подробнее об обработке результатов измерений см. [3].
ρ=
12
Контрольные вопросы
1. Сформулируйте цель работы.
2. Перечислите основные измерительные операции и их последовательность.
3. Выведите формулу плотности для образца, имеющего цилиндрическую форму.
4. Что такое нониус? Как он устроен?
5. Что называется постоянной нониуса и как ее определить? Какова единица ее
измерения?
6. Как определить цену деления на барабане микрометра?
7. Как проверить правильность установки нуля микрометра?
8. Какова последовательность операций по определению длины, диаметра и массы
образца?
9. Что называют нулевой точкой весов и как ее определяют?
10. Какова последовательность операций при взвешивании тела на технических
весах?
11. Как находят абсолютную ошибку при взвешивании на технических весах?
13
Приложение
ФОРМА ОТЧЕТА
Т и т у л ь н ы й л и с т:
Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет – УПИ»
Нижнетагильский технологический институт (филиал) УГТУ-УПИ
Кафедра общей физики
ОТЧЕТ
по лабораторной работе № 1
«Определение плотности твердых тел правильной формы»
Студент(ка)_____________
Группа_________________
Дата___________________
Проверил_______________
На внутренних страницах:
1. Расчетная формула
4m
,
πd 2 h
где ρ - плотность материала;
m – масса цилиндра;
d – диаметр цилиндра;
h – высота цилиндра.
2. Средства измерений и их характеристики
ρ=
14
Предел изНаименование средмерений или
ства измерений и его
номинальное
номер
значение
Весы технические №
Штангенциркуль №
Микрометр №
Цена деления шкалы
Класс
точности
Предел основной погрешности θосн
3. Результаты измерений.
3.1. Измерение массы образца
m = ……….г;
Перегрузка: m0 = ……….мг;
Отклонение стрелки от положения равновесия при перегрузке на |n0"-n0'| =
……..делений;
Цена деления весов: a =
m0
n − n0'
''
o
= ……….мг
Основная погрешность в определении массы:
θосн = a (n0'-n0) = ……… мг
Абсолютная погрешность в определении массы:
∆m = θm = θОТСЧ 2 + θОСН 2 = ……….г,
где θотсч – погрешность отсчитывания, равная половине цены деления
весов.
3.2. Измерение диаметра образца
(di- ⟨d ⟩ ), мм
(di- ⟨d ⟩ )2, мм2
di, мм
n
(d i − ⟨d ⟩ )
∑
i =1
⟨d ⟩ = …..мм
Среднее квадратичное отклонение:
n
(d i − ⟨ d ⟩ ) 2
∑
i =1
= ……..мм.
n(n −1)
Граница случайной погрешности:
ε d = t ( P, n) S ⟨ d ⟩ = ………..мм,
где t(P,n) – коэффициент Стьюдента.
Граница неисключенной систематической погрешности:
S ⟨d ⟩ =
15
2
= ..... мм 2
θd = θосн = ……..мм.
Граница полной погрешности результата измерения диаметра:
2
∆d = ε d2 + θОСН
= …….мм.
Результат измерения диаметра:
⟨d ⟩ = ………..мм,
∆d = …………мм,
P = 0,95
3.3. Измерение высоты образца
(hi - ⟨h⟩ )2, мм2
(hi - ⟨h⟩ ), мм
hi, мм
n
(hi − ⟨ h⟩ ) 2 =….мм
∑
i =1
⟨h⟩ = ……..мм
2
Среднее квадратичное отклонение:
n
(hi − ⟨ h⟩ ) 2
∑
i =1
= ……….мм.
n(n −1)
Граница случайной погрешности:
ε h = t ( P, n)S⟨ h⟩ = …………мм.
Граница неисключенной систематической погрешности:
θh = θосн = ……..мм.
Граница полной погрешности результата измерения высоты:
2
= …….мм.
∆h = ε 2h + θОСН
Результат измерения высоты:
⟨h⟩ = ………..мм,
∆h = …………мм,
P = 0,95
4. Расчет искомой величины в СИ:
4m
ρ = 2 =………..кг/м3.
πd h
5. Оценка границы относительной погрешности результата измерения плотности:
S ⟨ h⟩ =
2
γ=
2
2
∆ρ
 ∆ m   ∆π   ∆ d   ∆ h 
= 
 + 
 +
 + 2
⟨ρ⟩
 m   π   d   h 
2
6. Оценка границы абсолютной погрешности результата измерения плотности:
3
∆ρ = γ ⟨ρ⟩ = ………..кг/м ,
P = 0,95.
7. Окончательный результат:
16
3
3
ρ = ⟨ρ⟩ ± ∆ρ = (……. ± ……)·10 кг/м ,
8. Выводы:
17
P = 0,95.
БИБЛИОГАФИЧЕСКИЙ СПИСОК
1. Алешкевич, В.А. Механика [Текст]: учеб. Для студ. Вузов / В.А. Алешкевич,
Л.Г. Деденко, В.А. Караваев; Под ред. В.А. Алешкевича. – М.: Издательский
центр «Академия», 2004. – 480 с.
2. Матвеев, А.Н. Механика и теория относительности [Текст] : учебн. Для студентов вузов / А.Н. Матвеев. – М. : ООО «Издательский дом «ОНИКС 21 век»:
ООО «Издательство «Мир и образование», 2003. – 432 с.
3. Савельев, И. В. Курс общей физики [Текст] : учеб. пособие для втузов : в 5 кн.
/ И. В. Савельев. – М. : Наука. Физматлит, 1998. – Кн. 2. Механика. – 336 с.
4. Сивухин, Д. В. Общий курс физики [Текст] : в 5 т. / Д. В. Сивухин. – М. : Наука. Физматлит, 2002. – Т. 1. Механика. – 560 с.
5. Кортнев, А. В. Практикум по физике [Текст] : / А. В. Кортнев, Ю. В. Рублев,
А. Н. Куценко. – М. : Высшая школа, 1965. – 568 с.
6. Руководство к лабораторным занятиям по физике [Текст] : / под ред.
Л. Л. Гольдина. – М. : Наука, 1983. – 704 с.
7. Евграфова, Н. Н. Руководство к лабораторным работам по физике [Текст] :
Учебное пособие для радиотехнических и электроприборостроительных специальностей вузов / Н. Н. Евграфова, В. Л. Каган. – М. : «Высшая школа», 1970. –
384 с.
8. Сидоров, А. А. Вычисление погрешностей в физическом лабораторном практикуме [Текст] : / А. А. Сидоров. – Екатеринбург : УГТУ – УПИ, 1993. – 15 с.
18