II. Экспериментальные исследования

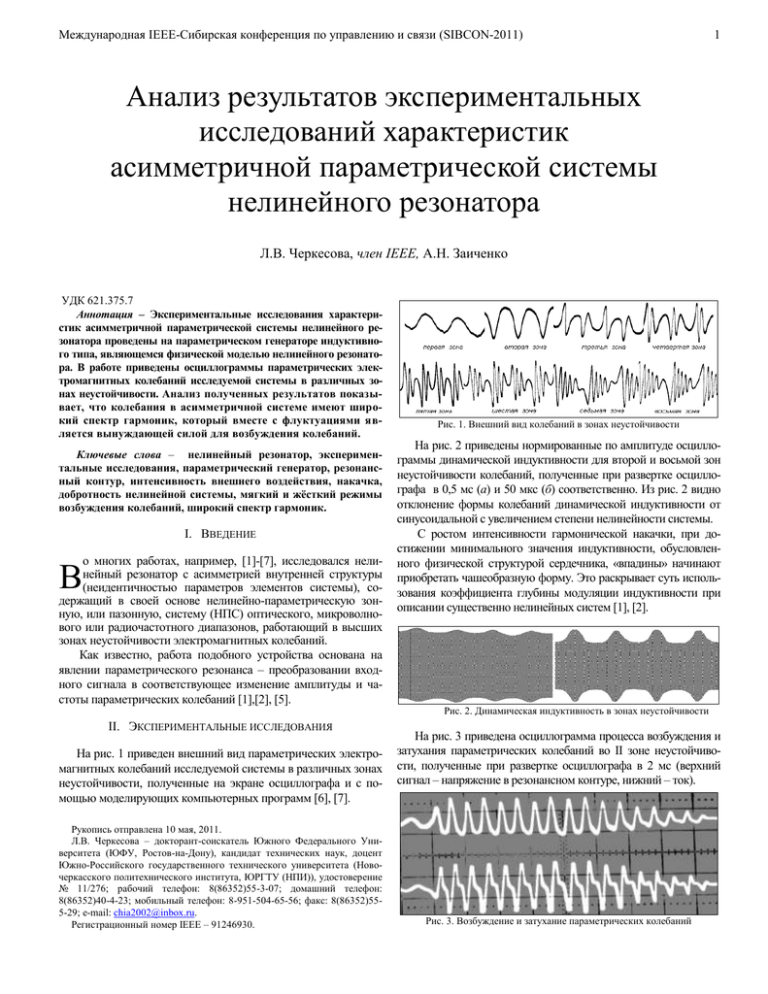
Международная IEEE-Сибирская конференция по управлению и связи (SIBCON-2011)
1
Анализ результатов экспериментальных
исследований характеристик
асимметричной параметрической системы
нелинейного резонатора
Л.В. Черкесова, член IEEE, А.Н. Заиченко
УДК 621.375.7
Аннотация – Экспериментальные исследования характеристик асимметричной параметрической системы нелинейного резонатора проведены на параметрическом генераторе индуктивного типа, являющемся физической моделью нелинейного резонатора. В работе приведены осциллограммы параметрических электромагнитных колебаний исследуемой системы в различных зонах неустойчивости. Анализ полученных результатов показывает, что колебания в асимметричной системе имеют широкий спектр гармоник, который вместе с флуктуациями является вынуждающей силой для возбуждения колебаний.
Ключевые слова – нелинейный резонатор, экспериментальные исследования, параметрический генератор, резонансный контур, интенсивность внешнего воздействия, накачка,
добротность нелинейной системы, мягкий и жёсткий режимы
возбуждения колебаний, широкий спектр гармоник.
I. ВВЕДЕНИЕ
о многих работах, например, [1]-[7], исследовался нелинейный резонатор с асимметрией внутренней структуры
(неидентичностью параметров элементов системы), содержащий в своей основе нелинейно-параметрическую зонную, или пазонную, систему (НПС) оптического, микроволнового или радиочастотного диапазонов, работающий в высших
зонах неустойчивости электромагнитных колебаний.
Как известно, работа подобного устройства основана на
явлении параметрического резонанса – преобразовании входного сигнала в соответствующее изменение амплитуды и частоты параметрических колебаний [1],[2], [5].
В
II. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
На рис. 1 приведен внешний вид параметрических электромагнитных колебаний исследуемой системы в различных зонах
неустойчивости, полученные на экране осциллографа и с помощью моделирующих компьютерных программ [6], [7].
Рукопись отправлена 10 мая, 2011.
Л.В. Черкесова – докторант-соискатель Южного Федерального Университета (ЮФУ, Ростов-на-Дону), кандидат технических наук, доцент
Южно-Российского государственного технического университета (Новочеркасского политехнического института, ЮРГТУ (НПИ)), удостоверение
№ 11/276; рабочий телефон: 8(86352)55-3-07; домашний телефон:
8(86352)40-4-23; мобильный телефон: 8-951-504-65-56; факс: 8(86352)555-29; e-mail: [email protected].
Регистрационный номер IEEE – 91246930.
Рис. 1. Внешний вид колебаний в зонах неустойчивости
На рис. 2 приведены нормированные по амплитуде осциллограммы динамической индуктивности для второй и восьмой зон
неустойчивости колебаний, полученные при развертке осциллографа в 0,5 мс (а) и 50 мкс (б) соответственно. Из рис. 2 видно
отклонение формы колебаний динамической индуктивности от
синусоидальной с увеличением степени нелинейности системы.
С ростом интенсивности гармонической накачки, при достижении минимального значения индуктивности, обусловленного физической структурой сердечника, «впадины» начинают
приобретать чашеобразную форму. Это раскрывает суть использования коэффициента глубины модуляции индуктивности при
описании существенно нелинейных систем [1], [2].
Рис. 2. Динамическая индуктивность в зонах неустойчивости
На рис. 3 приведена осциллограмма процесса возбуждения и
затухания параметрических колебаний во II зоне неустойчивости, полученные при развертке осциллографа в 2 мс (верхний
сигнал – напряжение в резонансном контуре, нижний – ток).
Рис. 3. Возбуждение и затухание параметрических колебаний
Международная IEEE-Сибирская конференция по управлению и связи (SIBCON-2011)
Если нарастание колебаний в системе происходит по экспоненциальному закону (при выполнении условия возбуждения), то длительность гашения колебаний всецело зависит от
энергетических запасов системы и величины потерь [4], [5].
На рис. 4 приведены осциллограммы магнитной проницаемости и внешний вид параметрических колебаний в системе,
построенной на ферритовых сердечниках М1500 НМ 5х3х2,5 с
ёмкостью резонансного контура 0,1 мкФ, на частоте возбуждения 6,5 кГц, в зависимости от зоны неустойчивости. Осциллограммы получены на осциллографе С1-83 с временем развертки Т = 50 мс и амплитудой 0,5 В/дел. Рисунок наглядно иллюстрирует, что с ростом интенсивности воздействия увеличивается время, при котором индуктивность в системе минимальна,
то есть точка фазового перехода параметрических колебаний
смещается от края характеристики. Причем максимальные
значения индуктивности имеют место при относительно постоянной величине намагничивания.
Рис. 4. Магнитная проницаемость и вид нелинейных параметрических
колебаний в высших зонах неустойчивости
Следовательно, увеличение интенсивности воздействия
(накачки) приводит к увеличению степени нелинейности системы при относительно постоянной величине потерь. Эта зависимость раскрывает механизм возбуждения параметрических колебаний в высших зонах неустойчивости [1], [2], [4], [5]. При
переходе системы из одной зоны в другую путём изменения частоты воздействия, крутизна нелинейной характеристики остается практически постоянной. При этом максимум магнитной проницаемости, при переходе от высших зон к низшим зонам
асимптотически приближается к её величине в I зоне неустойчивости.
На рис. 5 представлены осциллограммы магнитной проницаемости с амплитудой развертки 20 мВ/дел при Iн=20мА
для II, IV, VI и XV зоны. Для таких систем характерны: режим жесткого возбуждения колебаний и явление затягивания
их амплитуды при изменении интенсивности накачки.
2
Рис.5. Изменение магнитной проницаемости
На рис. 6 приведены амплитудные характеристики колебаний в исследуемом параметрическом генераторе для первых
трех зон неустойчивости. Кривой 1 соответствует система без
потерь, кривой 2 – при сопротивлении в резонансном контуре
10 Ом, кривой 3 – при 20 Ом и кривой 4 – при 30 Ом.
Рис. 6. Амплитудные характеристики колебаний
в параметрическом генераторе с потерями
Режим жёсткого возбуждения параметрических колебаний
возможно получить также при изменении частоты воздействия, в
случае преобладания в реактивном сопротивлении контура ёмкостной компоненты. На рис. 7 приведена АЧХ параметрического генератора, выполненного на сердечниках из феррита
1500НМ 752 с обмотками: W1=26, W2 =50 витков и ёмкостью в
контуре С=0,1мкФ, при амплитуде накачки U Í =3В для первых
трёх зон параметрического возбуждения. Кривой 1 соответствует
система без потерь, кривой 2 – c сопротивлением в резонансном
контуре 10 Ом, кривой 3 – c сопротивлением 20 Ом.
Из представленных графических зависимостей очевидно, что
при малых потерях ограничение амплитуды колебаний происходит за счет изменения степени нелинейности системы.
Рис. 7. АЧХ параметрического генератора с потерями
На рис. 8 представлены характеристики колебаний исследуемого параметрического генератора во II зоне неустойчивости. На рис. 8, а, кривым 1–3 соответствуют АЧХ системы при
емкости в контуре 0,2 мкФ, 0,3 мкФ и 0,4 мкФ. На рис. 8 б,
показана зависимость амплитуды параметрических колебаний
от величины ёмкости в резонансном контуре при различных
интенсивностях накачки: кривой 1 соответствует Uн = 0,85В;
кривой 2 – 0,9В; кривой 3 – 0,95В; кривой 4 – 1В.
Международная IEEE-Сибирская конференция по управлению и связи (SIBCON-2011)
а)
б)
Рис. 8. Амплитудные зависимости колебаний параметрического генератора
Из представленных графических зависимостей очевидно,
что на определенной частоте возбуждения имеется оптимальное значение ёмкости контура, при котором добротность системы максимальна. Увеличение интенсивности воздействия
приводит к увеличению модуляции параметра системы и
уменьшению её средней индуктивности, что вызывает расстройку контура. Увеличение расстройки ведет к резкому падению амплитуды колебаний системы [6], [7].
На рис. 9 показана связь тока накачки iн (верхний график)
с характером возбуждения параметрического генератора,
выполненного на сердечниках из феррита 1500НМ 752 с
обмотками: W1=26, W2=50 витков и ёмкостью в контуре
С=0,1мкФ, для первых трёх зон неустойчивости (нижний
график). Из рис. 9 следует, что наибольший отбор энергии
система осуществляет внутри зоны неустойчивости на отрезке прироста амплитуды параметрических колебаний. В области максимума амплитуды колебаний и в зоне устойчивости
потребления системы снижаются [6], [7].
При исследованиях асимметричных систем экспериментально было установлено, что при значительном изменении числа
витков (практически до 40) возможно возбуждение колебаний
в системе в тех же зонах неустойчивости, что и при симметрии
системы. Но при этом пороговые характеристики колебаний
зависят как от интенсивности воздействия (накачки), так и неидентичности числа витков . Чем больше величина  в резонансном контуре, тем ниже и левее проходят пороговые характеристики. Наличие неидентичности числа витков обмотки  обусловливает необходимость увеличения интенсивности воздействия (накачки) для возбуждения параметрических колебаний в
соответствующих зонах неустойчивости [4], [5].
Рис. 9. Связь энергопотребления системы с характером ее возбуждения
3
колебаний Рн и паразитной мощности Рр, от неидентичности числа витков 
контура возбуждения для I–IV зоны неустойчивости (а) и зависимость
напряжения разбаланса от разницы в витках обмоток (б)
На рис. 10, а, приведены зависимости мощности возбуждения параметрических колебаний Рн (количество энергии резонансного контура, обусловленной параметрическим эффектом) и
паразитной мощности Рр, вызванной асимметрией системы
(энергия, полученная внешним «силовым» воздействием), от
неидентичности числа витков  контура возбуждения для I–IV
зоны неустойчивости (соответственно кривые 1–4). Из графика
следует, что с увеличением значения  мощность Рн увеличивается, но при этом параметрический резонанс наблюдается во
всех зонах неустойчивости. Это объясняется тем, что напряженность поля создаваемого в I и II сердечниках равны, но магнитная индукция в сердечнике с бóльшим числом витков достигает
значения индукции насыщения быстрее, чем в другом [1], [2].
При достижении в одном сердечнике индукции насыщения
индуктивность его обмотки уменьшается, и значительное напряжение источника накачки окажется приложенным к обмотке
ненасыщенного сердечника. Возрастание тока в обмотке второго
сердечника приводит к увеличению в нем напряженности магнитного поля и, соответственно, магнитная индукция в нем будет
стремиться к индукции насыщения. Но при этом, в резонансном
контуре увеличивается ток разбаланса (как результат прямого
«силового» воздействия), что ведет к увеличению в нем паразитной мощности Рр (на рис. 10, а, кривые Рр = f() показаны пунктиром). Очевидно, что нормальный режим возбуждения системы
обеспечивается при разнице в витках до 20.
Дальнейшее увеличение  приводит к значительному росту подводимой энергии. При введении одновременно рассогласованных характеристик ,  и  для параметрического
возбуждения системы необходимо прикладывать воздействие
гораздо большей интенсивности. Резонансные кривые, как и
для всякой нелинейной колебательной системы, при малых
значениях потерь имели скачки амплитуды с одной устойчивой ветви на другую. При увеличении потерь система работала в режиме, близком к линейному.
Зависимость напряжения разбаланса от разницы в витках обмоток Up=f() изображена на рис. 10, б. Как видно из
графика, напряжение разбаланса резко возрастает при
20%, что приводит к уменьшению прироста энергии системы обусловленной параметрическим эффектом.
На рис. 11 показано изменение тока в резонансном контуре
при наличии неидентичности витков и изменении тока накачки
iк = f(iн). Асимметрия вызывает необходимость увеличения тока
iн для получения требуемой модуляции индуктивности, что
ведет к увеличению iк. Это снижает усилительные свойства
системы, т.к. флуктуации тока в резонансном контуре, которые
должны быть усилены, будут во много раз меньше токов разбаланса. Чувствительность системы уменьшается [4] – [6].
Рис. 11. Изменение тока резонансной системы
а)
б)
Рис. 10. Зависимость мощности возбуждения параметрических
Полученные результаты показывают, что доля энергии, переданная в параметрическую систему благодаря прямому «силовому» воздействию (не параметрическому), определяется
величиной неидентичности ее структуры. При проектировании
Международная IEEE-Сибирская конференция по управлению и связи (SIBCON-2011)
режима колебаний такой нелинейной системы, наряду с потерями и параметрами существующих в резонансном контуре
колебаний необходимо учитывать степень ее асимметрии.
На рис. 12, a, представлена АЧХ параметрического генератора, выполненного на сердечниках из феррита 1500НМ 752 с
обмотками: W1=26, W2 =50 витков и ёмкостью в контуре С=0,1
мкФ, при накачке 3,25 В для первых трех зон неустойчивости.
Кривая 1 соответствует симметричной системе, кривая 2 –
системе с неидентичностью в витках вторичной обмотки =4%,
кривая 3 – с неидентичностью =8%. На рис. 12, б, показана
АЧХ того же параметрического генератора, но с ёмкостью в
резонансном контуре С=0,47 мкФ, при накачке 2,5 В.
a)
б)
Рис. 12. АЧХ асимметричной системы
Кривая 1 соответствует симметричной системе, кривая 2 –
системе с неидентичностью в витках вторичной обмотки =4%,
кривая 3 – с неидентичностью =10%. Анализ полученных
результатов показал, что наличие асимметрии витков вторичной обмотки приводит к расширению зоны неустойчивости
колебаний. Чем больше величина , тем ниже и правее по частотной оси проходят пороговые характеристики, то есть система возбуждается на более высоких частотах.
На рис. 13 приведены амплитудные характеристики колебаний в I и II зонах неустойчивости для таких же вариантов
конструкции генератора: рис. 13, а – на частоте возбуждения
20 кГц, рис. 13, б – на частоте 8,5кГц. Нумерация кривых на
графиках соответствует случаям, описанным выше.
4
зоне возбуждения ниже, чем во второй зоне. В асимметричной системе разница между максимумами амплитуд колебаний в зонах неустойчивости меньше. Представленные зависимости (рис. 11 – 13) соответствуют жёсткому режиму
возбуждения колебаний в НПС при изменении частоты и
мягкому режиму – при изменении амплитуды воздействия.
III. ЗАКЛЮЧЕНИЕ
Экспериментальные исследования свидетельствуют о том,
что асимметрия системы вызывает не только расширение области неустойчивости, а и увеличение амплитуды колебаний в характерных точках. Расширение зон неустойчивости колебаний
приводит к сужению (при значительной асимметрии к полному
отсутствию) областей, где нет колебаний (зоны устойчивости).
При этом переходы из зоны в зону происходят скачком без значительного изменения амплитуды колебаний в резонансном контуре. Данный факт отрицательно сказывается на усилительных
свойствах системы и ее частотной избирательности.
Проведенные исследования влияния других факторов неидентичности параметрического генератора (, , , ) и их комбинаций имели сходные результаты. При значительной степени
асимметрии системы (практически от 25%), вызывающей снижение ее собственной частоты, порядок следования пороговых
характеристик возбуждения при изменении частоты менялся [9].
Анализ полученных результатов показывает, что колебания в асимметричной системе имеют широкий спектр
гармоник, который вместе с флуктуациями является вынуждающей силой для возбуждения колебаний. Гармоники способствуют возбуждению и стабилизации колебаний.
Накачка оказывает влияние на АЧХ системы, обусловленное внесением дополнительной расстройки. Во всех случаях неидентичности характерным является расширение
области неустойчивости. Полученные экспериментальные
результаты подтверждают выводы, сделанные в предыдущих публикациях [1]–[7].
ССЫЛКИ НА ЛИТЕРАТУРУ
[1]
a)
б)
Рис. 13. Амплитудная характеристика асимметричной системы
[2]
Наличие неидентичности витков вторичной обмотки и в
этом случае приводит к расширению зоны неустойчивости
колебаний. Чем больше величина , тем ниже и левее проходят пороговые характеристики возбуждения. При этом система возбуждается при меньшей модуляции реактивности.
Асимметрия системы обусловливает наличие в резонансном
контуре токов, являющихся следствием прямого «силового»
воздействия, которые усиливаются и служат источником
ударного параметрического возбуждения колебаний в контуре. Это объясняет факт смещения АЧХ асимметричной параметрической системы в область более высоких частот.
На рис. 13, б хорошо заметно влияние добротности нелинейной системы на амплитуду возбуждаемых в ней параметрических колебаний. На частоте первой зоны неустойчивости
резонансный контур имеет меньшую добротность по сравнению с высшей зоной, поэтому амплитуда колебаний в первой
[3]
[4]
[5]
[6]
[7]
П.И. Чередников, “Расчёт и проектирование параметрических систем на
высших гармониках”, Опубл. в изд. Харьковского Нац. Универс. радиоэлектроники, Украина, 1980, – 98 с. (монография).
Л.В. Черкесова, О.И. Подгайко “Моделирование нелинейно-параметрических систем”. – Новочеркасск: Опубл. в редакции “Изв. вузов. Электромеханика”. – 2006. – 244 с. (монография).
Л.В. Черкесова, “Построение и анализ математической модели нелинейных процессов в параметрическом резонаторе при асимметрии
его внутренней структуры и гармоническом внешнем воздействии”.
Опубл. в журнале “Успехи современной радиоэлектроники”. Изд.
«Радиотехника», г. Москва, 2009. № 8. С. 16 – 28.
Л..В. Черкесова, “Построение математической модели и анализ энергетических процессов сильно асимметричного нелинейного параметрического
зонного резонатора при полигармоническом внешнем воздействии”.
Опубл. в журн. “Успехи современной радиоэлектроники”. Изд. «Радиотехника», г. Москва, 2010. № 1. С. 5 – 19.
Л.В. Черкесова, “Зависимость амплитуды параметрических колебаний нелинейного резонатора от амплитуды и частоты накачки”, конф. Математ. методы
в технике и технологиях – ММТТ-23: сб. трудов XXIII Междунар. науч. конф. :
в 12 т. – Саратов: Саратовский Гос. техн. ун-т, 2010. – Т. 7, секц. 8. – С. 82 – 85.
Л.В. Черкесова, А.Н. Заиченко, “Влияние амплитуды и фазы внешнего
полигармонического воздействия на колебания системы”, конф. Студенческая весна – 2006: Сб. научн. тр. асп. и ст. ЮРГТУ (НПИ), Юж. – Рос. гос.
техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ (НПИ), 2006. – С. 225-227.
Л.В. Черкесова, А..Н. Заиченко, “Автоматизированная система визуализации
нелинейно-параметрических колебаний в высших зонах неустойчивости
Международная IEEE-Сибирская конференция по управлению и связи (SIBCON-2011)
NONLINEAR PARSYS”, Свид.-во об отрасл. регистр. разраб. в гос. координац. центре информ. технологий, ОФАП, № 7447, от 27.12. 2006 г.
Лариса Владимировна Черкесова (Член IEEE с 2011г.)
родилась в Харькове, Украина, 7 апреля 1965 г. Окончила с отличием (красный диплом) Харьковский институт радиоэлектроники им. акад. М.К. Янгеля в 1986г.
(сейчас – Харьковский национальный университет радиоэлектроники) с присвоенной квалификацией «Радиоинженер–системотехник», и аспирантуру того же университета по специальности
«Радиофизика». Кандидат технических наук в области моделирования радиоэлектронных систем (Харьков, 1996, диплом к.т.н. переаттестован в России в
1997 г.). С 1989 г. является сотрудником Новочеркасского политехнического
института (сейчас – Южно-Российский государственный технический университет) сначала в качестве ведущего инженера-электронщика Вычислительного
центра ЮРГТУ (НПИ), затем – ассистента, затем доцента кафедры «Информатика и вычислительная техника». В настоящее время - доцент кафедры «Информатика» (аттестат ВАК - 2001 г.), руководитель специальности «Информационные технологии в медиаиндустрии», докторант-соискатель физического
факультета Южного федерального университета, Ростов-на-Дону, по специальности «Радиофизика». Учёный секретарь факультета информационных
технологий и управления ЮРГТУ (НПИ).
Научные интересы: радиоэлектроника, радиофизика, математическое
моделирование телерадиосистем, синергетика, информационные технологии. Текущие исследования – моделирование резонансных колебательных систем – нелинейно-параметрических зонных систем в высших зонах
неустойчивости колебаний.
Александр Николаевич Заиченко – аспирантсоискатель, родился в Новочеркасске 16 декабря 1983
года. Окончил физико-математический факультет ЮжноРоссийского государственного технического университета
(Новочеркасского политехнического института). С 2006 г.
является ассистентом, а с 2007г. – аспирантом кафедры
«Информатика» факультета информационных технологий и управления
ЮРГТУ (НПИ). Научный руководитель – доц., к.т.н. Черкесова Л.В.
Научные интересы – математическое моделирование, радиоэлектроника,
радиофизика, программирование, компьютерная графика.
Larissa Vladimirovna Cherckesova (Member IEEE since
2011.) was born in Kharkov, Ukraine, on April, 7th, 1965.
Has graduated with first-class honours degree (the red
diploma) the Kharkov institute of radio electronics (by
name acad. M.K. Jangel) in 1986г. (Now - Kharkov National University of Radio
electronics) with the appropriated qualification of "Radio engineering - system engineering", and postgraduate study of the same university on speciality of "Radio
physicist". The Candidate of technical science in the field of modelling of radioelectronic systems (Kharkov, 1996, the diploma was nostrificated in Russia in 1997).
Since 1989 is the employee of Novocherkassk polytechnic institute (now - the South
Russian state technical university) at first as the leading engineer-electronics of
Computer centre of SRSTU (NPI), then - the assistant, then the senior lecturer of
chair «Computer science and computer facilities». Now - the senior lecturer of chair
"Computer science" (certificate Higher Attestation Commission in 2001). The leader
of speciality «Information technologies in the media industry», the doktorantcompetitor of physical faculty of Southern federal university (SFU), Rostov-on-Don,
on speciality of "Radio physicist". The scientific secretary of faculty of “Information
technologies and control” of SRSTU (NPI), Novocherkassk.
Scientific interests: radio electronics, radio physics, mathematical modelling of television and radio systems, synergetic, information technologies.
Current researches - modelling of resonant oscillatory systems – nonlinear
parametrical zone systems in the higher zones of instability of oscillations.
Alexander Nikolaevich Zaichenko – post-graduate student,
the competitor, was born in Novocherkassk, Russia, on December, 16-th, 1983. Has graduated physical-and- mathematical
faculty of the South Russian state technical university (Novocherkassk polytechnic institute).
Since 2006 is assistant, and with 2007 – post-graduate student of
chair "Computer science" of faculty of information technologies
and control of SRSTU (NPI). Scientific Supervisor – L.V. Cherckesova.
Scientific interests - mathematical modelling, radio electronics, radio physics,
programming, computer graphics, information technologies.
5