( +) Cos
реклама
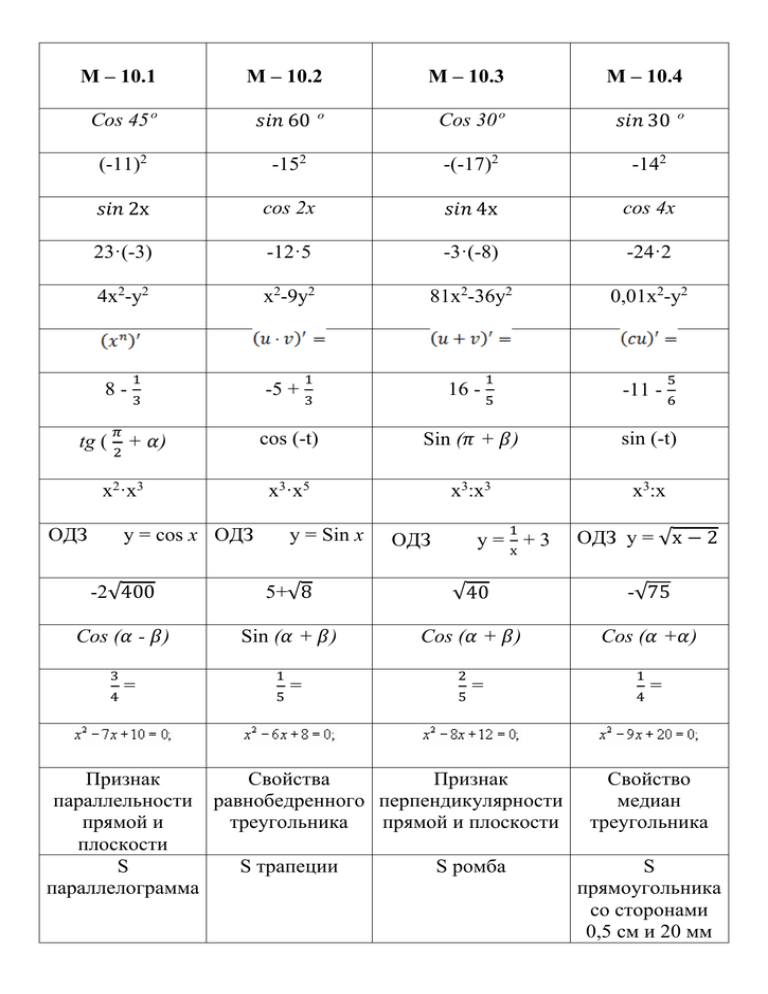
М – 10.1 М – 10.2 М – 10.3 М – 10.4 Cos 45º 𝑠𝑖𝑛 60 º Cos 30º 𝑠𝑖𝑛 30 º (-11)2 -152 -(-17)2 -142 𝑠𝑖𝑛 2х cos 2x 𝑠𝑖𝑛 4х cos 4x 23·(-3) -12·5 -3·(-8) -24·2 4х2-у2 х2-9у2 81х2-36у2 0,01х2-у2 8- 1 -5 + 3 𝜋 1 16 - 3 1 -11 - 5 5 6 tg ( + 𝛼) cos (-t) Sin (𝜋 + 𝛽) sin (-t) х2·х3 х3·х5 х3:х3 х3:х 2 ОДЗ у = cos x ОДЗ у = Sin x 1 ОДЗ у= +3 х ОДЗ у = √х − 2 -2√400 5+√8 √40 -√75 Cos (𝛼 - 𝛽) Sin (𝛼 + 𝛽) Cos (𝛼 + 𝛽) Cos (𝛼 +𝛼) 3 4 = 1 5 = 2 5 = 1 4 = Признак Свойства Признак Свойство параллельности равнобедренного перпендикулярности медиан прямой и треугольника прямой и плоскости треугольника плоскости S S трапеции S ромба S параллелограмма прямоугольника со сторонами 0,5 см и 20 мм М – 10.5 М – 10.6 М – 10.7 М – 10.8 𝑠𝑖𝑛 45º Cos 𝑠𝑖𝑛 90º Cos 1,22 -162 -(-18)2 -192 𝑠𝑖𝑛 х cos x tg 𝛼 ctg 𝛽 𝑠𝑖𝑛 2х cos 2x 12,5·8 -0,2·4,5 0,7·5000 0,24·0,5 4х2-25 (х-9)2 81х2-36у2 х2+4ху+4у2 ((4 – 8х)5)´ 2 16 - ( 3𝑠𝑖𝑛 х) ´ 2 9+ (7х4 + 6х – 3) ´ 3 -8 - 𝜋 Sin (𝜋 - 𝛼) 7 ctg ( - 𝛼) 2 х3·х-9 ОДЗ у = х−3 5 𝛱 4 2 х3:х-5 ОДЗ у = 5−у у 4 𝛱 3 (Cos2 x) ´ 4 12 7 Cos (𝜋 - 𝛼) х3:х-1 ОДЗ у = √х − 9 х4·х-5 ОДЗ у = 2х−3 (х−6)(х+7) √0,225 -2√2,56 5+√0,04 √361 sin 𝛼 + sin 𝛽 Cos 𝛼 - Cos 𝛽 sin 𝛼 - sin 𝛽 Cos 𝛼 + Cos 𝛽 13 26 = Свойства средней линии треугольника Площадь круга 15 25 = Теорема о трех перпендикулярах Площадь треугольника 12 15 = Вписанный угол 24 36 = Свойства касательных, проведенных к окружности из одной точки Длина окружности Площадь прямоугольного треугольника М – 10.9 М – 10.10 М – 10.11 𝑠𝑖𝑛 0 º Cos -1,22 (-1,6)2 -0,82 -(-1,9)2 tg 𝛼 ctg 𝛼 tg2 𝛼 + 1 ctg2 𝛼 + 1 sin2 t + cos2 t -125·8 -0,2·45 0,7·50 -0,16·0,5 9х2-121 (х-1)2 4х2-49у2 х2+6ху+9у2 ((4х – 8)3)´ ((7 – х)11)´ (√х)´ ( )´ tg 𝛱 2 12 -2 tg ( 𝜋 2 2 9+ 3 - 𝛼) 3 45 ctg(𝜋 - 𝛼) (х4)3 х3·х-6 ОДЗ у = 2х5+4х3 ОДЗ у = - √х 𝛱 𝑠𝑖𝑛180º 6 1 х 5 7Sin( М – 10.12 18 - 4 3𝜋 - 𝛼) 2 3𝜋 Cos ( х3:х-9 ОДЗ у= 2 4 7 + 𝛼) х3:х-3 1 √х ОДЗ у = tg х -2√64 5+√196 √121 -√144 Cos (𝛼 + 𝛽) Sin (𝛼 + 𝛽) sin 𝛼 + sin 𝛽 Cos (𝛼 - 𝛽) 48 96 = Вертикальные углы 15 60 = Признаки параллельности прямых 12 48 = Смежные углы Площадь Объем Периметр квадрата поверхности куба прямоугольного параллелепипеда 24 72 = Теорема косинусов Объем куба М – 10.13 𝑠𝑖𝑛 М – 10.14 𝛱 Cos 2 М – 10.15 𝛱 𝑠𝑖𝑛 2 𝛱 6 М – 10.16 tg 𝛱 6 0,12 -0,22 -(-0,5)2 1,72 2 𝑠𝑖𝑛 х cos x ctg2 𝛼 + 1 𝑠𝑖𝑛 4х cos 4x tg2 𝛼 + 1 -25·40 -2·3,05 -1,2·(-50) -1,3·8 4х2-225 (х-5)2 16х2-у2 х2+8ху+16у2 (2 𝑠𝑖𝑛 3 х)´ (2 𝑠𝑖𝑛 х cos x)´ (cos2 x)´ (sin2 t + cos2 t)´ 10 -2 Cos ( 3𝜋 2 2 6 7 + 𝛼) 11 3 -2 tg (𝜋 + 𝛼) х2·х-2 ОДЗ 3 7 -5 4 Sin( х3:х-10 у = 5 sin х ОДЗ 3𝜋 2 - 𝛼) х3:х-4 у = 2 - 6х ОДЗ у = х2 + 8 11 - 5 4 7 𝜋 ctg ( + 𝛼) 2 х4·х-6 ОДЗ у = -3Cosх -2√36 5+√81 √225 -√144 Sin (𝛼 - 𝛽) Cos (𝛼 + 𝛽) sin 𝛼 - sin 𝛽 Cos (𝛼 - 𝛽) 15 45 = Признаки равенства треугольников Площадь треугольника 16 48 = Теорема косинусов 22 77 = Признаки параллелограмма 14 32 = Теорема синусов Периметр Площадь кругового Площадь прямоугольника сектора прямоугольного треугольника М – 10.17 tg 𝛱 М – 10.18 𝑠𝑖𝑛 3 𝛱 4 М – 10.19 М – 10.20 Cos60º 𝑠𝑖𝑛 1 𝛱 3 0,022 -0, 013 (- )2 - ( -0,5)2 tg 𝛼 cos 2x 𝑠𝑖𝑛 4х 𝑠𝑖𝑛 х cos x -2,5 · 1000 4,8 : 0,24 -6,15 : 3 0,35 : (-7) 49х2-225 (х-8)2 81х2-36у2 х2+4ху+4у2 (2 𝑠𝑖𝑛 3 х)´ (√х)´ (cos2 x)´ ( )´ -7-5,1 -5+1,7 -400-26 6,5-2,8 Cos (𝜋 - 𝛼) Sin (𝜋 - 𝛼) tg ( + 𝛼) cos (-t) 75 % = 9%= 100 % = 0,1 % = ОДЗ у = 5−у у ОДЗ у= 3 1 √х 1 х 𝜋 2 ОДЗ у = - √х ОДЗ у = х2 + 8 √75 90 + √8 7- √0,04 √0,0225 Cos 𝛼 + Cos 𝛽 sin 𝛼 + sin 𝛽 Sin (𝛼 + 𝛽) Sin (𝛼 +𝛼) 48 96 = 24 72 = 12 48 = 16 48 = 5х – х2 =0 х + х2 =0 - х2 = -7 8 х2 =2 Признаки подобия треугольников Свойства параллельных прямых Неравенство треугольника Теорема косинусов Площадь треугольника Площадь ромба Площадь параллелограмма Площадь трапеции