Прямоугольный треугольник

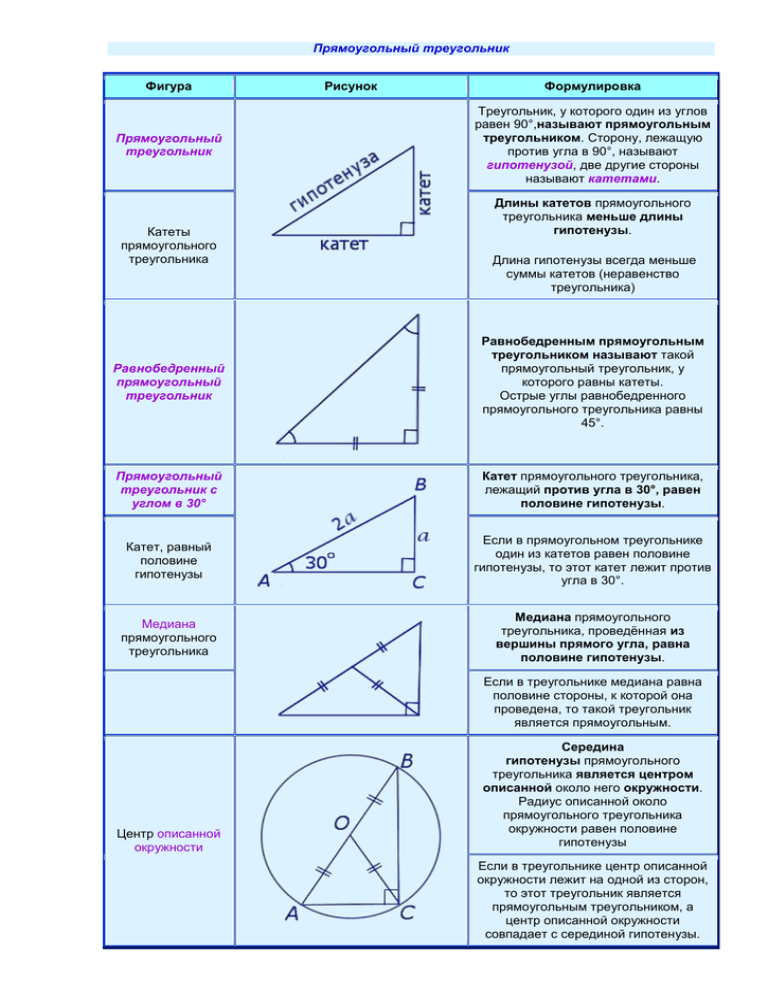
Прямоугольный треугольник
Фигура
Прямоугольный
треугольник
Катеты
прямоугольного
треугольника
Рисунок
Формулировка
Треугольник, у которого один из углов
равен 90°,называют прямоугольным
треугольником. Сторону, лежащую
против угла в 90°, называют
гипотенузой, две другие стороны
называют катетами.
Длины катетов прямоугольного
треугольника меньше длины
гипотенузы.
Длина гипотенузы всегда меньше
суммы катетов (неравенство
треугольника)
Равнобедренный
прямоугольный
треугольник
Равнобедренным прямоугольным
треугольником называют такой
прямоугольный треугольник, у
которого равны катеты.
Острые углы равнобедренного
прямоугольного треугольника равны
45°.
Прямоугольный
треугольник с
углом в 30°
Катет прямоугольного треугольника,
лежащий против угла в 30°, равен
половине гипотенузы.
Катет, равный
половине
гипотенузы
Если в прямоугольном треугольнике
один из катетов равен половине
гипотенузы, то этот катет лежит против
угла в 30°.
Медиана
прямоугольного
треугольника
Медиана прямоугольного
треугольника, проведённая из
вершины прямого угла, равна
половине гипотенузы.
Если в треугольнике медиана равна
половине стороны, к которой она
проведена, то такой треугольник
является прямоугольным.
Центр описанной
окружности
Середина
гипотенузы прямоугольного
треугольника является центром
описанной около него окружности.
Радиус описанной около
прямоугольного треугольника
окружности равен половине
гипотенузы
Если в треугольнике центр описанной
окружности лежит на одной из сторон,
то этот треугольник является
прямоугольным треугольником, а
центр описанной окружности
совпадает с серединой гипотенузы.
В прямоугольном
треугольнике квадрат гипотенузы
равен сумме квадратов катетов
Теорема Пифагора
c2 = a 2 + b 2
Если в треугольнике квадрат одной
стороны равен сумме квадратов двух
других сторон, то такой треугольник
является прямоугольным
Обратная
теорема
Пифагора
cos A = sin B,
Свойства
катетов
прямоугольного
треугольника
sin A = cos B
Катет прямоугольного треугольника
есть среднее пропорциональное
между гипотенузой и проекцией этого
катета на гипотенузу.
Высота прямоугольного треугольника,
проведенная из вершины прямого
угла, есть среднее пропорциональное
между проекциями катетов на
гипотенузу.
Свойства высот
прямоугольного
треугольника
Высота может быть найдена через
отношения произведения катетов на
гипотенузу
Признак равенства
прямоугольных
треугольников по
двум катетам
Если два катета одного
прямоугольного треугольника
соответственно равны двум катетам
другого прямоугольного треугольника,
то такие прямоугольные треугольники
равны
Признак равенства
прямоугольных
треугольников по
катету и
прилежащему
острому углу
Если катет и прилежащий к нему
острый угол одного прямоугольного
треугольника соответственно равны
катету и прилежащему к нему острому
углу другого прямоугольного
треугольника, то такие прямоугольные
треугольники равны
Признак равенства
прямоугольных
треугольников по
катету и
противолежащем
у острому углу
Если катет и противолежащий острый
угол одного прямоугольного
треугольника соответственно равны
катету и противолежащему острому
углу другого прямоугольного
треугольника, то такие прямоугольные
треугольники равны
Признак равенства
прямоугольных
треугольников по
гипотенузе и
острому углу
Если гипотенуза и острый угол одного
прямоугольного треугольника
соответственно равны гипотенузе и
острому углу другого прямоугольного
треугольника, то такие прямоугольные
треугольники равны
Признак подобия
прямоугольных
треугольников п
о двум катетам
Если два катета одного
прямоугольного треугольника
пропорциональны двум катетам
другого прямоугольного треугольника,
то такие прямоугольные треугольники
подобны.
Признак подобия
прямоугольных
треугольников п
о острому углу
Если острый угол одного
прямоугольного треугольника равен
острому углу другого прямоугольного
треугольника, то такие прямоугольные
треугольники подобны.
Признак подобия
прямоугольных
треугольников п
о гипотенузе и
катету
Если гипотенуза и катет одного
прямоугольного треугольника
пропорциональны гипотенузе и катету
другого прямоугольного треугольника,
то такие прямоугольные треугольники
подобны.
Радиус вписанной
в
прямоугольный
треугольник
окружности
S =
1
ab
2
S =
Площадь
прямоугольного
треугольника
1
с hc
2
S = de