Фундаментальные константы.

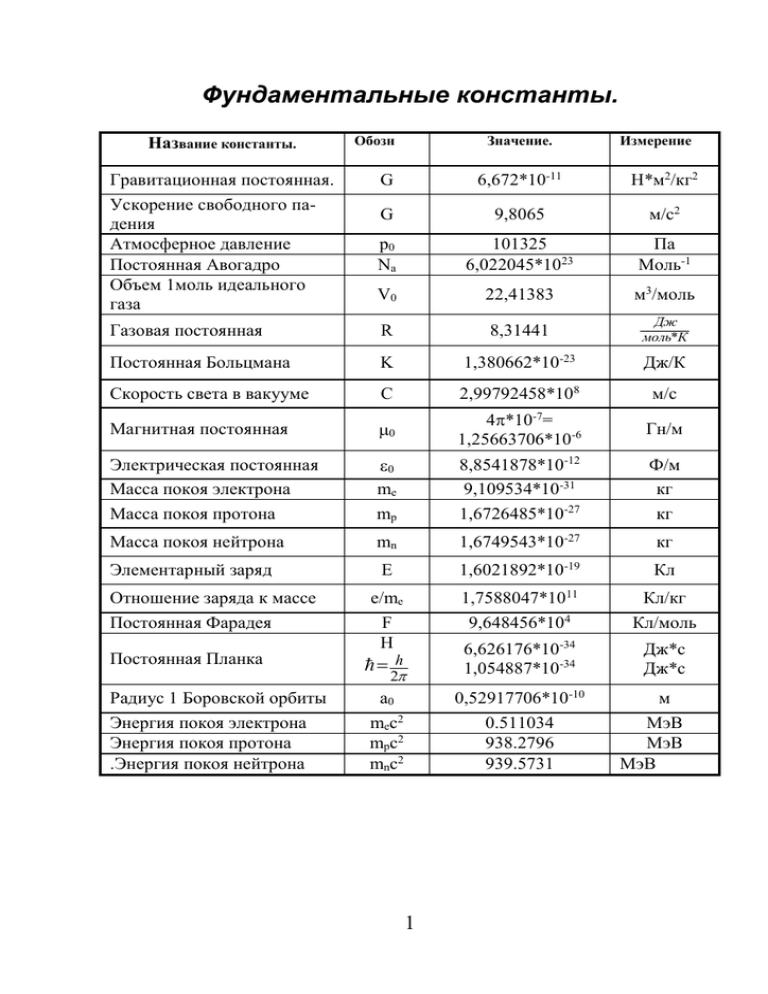
Фундаментальные константы.
Название константы.
Гравитационная постоянная.
Ускорение свободного падения
Атмосферное давление
Постоянная Авогадро
Объем 1моль идеального
газа
Обозн
Значение.
Измерение
G
6,672*10-11
Н*м2/кг2
G
9,8065
м/с2
p0
Na
101325
6,022045*1023
Па
Моль-1
V0
22,41383
м3/моль
Газовая постоянная
R
8,31441
Дж
моль*К
Постоянная Больцмана
K
1,380662*10-23
Скорость света в вакууме
C
2,99792458*10
8
-7
Дж/К
м/с
Магнитная постоянная
0
4*10 =
1,25663706*10-6
Гн/м
Электрическая постоянная
Масса покоя электрона
Масса покоя протона
0
me
mp
8,8541878*10-12
9,109534*10-31
1,6726485*10-27
Ф/м
кг
кг
Масса покоя нейтрона
mn
1,6749543*10-27
кг
-19
Кл
11
1,7588047*10
9,648456*104
Кл/кг
Кл/моль
6,626176*10-34
1,054887*10-34
Дж*с
Дж*с
Элементарный заряд
Отношение заряда к массе
Постоянная Фарадея
E
1,6021892*10
e/me
F
H
Постоянная Планка

Радиус 1 Боровской орбиты
Энергия покоя электрона
Энергия покоя протона
.Энергия покоя нейтрона
a0
mec2
mpc2
mnc2
h
2
0,52917706*10-10
0.511034
938.2796
939.5731
1
м
МэВ
МэВ
МэВ
Система единиц.
Приставки Си.
пристав.
экса
пета
тера
гига
Э
П
Т
Г
по
ря
д.
пристав.
18
15
12
9
мега
кило
гекто
дека
М
к
г
да
по
ря
д.
пристав.
6
3
2
1
деци
санти
милли
микро
д
с
м
мк
по
ря
до
к
Пристав.
-1
-2
-3
-6
Нано
пико
фемто
атто
порядок
н
п
ф
а
Механика
Кинематика
Обозн.
S
v
t
x
a
Изм.
м
м/с
с
м
м/с2
с-1
с
Гц
с-2
м

T


R
Смысл
пройденный путь
скорость
время
координата
ускорение
угловая скорость
период
частота
угловое ускорение
радиус
Скорость и ускорение:


 dr
 dS
, v
,
v
dt
dt

 dv
a
dt
Равномерное движение:
v  const
S  vt , x  x 0  vt ;
Равнопеременное движение:
a=const,
,
v  v0
v 2  v 02
v 2  v 02
at 2
; a
; S  v0t 
; S
;
a
t
2S
2
2a
v=v0+at; v  v 02  2aS ;
Движение под углом к горизонту:
Vx  cos V0 -скорость по оси ОХ
V y  sin V0 -скорость по оси ОУ

tmax  V0 sin
g
и tполн=2t - максимальное время подъема
S  0
и
2
sin 2
g
S=υxtполн -
расстояние
2
-9
-12
-15
-18
H  0 2sing 
2
2
- максимальная высота
Движение тела, брошенного горизонтально:
t
2h
g
;
X max  V0 t  V0
2h
g
;V
 V0  g 2 t 2
2
Криволинейное движение:


v  v  e
e
2
  

 v 
a  a e  en , a  a  an
R
en
Движение по окружности:
 
aц   * r  ; aцс
 VR ; aцс  w2 r ; aц   v
2
v2
4 2 R
 4 2 Rn 2
; aцс 
R
T2
2
Fцс  m VR  4 2 n 2 rm
aц 
n
T
2
w ;w
2 ; w  2n

v
2  d
 d

,  , 
; 
;
dt
dt
R
T
2 R
1
N
 

v   * r  , v 
; 
,  ;
t
T
T
1
T ;

3
Динамика и статика
Обозн.
F
P
a
m
v
p
g
Изм.
Н
кг*м/с
м/с2
кг
м/с
Н
м/с2
Смысл
сила
импульс
ускорение
масса
скорость
вес тела
ускорение свободного падения
E
Дж
энергия
A
Дж
работа
N
Вт=Дж/с
мощность
t
с
время
I
кг*м2
момент инерции
L
кг*м2/с
момент импульса
M
Н*м
момент силы
-1
с
угловая скорость

Первый закон Ньютона:
при  F  0  v  const.
Второй закон Ньютона.



 dP
 dm 

v , при m=const  F  ma
, F  ma 
F
dt
dt
Третий закон Ньютона.


F12  F21
Основной закон динамики для неинерциальных систем отчета.
ma=ma0+Fинерц ,где а- ускорение в неинерциальной а0- в
инерциальной системе отчета.
n
Скорость центра масс v ц.м. 
P
i 1
n
m
i 1
Закон всемирного тяготения
4
i
i
;
m1 m2
,
R2
m
g  G планеты - ускорение свободного падения на планете.
Rпланеты
FG
v  mпл G - первая космическая скорость.
υ1=7,9*103 м/с, υ2=11,2*103м/с.
Вес тела
p=mg - вес тела в покое.
p=m(g+a) - опора движется с ускорением вверх.
p=m(g-a) - опора движется с ускорением вниз.
p=m(g-v2/r) - движение по выпуклой траектории.
p=m(g+v2/r) - движение по вогнутой траектории.
Сила трения.

F N,
Закон Гука.
Fупр=–kx, - сила упругости деформированной пружины.
F

- механическое напряжение
s
  l / l0 - относительное продольное удлинение (сжатие)
 ' = d / d 0 - относительное поперечное удлинение (сжатие)
'
  , где - коэффициент Пуассона.

Закон Гука:   E , где Е- модуль Юнга.
 Esl
F
l0
E 2
, кинетическая энергия упругорастянутого
Wкин  V
2
(сжатого) стержня. (V- объем тела)
5
Динамика и статика вращательного движения
 Fi  0 и  M i  0 условие равновесия тел
M=Fl, где l- плечо
F1l1=F2l2 уравнение статики


 dL
  dI
; M  I  
- момент силы
M
dt
dt


L  I - момент импульса
L=const - закон сохранения момента импульса.
I=I0+mb2 - теорема Штейнера
система
точка по окружности
стержень
стержень
шар
сфера
кольцо или тонкостенный цилиндр
диск сплошной цилиндр
ось
ось симметрии
через середину
через конец
через центр шара
через центр сферы
ось симметрии
ось симметрии
I
mR2
1
/12 mR2
1
/3 mR2
2
/5 mR2
2
/3 mR2
mR2
1
/2 mR2
Законы сохранения
Закон сохранения импульса
Неупругое взаимодействие:
m1 v1  m1 v 2  m1 v1  m2 v 2
'
'
m1v1  m2 v 2  m1v1  m2 v2
'
'
-в проекции на ось ОХ
Упругое соударение:
m1v1  m2 v2  (m1  m2 )v
m1v1  m2 v2  (m1  m2 )v
P=mv; - импульс тела.
Импульс силы:
-в проекции на ось ОХ
Ft  mv  mv0 ; Ft  P2  P1
или Ft=P
F  0
Реактивное движение:
m рак. v рак.  mоб. vоб.  m2 v2
m2 v2
6
- импульс газов
Потенциальная и кинетическая энергия. Мощность
 
A  F  S  cos  - работа силы F
A=E=Nt
dA FS
E
N

 F 
- мощность
dt
t
t
mv 2
- кинетическая энергия
Eкин 
2
mv 2 I 2
- кинетическая энергия вращательного движеEкин 

2
2
ния.
Ep=mgh - потенциальная энергия поднятого над землей тела.
kx 2
- потенциальная энергия пружины
Ep 
2
Закон сохранения энергии.
Eк1+Eр1=Eк2+Eр2
Молекулярная физика. Свойства газов и жидкостей.
Обозн.
p
V
T
N
m


U
Q
Изм.
Па
м3
К
–
кг
кг/Моль
Моль
Дж
Дж
Смысл
давление
объем
температура
число молекул
масса
молярная масса
кол-во вещества
вн. энергия газа
кол-во теплоты
7
–
КПД

уравнение Менделеева- Клайперона
N   NА, N 
m
m0
C
Дж/(кг*К)
λ
Дж/кг

pV=NkT -
m

Удельная теплоемкость
Удельная теплота
плавления
i
Nkt ,
2
i
U  pV - полная
2
U
внутренняя энергия истемы.
Число атомов
1
2
3
2 
3RT

i
 
3
7
13 (12)
;   mN a ;  
i2
i
5/3
9/7
15/13 (7/6)
N
m
N

;n 
V
M Na
p  13 m0 nv 2 - основное уравнение МКТ
p   pi - закон Дальтона для давления смеси газов.
m 2
1
2
i
kT  0 ; P  nkT   2  n E k
3
3
2
2
pV
 const
при N=const 
T
T=const изотерма PV=const закон Бойля-Мариотта
p=const изобара
V/T=const закон Гей-Люсака
V=const изохора
p/T=const закон Шарля
E
Броуновское движение.
v2 
3kT
среднеквадратичная скорость молекул.
m0
v  2kT / m0 - наиболее вероятная скорость молекул.
8
v
8 kT
- средняя арифметическая скорость молекул.
 m0
3/ 2
2
 m0 v
 m0 
f ( v )  4 
 v 2 e 2 kT - Закон Максвелла для рас 2 kT 
пределения молекул идеального газа по скоростям.
Среднее число соударений молекулы за 1с: z  2 d 2 n v
Средняя длинна свободного пробега молекул
1
l 
2 d 2 n
vt
r 
- средний путь молекулы за время t.
n 2 d 2
Распределение в потенциальном поле.
ph  p0 e
nh  n0 e
 mgh
kT
 mgh
kT
- барометрическая формула.
- распределение Больцмана.
Термодинамика
Q  A  U - первое начало термодинамики.
A  pV - работа газа.
Изотермический
p1 T1
pV  const или T  const

p 2 T2
A  NkT ln VV12
A  p1V1 ln
C Mr,T 
p1
p2
A

T
9
U  0 ; Q  A
Изобарный
V
 const или p  const
T
V1 T1
 ; U=Q+pV
V2 T2
A  pV  RT
3
pV
RT  
2
 1
3
C Mr , p  C Mr ,V  R ; C Mr , P  R  R
2
Изохорный
p1 T1
NkT
; Q  U 
; A0

V  const
 1
p 2 T2
Q  A  U  pV 
3m
RT
2M
3
C MrV  R
2
U
Адиабатный
Q
Q  0 C Mr ,Q 
 0 U  A
T
V  p  const - уравнение адиабаты.
Теплоемкость C 
C
Q
T
C удел н
dQ
dT
C

m
C Mr  C удел н Mr
Тепловой баланс
10
Qотд=Qполуч
Q  cm(t 2  t1 )  cmT - теплота на нагрев (охлаждение)
Q=rm - теплота парообразования
Q=-rm - теплота конденсации
Q=m - плавление
Q=-m - кристаллизация
Q=qm - сгорание.
Q1  Q2  Q3  0
Тепловое расширение.
l=l0(1+T ) линейное расширение
V=V0(1+T) объемное расширение
Тепловые машины.
Aïîëí
- коэффициент полезного действия
Q1
Q  Q2
T  T2
 1
,  max  1
Q1
T1

Гидростатика, гидродинамика.
Обозн.
p
V
m

v
S

h
Изм.
Па
м3
кг
Н/м
м/с
м2
кг/м3
м
at 2
S  v0t  ,
2
S  vt -
Смысл
давление
объем
масса
коэффициент поверхностного натяжения
скорость жидкости
площадь
плотность
высота столба жидкости.
p  gh (давление на глубине h).
плотность.
11
FA  g жидVтела ( сила Архимеда ).
F1 F2

- (гидравлический пресс).
S1 S 2
h  const - закон сообщающихся сосудов.
Sv  const - уравнение неразрывности.
v 2
 gh  p  const
2

p1  p 2  ( 22  12 )
2
- уравнение Бернулли
v 2
- динамическое,
2
р - статическое,
gh - гидростатическое давление.
FA  mg  плвает
FA  mg  тонет
 ж   тела  плавает
 ж   тела  тонет
E п.н.  S
F•.’.  l
- сила и энергия поверхностного натя-
жения.
h
2
- высота подъема жидкости в капилляре.
gr
  2 gh -формула Торичелли
Электрические и электромагнитные явления
Электростатика
Обозн.
F
q
E
U
Изм.
Н
Кл
н/Кл в/м
В
Смысл
Сила
Заряд
Напряженность
Напряжение
12
φ
C
I
R
A
N
B
L
В
Ф
А
Ом
Дж
Вт
Тл
Гн
FK 
E
q1  q2
1

4 0
r2
Потенциал
Электроемкость
Сила тока
Электрич сопротивление
Работа
Мощность
Магнтитн индукция
Индуктивность
- закон Кулона.
q
1
F


 2
, E
4 0 r
q 2 0
- напряженность электрического
поля


E   Ei - принцип суперпозиции полей.
 
Ф  E  S - поток через площадку S.
   qвнут р
E
- теорема Гаусса.
S  dS   0
 E  dl  0 - теорема о циркуляции.
L

 
W
,     E  dr - потенциал.
q
плоскость
сфера
шар


2 0


x
2 0
, при r < R
0
 2
   R
  r 2 , при r  R
 0
 R
  , при r < R

0


R

, при r  R
  0 r
 r
 3 , при r < R
 0

3
 R , при r  R
2
 3r  0
 (3R 2  r 2 )
, при r < R

6 0


3
 R , при r  R
 3r 0
13
цилиндр (пустой)
, при r < R
0

 
 2 r , при r  R
0

B
A  q  E  dl , A  q(1   2 )  IUt  I 2 Rt 
A
U  1   2 ,
C
q

U
A
,
q
U2
t
R
U  Ed
- электроемкость уединенного проводника.
 0 S
q
qU CU 2 q 2
C , C
, W
плоский кон

U
d
2
2
2C
денсатор.
C  4 0 r - электроемкость заряженного шара.
rr
C  4 0 1 2
- электроемкость сферического конденr2  r1
сатора.
1
1

Спа р ал   Сi
- батарея конденсаторов.
Спослед
Сi
p=qd - дипольный момент.
 pi поляризованность диэлектрика.
P
V
P=ж0E где ж- диэлектрическая восприимчивость.
E
=1+ж  
где - диэлектрическая проницаемость.
E вак
 Eds 
q
связ
0
- теорема Гаусса для диэлектриков.
Электродинамика. Постоянный ток.
I
q
,
t
I  qnSv ,
j
I
 qnv
S
14
U

E
, I
, j   E
R
Rr

l
R   ; R  R0 (1  T )
S
Aст


, Aст  It , I к .з . 
r
q
I
Закон Ома.
U2
t - закон Джоуля–Ленца.
R
dA
U2
E2
2
2
  E 
 jE
P
 IU  I R 

dt
R
Q  A  IUt  I 2 Rt 
 I  0 - правило Кирхгофа для узлов.
 I R    - правило Кирхгофа для контуров.
i
i
i
k
Параллельное соединение проводников:
I=const,
r   ri
U  U i
  i
R   Ri
1
1

c
ci
1
1
q  const

r
ri
Последовательное соединение:
I   Ii ,
U=const,

r
1
1

R
Ri

i
ri
c   ci
Законы электролиза.
q   qi
m  kq  kTI - первый закон Фарадея.

k
- второй закон Фарадея.
neN A
F
C
Na
15
Fлор
Электромагнетизм.
 
 q v * B , Fл  Bqv - сила Лоренца.


FА  BIl - сила Ампера, действующая на проводник длиной
l.
 

  0 q v * r 
v*E
, B
B

c2
4
r3
  I
B  0 (cos 1  cos  2 ) магнитная индукция поля в точке.
2b
 0 I
B
- магнитная индукция в центре витка.
2R

N
B  0 I
- индукция внутри соленоида.
l
  0 2 I
B

индукция поля проводника на расстоянии R от оси.
4 R
 
 
BdS

0
Bdl

   0  Iвнутр

B   0 H связь между магнитной индукцией и напряженностью


магнитного поля.


B   Bi
- принцип суперпозиции магнитных полей.
II
F   0 1 2 - сила взаимодействия двух проводников.
2R
 
Ô  BdS  BS cos - магнитный поток.
LI 2
- энергия магнитного поля.
Wм.п. 
2
Ф
L
I
dФ
i  
ЭДС индукции в замкнутом контуре.
dt
dI
 is   L
ЭДС самоиндукции.
dt
16
Колебания и волны. Оптика. Акустика.
Механические и электромагнитные колебания.
x  A sin( 0 t   ) - уравнение гармонических колебаний.
v  A0 cos(0 t   ) , a   A 02 sin(  0 t   )   02 x
E  12 mA2 20 - полная энергия колеблющейся точки.
2
T
; F  ma  m 2 x

Система.
Математический маятник.
Пружинный маятник.
Физический маятник.
Колебательный контур.
Период
Цикл. частота
Уравнение
g
    0

l
k

x x0
m
l
T  2
g

g
l
T  2
m
g

g
m
T  2
I
mgb

mgb
I
 

mgb
0
I

1
LC
q 
1
q0
LC
T  2 LC
Сложение колебаний.
A2  A12  A22  2 A1 A2 cos( 2  1 ) , при 1=2
x  x1  x 2  x m1e i1t  x m2 e i 2t  x m1e i1t (1 
2
- период пульсации.

1
k
  T ;   ;  
T
m
T
Затухающие колебания.
  i   0 ,  0   2  2
x  x me  t e   0t
 t
q  q0 e e
t
R2 1

4 L LC
17
x m2 it
e )
x m1
Переменный ток. Индуктивность и емкость в цепи переменного
тока.
i  I m cos t
U L  U m cos(t 

2
) - мгновенное значение напряжения на катуш-
ке
U m  I m L и U m 
Im
C
- амплитуда колебаний напряжения
Um
 L - индуктивное сопротивление
Im

U c  U m cos(t  ) - мгновенное значение напряжения на конден2
XL 
саторе
Xc 
Um
1
- емкостное сопротивление

I m C
I действ 
Im
,
2
U действ 
Um
- действующие значения силы тока
2
и напряжения
Z  R 2  (L 
N  U m I m cos 
1
) - импеданс
C
Упругие волны.
Скорость волны в газе: с  
kT
,
m0
Скорость волны в твердом теле: с 
E

  vT , v  
уравнение плоской волны: ( x, t )  A cos(t  kx   0 )
Отражение
 пад   отр
v  const
18
sin  пад
с
 2
sin  п р ел с1
Преломление
=0
lim пад=arcsin(c2/c1)
r1r2

, C  4 0 r  r
2
2
1
x  A1 cos(t  kx1 )  A2 cos(t  kx )

d
фазовая v и групповая u скорости: v = , u 
,
k
dt
dv
uv
d
Интерференция:  max  2 m

v  v
v  v
п р ием
исто 
  - эффект Доплера.

0
Электромагнитные волны.
v
1
1


 0 0

E  0   H  0
Отражение
Преломление
с
- фазовая скорость

 пад   отр
, при 1   2
  
0, при 1  2
sin  пад
с
 2
sin  п р ел с1
=0
lim пад=arcsin(c2/c1)
Оптика
  n1 x1  n2 x 2 - разность хода.
c
v=
- скорость света в среде
n
sin  пад n2
- закон преломления.

sin  отр n1
1 1 1
   Д - формула линзы.
f d F
h
f
K 
- увеличение линзы.
H d
19
Квантовая физика и теория относительности.
E  h - энергия фотона. h- постоянная Планка
mv 2
- фотоэффект
h  Aвых 
2
mv 2
- полная энергия.
E  m0 c 2 
2
2
m  m0 / 1  vc2
2
t '  t / 1  vc2
2
l  l0 1  vc 2
S 2  c 2 t 2  l 2  inv
Атомная физика
.
4 0  2 n 2
n2
rn 
 a0
mZe 2
Z
N  N0  2

t
T
- закон распада
20