Решения второй части
реклама
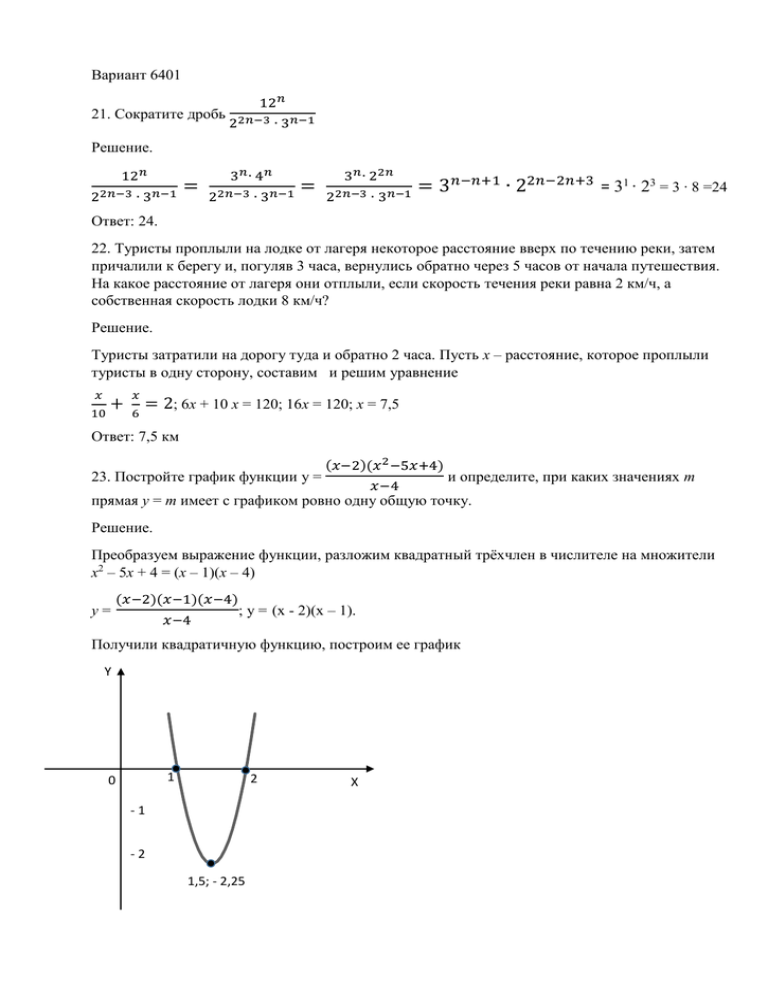
Вариант 6401 21. Сократите дробь 12𝑛 22𝑛−3 ∙ 3𝑛−1 Решение. 12𝑛 22𝑛−3 ∙ 3𝑛−1 = 3𝑛 ∙ 4 𝑛 22𝑛−3 ∙ 3𝑛−1 = 3𝑛 ∙ 22𝑛 22𝑛−3 ∙ 3𝑛−1 = 3𝑛−𝑛+1 ∙ 22𝑛−2𝑛+3 = 31 ∙ 23 = 3 ∙ 8 =24 Ответ: 24. 22. Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 5 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 8 км/ч? Решение. Туристы затратили на дорогу туда и обратно 2 часа. Пусть х – расстояние, которое проплыли туристы в одну сторону, составим и решим уравнение 𝑥 10 + 𝑥 6 = 2; 6х + 10 х = 120; 16х = 120; х = 7,5 Ответ: 7,5 км 23. Постройте график функции y = (𝑥−2)(𝑥 2 −5𝑥+4) и определите, при каких значениях m 𝑥−4 прямая y = m имеет с графиком ровно одну общую точку. Решение. Преобразуем выражение функции, разложим квадратный трёхчлен в числителе на множители х2 – 5х + 4 = (х – 1)(х – 4) y= (𝑥−2)(𝑥−1)(𝑥−4) ; y = (x - 2)(x – 1). 𝑥−4 Получили квадратичную функцию, построим ее график Y 1 0 2 -1 -2 1,5; - 2,25 X прямая y = m будет иметь одну общую точку с графиком функции при трех значениях m. Первый случай, когда прямая касается вершины параболы, т.е. при m = -2,25. Второй случай, когда прямая пересекает параболу в точке x = 1. Подставляя это х в параболу получаем y = m = 0. Третий случай, когда прямая пересекает параболу в точке x = 2. Подставляя это х в параболу получаем y = m = 0. Ответ: -2,25; 0 24. В прямоугольном треугольнике ABC с прямым углом С известны катеты: АС = 8, ВС = 15. Найдите медиану СМ. Решение. В М С А Медиана из прямого угла на гипотенузу равна половине гипотенузы (радиусу описанной окружности около данного треугольника). Гипотенуза равна корню квадратному из 8*8+15*15 = 289 или 17 см. Отсюда медиана 1/2 *17 = 8,5 Ответ: 8,5. 25. В параллелограмме ABCD точка Е – середина стороны CD. Известно, что ЕА = ЕВ. Докажите, что данный параллелограмм – четырехугольник. Решение. B C E А D Проведем дополнительное построение, диагонали AC и BD. Треугольники AED и BEC равны (CE и ED, EA и EB (по условию), CB и AD (свойство)), значит соответствующие углы равны, т.е. DEA = CEB. Треугольник BED = CEA(CE и ED, EA и EB (условие), угол BEA общий, DEA = CEB, значит BD = AC, которые являются диагоналями параллелограмма, значит ABCD прямоугольник. 26. Основание АС равнобедренного треугольника АВС равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности, вписанной в треугольник АВС. Решение. 1-й способ. Соединим центры окружностей - вписанной в треугольник АВС и вневписанной. Точку С также соединим с этими центрами. Угол КСО прямой, т.к. равен сумме половин смежных углов ( центры окружностей лежат на биссектрисах углов). Треугольник КСО - прямоугольный. СН в нем -высота и равна половине АС, т.е. равна 5 см. Отрезок ОН равен радиусу вневписанной окружности и равен 6 см. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Из этого следует равенство: СН² = ОН·КН; 25 = 6КН r =КН=25/6 = 4 1 6 2-й способ. Четырехугольники AHO1K и MAKO подобны, так как если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы (т. е. углы, лежащие между пропорциональными сторонами) этих многоугольников равны, то такие многоугольники подобны. 1 5 : r = 6 : 5; 6r = 25; r = 25/6 = 4 6 1 Ответ: 4 6 Вариант 6402 21. Сократите дробь 45𝑛 32𝑛−3 ∙ 5𝑛−1 Решение. 45𝑛 32𝑛−1 ∙ 5𝑛−2 = 9𝑛 ∙ 5 𝑛 32𝑛−1 ∙ 5𝑛−2 = 32𝑛 ∙ 5𝑛 32𝑛−1 ∙ 5𝑛−2 = 32n – 2n + 1 ∙ 5n –n + 2 = 31 ∙ 52 = 3 ∙ 25 = 75 Ответ: 75. 22. Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 7 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 5 км/ч? Решение. Туристы затратили на дорогу туда и обратно 4 часа. Пусть х – расстояние, которое проплыли туристы в одну сторону, составим и решим уравнение 𝑥 8 + 𝑥 2 = 4; х + 4 х = 32; 5х = 32; х = 6,4 Ответ: 6,4 км 23. Постройте график функции y = (𝑥−5)(𝑥 2 −6𝑥+8) и определите, при каких значениях m 𝑥−2 прямая y = m имеет с графиком ровно одну общую точку. Решение. Преобразуем выражение функции, разложим квадратный трёхчлен в числителе на множители х2 – 6х + 8 = (х – 2)(х – 4) y= (𝑥−5)(𝑥−2)(𝑥−4) ; y = (x - 5)(x – 4). 𝑥−2 Получили квадратичную функцию, построим ее график Y 0 4 -1 5 X 4,5; - 0,25 прямая y = m будет иметь одну общую точку с графиком функции при трех значениях m. Первый случай, когда прямая касается вершины параболы, т.е. при m = -0,25. Второй случай, когда прямая пересекает параболу в точке x = 4. Подставляя это х в параболу получаем y = m = 0. Третий случай, когда прямая пересекает параболу в точке x = 5. Подставляя это х в параболу получаем y = m = 0. Ответ: -0,25; 0 24. В прямоугольном треугольнике ABC с прямым углом С известны катеты: АС = 15, ВС = 20. Найдите медиану СМ этого треугольника. Решение. В М С А Медиана из прямого угла на гипотенузу равна половине гипотенузы (радиусу описанной окружности около данного треугольника). Гипотенуза равна корню квадратному из 15*15 + 20*20 = 625 или 25 см. Отсюда медиана 1/2 *25 = 12,5 Ответ: 12,5. 25. В параллелограмме KLMN точка B – середина стороны LM. Известно, что BK = ВN. Докажите, что данный параллелограмм – четырехугольник. Решение. L M B K N Проведем дополнительное построение, диагонали AM и LN. Треугольники KBN и LBM равны (MB и BN, LB и KB (по условию), LM и KN (свойство)), значит соответствующие углы равны, т.е. NBK = MBL. Треугольник LBN = MBK(MB и BN, KB и LB (условие), угол LBK общий, NBK = MBL, значит LN = KM, которые являются диагоналями параллелограмма, значит KLMN прямоугольник. 26. Основание АС равнобедренного треугольника АВС равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности, вписанной в треугольник АВС. Решение. 1-й способ. Соединим центры окружностей - вписанной в треугольник АВС и вневписанной. Точку С также соединим с этими центрами. Угол КСО прямой, т.к. равен сумме половин смежных углов ( центры окружностей лежат на биссектрисах углов). Треугольник КСО - прямоугольный. СН в нем -высота и равна половине АС, т.е. равна 5 см. Отрезок ОН равен радиусу вневписанной окружности и равен 9 см. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Из этого следует равенство: СН² = ОН·КН; 25 = 9КН r =КН=25/9 = 2 7 9 2-й способ. Четырехугольники AHO1K и MAKO подобны, так как если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы (т. е. углы, лежащие между пропорциональными сторонами) этих многоугольников равны, то такие многоугольники подобны. 7 5 : r = 9 : 5; 9r = 25; r = 25/9 = 2 7 Ответ: 2 9 9