В 10.
реклама

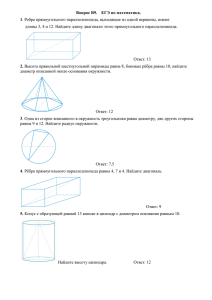
ЕГЭ по математике В 10. Рёбра прямоугольного параллелепипеда равны 4, 7 и 4. Найдите диагональ.(9) В 10. В правильной четырехугольной пирамиде высота равна 12. Площадь основания равна 50. Найдите боковое ребро. (13) В 10. В правильной треугольной пирамиде SABC с вершиной S медиана SL треугольника SAB равна 3. Площадь всей боковой поверхности равна 36. Найдите длину отрезка SB. (5) В 10. Рёбра прямоугольного параллелепипеда равны 2, 9 и 6. Найдите его диагональ. (11) В 10. Сторона ромба равна 15, одна из его диагоналей равна 18. Найдите другую диагональ. (24) В 10. Диагональ прямой призмы равна 13, основание прямоугольник, два ребра его равны 4 и 3. Найдите третье ребро. (12) В 10. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=8, SC=17. Найдите длину отрезка BD. (30) В 10. В прямоугольном параллелепипеде ABCDA1B1C1D1 диагональ AC1=17, ребра AB=9, BC=8. Найти BB1. (12) В 10. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 57√, а высота равна 3. (709) В 10. В прямоугольном параллелепипеде ABCDA1B1C1D1 дано CC1=9, AB=2, BD1=11 . Найдите квадрат длины диагонали BC1. (117) В 10. В правильной треугольной пирамиде SABC точка O — центр основания, S вершина, SO=15, AC=203√. Найдите боковое ребро SA. (25) В 10. SABC --- правильная треугольная пирамида с вершиной S, N — середина ребра BC. Известно, что SN=9, а площадь боковой поверхности равна 81. Найдите длину отрезка AC. (6) В 10. Найдите расстояние между вершинами A и B. (9) ЕГЭ по математике В 13. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 6. (108) В 13. В основании пирамиды лежит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60∘. Найдите объём пирамиды, если высота пирамиды равна 15. (750) В 13. Боковое ребро правильной шестиугольной пирамиды равно 20, сторона основания равна 10. Найдите объём пирамиды. (1500) В 13. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 6. (108) В 13. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). (58) В 13. В основании пирамиды лежит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60∘. Найдите объём пирамиды, если высота пирамиды равна 15. (750) В 13. Боковое ребро правильной шестиугольной пирамиды равно 20, сторона основания равна 10. Найдите объём пирамиды. (1500) В 13. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые). (82)