Зачётная работа № 1, 2010 10 б, в Документ Microsoft Office Word

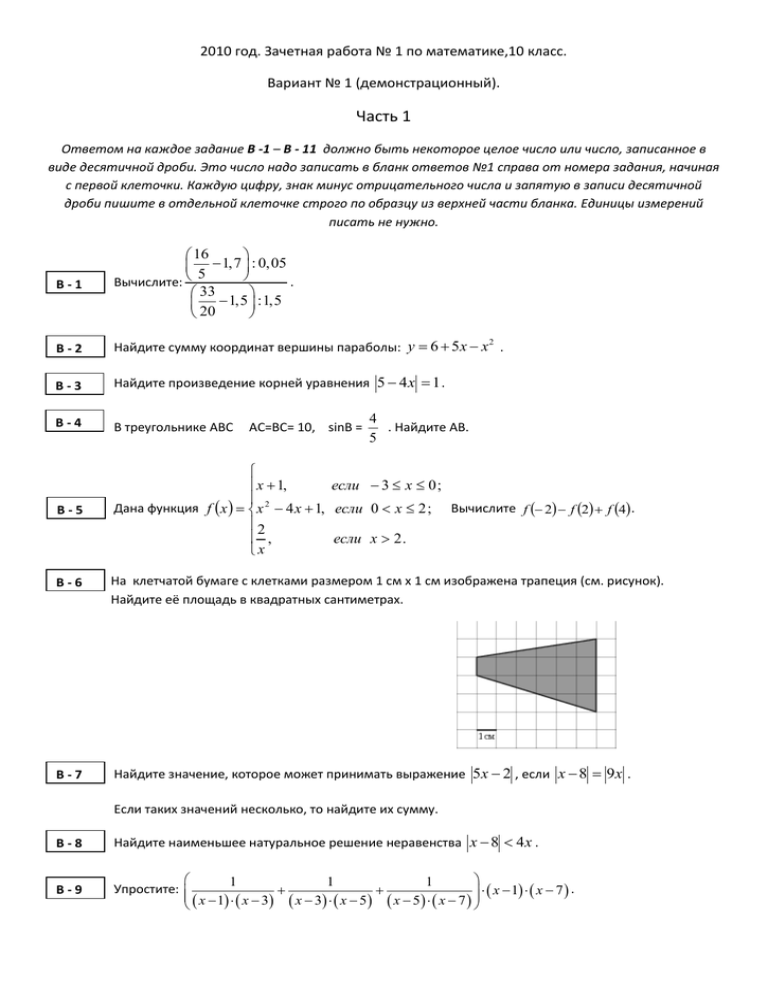
2010 год. Зачетная работа № 1 по математике,10 класс.
Вариант № 1 (демонстрационный).
Часть 1
Ответом на каждое задание В -1 – В - 11 должно быть некоторое целое число или число, записанное в
виде десятичной дроби. Это число надо записать в бланк ответов №1 справа от номера задания, начиная
с первой клеточки. Каждую цифру, знак минус отрицательного числа и запятую в записи десятичной
дроби пишите в отдельной клеточке строго по образцу из верхней части бланка. Единицы измерений
писать не нужно.
В-1
 16

  1,7  : 0,05
5

Вычислите: 
.
 33

  1,5  :1,5
 20

В-2
2
Найдите сумму координат вершины параболы: у  6  5 х  х .
В-3
Найдите произведение корней уравнения 5  4 x  1 .
В-4
В треугольнике АВС
В-5

 x  1,
если  3  х  0 ;
 2
Дана функция f  x    х  4 х  1, если 0  x  2 ; Вычислите f  2  f 2  f 4 .
2
 ,
если x  2 .
x
АС=ВС= 10, sinB =
4
. Найдите АВ.
5
В-6
На клетчатой бумаге с клетками размером 1 см x 1 см изображена трапеция (см. рисунок).
Найдите её площадь в квадратных сантиметрах.
В-7
Найдите значение, которое может принимать выражение 5x  2 , если x  8  9 x .
Если таких значений несколько, то найдите их сумму.
В-8
Найдите наименьшее натуральное решение неравенства x  8  4 x .
В-9
10


1
1
1
Упростите: 
.
  x  1   x  3   x  3   x  5    x  5    x  7     x  1   x  7 


В - 10
10
В - 11
10
Велосипедист каждую минуту проезжает на 2000 м меньше, чем мотоциклист, поэтому на путь в
33 км он затрачивает времени на 2,5 часа больше, чем мотоциклист. Сколько километров в час
проезжает велосипедист?
Найдите радиус окружности, вписанной в прямоугольную трапецию,
если острый угол трапеции равен 600, а большее основание равно 5  5 3 .
Для записи ответов на задания С - 1 – С - 6 используйте бланк
ответов №2. Запишите сначала номер задания (С-1 и т. д.),
а затем полное решение.
1  2x
. Найдите область определения функции y  f x  g x .
3 x
С-1
Пусть f x   2  1  x ; g x  
С-2
Сформулируйте и докажите признак скрещивающихся прямых.
С-3
2
Найдите все целые решения неравенства x  6 x  9  1 , принадлежащие отрезку  2; 7 .
x  3  x  5
Окружность касается одного из катетов равнобедренного прямоугольного треугольника и
С-4
проходит через вершину противолежащего острого угла. Найдите радиус окружности, если её центр лежит на
гипотенузе, длина которой равна
С-5
С-6
1 2
.
4
Найдите все значения параметра
a , при которых уравнение 2 x  3  a 2  2a не имеет решений.
Пусть функция у  f  x  определена на промежутке  2; 0  и убывает на нём.


Решите неравенство f  3 x  2   f 4 x 2  x .