Последняя цифра шифра

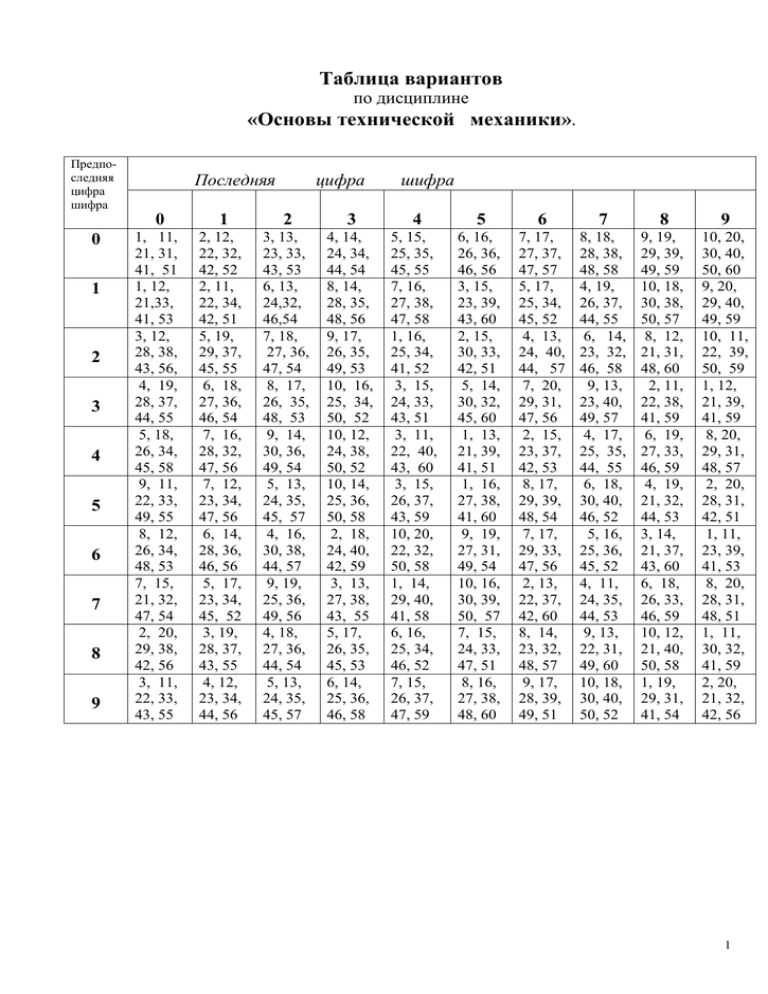
Таблица вариантов
по дисциплине
«Основы технической механики».
Предпоследняя
цифра
шифра
0
1
2
3
4
5
6
7
8
9
Последняя
цифра
шифра
0
1
2
3
4
5
6
7
8
9
1, 11,
21, 31,
41, 51
1, 12,
21,33,
41, 53
3, 12,
28, 38,
43, 56,
4, 19,
28, 37,
44, 55
5, 18,
26, 34,
45, 58
9, 11,
22, 33,
49, 55
8, 12,
26, 34,
48, 53
7, 15,
21, 32,
47, 54
2, 20,
29, 38,
42, 56
3, 11,
22, 33,
43, 55
2, 12,
22, 32,
42, 52
2, 11,
22, 34,
42, 51
5, 19,
29, 37,
45, 55
6, 18,
27, 36,
46, 54
7, 16,
28, 32,
47, 56
7, 12,
23, 34,
47, 56
6, 14,
28, 36,
46, 56
5, 17,
23, 34,
45, 52
3, 19,
28, 37,
43, 55
4, 12,
23, 34,
44, 56
3, 13,
23, 33,
43, 53
6, 13,
24,32,
46,54
7, 18,
27, 36,
47, 54
8, 17,
26, 35,
48, 53
9, 14,
30, 36,
49, 54
5, 13,
24, 35,
45, 57
4, 16,
30, 38,
44, 57
9, 19,
25, 36,
49, 56
4, 18,
27, 36,
44, 54
5, 13,
24, 35,
45, 57
4, 14,
24, 34,
44, 54
8, 14,
28, 35,
48, 56
9, 17,
26, 35,
49, 53
10, 16,
25, 34,
50, 52
10, 12,
24, 38,
50, 52
10, 14,
25, 36,
50, 58
2, 18,
24, 40,
42, 59
3, 13,
27, 38,
43, 55
5, 17,
26, 35,
45, 53
6, 14,
25, 36,
46, 58
5, 15,
25, 35,
45, 55
7, 16,
27, 38,
47, 58
1, 16,
25, 34,
41, 52
3, 15,
24, 33,
43, 51
3, 11,
22, 40,
43, 60
3, 15,
26, 37,
43, 59
10, 20,
22, 32,
50, 58
1, 14,
29, 40,
41, 58
6, 16,
25, 34,
46, 52
7, 15,
26, 37,
47, 59
6, 16,
26, 36,
46, 56
3, 15,
23, 39,
43, 60
2, 15,
30, 33,
42, 51
5, 14,
30, 32,
45, 60
1, 13,
21, 39,
41, 51
1, 16,
27, 38,
41, 60
9, 19,
27, 31,
49, 54
10, 16,
30, 39,
50, 57
7, 15,
24, 33,
47, 51
8, 16,
27, 38,
48, 60
7, 17,
27, 37,
47, 57
5, 17,
25, 34,
45, 52
4, 13,
24, 40,
44, 57
7, 20,
29, 31,
47, 56
2, 15,
23, 37,
42, 53
8, 17,
29, 39,
48, 54
7, 17,
29, 33,
47, 56
2, 13,
22, 37,
42, 60
8, 14,
23, 32,
48, 57
9, 17,
28, 39,
49, 51
8, 18,
28, 38,
48, 58
4, 19,
26, 37,
44, 55
6, 14,
23, 32,
46, 58
9, 13,
23, 40,
49, 57
4, 17,
25, 35,
44, 55
6, 18,
30, 40,
46, 52
5, 16,
25, 36,
45, 52
4, 11,
24, 35,
44, 53
9, 13,
22, 31,
49, 60
10, 18,
30, 40,
50, 52
9, 19,
29, 39,
49, 59
10, 18,
30, 38,
50, 57
8, 12,
21, 31,
48, 60
2, 11,
22, 38,
41, 59
6, 19,
27, 33,
46, 59
4, 19,
21, 32,
44, 53
3, 14,
21, 37,
43, 60
6, 18,
26, 33,
46, 59
10, 12,
21, 40,
50, 58
1, 19,
29, 31,
41, 54
10, 20,
30, 40,
50, 60
9, 20,
29, 40,
49, 59
10, 11,
22, 39,
50, 59
1, 12,
21, 39,
41, 59
8, 20,
29, 31,
48, 57
2, 20,
28, 31,
42, 51
1, 11,
23, 39,
41, 53
8, 20,
28, 31,
48, 51
1, 11,
30, 32,
41, 59
2, 20,
21, 32,
42, 56
1
Общие методические указания
по выполнению домашней контрольной работы
по дисциплине
«Основы технической механики»
Контрольная работа выполняется после изучения всех разделов дисциплины «Основы
технической механики». Задачи контрольной работы даны в последовательности тем программы и поэтому должны решаться по мере изучения материала дисциплины.
Контрольная работа включает 6 задач, которые охватывают наиболее важные разделы
технической механики.
1. Вариант контрольного задания определяется по двум последним цифрам шифра учащегося.
Например, учащийся, имеющий шифр 159, выполняет 59-й вариант. Контрольная работа,
выполненная не по варианту, не зачитывается. Учащийся обязан выполнить контрольную
работу повторно по своему варианту.
2. Контрольная работа должна быть выполнена в обычной школьной тетради (12 листов) в
клетку. На обложке тетради наклеивается стандартный бланк с указанием учебного
заведения, названием дисциплины, с номером контрольной работы и ее вариантом, ФИО
учащегося, его шифра и группы.Домашняя контрольная работа выполняется в обычной
школьной тетради объемом 12 листов ( в клетку). При выполнении контрольной на компьютере должны быть соблюдены следующие требования:
 объем работы - 8-12 страниц формата А4,
 шрифт- 14, Times New Roman,
 межстрочный интервал – одинарный,
 параметры страницы (поля) – 2 см( верхнее), 2см ( нижнее), 3см (левое ) , 1см ( правое) .
3. Текст работы должен быть написан синим стержнем, четким почерком и без помарок. Текст
работы следует писать через строчку. Рисунки и схемы выполняются карандашом четко и
аккуратно.
4. На каждой странице тетради должны быть поля (шириной 2,5-3 см) для заметок
преподавателя.
5. Каждую задачу надо начинать сновой страницы.
6. Необходимо четко указывать номер задачи, тексты условий задач переписываются
обязательно.
7. Должны быть ссылки на теоремы, законы, методы и способы, применяемые для решения
данной задачи. Вычисления рекомендуется выполнять на калькуляторе с точностью до трех
значащих цифр. Вычисления производить в единицах измерения, рекомендуемых
Международной системой (СИ).
8. В конце тетради следует указать литературу, которая была использована при выполнении
контрольной работы.
9. Контрольная работа предоставляется на заочное отделение не позднее срока, указанного в
графике учебного процесса.
10. Проверка и рецензирование домашней контрольной работы осуществляется преподавателем
в течении 7 дней со дня ее поступления на заочное отделение колледжа. По результатам выполнения домашней контрольной работы выставляется «зачтено» или «не зачтено». Отметка «не зачтено» выставляется, если:
 домашняя контрольная работа выполнена не в полном объеме, т.е. освещены не все вопросы
(задачи) варианта учащегося,
 30% и более задач решены не верно,
 имеются грубые ошибки в методике решения задач,
 отдельные задачи контрольной работы не соответствуют варианту учащегося,
 контрольная работа со всей очевидностью выполнена не самостоятельно (несоответствие
почерков, распечатка готовых материалов из Интернета, ксерокопия и т.п.).
2
 работа выполнена небрежно, неразборчивым почерком
11. Незачтенная контрольная работа возвращается учащемуся на доработку. Работу над ошибками следует выполнять в той же тетради, вставив при необходимости дополнительные
листы. В работе над ошибками ответы необходимо исправить точно в соответствии с замечаниями преподавателя, перечисленными в рецензии.
12. Работа, выполненная после установленного учебным графиком срока ее сдачи, принимается на проверку только с разрешения директора колледжа. В период лабораторно - экзаменационной сессии по такой работе может быть проведено устное собеседование (зачет).
13. Учащийся обязан предъявить домашнюю контрольную работу на экзамене по дисциплине
„Основы технической механики.
Рекомендуемая литература
1. Аркуш А.И. Техническая механика. Теоретическая механика и сопротивление материалов. - М., 1989 г.
2. Винокуров Л.И. Сборник задач по сопротивлению материалов. – М., 1990
г.
3. Мовкин М.С., Израелит А.Б. Основы технической механики. – М., 1990 г.
4. Мовкин М.С., Израелит А.Б. Руководство к решению задач по технической механике. – М., 1990 г.
5. Фролов М.И. Техническая механика: Детали машин. – М., 1990 г.
6. Эрдеди А.А., Медведев Ю.А., Эрдеди Н.А. Техническая механика: Теоретическая механика и сопротивление материалов. – М., 1991 г.
7. Рудомор Е.Н., Соколовская В.П. Техническая механика: Сборник заданий.
– М., 1990 г.
Стандарты
ГОСТ 8239 – 89 (СТСЭВ 2209 – 80) Двутавры стальные горячекатанные.
Сортамент.
ГОСТ 8240 – 89 (СТСЭВ 2210 - 80) Швеллеры стальные горячекатанные.
Сортамент.
ГОСТ 8509 – 93 Уголки стальные горячекатанные равноположенные. Сортамент.
3
ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ
по дисциплине
«Основы технической механики»
ЗАДАЧИ 1-10.
Балка закреплена шарнирно в точке А и удерживается в горизонтальном положении стержнем ВС, нагружена силами F1 и F 2 и парой сил с моментом М.
Определить реакции шарнира А и стержня ВС. Схемы нагружения балки показаны на рис. 1.
ЗАДАЧИ 11 – 20.
Определить положение центра тяжести сечения, составленного из прокатных
профилей. Данные для задачи каждого варианта указаны на рис. 2.
ЗАДАЧА 21.
Определить максимальную силу давления автомобиля на арочный мост, если
масса автомобиля 1000кг, скорость его движения V= 72 км/ч.
Радиус кривизны моста r = 500м.
ЗАДАЧА 22.
КПД механической лебедки равен 0,85. Вес поднимаемого груза 1 кг. Груз принимается на высоту 25 м за 20 сек. Какой мощности двигатель установлен на лебедке?
ЗАДАЧА 23.
Груз массой 100 кг опускается равноускоренно с помощью невесомого троса, перекинутого через блок и в первые 4 сек. Проходит 8 м. Определить силу натяжения троса.
ЗАДАЧА 24.
Определить, с каким ускорением должна подниматься вертикально платформа с
телом, если при подъеме тело массой 40 кг давит на платформу с силой 600 н .
ЗАДАЧА 25.
Груз массой 1500 кг, подвешенный на тросе, опускается вертикально вниз с ускорением 3 м/с2 . Найти натяжение троса, пренебрегая его собственной массой.
ЗАДАЧА 26.
Определить, какую силу надо приложить к покоящемуся на гладкой горизонтальной плоскости телу массой 500кг для того, чтобы за время t = 5 сек его скорость
стала равной 20 м/сек. Какой путь пройдет за это время тело?
ЗАДАЧА 27.
Определить, какую постоянную силу надо приложить к телу массой 200 кг,
движущемуся прямолинейно, чтобы на пути 400 м его скорость уменьшилась с 20
м/сек до полной остановки. Найти время движения тела. Силой трения между телом и плоскостью пренебречь.
ЗАДАЧА 28.
Самолет массой 3000 кг для взлета должен иметь скорость 180 км/ч. Время
разгона 30 сек. Найти среднюю величину силы тяги самолета. Силой сопротивления самолета пренебречь.
4
ЗАДАЧА 29.
Определить время разгона тела массой 500кг при действии на него силы 800 н,
если начальная скорость его прямолинейного движения была 36 км/ч, а конечная
скорость- 108 км/ч.
ЗАДАЧА 30.
Тело брошено вертикально вверх с начальной скоростью 49 м/сек. Определить
наибольшую достигнутую им высоту и время подъема тела. Сопротивлением воздуха пренебречь.
ЗАДАЧИ 31 - 40.
Для ступенчатого стального бруса требуется:
А). определить значение продольной силы и нормального напряжения по длине
бруса.
Б). построить эпюры.
В). определить удлинение (укорочение) бруса. Модуль продольной упругости
Е = 2 ∙ 10 МПа.
Данные для каждого варианта указаны на рис. 3.
ЗАДАЧИ 41-50.
Для заданной консольной балки (рис. 4) построить эпюру изгибающих моментов
и подобрать из условия прочности размеры поперечного сечения в двух вариантах:
А). двутавр или сдвоенный швеллер,
Б). прямоугольник с отношением высоты и ширины h/в =3
Сравнить массы балок по обоим расчетным вариантам.
Материал балки- сталь. Ст.3, [ σ ] =160 Мпа.
ЗАДАЧИ 51-60.
Для заданного привода машины (рис.5) необходимо:
А) дать характеристику привода и его отдельных передач,
Б). определить общие КПД и передаточное отношение,
В). определить мощность, вращающие моменты и угловые скорости для всех валов.
При расчетах принять следующие средние значения КПД (с учетом потерь на
трение в опорах валов) передач:
 зубчатая цилиндрическая – 0,97 (закрытая) ; 0,96 (открытая).
 зубчатая коническая – 0,96 (закрытая) ; 0,95 (открытая).
 червячная – 0,8 (закрытая)
 цепная – 0,92 (открытая)
 клиноременная – 0,95 (открытая)
5
1.
2.
3.
4.
5.
Рекомендуемая литература.
Мовнин М.М., Израелит А.Б., Рубашкин А.Г. Основы технической механики.Л.,1982.
Мовнин М.М., Израелит А.Б., Рубашкин А.Г. Руководство к решению задач по
технической механике.-М., 1977.
Аркуша А.И., Фролов М.И. Техническая механика.-М, 1983.
Чернилевский Д.В., Лавров Е.В., Романов В.А. техническая механика.-М., 1982.
Олофинская В.П. Техническая механика.-М.: ФОРУМ-ИНФРА-М,2005
6
Экзаменационные вопросы по дисциплине
«Основы технической механики»
1. Связи и их реакции.
2. Уравнения равновесия плоской системы сходящихся сил.
3. Проекция силы на ось.
4. Пара сил и ее свойства.
5. Уравнение равновесия плоской системы произвольно расположенных сил.
6. Положение центра тяжести простейших сечений.
7. Опорные устройства балочных систем.
8. Скорость точки при равномерном и равноускоренном движении.
9. Ускорение точки.
10.Скорость точки при вращательном движении.
11.Угловая скорость и угловое ускорение.
12.Работа постоянной силы при прямолинейном перемещении.
13.Работа и мощность при вращательном движении.
14.Коэффициент полезного действия.
15.Понятие силы инерции.
16.Построение эпюр продольных сил.
17.Определение удлинения при растяжении и сжатии.
18.Закон Гука при растяжении и сжатии.
19.Расчеты на прочность при срезе и смятии.
20.Расчеты на прочность при растяжении и сжатии.
21.Расчеты на прочность при кручении.
22.Расчеты на прочность при изгибе.
23.Продольная и поперечная деформации при растяжении и сжатии.
24.Передаточное число.
25.Классификация механических передач.
26.Зубчатые передачи.
27.Червячные передачи.
28.Цепные и ременные передачи.
29.Резьбовые соединения.
30.Шпоночные соединения.
31.Шлицевые соединения.
32.Кулачковые механизмы.
33.Храповые механизмы.
34.Мальтийские механизмы.
35.Кривошипно-шатунный механизм.
36.Подшипники скольжения.
37.Подшипники качения.
38.Муфты.
39.Определение вращающих моментов на валах привода.
40.Определение передаточных чисел простейших передач.
41.Определение передаточных чисел многоступенчатых передач.
42.Зависимость вращающего момента от угловой скорости.
7
Методические указания
по решению задач № 1 – 10
Задачу №1 следует решать после изучения тем: «Основные понятия и аксиомы
статики»; «Плоская система произвольно расположенных сил»; «Пара сил». Во
всех задачах следует определить реакции шарнира и стержня.
Последовательность решения задачи:
1. Изобразить балку вместе с нагрузками.
2. Выбрать расположение координатных осей, совместить ось х с осью балки, а
ось у направив перпендикулярно оси х.
3. Произвести необходимые преобразования: силу, наклоненную к оси балки под
углом, заменить двумя взаимно перпендикулярными составляющими, реакцию
стержня, наклоненную под углом к оси балки, также заменить двумя взаимно
перпендикулярными составляющими.
4. Освободить балку от связей (опоры и стержня), заменив их действие реакциями.
5. Составить уравнения равновесия статики для произвольной плоской системы
сил таким образом и в такой последовательности, чтобы решением каждого из
этих уравнения было определение одной из неизвестных реакций.
6. Проверить правильность найденных реакций по уравнению, которое не было
использовано для решения задачи.
Пример 1. Балка закреплена шарнирно в точке А и удерживается в горизонтальном положении стержнем ВС, нагружена силами F1 и F2 и парой сил с моментом
М. Определить реакции ширнира А и стержня ВС.
M = 10 кHм
C
F2 = 20 кH
o
60
A
F1 = 10 кH
4м
2м
M
Y
B
2м
C
F2 x
A
F1
YA
XA
A
M
F1
B
X
F2 y
Rc
B
F2 x
F2 y
8
Решение.
1. Изобразим балку с действующими на неё нагрузками.
2. Изображаем оси координат х и у.
3. Силу F заменяем её составляющими Fx и Fy; Fx = F cosλ и Fy = F sinλ.
F2x = F2 cos 60 = 20 ½ = 10 кН
F2y = F2nn sin 60 = 20 3/2 = 17 кН
4. Освобождаем балку от связей, заменив их реакциями.
5. Составляем уравнения равновесия статики и определяем неизвестные реакции
связей.
ΣFkx = 0; - xA + F2x = 0; xA = F2x = 10 кН
ΣMA (F) = 0; -F1 ·2 + M + Rc · 6 + F2y · 8 = 0
Rc · 6 = -F1 ·2 + M +F2y · 8; 6Rc = - 20 + 10 + 136; Rc = 21 кН
ΣMB (F) = 0; yA · 6 + F1 · 4 + M + F2y · 2 = 0
6yA = - F1 · 4 – M – F2y · 2; 6yA = - 40 – 10 – 34 = - 84; yA = - 14 кН
6.
Проверяем правильность найденных результатов:
Σfky = yA + F1 + Rc – F2y = - 14 + 10 + 21 – 17 = - 31 + 31 = 0
Условие равновесия ΣFky = 0 следовательно, реакции найдены верно.
Ответ: хА = 10 кН; уА = - 14 кН; Rс = 21 кН.
Пример 2. Балка закреплена шарнирно в точке А и удерживается в
горизонтальном положении стержнем ВС, нагружена силами F1 и F2 и парой сил с
моментом М.
Определить реакции шарнира А стержня ВС.
F1 = 10 кH
F2 = 20 кH M=16кHм
A
60o
B
Rc
C
4м
4м
2м
Y
F1
B
X
Rc
C
Ryc
Rxc
M
F2
YA
F1
C
F2
A
M
XA
9
Решение.
1. Изобразим балку с действующими на ней нагрузками.
2. Изображаем оси координат х и у.
3.
Реакцию Rc заменим ее составляющими Rcx и Rcy.
4.
Освобождаем балку от связей, заменив их реакциями.
Rcx = Rc cos 60
Rcy = Rc sin 60
5.
Составляем уравнения статики и определяем неизвестные реакции связей.
ΣMB (F) = 0; F1 · 4 + F2 · 8 – M – yA ·10 = 0
10yA = F1 · 4 + F2 · 8 – M; 10yA = 40 + 160 – 16 = 184; yA = 18,4 кН
ΣMA (F) = 0; Rcy ·10 – F1 · 6 – F2 · 2 – M = 0
10Rcy = F1 · 6 + F2 · 2 + M; 10Rcy = 60 + 40 + 16 = 116; Rcy = 11,6 кН
Rc = Rcy / sin 60 = 11,6 / √3/2 = 23,2 / 1,7 = 13,65 кН
Rcx = 13,65 · ½ = 6,82 кН
ΣFkx = 0; - Rcx + xA = 0; xA = Rcx = 6,82 кН
6.
Проверяем правильность найденных результатов.
ΣFky = yA – F1 – F2 + Rcy = 18,4 – 10 – 20 + 11,6 = 30 – 30 = 0
Условие равновесия ΣFky = 0 реакции найдены верно.
Ответ: хА = 6,82 кН; уА = 18,4 кН; Rс = 13,65 кН.
10
Методические указания
по решению задач № 11 - 20
Определить положение центра тяжести сечения, составленного из прокатных
профилей.
Последовательность решения задач:
1.
Выбрать метод, который наиболее применим к данной задаче (метод
группировок или метод отрицательных масс).
2.
Разбить сложное тело на простые элементы, для которых центра тяжести
известны.
3.
Выбрать оси координат. При этом необходимо помнить, что если тело
имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если
тело имеет центр симметрии, то его центр тяжести совпадает с центром
симметрии.
4.
Определить координаты центров тяжести отдельных простых тел
относительно только выбранной оси.
5.
Определить искомые координаты центра тяжести по формам:
xc = ΣAk · xk / ΣAk; yc = ΣAk · yk / ΣAk, где
Ак - площадь элементарной площадки;
хк; ук – координаты центра тяжести элементарной площадки;
хс; ус – координаты центра тяжести плоского сечения.
Пример 1. Определить положение центра тяжести сечения, составленного из
сечений двутавра № 22 и швеллера № 20.
Так как сечение, составленное из сечений двутавра и швеллера, представляет
собой фигуру, симметричную относительно оси у, то центр тяжести плоского
сечения лежит на той оси, т.е хс = 0.
Y
Z0
d
2№20
C2
h1
C
Y1
YC
Y2
C1
1№22
X
Решение.
1.
По справочнику определяем площади и координаты центров тяжести
двутавра и швеллера:
- Двутавр № 22 (ГОСТ 8239.72) высота h1 = 220 мм, ширина полки b = 110 мм, А1
= 30,6 см2.
11
- Швеллер № 20 (ГОСТ 8240 – 72) высота h = 200 мм, ширина полки b = 80 мм, zo
= 2,07 см, d = 5,2 мм, А2 = 23,4 см2.
2.
Кординаты центров тяжести каждой фигуры можно определить по
чертежа.
y 1 = h1 / 2 = 220 / 2 = 110 мм = 11 см
у2 = h1 + d – zo = 220 + 5,2 – 20,7 = 204,5 мм= 20,4 см
3.
Определяем координаты центра тяжести всего сечения.
xc = 0; yc = A1 ·y1 + A2 · y2 / A1 + A2 = 30,6 · 11 + 23,4 · 20,4 / 30,6 + 23,4 = 15,07 см
Ответ: хс = 0; ус = 15,07 см
Пример 2. Определить координаты центра тяжести составного сечения. Сечение
состоит из листа и прокатных профилей.
Примечание: часто рамы сваривают из разных профилией, создавая необходимую
конструкцию.
Таким образом, уменьшается расход металла и образуется конструкция высокой
прочности.
Y
1№10
30
C1
h2
Y1
C
2№16
C3
Y3
5
YC
Y2
C2
X
100
Решение.
1. Обозначим фигуры номерами и выпишем из таблиц необходимые данные:
 Швеллер № 10 (ГОСТ 8240 – 72): h = 100 мм, ширина полки b = 40 мм, А1 =
10,9 см2, zo = 1,44 см.
 Двутавр № 16 (ГОСТ 8239 – 72): высота h = 160 мм, ширина полки 81 мм, А2 =
20,2 см2.
 Лист 5×100; площадь А3 = 0,5 · 10 = 5 см2.
12
2.
Координаты центров тяжести каждой фигуры можно определить по
чертежу. Составное сечение симметрично, поэтому центр тяжести находится на
оси симметрии и координата хс = 0.
Швеллер у1 = h2 + zo + a = 16 + 1,44 + 0,5 = 17,54 см.
Двутавр у2 = а + h2 / 2 = 0,5 + 16/2 = 8,5 см.
Лист 3 у3 = а / 2 = 0,5 / 2 = 0,25 см.
3.
Определение центра тяжести составленого сечения.
xc = 0;
yc = A1 · y1 + A2 · y2 + A3 · y3 / A1 · A2 ·A3 = 10,9 · 17,54 + 20,2 · 8,5 + 5 · 0,25 /
/ 10,9 + 20,2 + 5 = 10 см.
Ответ: хс = 0; ус = 10 см.
13
Методические указания
по решению задач № 21 - 30
Теоретические сведения, необходимые для решения задач № 21 – 30.
Динамика – раздел теоретической, в котором устанавливается связь между
движением тел и действующими на них силами.
В динамике решают два типа задач:
- определяют параметры движения по заданным силам;
- определяют силы, действующие на тело, по заданным кинематическим
параметрам движения.
Аксиомы динамики.
Первая аксиома (принцип инерции). Всякая изолированная материальная точка
находится в состоянии покоя или равномерного и прямолинейного движения,
пока приложенные силы не выведут её из того состояния.
Вторая аксиома (основной закон динамики): F = m · a.
Третья аксиома. Сила взаимодействия двух тел равна по величине и направлена
по одной прямой в разные стороны.
Четвертая аксиома (закон независимости действия сил).
Сила инерции
Сила инерции – сила, возникающая при разгоне или торможения тела и
направленная в обратную сторону от ускорения. Силу инерции можно измерить,
она приложена к связям – телам, связанным с разгоняющимся или тормозящимся
телом.
Fин1
Fин2
m1
m2
Fдв
а
Сила инерции равна Fин = (ma).
Такми образом, силы, действующие на материальные точки m1 и m2, при разгоне
платформы соответственно равны Fин1 = m1 · а; Fин2 = m2 · а.
14
При вращательном движении (криволинейном) возникающее ускорении принято
представлять в виде двух составляющих: нормального aп и касательного аτ.
Поэтому при рассмотрении криволинейного движения могут возникнуть две составляющие силы инерции: нормальная и касательная а = аτ + ап.
аτ = d ·v / d · t = v; аτ = ε · z; Fτ ин = m · ε · z;
an = v2 / 2; Fинn = m · v2 / 2
Принцип кинетостатики (принцип Даламбера).
Принцип кинетостатики используют для упрощения решения ряда технических
задач. Даламбер предложил условно прикладывать силу инерции к активно
разгоняющемуся телу. Тогда система сил, приложенных к материальной точке,
становиться уравновешенной и можно при решении задач динамики использовать
уравнения статики.
Принцип Даламбера.
Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии:
ΣFk + ΣRk + Fин = 0; Fин = - mа.
1.
2.
3.
4.
5.
6.
Последовательность решения задач
с использованием принципа Даламбера:
Составить расчетную схему.
Выбрать систему координат.
Выяснить направление и величину ускорения.
Условно приложить силу инерции.
Составить систему уравнений равновесия.
Определить неизвестные величины.
r
v
15
Пример 1. Мотоциклист въезжает на деревянный мост и прогибает его. Радиус
кривизны моста 100 м. Сила тяжести мотоцикла с мотоциклистом 1500 Н. Скорость мотоцикла 12 км/ч. Определить силу прижатия мотоцикла к поверхности
моста.
Дано. r = 100 м, G = 1500 Н, v = 72 км/ч.
Определить N.
Решение.
1.
Составляем расчетную схему.
2.
Проводим оси координат.
3.
Так как мотоцикл перемещается по криволинейной траектории, то возникает нормальное ускорение, направленное по нормали к траектории движения, к
центру её кривизны.
Тогда сила инерции будет равна Fинп = m · an, направлена сила инерции противоположно нормальному ускорению.
4.
Составляем уравнение равновесия:
ΣFky = 0; N – G - Fun = 0, где
N – реакция моста, или та же сила, что и сила прижатия мотоцикла к поверхности
моста. Так как сила с положение взаимодействуют тела равны между собой и
противоположны по направлению.
5.
Решаем уравнение.
N = G + Fun;
G = m · g;
Fun = m · an
an = v2 / z;
v = 72 км/час = 20 м/с
N = m · g + m · v2 / z = m (g + v2 / z) = 1500 (9,8 + 400 / 100)
N = 20700 Н
Ответ. N = 20700 Н.
16
Методические указания
по решению задач № 31 - 40
Для ступенчатого стального бруса требуется:
а) Определить значение продольной силы и нормального напряжения по
длине бруса.
б) Построить эпюры.
в) Определить удлинение (укорочение) бруса. Модуль продольной упругости
Е = 2 · 10 5 Мпа.
Последовательность выполнения задачи:
1. Разбить брус на участки. Границами участков являются точки приложения
сил и листа изменения размеров поперечного сечения.
2. Определить по методу сечений продольную силу для каждого участка, построить эпюру продольных сил.
3. Определить нормальные напряжения на каждом участке и построить эпюру нормальных напряжений.
4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисляемых по формуле Гука.
Пример 1. Для данного ступенчатого бруса построить эпюру продольных
сил, определить перемещение свободного конца, если Е = 2 · 105 МПа.
F1 = 30 кН;
F2 = 38 кН;
F3 = 42 кН;
A1 = 1,9 см2;
А3 = 3,1 см2.
17
Решение.
1. Разбиваем брус на участки.
2. Методом сечений определяем продольную силу на каждом участке.
N1 = 0; N2 = F1 = 30 кН; N3 = F1 = 30 кН; N4 = F1 – F2 = - 8 кН;
N5 = F1 – F2 – F3 = - 50 кН.
3. Строим эпюру продольных сил. Вычисляем значения нормальных напряжений.
σ1 = N1 / A1 = 0; σ2 = N2 / A1 = 30 · 103 / 1,9 ·102 = 158 Н/мм2 = 158 МПа
σ3 = N3 / A2 = 30 · 103 / 3,1 · 102 = 96,8 Н/мм2 = 96,8 МПа
σ4 = N4 / A2 = - 8 · 103 / 3,1 · 102 = - 25,8 Н/мм2 = - 25,8 МПа
σ5 = N5 / A2 = - 50 · 103 / 3,1 · 102 = - 163 Н/мм2 = - 163 МПа
4. Определяем перемещение свободного конца.
Δl = Δl 1 + Δl 2 + Δl 3 + Δl 4 + Δl 5.
Δl 1 = N1 · l 1 / E · A1 = 0;
Δl 2 = N2 · l 2 / E · A1 = 30 · 103 · 0,5 · 103 / 2 · 105 · 1,9 · 102 = 0,394 мм
Δl 3 = N3 · l 3 / E · A2 = 30 · 103 · 0,1 · 103 / 2 · 105 · 3,1 · 102 = 0,0484 мм
Δl 4 = N4 · l 4 / E · A2 = - 8 · 103 · 0,4 · 103 / 2 · 105 · 3,1 · 102 = - 0,0516 мм
Δl 4 = N4 · l 4 / E · A2 = - 50 · 103 · 0,2 · 103 / 2 · 105 · 3,1 · 102 = - 0,161 мм
Δl = 0,394 + 0,0484 – 0,161 = 0,23 мм
18
Методические указания
по решению задачи № 41 - 50
Для заданной консольной балки построить эпюру из изгибающих моментов и
подобрать из условия прочности размера поперечного сечения в двух вариантах:
а) двутавр или сдвленный швеллер;
б) прямоугольник с отношением высоты и ширины h / b = 3. Сравнить массы балок по обоим расчетным вариантам.
Материал балки – сталь Ст3, [σ] = 160 МПа.
Пример 1.
Решение.
1. Строим эпюру изгибающих моментов по характерным точкам.
МА = 0; МВ = F2 · 4 = 20 · 4 = 80 кНм
Мс = - F1 · 2 + F2 · 6
Мспр = - 45 · 2 + 20 · 6 = - 90 + 120 = 30 кНм
Мслев = - М – F1 · 2 + F2 · 6 = - 25 – 90 + 120 = - 5 кНм
МДпр = F2 · 8 – F1 · 4 – М = 20 · 8 – 45 · 4 – 25 = - 45 кНм
2. Определяем опасное сечение. Опасное сечение балки, где действует максимальный момент. Это сечение В, в нем Мин = 80 кНм.
3. Подбираем размеры балки в опасном сечении по условию прочности.
σиmax = Миmax / Wх ≤ [σ];
Wх ≥ Ми max / [σх]
3
3
Wх = 80 · 10 · 10 / 160 = 500 · 103 мм3 = 500 см3.
По таблице ГОСТ 8239 – 89 выбираем двутавр № 30а: момент сопротивления
Wх = 518 см3; А = 49,9 см2, А – площадь сечения.
19
Для сравнения рассчитаем размер балки квадратного сечения при том же моменте сопротивления сечения.
Wx = b3 / 6; Wx = 500 см3 = b3 / 6; b ≥ √6Wx.
b = 3 √6 · 500 = 14.5 см,
b – сторона квадрата.
2
2
2
А = b = 14,5 = 200,2 см .
А – площадь сечения квадрата.
Аквадрата / Адвутавра = 200,2 / 49,9 = 4,2
Балка квадратного сечения в 4 раза тяжелее.
Пример 2.
F1 = 15 кН; F2 = 18 кН;
F3 = 5 кН; М = 20 кНм
Решение.
1.
Строим эпюру изгибающих моментов по характерным точкам.
МВ = 0;
Мслев = - F1 ·2 = - 30 кНм
Мспр = - F1 · 2 + М = - 30 + 20 = - 10 кНм
МДлев = - F1 · 5 + М = - 75 + 20 = - 55 кНм
МЕлев = - F1 · 7 + М – F2 · 2
МЕлев = - 15 · 7 + 20 – 18 · 2 = - 121 кНм
МАлев = - F1 · 9 + М – F2 · 4 + F3 · 2
МВлев = - 15 · 9 + 20 – 18 · 4 + 5 · 2 = - 177 кНм
2.
Определяем опасные сечения. Опасные сечения балки, где изгибающей
момент наибольший. Это сечение А, в нем МА = 177 кНм.
3.
Подбираем размеры балки в опасном сечении по условию прочности.
σиmax = Mumax / Wx ≤ [σ];
Wx = Mumax / [σ] = 177 · 103 · 103 / 160 = 1106 ·103 мм3 = 1106 см3
Так как сечение балки сдвоенный швеллер, то Wx = 1106 / 2 = 553 см3.
По таблице ГОСТ 8240 – 89 выбираем швеллер № 36; момент сопротивления Wx =
601 см3;
А = 53,4 см2. А - площадь сечения.
Для сравнения рассчитываем размеры балки прямоугольного сечения при том же
моменте сопротивления.
Wx = b · h2 / 6;
h/b=3
2
Wx = b · 9 · b / 6 = 3 / 2 · b3
Wx = 553 см3 = 3 / 2 · b3;
b = 3√2 · Wx / 3; b = 3 √2 · 553 / 3 = 7,17 см
h = 3 · b = 21,51 см
А = b · h = 7,17 · 21,51 = 154,155 см2
Апр / Алев = 154,155 / 53,4 · 2 = 1,4.
Балки прямоугольного сечения в 1,4 раза тяжелее
20
21
Методические рекомендации
по решению задач № 51 - 60
Краткие теоретические сведения,
необходимые для решения задач № 51 – 60.
Передачами называются механизмы, служащие для передачи механической
энергии на расстоянии.
Наиболее распространены механические передачи вращательного движения.
Это связано с таким преимуществом вращательного движения, как возможность
обеспечения его непрерывности и равномерности при малых потерях трения.
Кроме того, вращательное движение позволяет получить простую и надежную
конструкцию передачи малых габаритов.
По принципу передачи движения от ведущего звена к ведомому передачи делятся на две группы: передачи с трением - с непосредственным контактом жестких тел (фрикционные) и гибкой связью (ременные); передачи зацеплением – с
непосредственным контактом твердых тел (зубчатые, винтовые и червячные) и
гибкой связью (цепные, зубчатым ремнем).
Кинематические и силовые соотношения в передачах.
В каждой передаче различают два основных вала: ведущий и ведомый.
Ведущий вал получает движение от двигателя. Ведомый вал получает движение
от ведущего.
Силовые характеристики передачи: мощность Р1 на ведущем и Р2 ведомом валах, кВт; угловая скорость ω1 ведущего и ω2 ведомого валов, рад/с или частоты
вращения п1 ведущего и п2 ведомого валов, об/мин.
Кроме силовых различают производные характеристики: коэффициент полезного
действия (КПД) передачи: η = Р2 / Р1.; вращающий момент, М = Р/ω.Нм.
М1 = Р1 / ω1 – это момент движущихся сил и его направление совпадает с направлением вращения вала; момент на ведомом валу М2 = Р2 / ω2 – это момент сил сопротивления, его направление противоположно направлению вращения вала.
При расчете передач чисто пользуется зависимостью между вращающими
моментами на валах. Эту зависимость получим, разделив вращение момента М2 и
М1.
М2 / ω1 = Р2 · ω1 / Р1 · ω2 = η · п,
где п – передаточное число.
п = ω1 / ω2 = d2 / d1 или п = п1 / п2
Для зубчатой передачи передаточное число п = z2 / z1,
где z2 – число зубьев зубчатого колеса;
z1 – число зубьев шестерни.
Если одной парой зубчатых колес нельзя обеспечить требуемое передаточное
число, то применяют ряд последовательно соединенных одноступенчатых передач, так называемую многоступенчатую передачу. Ее общее передаточное число
Uобщ = U1 · U2 · … · Un, где
U1, U2, … Un – передаточное число каждой ступени.
Общий КПД многоступенчатой передачи
ηобщ = η1 · η2 · … · ηп, где
22
η1 , η2 ,… ηп – КПД каждой кинематической, пары (зубчатой, червячной, ременной
и др), а также других звеньев привода, где имеются потери мощности (подшипники, муфты и т.д.).
Пример 1. Выполнить кинематический и силовой двухступенчатый привода,
включающие электродвигатель 1, ременную передачу 2, редуктор цилиндрический одноступенчатый 3.
Рэл = 7,17 кВт;
ωдв = 152,3 рад/с
D1 = 100 мм;
D2 = 200 мм
z1 = 18
z2 = 54
2
3
1
U
Решение.
1. Определяем общее передаточное число.
Uобщ = U1 · U2;
U1 = D2 / D1 = 200 / 100 = 2; U2 = z2 / z1 = 54 / 18 = 3
Uобщ = 2 · 3 = 6
2. Определяем общий коэффициент полезного действия
ηобщ = η1 · η2, где
η1 – КПД ременной передачи;
η2 – КПД закрытой прямозубой передачи;
ηобщ = 095 · 0,97 = 0,9215
3. Определяем угловую скорость каждого вала.
ω1 = ωдв = 152,3 рад/с
ω1 / ω2 = U1 = 2;
ω2 = ω1 / 2 = 152,3 / 2 = 76,15 рад/с
ω3 = ω2 / 3 = 25,38 рад/с
4. Определяем мощность каждого вала
Р2 = Рдв · η1 = 7,17 · 0,95 = 6,81 кВт
Р3 = Рдв · ηобщ = 7,17 · 0,9215 = 6,6 кВт
5. Определяем вращающий момент на каждом валу.
М = Р / ω; М2 = Р2 / ω2 = 6,81 · 103 / 76,15 = 89,43 Нм
Мдв = Рдв / ωдв = 7,17 · 103 / 152,3 = 47 Нм
М3 = Р3 / ω3 = 6,6 · 103 / 25,38 = 260 Нм
23
Сталь горячекатаная. ШВЕЛЛЕРЫ (по ГОСТ 8240 – 89)
Обозначения:
h – высота швеллера; b – ширина швеллера; d – толщина стенки; t – средняя толщина полки; А – площадь швеллера; J – момент инерции; W – момент сопротивления; i – радиус инерции; S – статический момент полусечения; zo – расстояние от
оси у до наружной грани стенки.
Таблица 1
№
профиля
5
6,5
8
10
12
14
16
18
20
22
24
27
30
33
36
40
Размеры, мм
h
b
d
t
А,
см2
50
65
80
100
120
140
160
180
200
220
240
270
300
330
360
400
32
36
40
46
52
58
64
70
80
82
90
95
100
105
110
115
4,4
4,4
4,5
4,5
4,8
4,9
5
6,1
5,2
5,4
5,6
6,0
6,5
7,0
7,5
8,0
7,0
7,2
7,4
7,6
7,8
8,1
8,4
8,7
9,0
9,5
10,0
10,5
11,0
11,7
12,6
13,5
6,16
7,51
8,98
10,9
13,3
15,6
18,1
20,7
23,4
26,7
30,6
35,2
40,5
46,5
53,4
61,5
Jx ,
см4
Wx,
см3
iх,
см
Sx,
см3
Jy,
см4
Wу,
см3
iу,
см
Zо,
см3
22,8
48,6
89,4
174
304
491
747
1090
1520
2110
2900
4160
5810
7980
10820
15220
9,1
15,0
22,4
34,8
50,6
70,2
93,4
121
152
192
242
308
387
484
601
761
1,92
2,54
3,16
3,99
4,78
5,60
6,42
7,24
8,07
8,89
9,73
10,9
12,0
13,1
14,2
15,7
5,59
9,00
13,3
20,4
29,6
40,8
54,1
69,8
87,8
110
139
178
224
281
350
444
5,61
8,70
12,8
20,4
31,2
45,4
63,6
86
113
151
208
262
327
410
513
642
2,75
3,68
4,75
6,46
8,52
11,0
13,8
17
20,5
25,1
31,6
37,3
43,6
51,8
61,7
73,4
0,954
1,08
1,19
1,37
1,53
1,70
1,87
2,04
2,20
2,37
2,60
2,73
2,84
2,97
3,10
3,23
1,16
1,24
1,31
1,44
1,54
1,68
1,80
1,94
2,07
2,21
2,42
2,47
2,52
2,59
2,68
2,75
24
Сталь горячекатаная.
БАЛКИ ДВУТАВРОВЫЕ (по ГОСТ 8239 – 89)
Обозначения:
h – высота балки; b – ширина балки; d – толщина стенки; t – средняя толщина полки;
А – площадь сечения; J – момент инерции; W – момент сопротивления; i – радиус
инерции; S – статический момент полусечения.
Таблица 2
№
Размеры, мм
А,
Jx ,
Wx,
iх,
Sx,
Jy,
Wу,
iу,
про2
4
3
3
4
3
см
см
см
см
см
см
см
см
h
b
d
t
филя
10 100 55
4,5
7,2 12,0 198 39,7 4,06 23,0 17,9 6,49 1,22
12 120 64
4,8
7,3 14,7 350 58,4 4,88 33,7 27,9 8,72 1,38
14 140 73
4,9
7,5 17,4 572 81,7 5,73 46,8 41,9 11,5 1,55
16 160 81
5,0
7,8 20,2 873 109 6,57 62,3 58,6 14,5 1,70
18 180 90
5,1
8,1 23,4 1290 143 7,42 81,4 82,6 18,4 1,88
20 200 100 5,2
8,4 26,8 1840 184 8,28 104 115 23,1 2,07
22 220 110 5,4
8,7 30,6 2550 232 9,13 131 157 28,6 2,27
24 240 115 5,6
9,5 34,8 3460 289 9,97 163 198 34,5 2,37
27 270 125 6,0
9,8 40,2 5010 371 11,2 210 260 41,5 2,54
30 300 135 6,5
10,2 46,5 7080 472 12,3 268 337 49,9 2,69
33 330 140 7,0
11,2 53,8 9840 597 13,5 339 419 59,9 2,79
36 360 145 7,5
12,3 61,9 13380 743 14,7 423 516 71,1 2,89
40 400 155 8,3
13,0 72,6 19062 953 16,2 545 667 86,1 3,03
45 450 160 9,0
14,2 84,7 27696 1231 18,1 708 808 101 3,09
50 500 170
10
15,2 100 39727 1589 19,9 919 1043 123 3,23
55 550 180
11
16,5 118 55962 2035 21,8 1181 1356 151 3,39
60 600 190
12
17,8 138 76806 2560 23,6 1725 1725 182 3,54
25
Сталь прокатная угловая равнополочная
(по ГОСТ 8509 – 86)
Обозначения:
b – ширина полки; d – толщина полки;
J – момент инерции; i – радиус инерции W – момент сопротивления; zо –
расстояние от центра тяжести до
наружной грани полки; А – площадь
уголка.
Таблица 3
Но- Размеры, мм
мер
угол- b
d
ка
2
20
3
4
2,5
25
3
4
2,8
28
3
3,0
30
3
4
3,2
32
3
4
3,5
35
3
4
3,5
35
5
4,0
40
3
4
5
45
45
3
4
5
5,0
50
3
4
5
6
5,6
56
4
5
6,0
60
4
5
6
8
А,
см2
1,13
1,46
1,43
1,86
1,62
1,74
2,27
1,86
2,43
2,04
2,17
3,28
2,35
3,08
3,79
2,65
3,48
4,29
2,96
3,89
4,80
5,69
4,38
5,41
4,72
5,83
6,92
9,40
Jx,
см4
0,40
0,50
0,81
1,03
1,16
1,45
1,84
1,77
2,26
2,35
3,01
3,61
3,55
4,58
5,53
5,13
6,63
8,03
7,11
9,21
11,20
13,07
13,10
15,97
16,21
19,79
23,21
29,55
х–х
Wx,
см4
0,28
0,37
0,46
0,59
0,58
0,67
0,37
0,77
1,00
0,93
1,21
1,47
1,22
1,60
1,95
1,56
2,04
2,51
1,94
2,54
3,13
3,69
3,21
3,96
3,70
4,56
5,40
7,00
Справочные величины для осей
хо - хо
у о - уо
iх, Jxo max, iхo max, Jyo min, Wyo min, iyo min,
см
см4
см
см4 см4
см
0,59 0,63 0,75 0,17 0,20 0,39
0,58 0,78 0,73 0,22 0,24 0,38
0,75 1,29 0,95 0,34 0,33 0,49
0,74 1,62 0,93 0,44 0,41 0,48
0,85 1,84 1,07 0,48 0,42 0,55
0,91 2,30 1,15 0,60 0,53 0,59
0,80 2,92 1,13 0,77 0,61 0,58
0,97 280 1,23 0,74 0,59 0,63
0,96 3,58 1,21 0,94 0,71 0,62
1,07 3,72 1,35 0,97 0,71 0,69
1,06 4,76 1,33 1,25 0,88 0,68
1,05 5,71 1,32 0,52 1,02 0,68
1,23 5,63 1,55 1,47 0,95 0,79
1,22 7,26 1,53 1,90 1,19 0,78
1,21 8,75 1,52 2,30 1,39 0,78
1,39 8,13 1,75 2,12 1,24 0,89
1,38 10,52 1,74 2,74 1,54 0,89
1,37 12,74 1,72 3,33 1,81 0,88
1,55 11,27 1,95 2,95 1,57 1,00
1,54 14,63 1,94 3,80 1,95 0,99
1,53 17,77 1,92 4,63 2,30 0,98
1,52 20,72 1,91 5,43 2,63 0,98
1,73 20,79 2,18 5,41 2,52 1,11
1,72 25,36 2,16 6,59 2,97 1,10
1,85 25,69 2,33 6,72 2,93 1,19
1,84 31,40 2,32 8,18 3,49 1,18
1,83 36,81 2,31 9,60 3,99 1,18
1,81 46,77 2,27 12,34 4,90 1,17
zо ,
см2
0,60
0,64
0,73
0,76
0,80
0,85
0,89
0,89
0,94
0,97
1,01
1,05
1,09
1,13
1,17
1,21
1,26
1,30
1,33
1,38
1,42
1,46
1,52
1,57
1,62
1,66
1,70
1,78
26
Но- Размеры, А,
мер
мм
см2
угол- b
d
ка
6,3
63
7,0
70
7,5
75
7,5
75
8,0
80
9,0 90
10 100
11 110
12,5 125
14
140
15
16
150
160
18
20
180
200
22
25
220
250
10
4
5
6
4,5
5
6
8
8
5
6
7
8
9
5,5
6
7
8
6
10
16
8
12
14
16
10
12
15
10
16
12
12
14
20
30
14
20
25
30
Справочные величины для осей
хо - хо
Jx,
Wx, iх,
4
см
см4 см
11,08 35,32 8,52 1,79
4,69 18,86 4,09 1,95
6,13 23,10 5,05 1,94
7,28 27,06 5,98 1,93
6,20 29,04 5,67 2,16
6,86 31,94 6,27 2,16
8,15 37,58 7,43 2,15
9,42 42,98 8,57 2,14
10,67 48,16 9,68 2,12
7,39 39,53 7,21 2,31
8,78 46,57 8,57 2,30
10,15 53,34 9,89 2,29
11,50 59,84 11,18 2,28
12,83 66,10 12,43 2,27
8,63 52,68 9,03 2,47
9,38 56,97 9,80 2,47
10,85 65,31 11,32 2,45
12,30 73,36 12,80 2,44
10,61 82,10 12,49 2,78
19,24 178,95 24,97 3,05
29,68 263,82 38,04 2,98
17,20 198,17 24,77 3,39
28,89 422,23 47,06 3,82
33,37 481,76 54,17 3,80
37,77 538,56 61,09 3,78
27,33 512,29 50,32 4,33
32,49 602,49 59,66 4,31
43,08 908,38 84,66 4,59
31,43 774,24 66,19 4,96
49,07 1175,19 102,64 4,89
42,19 1316,62 100,41 5,59
47,10 1822,78 124,61 6,22
54,60 2097,00 144,17 6,20
76,54 2871,47 200,73 6,12
111,54 4019,60 288,57 6,00
60,38 2814,36 175,18 6,83
96,96 5764,87 318,76 7,71
119,71 7006,39 391,72 7,65
141,96 8176,52 462,11 7,59
уо - уо
х–х
Jxo max, iхo max, Jyo min, Wyo min,
см4
см
см4
см4
55,64 2,24 15,00 5,70
29,00 2,45 7,81
3,26
36,80 2,44 9,52
3,87
42,91 2,43 11,18 4,44
46,03 2,72 12,04 4,53
50,67 2,72 13,22 4,92
59,64 2,71 15,52 5,66
68,19 2,69 17,77 6,31
76,35 2,68 19,97 6,99
62,65 2,91 16,41 5,74
73,87 2,90 19,28 6,62
84,61 2,89 22,07 7,43
94,89 2,87 24,80 8,16
104,89 2,86 27,48 8,91
83,56 3,11 21,80 7,10
90,40 3,11 23,51 7,60
103,60 3,09 26,97 8,55
116,39 3,08 30,32 9,44
130,00 3,50 33,97 9,88
283,83 3,84 74,08 18,51
416,04 3,74 111,61 25,79
314,51 4,28 81,83 19,29
670,02 4,82 174,43 34,94
763,90 4,78 199,62 39,10
852,84 4,75 224,29 43,10
813,62 5,46 210,96 39,05
956,98 5,43 248,01 44,97
1442,60 5,79 374,17 61,96
1229,10 6,25 319,38 52,52
1865,73 6,17 484,64 75,92
2092,78 7,04 540,45 78,15
2896,16 7,84 749,40 98,68
3333,00 7,81 861,00 111,50
4560,42 7,72 1181,92 146,62
6351,05 7,55 1698,16 193,06
4470,15 8,60 1158,56 138,62
9159,73 9,72 2370,01 242,52
11125,5 9,64 2887,26 287,14
12964,7 9,56 3388,98 327,82
zо ,
iyo min, см2
см
1,16 1,85
1,25 1,69
1,25 1,74
1,24 1,78
1,39 1,88
1,39 1,90
1,38 1,94
1,37 1,99
1,37 2,02
1,49 2,02
1,48 2,06
1,47 2,10
1,47 2,15
1,46 2,18
1,59 2,17
1,58 2,19
1,58 2,23
1,57 2,27
1,79 2,43
1,96 2,83
1,94 3,06
2,18 3,00
2,46 3,53
2,45 3,61
2,44 3,68
2,78 3,82
2,76 3,90
2,95 4,27
3,19 4,30
3,14 4,55
3,58 4,89
3,99 5,37
3,97 5,46
3,93 5,70
3,89 6,07
4,38 5,91
4,94 6,91
4,91 7,11
4,89 7,31
27
Таблица 1.6. Обозначения условные графические в схемах.
Элементы кинематики. По ГОСТ 2.770—68
28
29
30